馈能阻尼系统中的能量收集装置理论研究

杨国松，谢　毅，孙洪鑫，王修勇

(湖南科技大学 土木工程学院，湘潭 411100)



馈能阻尼系统中的能量收集装置理论研究

杨国松，谢毅，孙洪鑫，王修勇

(湖南科技大学 土木工程学院，湘潭 411100)

通过设计一种土木阻尼结构能量收集装置，对系统模型进行了分析并建立了能量收集系统的力学理论数学模型，运用MATLAB进行了在不同的振幅、频率、外接电阻等工况下系统不同受力情况的模拟分析,将系统的各个参数运用到MATLAB/simulink仿真中，进行电机的实时仿真，得出电机转速、电压、电磁矩等变化情况，建立了转速与各参数之间的关系.

能量收集;力学模型;MATLAB/simulink;永磁电机

0　引言

振动能量在自然界中广泛存在,振动式微型发电机可以通过拾振装置将外部的振动能量转换成电能,为无线传感器节点或低功耗微型电子设备供电.从20世纪末开始,机械、电气、材料等领域的很多研究人员展开了对振动式微型发电机[1-4]的探索研究.土木工程结构在强风、地震、波浪等外部激励下，容易产生大幅振动，如果把此类耗能元件替换成具有能量收集功能的换能器，主结构的振动能量能够很好地转化为电能.利用收集的能量可以实现土木工程结构的健康监测设备(如无线传感器网络结点)等提供电源，在土木工程领域具有广阔的应用前景，也是基于环境振动的可再生能源利用.

1　能量收集系统设计

1.1能量收集系统的设计

在土木结构中，通常将阻尼器用来结构的减振控制中，阻尼器在进行减振的过程中所消耗的机械能基本被浪费掉，本文通过设计一种在阻尼减振时的直线运动过程将其消耗的机械能进行回收的能量收集装置.该结构主要包括芯杆、自润滑装置、螺母、滚珠丝杆、电机.其结构构造简图如图1所示，图2为未加电机的系统装置.

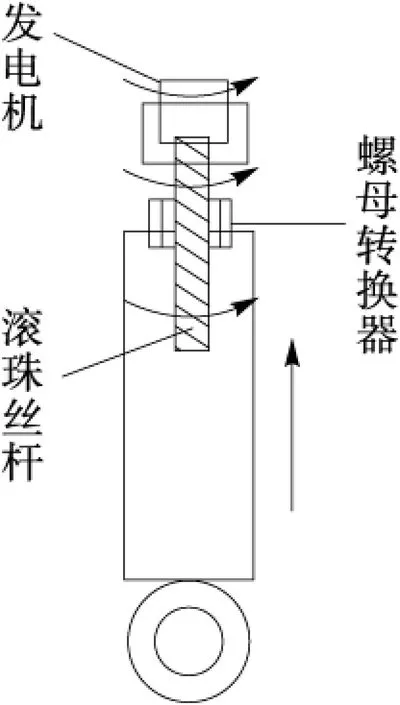
图1　能量收集系统结构简图

图2　能量系统实物图(未加电机)

1.2能量收集系统的工作原理

本新型能量收集系统的原理为：当系统处于减振的同时，丝杆导程杆随外部激励振动，从而引起滚珠丝杆螺母装置将结构振动由直线运动转化为旋转运动，经过传动装置带动电机的转子转动，随着转子的转动，线圈中的磁通量将发生改变，从而在线圈中产生感生电动势.同时电机的三相输出端接三相电器，在结构发生一定振动时，能够使电机能够得到较好的发电效率.

2　能量收集系统数学模型的建立

2.1系统结构的力学模型

(1)

(2)

其中a为传动效率.整个系统的力矩可以分为三个部分：滚珠丝杆产生的力矩，电机转动力矩，电机所产生的反电动势力矩.由我们所熟悉的转矩公式可以推导出滚珠丝杆及电机的转矩公式.

(3)

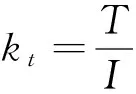
其中K—电枢槽数，N1—绕组元件匝数，β—极弧系数，D—电枢外径，L—电枢铁心长度， Bb—气隙密度.同时大量的实验和理论分析证明滚珠丝杆在转动的过程中会受到电阻尼力的影响，(电阻尼力与反电势力是等效的两个量)阻尼力的大小与电机本身的绕组和外接电阻有关[6].

(4)

其中：R为电机内部绕组;Rl为电机外接电阻值.

等效ce替代为随电阻接入的不同而产生的电机粘性阻尼，所以经过上述的转矩我们可以推出推动滚珠丝杆和电机旋转时所需要的轴向力，包括三个方面，滚珠丝杆，电机及电机所产生的电阻尼力.

(5)

其中η=0.94为滚珠丝杆的旋转效率，滚珠丝杆旋转效率采用姜洪奎博士论文数据[7].

系统整个的轴向力为各个部分力的组合(式9)，同时建立了整个系统的转矩方程(式7).

F=Ng+Nd+fe=

(6)

T=Tg+Tf+Td=

(7)

2.2各参数与系统轴向力之间的关系

通过模拟空载、外接不同的载路电阻、不同的激励振幅、振动频率值来测试系统的力学性能，外部的激励给予一个正弦波的形式，形式如：正弦激励波函数为:x=Asin(2πft)，来分析系统受力与各个因素之间的关系，具体的加载的参数及方法如表1所示.

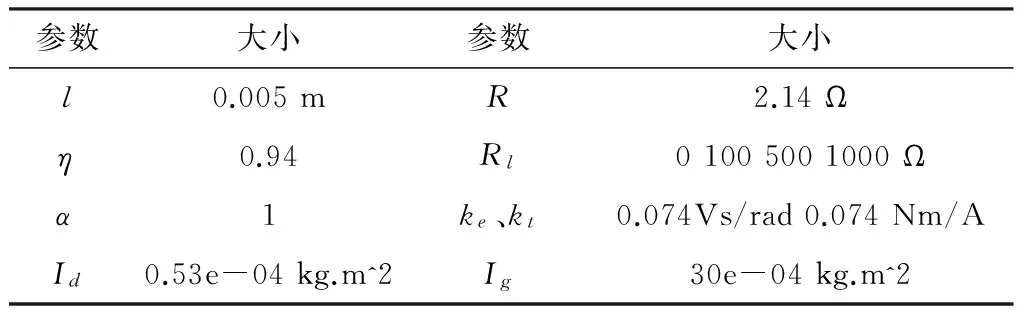
表1　加载的参数

2.3不同激励振幅、频率对系统受力的影响

图3是以表1中的实验参数下，空载情况下得到的不同激励和频率下对系统的轴向受力情况，图3(a)在频率为0.1 Hz，振幅A取了三个不同的数值，2.5 cm、7.5 cm、 10 cm，图3(b)在振幅为2.5 cm,频率取了三个不同的数值0.1 Hz、0.5 Hz、1 Hz.进行对比分析对系统所受轴向力的影响,从图3振幅与力的关系图、频率与力的关系图中可以看出，随着振动幅值、振动频率的增大，系统所受到的轴向力也随之增大.并且在振幅和频率之间可以较明显的看到频率对作用力的影响更为明显.

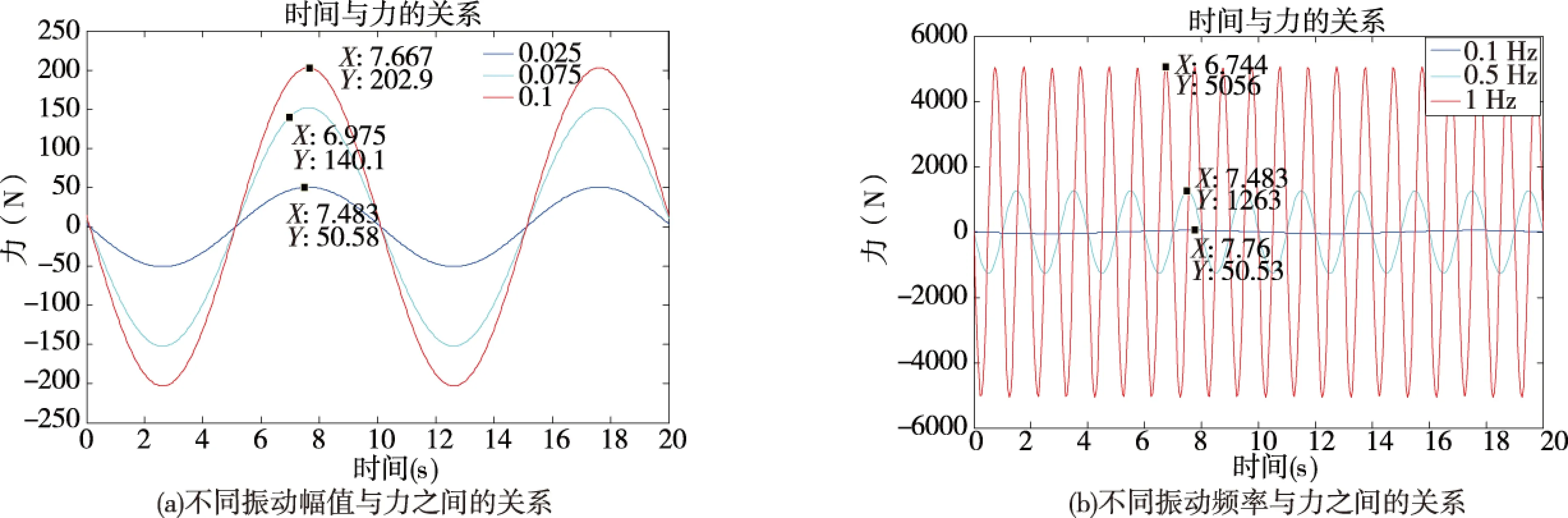
图3　幅值、频率对系统作用力的影响

2.4外接电阻及反电动势常数对系统所受到的电阻尼力的影响

图4(a)是以不同的外接电阻值Rl,来分析外接电阻对电机所产生的电阻尼力的影响，由图可以看出，在外接电阻值取三个不同的值，100 Ω、500 Ω、1000 Ω.实际所产生的电阻尼力都很小，我们可以推断在电机内部的反电动势常数ke确定之后，外接电阻值大小的改变对电阻尼力的影响不大，同时我们从图4(b)中发现，在空载情况下，不同的反电动势常数ke对系统电阻尼力产生影响很大,所以ke是影响电阻尼力的关键因素.

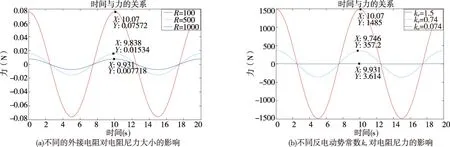
图4　外接电阻、反电势常数ke对电阻尼力的影响

3　仿真结果与分析

3.1系统的基本模块建立

通过matlab/simulink建立了图5中的电机基本模块、坐标变换模块、基本电压电流模块及图6中最终系统的仿真模型.

图5　基本电磁变换模型

图6　转矩方程及系统仿真图

3.2仿真结果

在前述系统力学方程的基础上，及表1中相关的参数的选择(外接三相电阻值为100 Ω)，搭建simulink仿真模型，取振幅A=0.025 m，频率f=0.1,通过式(7)转矩传递方程、示波器及相应的测量工具，当模型搭建完成之后(见图6b)，开始进行系统的加载方式中各种参数的设定，运行完成后对结果进行分析.

①在外加转矩的作用下，电机的转速，电流都有一个趋于稳定的阶段，当电机过渡到稳定阶段之后，电机的最终速度稳定在40～45 rad/s之间(见图7)，同时由图8可知d、q轴电压变化情况与转速变化情况类似，在一个急剧上升之后到达平稳状态.q轴电压稳定值接近2 V左右.图9中可以看到电机的电磁矩一直为负值，因为电机在默认状态下都是电动状态所以当电机作为电动机使用时电磁矩Te为推动力矩，为正值，当电机作为发电机使用时，Te为负值，阻碍转子旋转，达到稳定阶段之后，Te值在-1.5e-3左右.

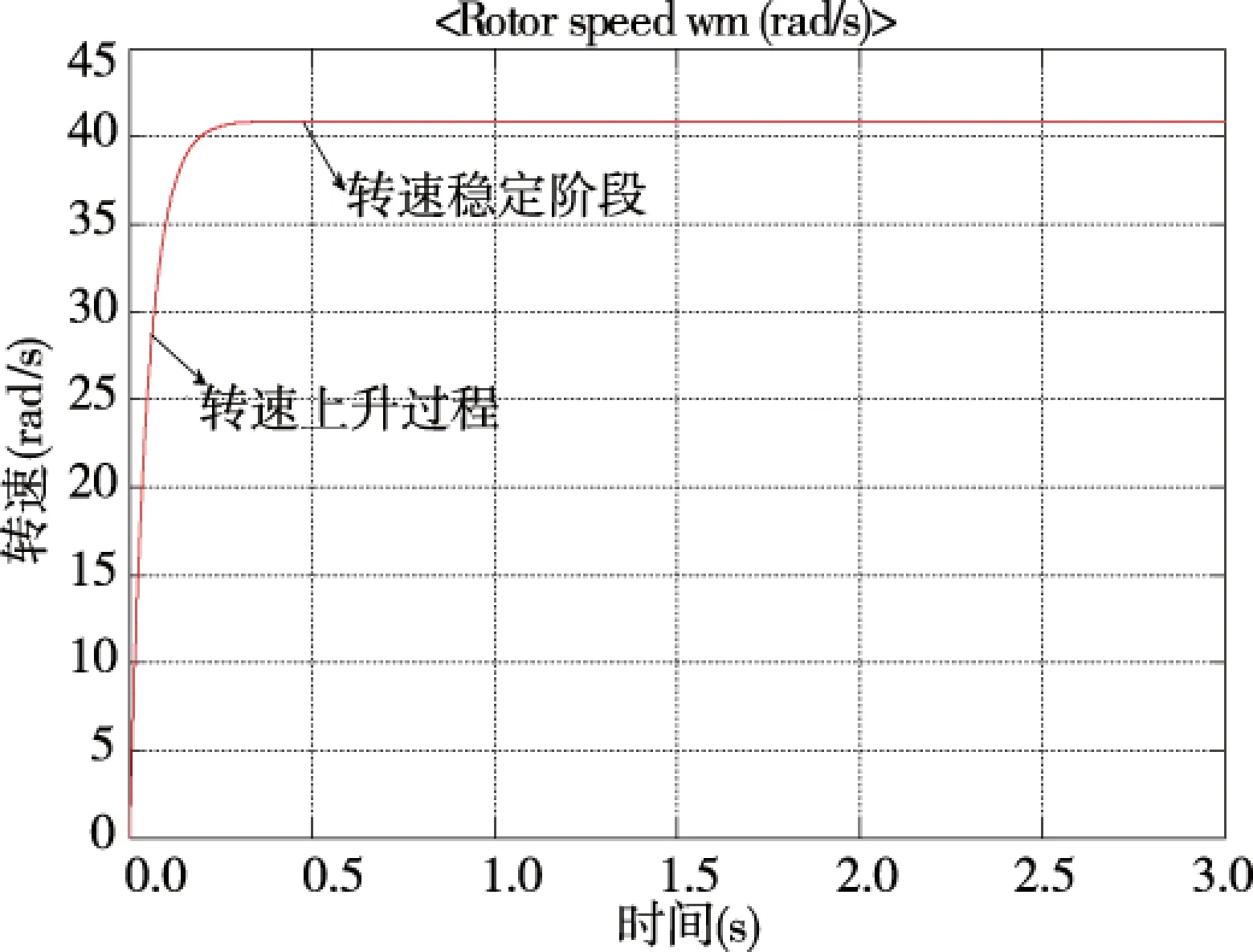
图7　转速随时间由上升过程到达稳定状态

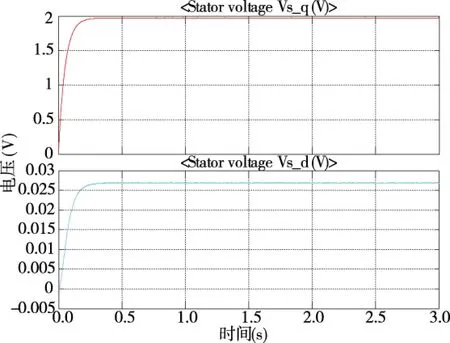
图8　q、d轴电压随时间变换曲线

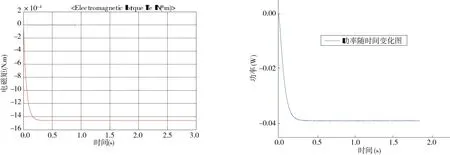
图9　电磁矩及功率随时间变化图

②三相电流随时间的变化(如图10(a)所示)电流为标准的简谐波形式，经过park[8]变换之后，三相电流投影到平面dq0轴上,如图10(b)所示，转速与电压、功率、电磁矩之间存在一定的关系，电压与转速之间的关系如图11所示，电流、电压与转速之间的关系符合永磁同步电机的变化规律[9]，同时与正弦波永磁电机所描叙的变化规律一致电压与转速之间的关系如图11(a)所示，通过origin9.1.6进行拟合，我们可以得到该系统电压与转速、电流与转速、转速与电磁矩之间的关系.

电压与转速间的关系式:

V=-0.028+0.048*w

为方便观测图形，我们取电磁矩与功率的绝对值进行作图，从图12(a)、图12(b)可以看出转速与电压、电磁矩之间的关系图皆符合电磁学基本关系，在没有达到额定转速之前，转速与电压、电磁矩之间呈线性相关.在达到额定转速之后，电压、电磁矩不在随转速上升，并且转速超过额定转速之后继续增加转速对电机本身有损伤.

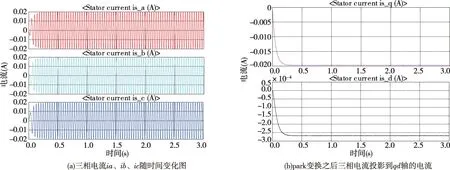
图10　三相电流及park变换后的dq轴电流

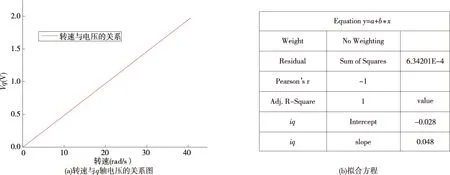
图11　转速与电压的关系

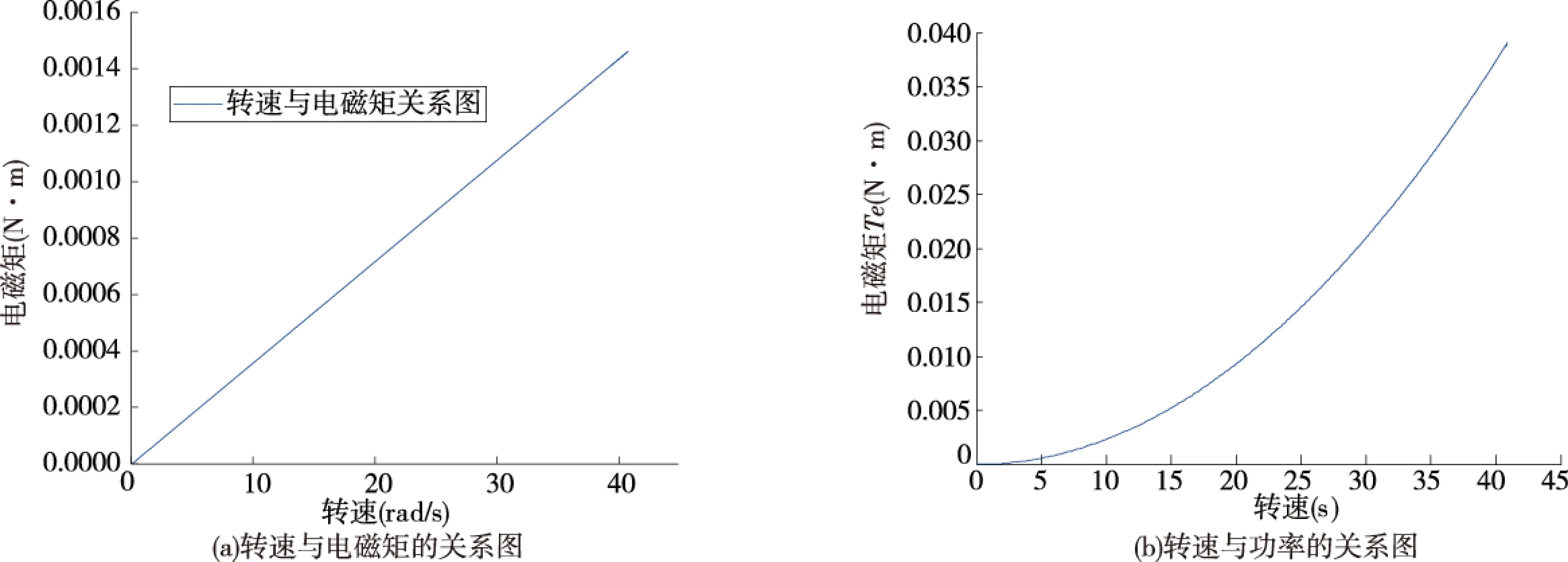
图12　转速与电磁矩、功率的关系

4　结论

本文设计了该新型能量收集系统的模型，同时推导出了系统的力学传动模型，对该类型的能量收集转速能够提供理论支持.在MATLAB/simulink的仿真下，证明该能量收集系统的方式可行，并且在频率和振幅都较小的情况下，三相电流、转速、电磁矩都处于比较理想的状态.符合永磁同步电机运行情况，并且找出了各参数之间的关系，比如转速与电压、电磁矩、功率的关系.对收集土木结构振动的可再生能源利用具有重要的参考意义.

[1] RoundyS,WrightPK,Rabaeyj.A Study of Low Level Vibration.as a Power Source for Wireless Sensor Nodes[J]. Computer Communication 2003,26:1131-1141.

[2] Mitcheson P D.Green TC Yeatman EM.etal.Architectures for Vibration Driven Micropower Generators [J] IEEE J. Microelectomech Syst， 2004， 13： 429-440.

[3] Beeby SP TudorM J White N M.Energy Harvesting Vibration Sources for Microsystems Applications[J].Measciteichnol,2006,17:175-195.

[4] Stephen N J On Energy Harvesting From Ambient Vibration [J]. Joumal of Sound and Vibration 2006， 293 :409-425.

[5] 张文海,谭宏松.永磁直流力矩电机设计计算中的反电势系数公式[J].电世界,2008,49(10):41-42.

[6] 邱家俊,塔娜.电机的电磁阻尼理论与转子的非线性振动[J].振动工程学报,2000,13(3):332-339.

[7] 陈希有,陈学允.基于PARK变换的空间矢量调制矩阵变换器的暂态分析[J].中国电机工程学报,2000,20(5):80-84.

[8] 刘杰.正弦波永磁同步电机电动及发电状态控制[D].中国科学院电工研究所硕士学位议论，2010:10-21.

Theoretical Study on Energy Harvesting in Fed Energy Damping System

YANG Guo-song,XIE Yi,SUN Hong-xin,WANG Xiu-yong

(College of Civil Engineering, Hunan University of Science and Technology， Xiangtan 411100, China)

Through designing a new type of structure energy collecting device, the system model and the theoretical model of energy harvesting system are established. The simulation analysis of the system under different amplitude, frequency, and external resistance is carried out by using MATLAB. By the simulation of the motor, the relationship between the motor speed, voltage, electromagnetic torque, and the parameters are established.

energy harvesting; Mechanics model; matlab; PMSM

2015-01-07

湖南省研究生科研创新项目(CX2015B504).

杨国松(1992—),男，硕士研究生，研究方向：结构振动控制、智能阻尼技术.

TP391.41

A

1671-119X(2016)03-0006-06