柔度曲率法在输电塔损伤识别中的应用

吴秀峰，常　青

（辽宁工程技术大学 建筑工程学院，辽宁 阜新 123000）



柔度曲率法在输电塔损伤识别中的应用

吴秀峰，常青

（辽宁工程技术大学 建筑工程学院，辽宁 阜新 123000）

在结构指纹识别方法中，基于柔度法的损伤识别方法能够较好地识别损伤所在位置及程度，在柔度法的基础上构建柔度曲率损伤识别指标及柔度矩阵曲率差损伤识别指标，并将其引入到输电塔结构损伤识别中。由于输电铁塔具有三个平动分量，所构建的两种损伤识别指标也具有三个方向分量，其在输电塔上的识别效果需要进一步分析。建立51 m酒杯型输电塔模型，分别采用两种指标对结构不同程度的单损伤及多损伤进行识别。研究结果表明，仅结构垂直方向分量的损伤识别指标能够识别结构损伤，但柔度曲率对于小损伤位置无法识别；柔度矩阵曲率差对小损伤位置也能较好地进行识别。

振动与波；酒杯型输电塔；柔度曲率；柔度曲率差；损伤识别；模态分析

输电塔结构作为我国的生命线工程，随着经济持续高速的发展与“西电东送”工程的大力实施，其高度、跨度与电压等级也都在稳定增长，因此，输电塔结构的可靠性直接关系到国民经济是否能稳定发展。在实际生活中，输电塔结构会受到风、雨、地震等环境荷载的影响，使结构在所难免地出现损伤，当损伤累积到一定程度后，在较大环境激励下则会发生倒塌事故，不仅会对经济的发展产生影响，而且影响到人民的日常生活。虽然国内外很多学者对输电塔进行了大量的研究［1-2］，但是现阶段对结构响应特征的复杂性认识仍不够全面，现有的防灾减灾措施很难应用到输电塔结构上来。

随着计算机技术及信号处理技术的迅速发展，结构健康监测技术（SHM）由于能够无损、实时地反映结构的动力特性，已被越来越多地应用到大型土木工程中来，其中，模态识别与损伤检测方法作为健康监测的核心，开始被国内外众多学者研究。

在结构损伤检测方法中，频率与振型由于能够直接由测试得到，而且识别精度较高，很多学者对此进行了大量的研究［3-6］，但结构损伤频率变化只能说明损伤存在而无法识别损伤的具体位置，振型识别指标又存在较大误差，很难满足工程实际需要。在基于频率与振型的损伤检测基础上，更多的损伤识别方法被提了出来，应用较多的如柔度法［7-8］、曲率法［9］、模态应变法［10］等。其中，采用柔度法利用结构损伤进行识别，具有较好的灵敏度，而且仅需要低阶模态就可以近似构建柔度矩阵，克服了实际工程中高阶模态难以识别的缺点。在此基础上，将柔度曲率法与柔度矩阵曲率差法应用到输电塔结构上来，建立柔度曲率与柔度曲率差损伤识别指标进行对比分析。但输电铁塔结构复杂，属于空间格构式结构，存在三个平动分量，在损伤分析时，根据三个振型分量构建的损伤识别指标的识别效果需要进一步分析。

建立51 m酒杯型输电塔模型，分析输电塔结构不同的损伤工况及不同方向分量所构建的柔度曲率损伤识别指标与柔度曲率差损伤识别指标的识别效果，为输电塔结构损伤识别提供依据。

1　理论基础

基于柔度的损伤识别方法由Pandey和Biswas提出［11］。定义结构的柔度矩阵

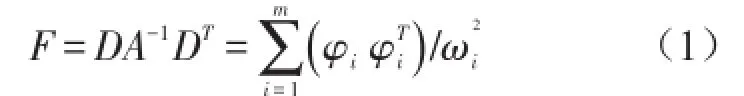
式中D为结构的正则化振型矩阵，m为测得结构前m阶固有频率，A=diag，ωi为结构第i阶固有频率，φi为结构第i阶质量归一化振型，F为柔度矩阵。

1.1柔度曲率法

根据式（1）可求得结构损伤后的柔度矩阵为Fd，取 fj为Fh第 j列所有值之和，即

式中 fij为Fh中的元素，由于结构节点与柔度矩阵列是一一对应的，因此，当结构某位置出现损伤时，结构的柔度会出现显著变化，这种变化可以通过 fj的变化来判断。而这种变化通过对 fj求其曲率CFh，将会更加明显

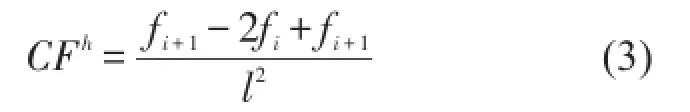
式中 fi+1、fi、fi-1分别表示三个相邻的节点，l为相邻两节点间距离，如果距离相等，可以忽略。

1.2柔度曲率差

根据式（1）求得结构损伤前后的柔度矩阵Fq、Fh，再分别求得曲率矩阵CFq、CFh，即

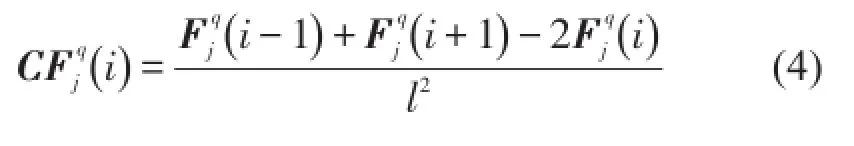
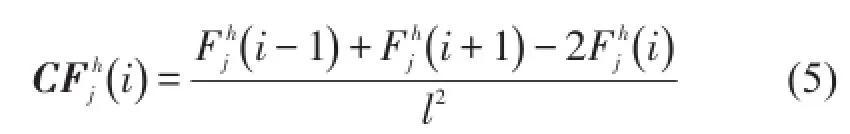
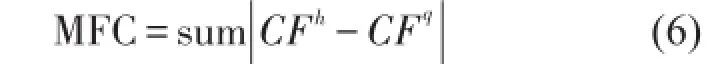
2　酒杯型输电塔结构模态分析

文中以辽宁地区酒杯型输电塔结构为原型，考虑导地线对输电塔频率的影响，运用集中质量点法将导地线质量与绝缘子质量附加在悬挂点处，运用Ansys建立梁桁式51 m输电塔有限元模型，档距400 m（如图1），结构的损伤假定为仅考虑结构单元弹性模量EI的降低而不考虑损伤单元质量的变化（结构损伤工况如表1）。表1中，a表示损伤程度。

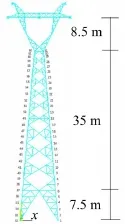
图1　51 m输电塔有限元模型

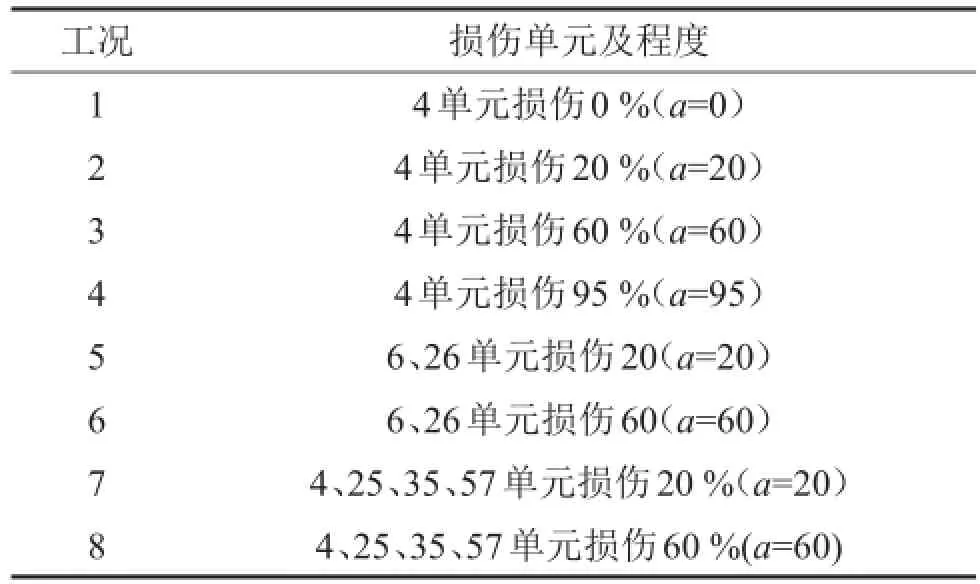
表1　结构损伤工况表

如图1所示，将输电塔结构所在平面分量定义为x、y方向分量，垂直方向分量定义为z方向分量。由式（1）可构建输电铁塔柔度矩阵

根据式（7），结构损伤识别指标FC与MFC也分为三个方向分量。

3　输电塔结构单损伤分析

结构模型如图1所示，数字表示节点编号，两个节点为一个单元，单损伤时FC考虑工况1到工况4，MFC考虑工况2到工况4，两个指标的损伤识别效果如图2、图3所示。

通过图2、图3可以看出，两种损伤识别指标值随着损伤程度的增加成幂指数增加，结构损伤程度达到95%时，损伤程度为20%的识别曲线由于突变值太小而被遮盖，根据这种递增关系可以对损伤程度进行定量分析。可以看出，x与z方向分量曲线存在太多突变点，无法识别结构损伤所在。在损伤较大时，可以确定两种损伤识别指标y方向分量识别损伤所在突变位置与所设立损伤工况一致。提取结构y方向分量20%损伤程度下两种指标识别曲线如图4所示，柔度曲率虽然在损伤处存在突变，但无损处也存在较大程度的突变，出现了误判。而柔度曲率差突变位置与损伤工况一致，无损处没有突变，表现出了较好的识别效果。

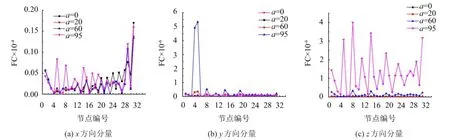
图2　结构第4单元不同损伤程度下柔度曲率值

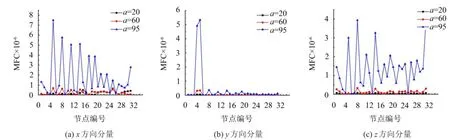
图3　结构第4单元不同损伤程度下柔度曲率差值

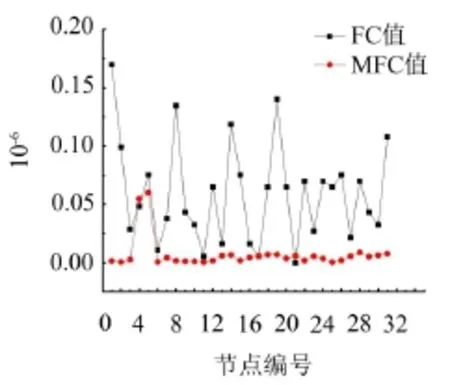
图4　结构第4单元损伤20%时FC与MFC值

4　输电塔结构多损伤分析

从单损伤识别结果可以看出，只有y方向的损伤识别指标能够较好地识别出结构损伤所在位置，在多损伤时，仅考虑两种指标在y方向分量上的识别效果。在单损伤工况下，两种识别指标对于大损伤均表现出较好的识别效果，多损伤时，不考虑95%损伤工况。首先考虑结构单条主材存在两个单元损伤的情况，考虑工况5和工况6情况下，FC和MFC两个指标的损伤识别情况，如图5所示，可以看出，当结构损伤较小时，FC指标出现多个峰值，无法判断小突变处是否为损伤单元，识别效果不佳；当损伤程度较高时，可以发现第6、第26号单元处指标值较大，但无损处仍然有较大突变值影响识别效果；而MFC指标能够很好地识别20%损伤下的多单元损伤，而无损单元的MFC值基本趋近于零，具有很好的识别效果。

由于输电塔由四根主材组成，考虑输电塔不同主材发生损伤情况下，对称位置损伤对FC和MFC指标损伤识别是否存在影响。选取x对称方向的两条塔腿，考虑工况7和工况8情况下两种指标的识别情况如图6所示，从MFC图可以看到，结构第31、第32节点间单元MFC值很大，然而此单元并不存在。第31号节点为一条主材塔身顶部节点号，第32号节点为另一条主材塔腿底部第一个节点号，两节点柔度差值很大，这种差值会对FC指标产生干扰，因此在FC图中，将两点柔度曲率做归零处理。可以看出，FC识别指标对小损伤工况识别效果不好，大损伤工况下突变节点较多，但损伤处FC值最大，能够识别大损伤的损伤位置；MFC值没有对第31号节点与第32号节点做处理，也能看出，对于小的损伤，识别效果较好，对称位置的损伤也能够识别出来。

5　结语

文中对结构损伤识别较好的柔度曲率法和柔度矩阵曲率差法引入到输电塔损伤识别当中，发现两种指标仅y方向分量才能识别结构的损伤及程度；对于输电塔结构不同主材对称位置的损伤，两种识别指标均有较好的识别效果。其中，柔度曲率法不需要结构损伤前的柔度矩阵，故更容易应用在实际工程中，但对于小损伤不能有效识别；当损伤程度较高时，对于单损伤及多损伤都可以较好地识别出来；柔度矩阵曲率差法需要损伤前后的柔度矩阵，但损伤识别效果比柔度曲率法要好，能够识别不同损伤工况下的损伤。

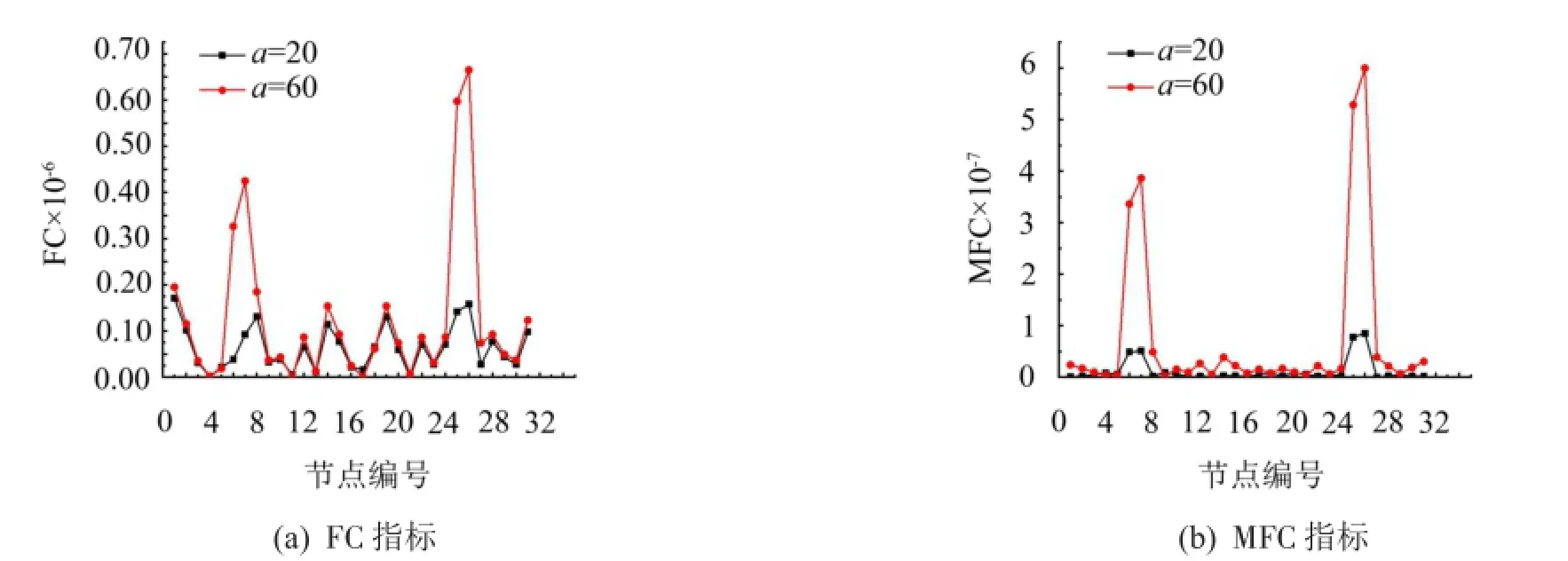
图5　结构第4单元、第26单元不同损伤程度FC、MFC值

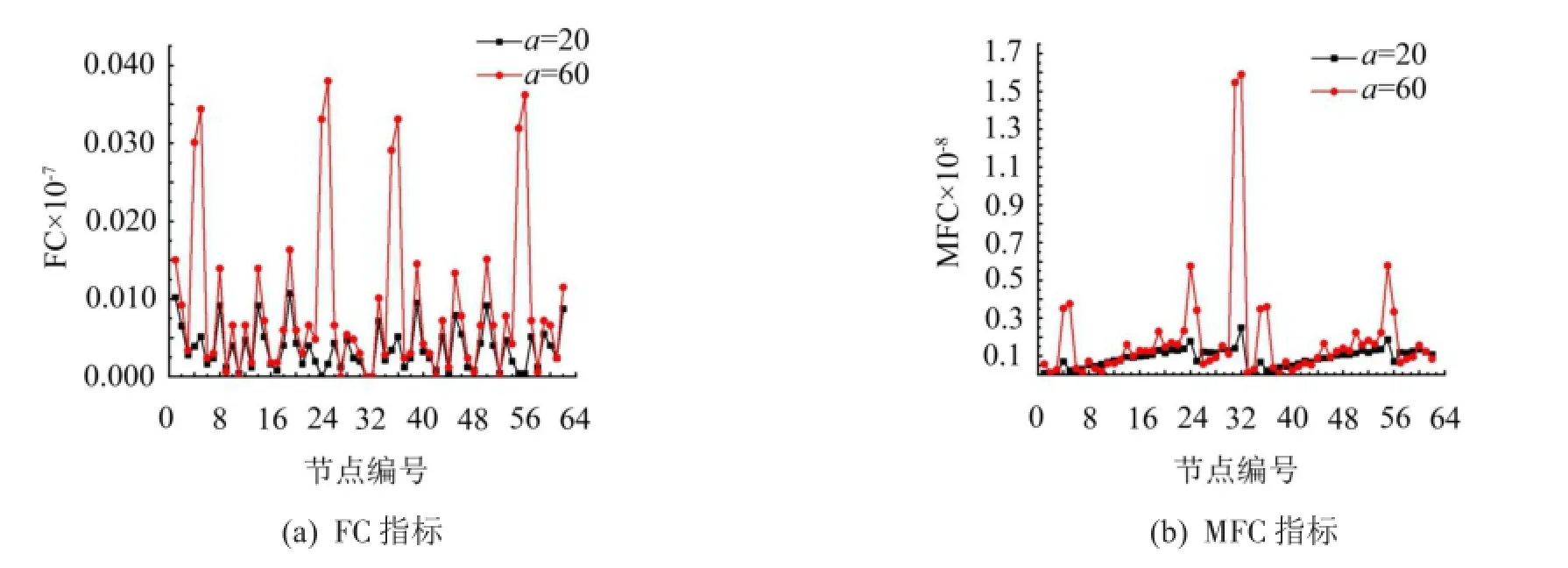
图6　结构第4、第25、第35、第57单元不同损伤程度FC、MFC值

［1］李宏男，白海峰.高压输电塔-线体系抗灾研究的现状与发展趋势［J］.土木工程学报，2007，40（2）：39-46.

［2］汪江，杜晓峰，田万钧，等.500 kV淮蚌线淮河大跨越输电塔振动测试与模态识别［J］.中国电力，2009，42（2）：30-33.

［3］ADAMS R D，CAWLEY P，PYE，STONE.A vibration technique for non-destructively Assessing the integrity of sturctuers［J］.JournalofMechanicalEngineering，Science，1978，20（2）:93-100.

［4］HEARN G，TESTA R B.Modal analysis for damage detectioninstructures［J］.JournalofStructural Egnineering，ASCE，1991，117（10）:3042-3061.

［5］KHIEM N T，LIEN T V.Multi-crack detection for beam by the natural frequencies［J］.Journal of Sound and Vibration，2004，237（1）:175-184.

［6］韩东颖，时培明.基于频率和当量损伤系数的井架钢结构损伤识别［J］.工程力学，2011，28（9）：109-114.

［7］ZHAO J，DEWOLF J T.Sensitivity study for vibrational parameters used in damage detection［J］.Journal of Structual Engineering，1999，125:410-416.

［8］曹晖，张新亮，李英民.利用模态柔度曲率差识别框架的损伤［J］.振动与冲击，2007，26（6）：116-124.

［9］PANDEY A K，BIWASM，SANMAN M M.Damage detection from changes in curvature mode shapes［J］. Journal of Sound and Vibration，1991，145:321-332.

［10］郭惠勇，薛晓武，李正良，等.采用应变能方法定量分析输电塔损伤程度［J］.重庆大学学报，2012，35（12）：94-99.

［11］PANDEY A K，BISWAS M.Damage detection in structures using changes in flexibility［J］.Journal of Sound and Vibration，1994，169:3-17.

Application of Flexibility Curvature Method in Damage Detection of Transmission Towers

WU Xiu-feng，CHANGQing

（Institute ofArchitecture and Civil Engineering，Liaoning University of Engineering Technology，Fuxin 123000，Liaoning China）

The fingerprint identification and damage identification methods based on flexibility method can be used to identify the damage location and intensity.In this paper，the flexibility curvature damage identification index and flexibility curvature difference matrix damage identification index are built based on the method of flexibility.These indexes are introduced to the damage identification of transmission tower structures.Since the transmission tower has three translational motion components and each of the two damage identification indexes also has three direction components，the recognition effect of the damage in the transmission tower needs further analysis.So，a model of 51 meter-high glass-shaped transmission tower is established，the two indexes are used to identify the single damage and multi damage of the tower structures.The results show that only using the flexibility matrix of the vertical component of the structure can identify the structure damage.Both indexes have good effect，but the flexibility curvature method is unlikely to recognize the location of small damage.While the flexibility curvature difference matrix method can identify the location of the small damages

vibration and wave；glass-shaped transmission tower；flexibility curvature；flexibility curvature difference；damage identification；modal analysis

TP206+.3

ADOI编码：10.3969/j.issn.1006-1335.2016.04.037

1006-1355（2016）04-0174-04+205

2016-02-01

辽宁省一般项目资助（L2015222）

吴秀峰（1976-），男，辽宁省阜新市人，博士，副教授，主要从事钢结构、大跨度空间结构等方向的研究。E-mail:wxf19760825@163.com