形态分量分析和谱峭度在轴承故障诊断中的应用

马朝永，张学飞，胥永刚

（北京工业大学 机电学院先进制造技术北京市重点实验室，北京 100124）



形态分量分析和谱峭度在轴承故障诊断中的应用

马朝永，张学飞，胥永刚

（北京工业大学 机电学院先进制造技术北京市重点实验室，北京 100124）

滚动轴承发生故障时，其振动信号往往包含多种振动分量，主要由轴承自身固有振动引起的谐振分量、点蚀或裂纹等故障产生的冲击分量和其他的干扰分量组成。实现故障信号中各分量的有效分离非常有利于轴承的故障诊断。针对此问题，提出形态分量分析和谱峭度相结合的故障诊断方法，首先用形态分量分析处理轴承故障信号，使信号中的冲击分量与谐振分量分离，再以谐振分量为对象，利用谱峭度方法对谐振分量进行滤波，对滤波结果进行Hilbert包络解调分析，然后根据包络谱诊断滚动轴承发生的故障。实验结果表明，这种方法可以提取到明显的故障特征频率，从而验证了该方法的有效性。

振动与波；滚动轴承；故障诊断；形态分量分析；谱峭度

滚动轴承作为机械设备中最常用的零部件之一，它的运行状态直接影响到整台设备的性能，许多机械设备发生故障都与滚动轴承有关［1］，因此，对滚动轴承故障诊断方法的研究具有十分重要的意义。滚动轴承发生局部损伤时，其振动信号往往主要由轴承自身固有振动引起的谐振分量、点蚀或裂纹等故障产生的冲击分量和其他的干扰分量组成，实现信号中各分量的分离，对故障诊断有非常重要的作用。

2004年，Starck等学者基于信号的稀疏表示和形态多样性，提出了形态分量分析（Morphological Component Analysis，MCA）的信号处理方法［2］，该方法首先用于图像处理［3］和脑电波信号分离［4］，取得了良好效果。最近，一些学者将MCA用于齿轮和轴承的复合故障诊断中［5-6］，取得了一定效果。MCA的主要思想是根据信号中不同组成成分之间的形态差异性，不同形态特征的信号分量可以用不同的稀疏字典表示，选取合适的稀疏表示字典，可以实现信号中不同形态特征分量的有效分离。

文中提出了一种基于MCA和快速谱峭度（Fast Spectral Kurtosis，FSK）［7-9］结合的故障诊断方法，首先利用MCA对轴承原始故障信号进行处理，将原始信号分解为一个冲击分量与一个谐振分量，然后以谐振分量为研究对象，对其进行FSK带通滤波，再对经FSK滤波处理后的信号进行包络解调，从包络谱中可以找到非常明显的故障特征频率。利用这种诊断方法处理轴承内圈故障的振动信号，结果表明，这种方法可以有效提取轴承内圈故障特征频率，验证了这种方法的有效性与可行性。

1　形态分量分析的基本原理

1.1MCA基本原理

假设待分析信号s由K个形态特征明显不同的分量线性叠加组成，每个形态分量都存在着能够对应稀疏表示该分量的字典，即sk=Φkαk，其中Φk为完备稀疏字典，αk为sk在字典中的分解系数。字典Φk仅能稀疏表示与之相对应的形态分量sk，对于其他分量则不能稀疏表示。信号s的稀疏分解可以归结为求解如下式所示的优化问题

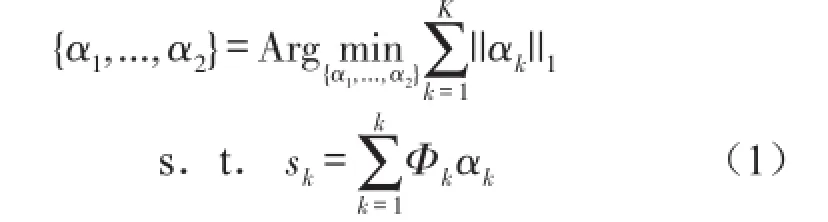
放宽式（1）的约束条件，可转化为

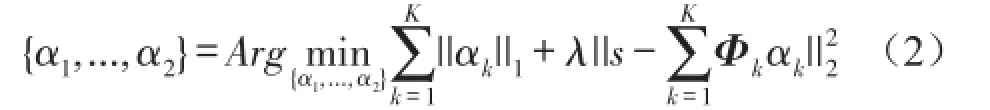
式中λ为给定阈值。

根据sk=Φkαk，给定sk，可得到αk

根据式（2）和式（3），可将式（1）中各变换系数｛α1，...，αk｝的优化问题转化为各形态分量｛s1，...，sk｝的优化问题

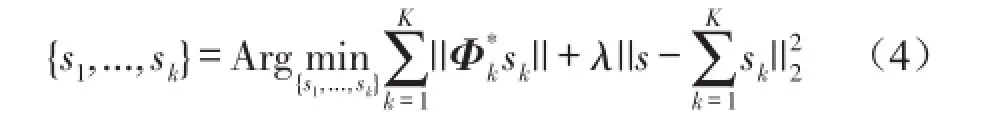
1.2MCA算法步骤

根据式（4）的优化问题，Starck等在BCR算法的基础上，给出了MCA算法的数值实现步骤。

（1）选取合适的字典Φk（k=1，2，...，K），初始化最大迭代次数Lmax，设置初始阈值δ=λ×Lmax；

（2）初始化各形态分量sk=0（k=1，2，...，K）；

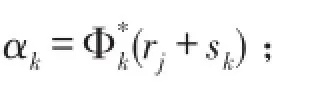
（5）采用软阈值方法对变换系数进行阈值更新，阈值为δ，得到更新的变换系数；

（7）更新阈值δ=δ-λ；

（8）如果δ≥λ，跳转到第三步继续循环计算，否则，跳出循环，计算结束。此时，可得到各形态分量sk（k=1，2，...，K）及残余分量r。

1.3MCA算法仿真

为验证MCA算法的分离效果，设置如式（5）所示的信号

式中s（t）由K个幅值为Ai、频率为 fi的正弦波信号叠加构成，表示信号中变化缓慢的谐振分量，表达式如式（6）所示

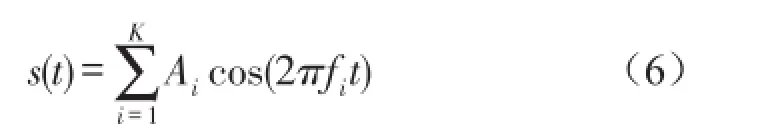
h（t）由M个幅值为Bm、衰减系数为β、共振频率为 fr的单脉冲信号构成，表示周期性的冲击分量，表达式为

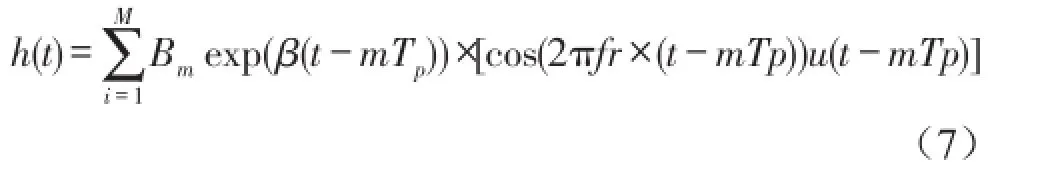
式中u（t）为单位阶跃函数。

取采样频率为1 024 Hz，采样点数为512个点，将表1中的各参数代入式（6）和式（7），得到的冲击信号和谐振信号如图1所示。

表1　仿真信号的各参数值

图1　仿真冲击信号和谐振信号

将式（6）和式（7）代入式（5）中，得到合成的仿真信号，如图2所示。

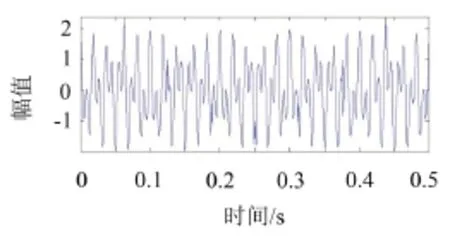
图2　仿真合成信号

对图2所示仿真的合成信号进行形态分量分析，可以得到两个形态分量，分别为图3中所示的冲击分量（上图）和谐振分量（下图）。比较图1和图3可以发现，在无噪声的情况下，MCA方法可以将混合信号中的冲击分量和谐振分量进行完美地分离。

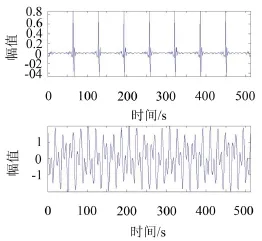
图3　MCA分离的冲击分量与谐振分量

2　谱峭度

谱峭度（Spectral Kurtosis，SK）首先由Dwyer提出，其主要思想是计算每根谱线的峭度值，从而发现隐藏非平稳的存在，并指出所在的频段。Antoni将谱峭度规范化，提出基于滤波频带的谱峭度快速算法。谱峭度定义为能量归一化的4阶谱累积量，用来度量一个过程在某一频率上的概率密度函数的峰值的大小。谱峭度对信号中瞬态成分敏感性很高，并可以精确地找到所对应的频率。因此，谱峭度可以检测信号中的瞬态成分。

信号x（t）的Wold-Cramer分解在频域的表达式为

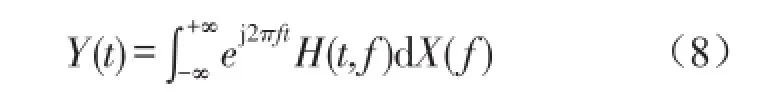
式中H（t，f）为Y（t）在f处的复包络函数。

过程Y（t）的4阶谱累计量定义为

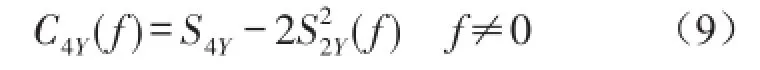
其中S（f）为谱瞬时矩，定义为

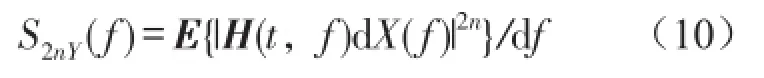
即可得到谱峭度的定义

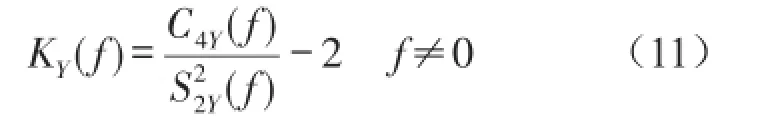
3　实验数据分析

实验系统如图4所示，由轴承实验台、压电式加速度传感器、数据采集仪、计算机组成。正常的和有故障的轴承分别安装在试验台上两个轴承座上，由数据采集仪将传感器采集到的振动信号保存到计算机上，进行数据处理分析。实验所用轴承型号为6307，内圈发生点蚀故障，电机转速为1 496 r/min，采样频率为15 360 Hz，经计算，该轴承的内圈故障特征频率为122.738 Hz。

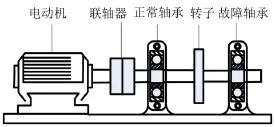
图4　轴承故障试验台

滚动轴承内圈故障振动信号的波形和频谱如图5所示，图中信号波形中包含较为明显的周期性冲击成分，但是频谱中包含很多频率成分，从中找不出故障特征频率。因此，选取DCT字典和8阶Symmlet小波字典组合，利用MCA方法对该信号进行处理，得到的冲击分量（上图）与谐振分量（下图）如图6所示。

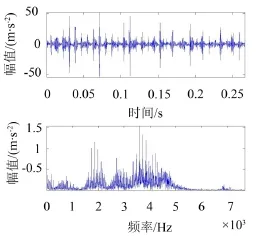
图5　内圈故障信号的时域波形和频谱

分别对上述所得的冲击分量与谐振分量作傅里叶变换，所得频谱如图7所示。

利用谱峭度方法对上述冲击分量与谐振分量进行快速谱峭度计算，图8和图10分别是冲击分量与谐振分量的快速谱峭度图，先看冲击分量，最大峭度值为38.7，在第0层，中心频率和带宽分别为3 840 Hz、7 680 Hz，按照这些参数对谐振分量进行带通滤波，然后对滤波后的结果作希尔伯特包络解调分析，包络谱如图9所示。

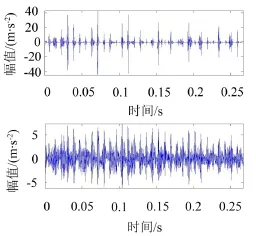
图6　内圈故障信号的MCA处理结果

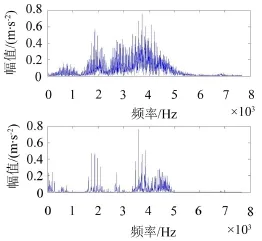
图7　冲击分量和谐振分量的频谱

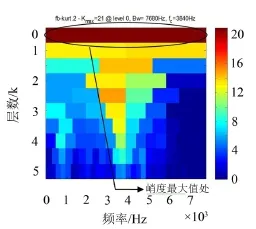
图8　冲击分量快速谱峭度图

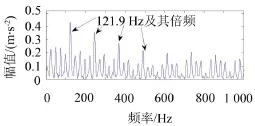
图9　最大谱峭度值滤波信号包络谱

从图9中可以找出频率121.9 Hz及其倍频成分，与故障特征频率122.738 Hz非常接近，但是同时也包含很多其他频率的干扰成分。再看谐振分量，最大峭度值为1.4，出现在第2.5层，带通滤波器中心频率为1 920 Hz，带宽为1 280 Hz，按照这些参数对谐振分量进行带通滤波，然后对滤波后的结果作希尔伯特包络解调分析，包络谱如图11所示。

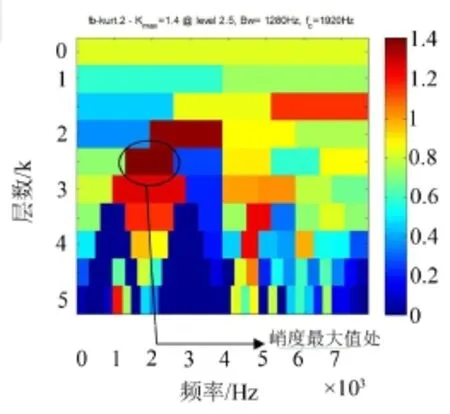
图10　谐振分量快速谱峭度图

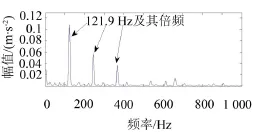
图11　最大谱峭度值滤波信号包络谱

从图11中可以明显找到轴承内圈故障特征频率121.9 Hz及其倍频成分，而且基本看不到其他频率的干扰成分。

从以上的结果来看，轴承故障振动信号经过MCA的处理，可以将周期性的故障冲击成分提取出来，但是提取出来的冲击分量中，发生脉冲的部位夹杂着许多干扰成分，由于这些干扰的存在，削弱了周期性冲击成分的能量，使得冲击分量的频谱频带变宽，而边频带较谐振分量的频谱并不明显。因为冲击分量中存在明显的冲击现象，所以在整个频带上的峭度值最大，即冲击分量经FSK分析后是在整个频带上做带通滤波，再进行Hilbert包络解调，这样不能去除夹杂在其中的干扰成分，最后的效果并不理想。而轴承故障振动信号经过MCA处理，并不能够将冲击分量与谐振分量完全分离开，因此再对谐振分量做同样的处理，最终得到的包络谱中含有很少的干扰成分，而故障特征频率非常明显，效果要比用冲击分量好很多。

图12为直接对谐振分量所作的希尔伯特包络谱图，图中虽然包含轴承内圈故障特征频率121.9 Hz及其倍频成分，但是同时也包含很多其他的频率干扰成分，效果不佳。

为了说明谱峭度方法的优越性，对上面MCA得到的谐振分量进行传统带通滤波处理，然后再进行希尔伯特包络解调分析。分别以1 000 Hz、2 000Hz、3 000 Hz、4 000 Hz为中心频率构造带通滤波器进行分析，最终的包络谱分别如图13、图14、图15、图16所示。

图12内圈冲击分量的包络谱

图13中包含很多频率成分，难以找出明显的故障特征频率121.9 Hz。

图14中可以找出明显的故障特征频率121.9 Hz及其倍频，并且效果与谱峭度方法的效果几乎一样，仅在幅值上略有差异，原因是滤波器中心频率2 000 Hz与上面谱峭度方法所得出的中心频率1 920 Hz接近。图15中可以找出故障特征频率121.9 Hz，但同时包含其他频率成分，效果不佳。图16中包含很多频率成分，难以找出明显的故障特征频率121.9 Hz。

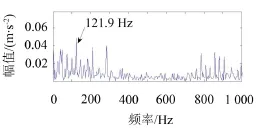
图13　中心频率为1 000 Hz的滤波信号包络谱

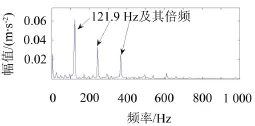
图14　中心频率为2 000 Hz的滤波信号包络谱

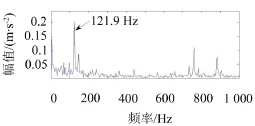
图15　中心频率为3 000 Hz的滤波信号包络谱

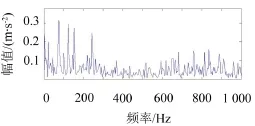
图16　中心频率为4 000 Hz的滤波信号包络谱

进行传统带通滤波时，不容易直接确定出合适的中心频率，不同的中心频率造成不同的滤波结果。由于谱峭度方法可以确定最佳带通滤波器参数，因此用谱峭度方法进行带通滤波时，效果要优于传统带通滤波。

4　结语

研究了将形态分量分析与谱峭度结合的故障诊断方法，用来处理实验中的轴承内圈故障振动信号，可以提取到明显的故障特征频率，实现轴承的故障诊断，验证了该方法的有效性。

（1）选取DCT字典和8阶Symmlet小波字典组合，利用MCA可以将信号中的冲击分量与谐振分量分离。

（2）根据谱峭度的快速峭度图可以自动确定带通滤波器的最佳带宽和频带中心。

（3）将MCA与谱峭度结合的方法应用于故障诊断中，可以有效和准确地提取故障特征，实现故障识别。

［1］胥永刚，孟志鹏，赵国亮等.双树复小波包和谱峭度在齿轮箱故障诊断中的应用［J］.北京工业大学学报，2014，40（4）：488-494.

［2］STARCK J L，MOUDDEN Y，BOBIN J.Morphological component analysis［C］.Proceedings of SPIE，2005，59（14）:1-15.

［3］STARCK J L，ELAD M，DONOHO D.Redundant multiscale transforms and their application for morphological component seperation［J］.Advances in Imaging and Electron Physics，2004，132（82）:287-384.

［4］YONG X Y，WARD R K，BIRCH G E.Generalized morphologicalcomponentanalysisforeegsource sepration and artifact removal［C］.Proceedings of the 4 th InternationalIEEEEMBSConferenceonNeural Engineering，Antalya，Turkey，2009:343-347.

［5］李辉，郑海起，唐力伟.基于改进形态分量分析的齿轮箱轴承多故障诊断研究［J］.振动与冲击，2012，31（12）：135-140.

［6］李辉，郑海起，唐力伟.形态分量分析在齿轮箱复合故障诊断中的应用［J］.振动、测试与诊断，2013，33（4）：620-626，724-725.

［7］ DWER R F.Detection of non-gaussian signals by frequencydomainkurtosisestimation［C］.Acoustic，Speech and Signal Processing.Boston:IEEE International Confference on ICASSP，1983:607-610.

［8］ANTONI J，RANDALL R B.The spectral kurtosis：a useful tool for characterizing non-stationary signals［J］. Mechanical Systems and Signal Processing，2006，20（2）:282-307.

［9］ ANTONI J，RANDALL R B.The spectral kurtosis：application to the vibratory surveillance and diagnostics of rotating machines［J］.Mechanical Systems and Signal Processing，2006，20（2）:308-331.

［10］陈向民，于德介，李蓉.基于形态分量分析与阶次跟踪的齿轮箱复合故障诊断方法［J］.航空动力学报，2014，29（1）：225-232.

［11］陈向民，于德介，李星，等.形态分量分析在转子早期碰摩故障诊断中的应用［J］.振动工程学报，2014，27（3）：466-472.

［12］李海山，吴国忱，印兴耀.形态分量分析在地震数据重建中的应用［J］.石油地球物理勘探，2012，47（2）：236-243.

Applications of Morphological ComponentAnalysis and Fast Spectral Kurtosis in Rolling Bearing Fault Diagnosis

MA Chao-yong，ZHANG Xue-fei，XU Yong-gang

（Key Laboratory ofAdvanced Manufacturing Technology of Beijing，College of Mechanical Engineering andApplied Electronics Technology，Beijing University of Technology，Beijing 100124，China）

When a rolling bearing is faulted，its vibration signal is usually composed of many components generated by different vibration sources.These components are dominated by the harmonic components induced by the natural vibration of the bearing，the impulsive components resulted from fitting or crack faults and some other perturbation components.It is helpful to separate these components from the original vibration signals effectively for fault diagnosis of the rolling bearing. In this paper，a new fault diagnosis method is proposed based on morphological component analysis（MCA）and fast spectral kurtosis（FSK）.Firstly，the impulsive components and harmonic components are separated from the vibration signals of the faulted rolling bearing by using MCA.Then，the harmonic components are analyzed by using FSK filtering analysis.Finally，the signals obtained from the previous steps are analyzed by using Hilbert envelope demodulation analysis.The fault diagnosis of a rolling bearing is carried out according to the envelope spectrum method.The feasibility and effectiveness of this method are verified by the experiments.

vibration and wave；rolling bearing；fault diagnosis；morphological component analysis；fast spectral kurtosis

TH133.3；TH165

ADOI编码：10.3969/j.issn.1006-1335.2016.04.036

1006-1355（2016）04-0169-05+197

2016-01-28

国家自然科学基金资助项目（51375020）；北京市教委科研计划资助项目（KM201310005013）

马朝永（1970-），男，河北省石家庄市人，博士，副教授，主要研究方向为汽车零部件检测、故障诊断。E-mail:machaoyong@bjut.edu.cn