车辆-轨道非线性耦合系统交叉迭代算法及应用

雷晓燕，吴神花，张　斌

（华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013）



车辆-轨道非线性耦合系统交叉迭代算法及应用

雷晓燕，吴神花，张斌

（华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013）

运用有限元法建立车辆-轨道非线性耦合系统振动分析模型，该模型包含车辆、轨道两个子系统，其中车辆子系统为附有二系弹簧的整车模型，轨道结构子系统为离散的三层弹性梁模型。两子系统通过轮轨非线性接触力和位移协调条件实现耦合。针对车辆-轨道非线性耦合系统动力学方程提出了交叉迭代算法。为加速迭代收敛速度，引入松弛法对轮轨接触力进行修正。为证明算法的正确性，进行了算例验证。同时还给出了CRH3高速动车在有砟轨道上运行时引起车辆和轨道振动的实例，分析中考虑了轮轨线性和非线性接触及不同列车速度对车辆和轨道结构振动的影响。计算结果表明交叉迭代算法具有程序编制简单、收敛速度快、用时少、精度高的优点；采用轮轨线性接触模型得到的车辆和轨道结构的动力响应比轮轨非线性接触模型得到的结果要大，其中位移、加速度最大值和振幅增大范围约在15%以内，轮轨接触力最大值和振幅增大范围约在5%以内。

振动与波；车辆-轨道非线性耦合；交叉迭代算法；轮轨非线性接触；轮轨线性接触；松弛法

随着客运高速化、货运重载化和运输密度的大幅提高，车辆与轨道系统动力学问题更加突出，也日趋复杂。车辆-轨道动力学理论研究也越来越深入，并取得了一系列的成果。例如翟婉明教授建立车辆-轨道耦合动力学统一模型［1］，并提出两种新型数值积分方法［2］；向俊、曾庆元运用矩阵的“对号入座”法则建立车辆-轨道系统运动方程［3］；张格明等建立车辆、有碴轨道和无碴轨道、简支箱梁桥垂向和横向耦合系统动力分析模型，系统分析我国铁路干线主要形式的轨道不平顺对中高速车辆走行性能的影响，得到了一般规律性的结论［4］；宣言等建立了高速铁路曲线线路车线耦合系统有限元模型，对曲线线路在高速行车条件下的耦合系统动力学性能进行仿真［5］。雷晓燕、张斌等建立列车-轨道-路基耦合系统动力分析模型，提出车辆单元和轨道单元的概念［6］；冯青松、雷晓燕等为了分析不平顺条件下高速铁路轨道结构振动，推导移动车辆在轮对处和轨道结构在轮轨接触点处的柔度矩阵，建立了移动车辆-轨道垂向耦合振动的解析模型［7］。夏禾、曹艳梅等利用解析的波数-频域法建立列车-轨道-大地耦合模型［8］。冯牧、雷晓燕对列车引发建筑物振动及隔振进行试验与数值分析［9］。涂勤明和雷晓燕等研究地铁产生的环境振动及轨道结构减振技术措施［10］。以上研究各有特色，但主要是针对车辆-轨道线性耦合系统动力学问题，而对轮轨之间非线性接触算法以及由此引起的车辆和轨道结构非线性动力响应分析很少涉及。文中运用有限元法建立车辆-轨道非线性耦合系统振动分析模型，该模型包含车辆、轨道两个子系统，其中车辆子系统为附有二系弹簧、阻尼的整车模型，下部轨道结构子系统为离散的三层弹性梁模型，两子系统通过轮轨非线性接触力和位移协调条件实现耦合。针对车辆-轨道非线性耦合系统动力学方程，提出了交叉迭代算法。为加速迭代收敛速度，引入松弛法对轮轨接触力进行修正。为证明算法的正确性，进行了算例验证。同时还给出了CRH3高速动车在有砟轨道上运行时引起车辆和轨道振动的实例，分析中考虑了轮轨线性和非线性接触及不同列车速度对车辆和轨道结构振动的影响。计算结果表明文中提出的交叉迭代算法具有程序编制简单、收敛速度快、用时少、精度高的优点。

1　基本假设

在用有限元法建立车辆-轨道非线性耦合系统竖向振动模型时，采用以下基本假设：

（1）仅考虑车辆-轨道耦合系统竖向振动效应。

（2）车辆系统和轨道-路基系统沿线路方向左右对称，可取一半结构研究。

（3）上部车辆系统为附有二系弹簧阻尼的整车模型，车体和转向架考虑沉浮振动和点头振动。

（4）轮轨间为非线性弹性接触。

（5）钢轨被离散为二维梁单元，轨下垫板和扣件的弹性及阻尼分别用弹性系数ky1和阻尼系数cy1表示。

（6）轨枕质量作为集中质量处理并仅考虑竖向振动效应；枕下道床的支承弹性系数和阻尼系数分别用ky2和cy2表示。

（7）道砟质量简化为集中质量并仅考虑竖向振动效应；道砟下路基的支承弹性系数和阻尼系数分别用ky3和Cy3表示。

2　车辆子系统

车辆子系统为附有二系弹簧阻尼的整车模型，如图1所示。

图1　上部车辆子系统模型

运用Lagrange方程，可得到上部车辆子系统的动力学方程为

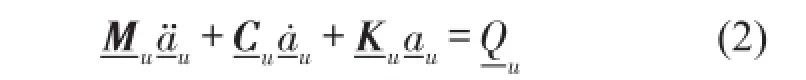
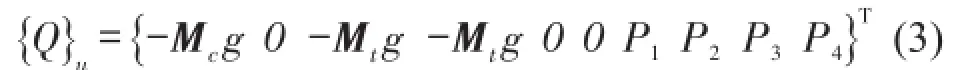
图中Mc、Jc为1/2的车体质量与转动惯量；Mt、Jt为1/2转向架质量与转动惯量；ks1、ks2为车辆一、二系悬挂刚度；cs1、cs2为车辆一、二系悬挂阻尼；Mwi（i=1，2，3，4）为第i个车轮的质量；vc、φc为车体沉浮振动的竖向位移、车体点头振动的角位移；vti、φti（i=1，2）为前、后转向架沉浮振动的竖向位移、点头振动的角位移；vwi（i=1，2，3，4）为第i个车轮的竖向位移。考虑轨面随机不平顺，不平顺幅值用η表示，与四个车轮接触处的不平顺幅值分别为η1、η2、η3、η4。

定义车辆单元节点位移向量

Pi=-Mwig+Fuli，Fuli为第i个车轮的轮轨触力，可根据轮轨相对接触竖向位移由赫兹公式求得。

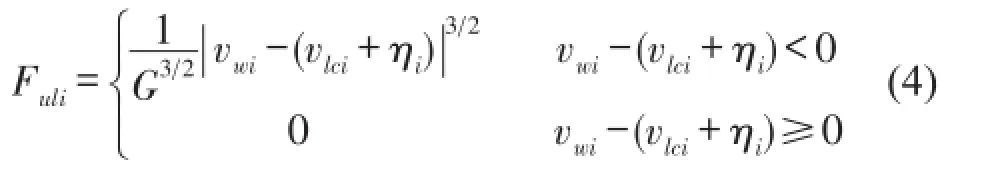
其中vwi、vlci分别为车轮、钢轨在第i个轮轨接触处的位移，ηi为钢轨表面不平顺，G为接触挠度系数［11］。

3　有砟轨道子系统

有砟轨道子系统模型如图2所示。

图2有砟轨道子系统模型

图3为有砟轨道单元模型，图中v1、v4表示钢轨的竖向位移；θ1、θ4表示钢轨的转角；v2、v5表示轨枕的竖向位移；v3、v6为道砟的竖向位移；mt、mb分别为四分之一的轨枕质量和两轨枕间道砟质量；l为有砟轨道轨枕间距。

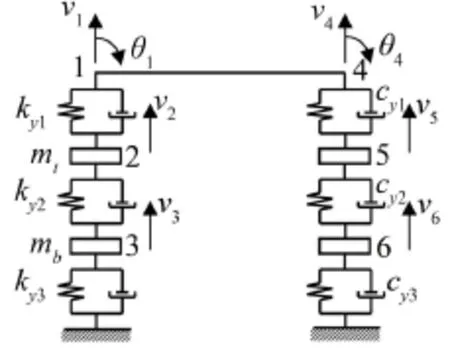
图3　有砟轨道单元模型

定义有砟轨道单元的结点位移为

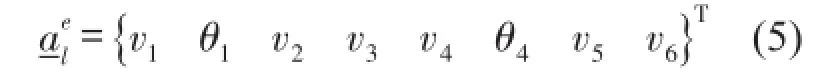
运用有限元法，可得到下部有砟轨道子系统的有限元方程为

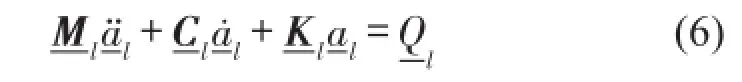
4　交叉迭代算法

采用Newmark数值积分法求解车辆-轨道非线性耦合系统动力学方程，下面给出了用交叉迭代算法求解车辆-轨道非线性耦合系统动力学方程的步骤。

在车辆和轨道两子系统中要求解的方程为二阶常微分方程组。

对于车辆结构，见图1，式（2）可改写为

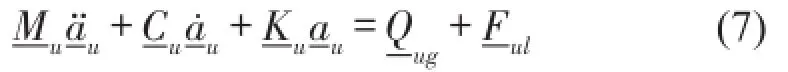
若将Hertz非线性刚度线性化，则有

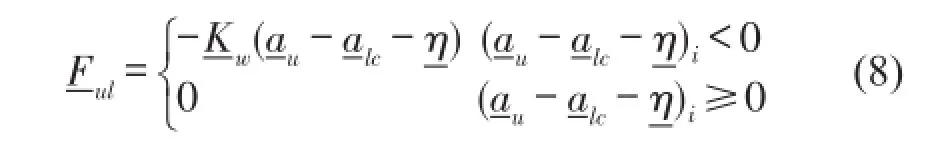
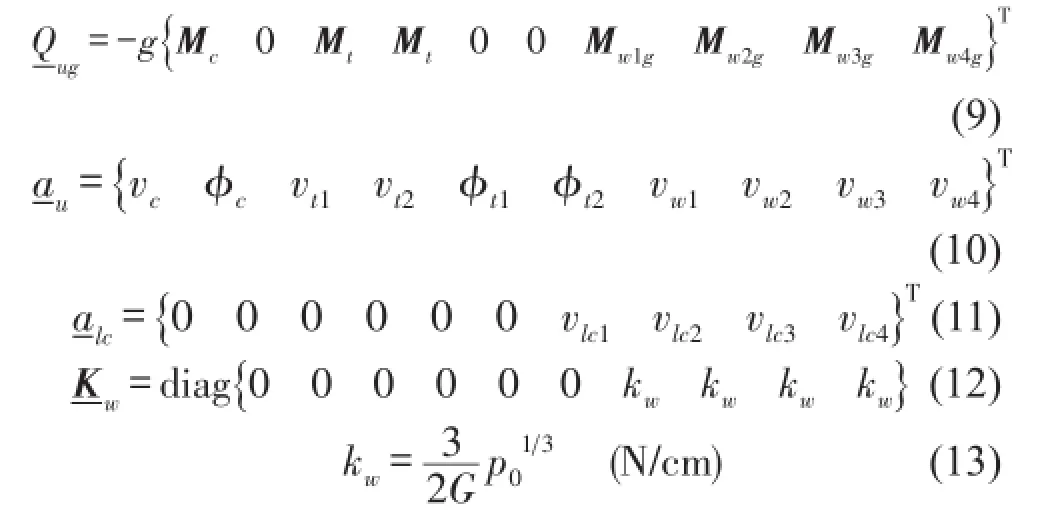
kw为轮轨线性化接触刚度，p0为车轮静荷载。式（7）经刚度线性化后还可写成

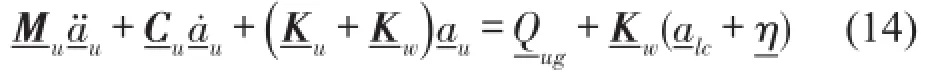
对于轨道结构，如图2所示，式（6）可写成

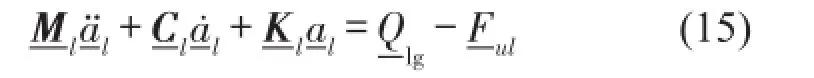
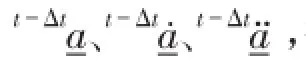
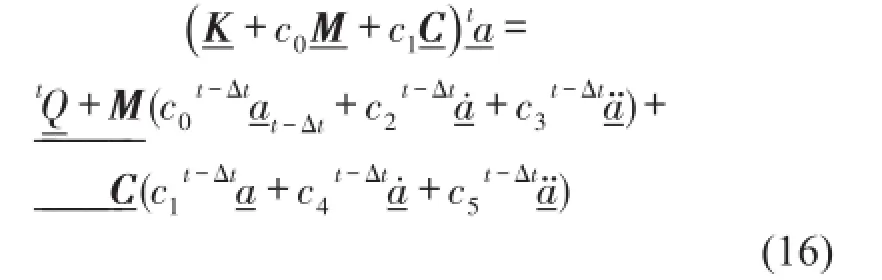
其中ci（i=0，1，2，...，7）为Newmark算法系数［12］。

现给出主要计算步骤如下：

1）初始计算

（1）在起始第一时间步和首次迭代时，假设轨道结构初始位移通常可取=），根据可得到第i个轮轨接触处的初始钢轨位移i=1，2，3，4），进而得到。

2）对时间步长循环

设在时间步长t，已进行了k-1次迭代，现考察第k次迭代：

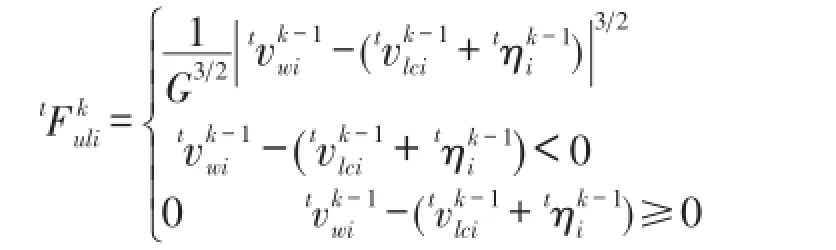
（2）运用松弛法对轮轨接触力进行修正，令

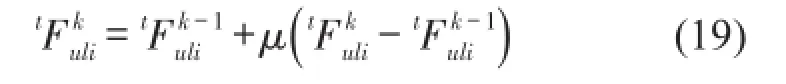
其中μ为松弛因子，一般取0＜μ＜1，根据时间步长选取μ的值，如时间步长为0.001 s时μ=0.3时可获得很好的效果。

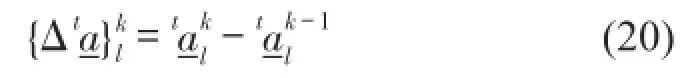
定义收敛准则为

（6）计算轨道位移差值

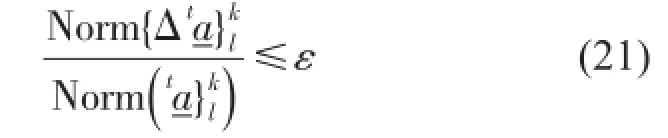
其中

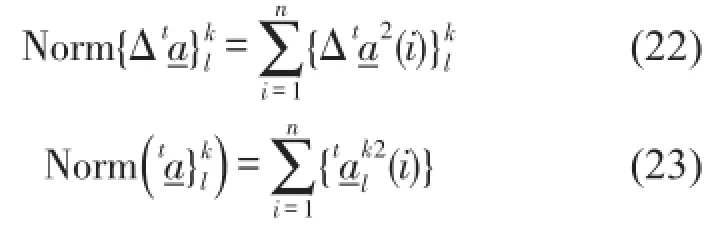
ε取1.0×10-8～1.0×10-5之间的数。

（7）对轨道位移进行收敛性判别。

① 如果收敛性得到满足，转步骤II，进入下一时间步长循环，令t=t+Δt，并取

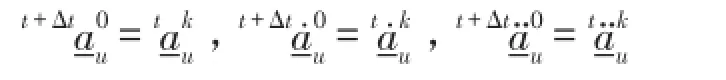
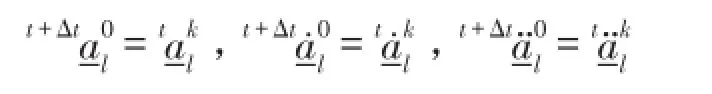
继续计算，直至整个计算时域T。

② 如果收敛性不满足，转步骤II，令k=k+1，进入下一迭代步循环。

5　模型验证

为了验证模型和方法的正确性，采用文中提出的交叉迭代算法计算文献［7］中的算例。分别用两种方法分析整车通过时车辆和轨道的动态响应，其中车辆为我国高速铁道车辆，轨道为60 kg/m有砟轨道，列车速度为252 km/h，假设轨道为完全平顺，其它参数见文献［7］。参考文献计算结果见图4（a），本文计算结果见图4（b），可见两者吻合良好。

6　车辆-轨道非线性耦合系统动力响应分析

若不引入松弛因子，则算法对时间步长选取要求较高。当时间步长超过某一限值时，迭代不收敛；当时间步长选取过大时，即使引入松弛因子算法仍不收敛。当算法收敛时，时间步长、松弛因子越大，收敛速度越快，程序运行时间越短。但时间步长过大时，松弛因子须取较小数值才能保证算法收敛。所以为提高算法收敛速度，需要综合考虑时间步长和松弛因子的影响。对一般工程问题，当时间步长取为0.001 s，且松弛因子 μ=0.3时可获得很好的效果。

作为车辆-轨道非线性耦合系统动力响应分析的实例，考虑高速整车CRH3通过时车辆和轨道结构的动力响应，列车参数见表文献［13］，轨道结构为60 kg/m有砟轨道，无缝线路，其参数见参考文献［14］。采用美国六级不平顺功率谱密度函数作为轨道不平顺的激励。分别考虑轮轨线性和非线性接触以及不同列车速度（V=80 km/h、120 km/h、160 km/ h、200 km/h）对车辆和轨道结构振动的影响。取轨道长度为200 m，时间积分步长取为0.001 s。

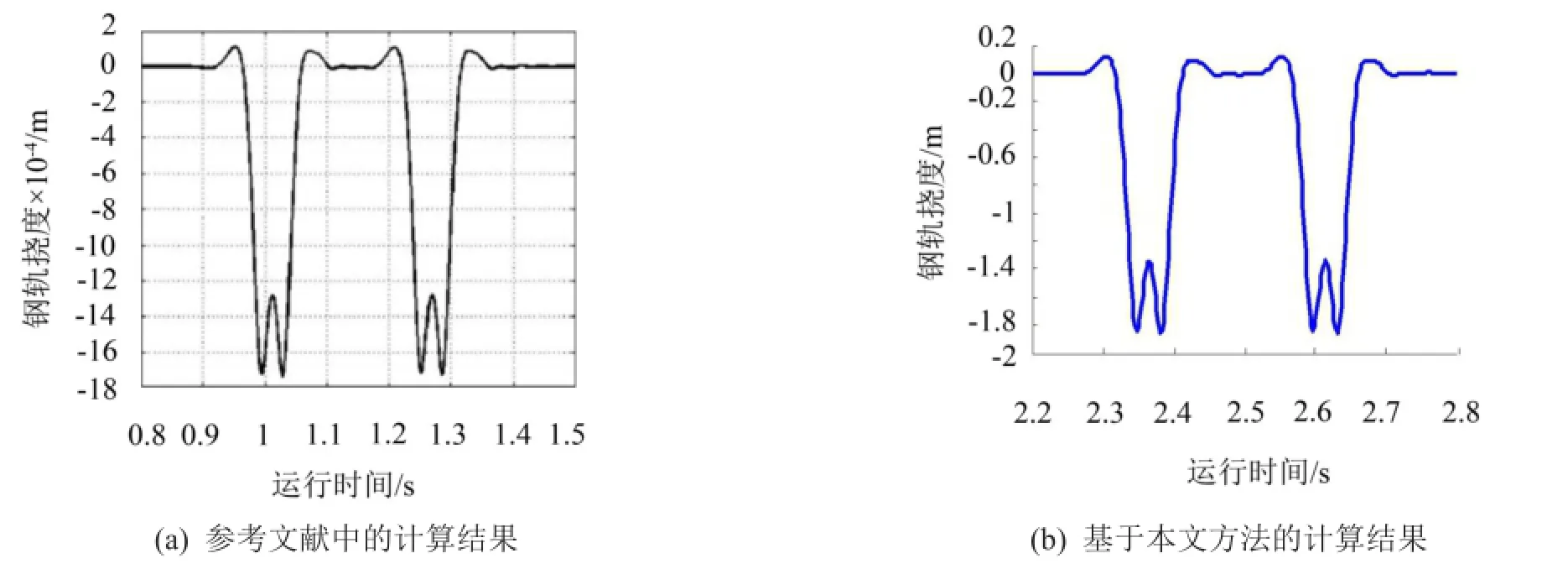
图4　钢轨挠度曲线

计算结果见表1至表10，它们分别代表考虑轨道不平顺激励和不同列车速度工况下，轮轨线性接触和非线性接触所对应的钢轨位移、轨枕位移和道床位移、钢轨加速度、轨枕加速度和道床加速度、车轮加速度、转向架加速度和车体加速度以及轮轨接触力的最大值和振幅。

从表1至表3可见在线性接触时速度对轨道结构位移影响较大，当列车速度从80 km/h增加到200 km/h，在线性接触时钢轨、轨枕、道床的振幅分别从1.15 mm、0.745 mm、0.556 mm增加到1.38 mm、0.96 mm、0.729 mm，增幅为20%、28.8%、31.1%。在非线性接触时，道床位移振幅随速度增大而增大，钢轨、轨枕位移振幅在速度为200 km/h时最大，在速度为160 km/h时和120 km/h时的结果接近相等，但在速度为80 km/h时比速度为160 km/h时的结果大。

钢轨、轨枕和道床最大竖向挠度和振幅在线性接触时比非线性接触时大，其增大范围在15%以内。

从表4至表6可见钢轨、轨枕和道床加速度最大值和振幅也增加随着速度的增加而增大，在线性接触时其振幅从速度为80 km/h时的115.8 m/s2、41.4 m/s2、33.4 m/s2增加到速度为200 km/h时的515.4 m/ s2、108 m/s2、121 m/s2，增幅分别为345.1%、160.9%、 262.3%，非线性接触时其振幅增加的幅度分别为349.8%、172.8%、258.2%。

线性接触时钢轨、轨枕和道床加速度最大值和振幅比非线性接触时大，其增大范围在10%以内。

从表7至表9可以看出：转向架和车体的加速度振幅随着速度的增加而增加，线性接触时其加速度从速度为80 km/h时的8.27 m/s2、0.451 m/s2增加到11.70 m/s2、0.784 m/s2，增幅分别为41.5%、73.8%；非线性接触时增幅分别为50.6%、51.1%。而车轮加速度随着速度的增加基本增大，但是车轮的加速度振幅在车速为80 km/h时比120 km/h时大，这可能与轨道个别点不平顺幅值过大有关。

考虑轮轨线性接触时的转向架和车轮的加速度振幅比非线性接触时略大，其增大范围在5%以内；车体加速度振幅在200 km/h时线性接触比非线性接触时略大，其它速度下则基本相等，但无论是最大值还是振幅都在1 m/s2范围内，说明车辆的一、二系弹簧阻尼系统具有良好的隔振作用。

从表10可以看出：轮轨力最大值和振幅基本随速度增加而增大，但速度为80 km/h时的轮轨力最大值和振幅比120 km/h时的略大些；当速度从120 km/ h增加到200 km/h，线性接触时轮轨力最大值和振幅分别从97.3 kN、51.9 kN增加到112 kN、84.2 kN，增幅为15.1%、62.2%；非线性接触时轮轨力最大值和振幅分别从93.4 kN、51.3 kN增加到113 kN、86.6 kN，增幅为20.9%、68.8%。

表1　钢轨位移最大值和振幅

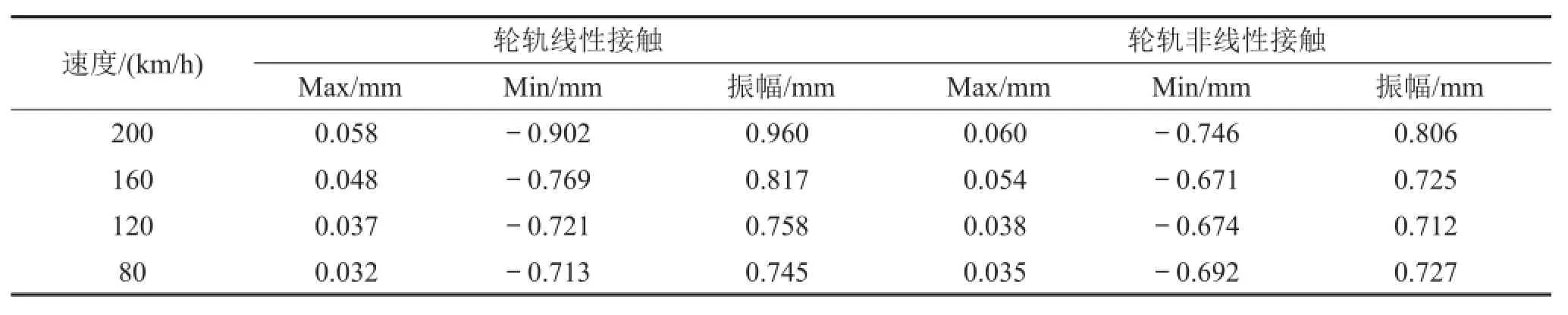
表2　轨枕位移最大值和振幅

表3　道床位移最大值和振幅

轮轨力最大值在线性接触时比非线性时略大些，轮轨力振幅差别较小。

7　结语

文中运用有限元法建立了车辆-轨道非线性耦合系统振动分析模型，该模型包含车辆、轨道两个子系统，其中车辆子系统为附有二系弹簧、阻尼的整车模型，轨道结构子系统为离散的三层弹性梁模型，两子系统通过轮轨非线性接触力和位移协调条件实现耦合。针对车辆-轨道非线性耦合系统动力学方程，提出了交叉迭代算法。为加速迭代收敛速度，引入了松弛法对轮轨接触力进行修正。通过对车辆-轨道非线性耦合系统动力响应的实例分析，得到下列结论：

（1）采用交叉迭代算法和引入松弛因子对轮轨接触力进行修正能加快算法收敛速度，在每一时步中只要经过3～8次迭代即可收敛。

（2）将车辆-轨道非线性耦合系统分解为车辆子系统和轨道子系统，可分别独立求解，既降低了分析问题的规模，又减小了程序设计的难度。同时，由于两个子系统有限元方程的系数矩阵全部为定值，且为对称矩阵，只须对方程的系数矩阵一次求逆，在每一时步的迭代中只须进行回代计算，因而极大地提高了计算速度。目前已有的基于“对号入座”求解车辆-轨道耦合系统动力响应的算法，随着车辆在轨道上的位置不断改变，有限元耦合方程的系数矩阵也在不断变化，因此在每一时步的计算中，需要进行求逆运算，大大降低了计算效率。通过对列车在200 m长轨道上运行引起车辆和轨道动力响应实例的仿真分析，得到结论：采用文中提出的“交叉迭代算法”在普通计算机工作站上运行用时只须5 min，而基于“对号入座”算法用时则需要60 min，一般情况下，前者的计算效率是后者的4～6倍，求解问题的规模越大则计算效率越高。

表4　钢轨加速度最大值和振幅

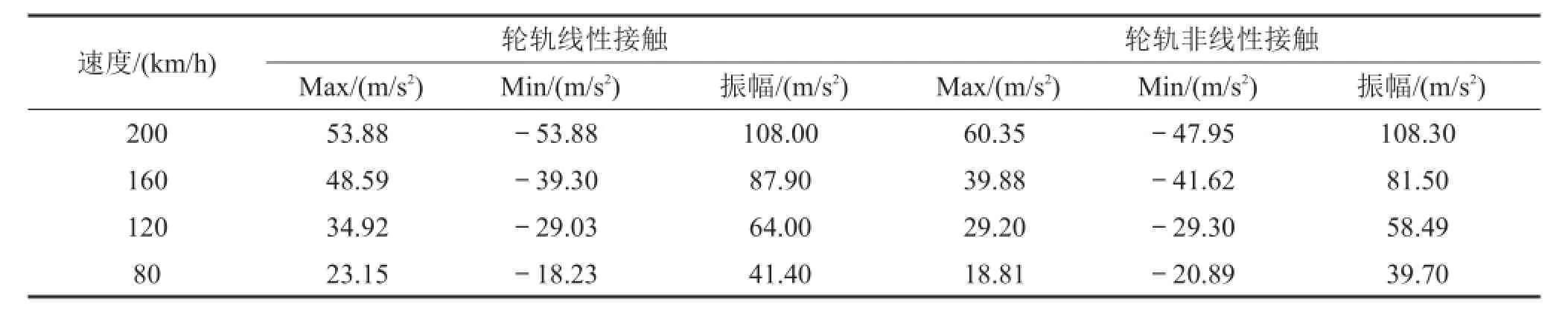
表5　轨枕加速度最大值和振幅

表6　道床加速度最大值和振幅

表7　车轮加速度最大值和振幅

表8　转向架加速度最大值和振幅

表9　车体加速度最大值和振幅

表10　轮轨接触力最大值和振幅

（3）列车速度对车辆和轨道结构的动力响应有显著影响，无论是轮轨线性接触模型还是非线性接触模型，钢轨、轨枕和道床的位移，钢轨、轨枕、道床、转向架和车体的加速度以及轮轨接触力均随着列车速度的提高而增加；采用轮轨线性接触模型得到的车辆和轨道结构的动力响应比轮轨非线性接触模型得到的结果要大，其中位移、加速度最大值和振幅增大范围约在15%以内，轮轨接触力最大值和振幅增大范围约在5%以内。因此，在按轮轨线性接触模型进行车辆、轨道结构振动分析，并根据分析结果进行结构设计是偏保守和偏安全的。

最后指出，文中提出的算法具有普遍适用性，可推广应用于移动荷载作用下的各类线性和非线性问题的分析中。

［1］翟婉明.车辆-轨道垂向系统的统一模型及其耦合动力学原理［J］.铁道学报，1992，14（3）：10-21.

［2］ZHAI W M.Two simple fast integration methods for largescale dynamic Problem in Engineering［J］.International Journal for Numerical Methods in Engineering，1996，39（24）:199-21.

3］向俊，曾庆元.关于机车车辆-轨道系统运动方程的建立［J］.长沙铁道学院学报，2000，8（4）：1-5.

［4］张格明，罗林.中高速条件下车线桥动力分析模型与轨道不平顺影响［J］.中国铁道科学，2001，22（4）：136-138.

［5］宣言，万家，王澜.高速铁路曲线线路车线耦合系统动力学性能仿真分析［J］.中国铁道科学，2008，29（1）：7-12.

［6］雷晓燕，张斌，刘庆杰.轨道过渡段动力特性的有限元分析［J］.中国铁道科学，2009，30（5）：15-21.

［7］冯青松，雷晓燕，练松良.不平顺条件下高速铁路轨道振动的解析研究［J］.振动工程学报，2008，21（6）：559-564.

［8］XIA H，CAO Y M，ROECK G DE.Theoretical modeling and characteristic analysis of moving-train induced ground vibrations［J］.Journal of Sound and Vibration，2010，329:819-832.

［9］冯牧，雷晓燕.列车引发建筑物振动试验与数值隔振研究［J］.噪声与振动控制，2009，29（5）：80-86.

［10］涂勤明，雷晓燕，毛顺茂.地铁产生的环境振动及轨道结构减振分析［J］.噪声与振动控制，2014，34（4）：178-183.

［11］雷晓燕.轨道力学与工程新方法［M］.北京：中国铁道出版社，2000：45-46.

［12］Zienkiewicz O C.The Finite Element Method（Third Edition），MC GRAW-HILL，1977.

［13］张斌，雷晓燕.基于车辆-轨道单元的无砟轨道动力特性有限元分析［J］.铁道学报，2011，33（7）：78-85.

［14］雷晓燕，圣小珍.现代轨道理论研究［M］.2版.北京：中国铁道出版社，2008：398-399.

Cross-iterativeAlgorithm and ItsApplication to theAnalysis of Vehicle-track Nonlinear Coupling Systems

LEI Xiao-yan，WU Shen-hua，ZHANGBin

（Engineering Research Center of Railway Environment Vibration and Noise，Ministry of Education，East China Jiaotong University，Nanchang 330013，China）

A model for dynamic analysis of a vehicle-track nonlinear coupling system is established by finite element method.The system is divided into two subsystems，i.e.the vehicle subsystem considered as the secondary spring vehicle model and the track subsystem regarded as the model of three discrete elastic beams.Coupling of the two systems is achieved by equilibrium conditions of wheel-rail nonlinear contact forces and geometrical compatibility conditions.A crossiterative algorithm is presented to solve the dynamics equations of the vehicles-track nonlinear coupling system.In order to accelerate the iterative convergence rate，the relaxation technique is employed to correct the wheel-rail contact force. Comparing with the example in a reference，the correctness of the algorithm is verified.Examples of the vehicle and track vibration induced by the high-speed CRH3 train traveling on ballasted track are given，in which the influences of linear and nonlinear contact and different train speed on the vibration of vehicles and track structure are considered.The results demonstrate that the cross-iterative algorithm has the advantages of simple programming，fast convergence rate，less computation time and high accuracy.The dynamic response obtained by the wheel-rail linear contact model is larger than that by the wheel-rail nonlinear contact model.The increases of the maximum displacement，the maximum acceleration，the displacement amplitude and the maximum acceleration are all within 15%.The increases of the maximum wheel-rail contact force and the wheel-rail contact force amplitude are all within 5%.

vibration and wave；vehicle-track nonlinear coupling；cross-iterative algorithm；wheel-rail nonlinear contact；wheel-rail linear contact；relaxation technique

U213.2+12

ADOI编码：10.3969/j.issn.1006-1335.2016.04.024

1006-1355（2016）04-0113-07

2015-12-25

国家自然科学基金资助项目（51478184）

雷晓燕（1956-）男，教授，研究方向为高速铁路轨道动力学。E-mail:xiaoyanlei2013@163.com

，吴神花（1989-）女，硕士研究生，研究方向为高速铁路轨道动力学。Email:466980214qq.com