中间构架柔性对双层隔振系统隔振特性的影响

刘洋山，孙梅云，闫　兵，陈　俊，周国豪

（1.西南交通大学 机械工程学院，成都 610031；2.唐山轨道客车有限责任公司，唐山 063035）



中间构架柔性对双层隔振系统隔振特性的影响

刘洋山1，孙梅云2，闫兵1，陈俊1，周国豪1

（1.西南交通大学 机械工程学院，成都 610031；2.唐山轨道客车有限责任公司，唐山 063035）

为定量分析中间构架柔性对内燃动力包双层隔振系统隔振特性的影响规律，指导双层隔振系统的优化设计，建立中间构架的有限元模型并进行模态计算，通过与试验模态对比，验证有限元模型的正确性。在Adams中建立考虑中间构架柔性的刚柔耦合系统动力学模型以及将中间构架视为刚体的多刚体系统动力学模型。通过自由振动和扫频分析，得到中间构架柔性对双层隔振系统隔振特性的影响规律。研究结果表明中间构架柔性会使系统固有频率及主模态方向解耦度减小，并使系统幅值响应出现“移频”、“增频”现象，其中低频段以“移频”为主，高频段以“增频”为主，中频段二者同时出现。相关结论可为隔振设计以及耦合振动的有效控制提供动力学方面的参考。

振动与波；内燃动力包；双层隔振；刚柔耦合；自由振动；扫频分析

随着动力机械功率和转速的提高，以及人们对振动舒适性要求的日益严格，宽频带振动的隔离和抑制问题得到普遍的重视。鉴于经典单层隔振系统对于宽频带振动的隔离存在一定局限性，双层隔振系统应运而生，并在舰船、精密设备以及内燃动车上得到广泛应用［1，2］。机组传统双层隔振设计中，一般将机组、中间质量以及基础视为刚体，忽略其在外部激励作用下的变形，相关简化在小功率、低转速、轻载等情况下既能提高设计效率又能保证隔振效果。然而，随着轻质薄化结构在机械制造领域的广泛应用以及相关设备朝着高速、重载、大功率方向发展，振动隔离中中间质量及基础的非刚性问题显得日益突出并得到广泛研究［3］。俞翔根据舰艇机械隔振系统的特点，结合柔性多体动力学理论，推导了柔性板基础上的隔振系统的动力学模型［4］；孙梅云结合国内首次研制的某型内燃动车动力总成，对双层隔振系统的隔振性能进行仿真和实验研究，其中机组和中间构架均视为刚体，力传递率实测值比仿真计算值略大，初步怀疑与机组受到基础、构架和其它部件动力耦合效应的影响有关［5］。

在上述研究的基础上，以某内燃动车动力包的双层隔振系统为研究对象，建立考虑中间构架柔性的刚柔耦合系统动力学模型和将中间构架视为刚体的多刚体系统动力学模型。通过仿真计算和理论分析，探究了中间构架柔性对系统隔振特性的影响规律，力求为双层隔振系统的隔振设计以及耦合振动的有效控制提供动力学方面的参考。

1　系统描述

图1所示为一典型动力包双层隔振系统模型。受车辆结构及空间限制，柴油发电机组和各附属装置（空冷装置、静压泵、滤清器、消音器、膨胀水箱、油箱等）集成安装在一个中间构架上。其中柴油发电机组通过5个一级隔振器与构架弹性连接，空冷装置与静压泵分别采用4个隔振器与构架弹性连接，其余附属装置与构架刚性连接，构架通过4个二级隔振器吊装在车体下方，构成典型的双层隔振系统。动力包各部件通过公用构架有机组合为一个整体，受设备自身激励及路面激励的影响，系统振动具有多振源、宽频带、强耦合的特点。

2　刚柔耦合系统动力学建模

2.1中间构架有限元建模

建立动力包的刚柔耦合系统动力学模型，需首先建立精确的中间构架有限元模型（此处采用Ansys与Hyper Mesh联合仿真），获取其模态中性文件。中间构架主体采用整体箱型拼焊结构，钢板选用低合金高强度结构钢，由于其长、宽远大于厚度，可在抽取中心层后采用壳单元（Shell 181）划分网格；安装四个二级隔振器的端柱是典型的铸铁件，由于其长、宽、高尺寸相当，且该部件承受动力包的所有质量，适合采用实体单元（Solid 185）划分网格；油箱、膨胀水箱、消音器、滤清器等部件与构架刚性连接，且相对构架柔性效应表现不明显，实际建模过程中可采用质量单元（Mass 21），通过设置其质量、转动惯量来模拟相应部件，质量单元与中间构架之间的连接可以通过创建刚性区域来实现。

2.2中间构架有限元模型验证

通过如图2所示的中间构架自由模态试验验证有限元模型精度。参照GB/T 11349.2-2006，借助TST 5916动态信号测试分析系统对中间构架进行模态测试，确定其固有频率及振型。根据频率响应函数计算方法，得到求和后的频响函数如图3所示。根据综合频响函数中稳态点，提取中间构架各阶的固有频率，并将对应频率下的振动形态描述成振型。

图3　求和后的综合频响函数曲线

在Ansys中采用Block Lanczos模态提取方法对有限元模型进行模态计算，并将计算模态与试验模态进行对比。前3阶模态振型如图4所示。其中第1阶为中间构架扭转振型，第2阶为中间构架菱形振型，第3阶为中间构架弯曲跟静压泵安装座横移振型，各阶计算模态振型与试验振型一致。表1所示为中间构架前9阶模态频率的对比结果，可以看出最大相对误差为3.72%，满足建模精度要求；对比结果表明，所建中间构架有限元模型满足建模精度要求，可以进行后续动力包双层隔振系统建模及隔振特性分析。

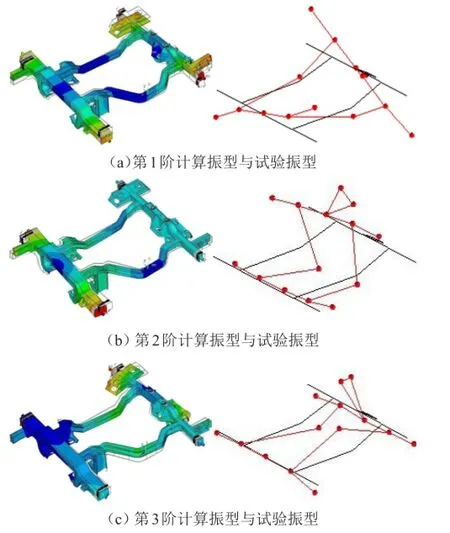
图4　中间构架前3阶模态振型对比

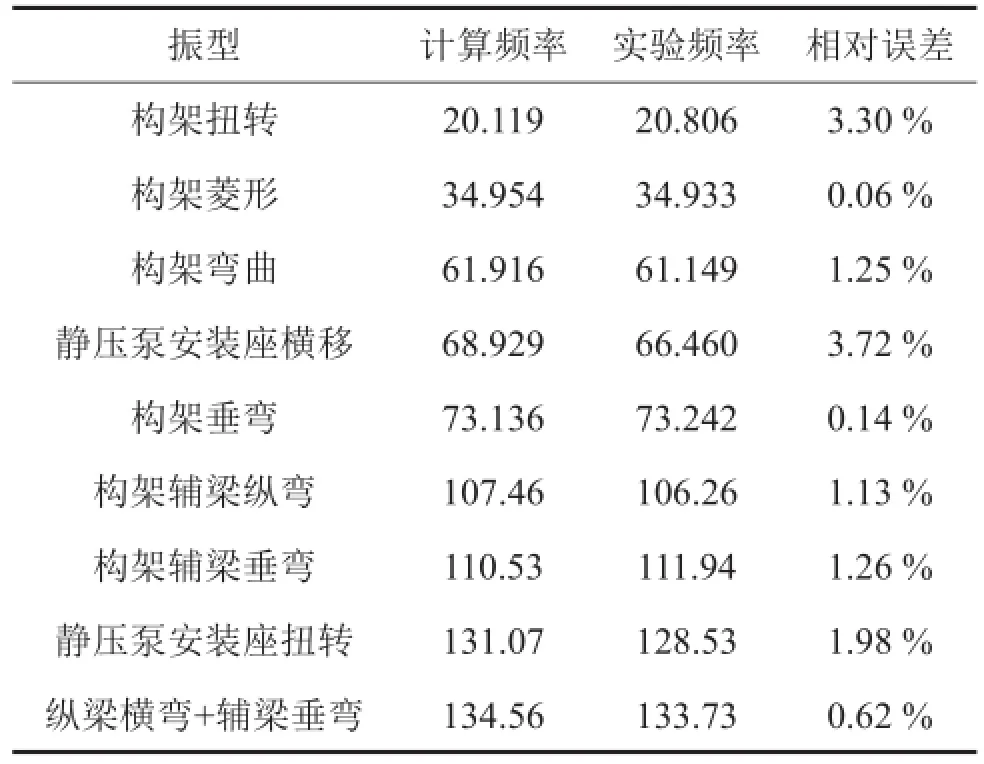
表1　计算模态与试验模态对比/Hz

2.3动力包双层隔振系统建模

该动力包双层隔振系统包括机组与构架的一级隔振、构架与车体的二级隔振以及空冷装置和静压泵的隔振，如果考虑子系统的影响会使系统自由度增加，耦合加剧，不利于研究构架柔性对系统隔振特性的影响。文献［6］探讨了类似动力包中子系统参数对双层隔振系统振动特性的影响规律。研究表明，子系统与机组的质量比小于0.15时，其质量对系统振幅的影响变化率小于10%。文中机组、空冷装置、静压泵的质量分别为2 575.9 kg、223.0 kg、55.0 kg，子系统与机组质量比分别为0.0866、0.0214，均小于0.15，附属装置对系统振动影响较小，在分析构架柔性对系统隔振特性的影响规律时可暂不考虑附属装置对系统的影响。故只针对柔性中间构架与机组组成的双质量系统进行研究。

在中间构架与机组的连接位置建立刚性区域，以便实现柔性体与刚性体的连接。将完善好的构架有限元模型进行模态计算，通过Ansys与Adams接口导出模态中性文件（MNF文件），并将其导入Adams进行柔性体参数编辑，包括装配位置、初始速度、阻尼的设置以及模态的缩减。柔性体编辑完成后，导入机组的刚体文件，并对其质心、质量、转动惯量及装配位置进行编辑。最后，在各隔振器安装位置处借助Bushing模块创建隔振器，赋值优化后的刚度、阻尼。创建好的动力包双层隔振系统动力学模型如图5所示。

图5　动力包双层隔振系统动力学模型

3　双层隔振系统隔振特性分析

3.1自由振动分析

在Adams中分别将中间构架设置为刚体和柔体并进行自由振动计算，根据能量占比提取系统12阶模态振型及固有频率。图6描述了在多刚体和刚柔耦合系统动力学模型下固有频率的差异。其中x、y、z、α、β、γ分别表示纵向、垂向、横向、纵摇、平摇和横摇，1、2分别表示机组和中间构架。如β2表示中间构架平摇。可以看出：构架柔性化以后，系统固有频率整体减小，且随着阶数的增加，偏差量大体呈上升趋势，最大偏差量（第12阶，α2方向）达到4.109 2 Hz，相对误差达到17.03%；最受关注的柴油机倾倒力矩方向频率误差量为0.428 Hz，相对误差为4.19%；除此之外，中间构架柔性对系统β2、y1模态方向对应的固有频率影响较大，相对误差分别达到12.71%、11.91%。

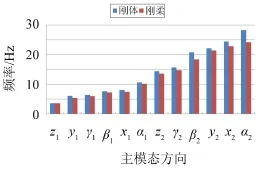
图6　系统固有频率对比

表2描述了中间构架柔性对系统主模态方向解耦度的影响。可以看出：中间构架柔性化处理后，主模态方向解耦度除了z1、y1、y2略增加外，其余方向均减小，即主模态方向系统解耦度降低，振动耦合加剧，系统隔振性能降低。其中x2、α2、β2、z2方向解耦度降低较为明显，最大达到70.19%。机组与中间构架相比，后者主模态方向解耦度变化较大。以系统第11阶模态为例，由系统解耦度可知，多刚体模型中存在x2-x1的耦合模态，解耦度分别为84.11、9.17；刚柔耦合模型中间构架前3阶模态（解耦度分别为3.14、5.22、3.03）与系统刚体模态产生耦合，激发起x2-x1-α2耦合模态，解耦度分别为49.42、5.62、25.52。

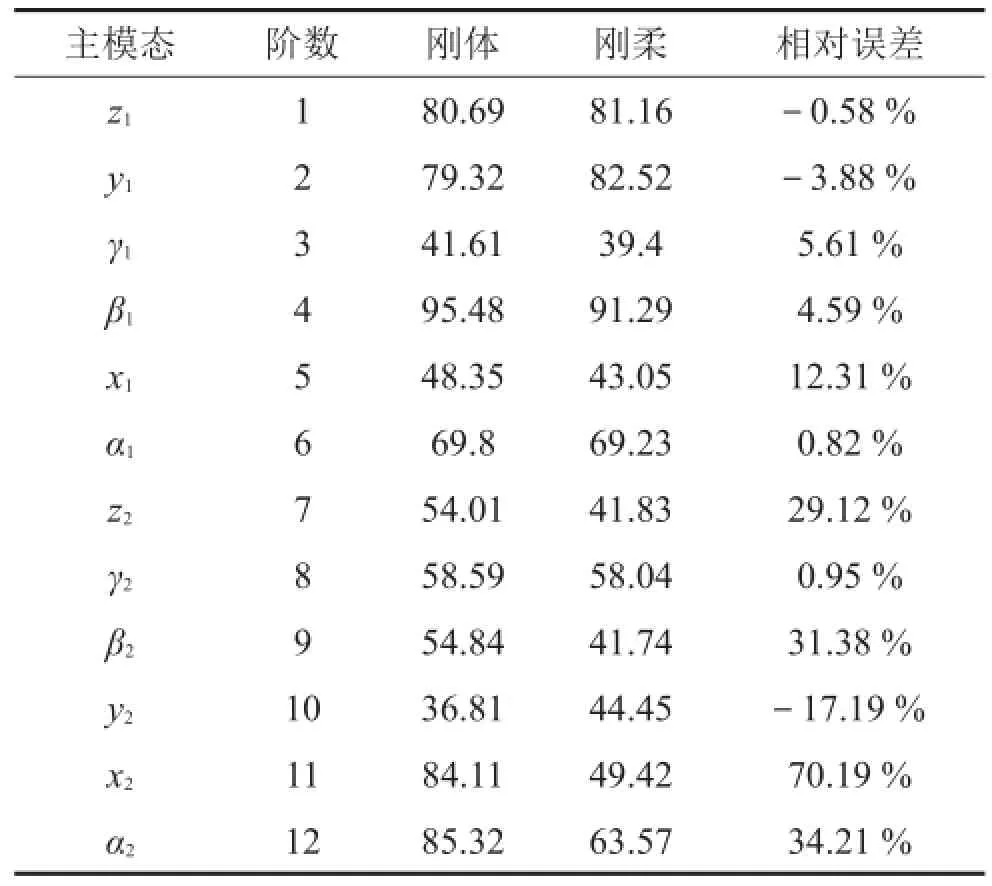
表2　主模态方向解耦度对比

3.2受迫振动分析

考虑到柴油机的3.0阶倾倒力矩是该动力包的主要激振力，在倾倒力矩作用位置建立输入通道，以柴油机最高转速（1 800 r/min）工况运行时的3.0阶倾倒力矩幅值（1 675.11 Nm）为扫频激振力幅值，激励频率范围为0～200 Hz，设置步长为2 000；在机组质心位置、二级隔振器位置、机组及中间构架振动烈度评价点位置布置测点，建立振动加速度及振动速度的输出通道，设置好求解参数后，通过Adams/ Vibration模块分别对多刚体和刚柔耦合系统动力学模型进行受迫振动分析。图7给出了不同模型下中间构架二级隔振器处垂向速度的幅值响应。可以看出：构架柔性化以后，刚柔耦合系统动力学模型的12个刚体振动模态依然明显存在，但已和构架的弹性振动模态有机地结合在一起，系统固有频率及响应幅值有了明显的变化，具体表现在：

（1）刚柔耦合系统动力学模型峰值响应频率较多刚体模型总体减小，出现了所谓的“移频”现象，这主要是由于中间构架柔性化以后，系统等效刚度减小引起的；

（2）中间构架柔性化以后，低频段（20 Hz以下）除了“移频”现象外，系统刚体模态与中间构架结构模态耦合较弱，没有明显的“增频”现象；高频段（大于40 Hz）多刚体模型已无响应峰值，但刚柔耦合模型额外增加了数个响应峰值，出现了“增频”现象，因该频段峰值响应频率较高，初步推测为中间构架结构模态所致。中频段（20 Hz～40 Hz）“移频”、“增频”现象同时出现，因中间构架扭转、菱形模态均出现在该频段，初步推测为中间构架结构模态与系统刚体模态耦合作用的效果。

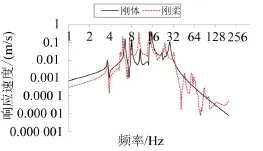
图7　二级隔振器处垂向速度的幅值响应

为验证上述推测，并进一步分析其他点处的受迫振动响应，进行如下分析：考虑到在其余参数不变的情况下，减小机组质量、转动惯量后，它对中间构架及双层隔振系统的耦合影响变弱。当机组质量、转动惯量趋于零时，一级隔振器刚度相对变大，机组与中间构架近似为刚性连接，原来的双质量系统近似为单质量系统，此时系统模态近似为中间构架的约束模态，因此可以利用改变机组质量、转动惯量的方法，从侧面研究中间构架模态在双质量系统模态中的作用。将刚柔耦合系统模型中机组质量、转动惯量变为原来的0.1倍、0.01倍、0.001倍，并分别进行受迫振动分析。图8给出了不同模型下中间构架某一振动烈度评价点处垂向速度的幅值响应。为便于观察低频段响应特性，图9给出了其0～40 Hz范围内的响应。其中NO.1、NO.2分别表示机组在原有质量、转动惯量参数下的多刚体模型和刚柔耦合系统动力学模型，NO.3-NO.5分别表示机组质量、转动惯量变为原来0.1倍、0.01倍、0.001倍时的刚柔耦合系统动力学模型。

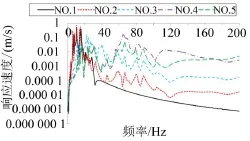
图8　振动烈度评价点处垂向振动速度的幅值响应

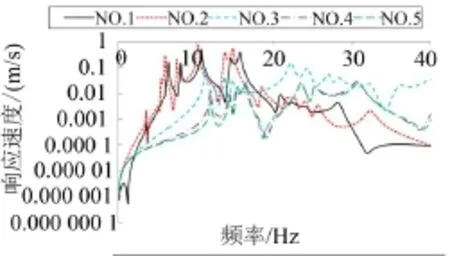
图9　振动烈度评价点处垂向振动速度的幅值响应（0～40 Hz）

比较NO.1、NO.2可以看出：构架柔性化以后，该点幅值响应同样出现了“移频”、“增频”现象，低频段以“移频”为主，高频段以“增频”为主，中频段二者同时出现；比较NO.1-NO.5可以看出：高频段机组质量、转动惯量的减小，只对系统响应幅值的大小有影响，对峰值对应频率几乎无影响，这说明高频段的“增频”现象主要是由构架结构模态主导的；中频段NO.4、NO.5基本重合，且此时机组质量、转动惯量趋于零，系统模态近似为中间构架的约束模态（共三阶），NO.3、NO.2随着机组质量、转动惯量增加，峰值频率增多，模态愈发密集，耦合愈发严重，结合上节解耦度分析的结果，可从侧面证明该频段“移频”、“增频”是机组与中间构架弹性模态耦合作用的结果。结合其它输出通道的结果还可以看出，随着机组质量、转动惯量的增加，高频段（尤其是160 Hz以上）速度响应幅值减小。

4　结语

为定量分析中间构架柔性对内燃动力包双层隔振系统隔振特性的影响规律，指导双层隔振系统的优化设计，建立了中间构架的有限元模型并进行模态计算，通过与试验模态对比，验证了有限元模型的正确性。利用导出的模态中性文件，在Adams中建立了考虑中间构架柔性的刚柔耦合系统动力学模型以及将中间构架视为刚体的多刚体系统动力学模型。通过扫频及自由振动计算，得到了构架柔性对双层隔振系统固有特性的影响规律：

（1）中间构架的柔性效应会导致系统固有频率减小，且随着阶数增加，误差量大体呈上升趋势。

（2）中间构架的柔性效应会使系统主模态方向解耦度降低，振动耦合加剧，系统隔振性能降低。

（3）相对于多刚体模型，考虑中间构架柔性的刚柔耦合系统动力学模型在激励作用下的响应会出现“移频”、“增频”现象，其中低频段以“移频”为主，高频段以“增频”为主，中频段二者同时出现。

（4）随着机组质量、转动惯量的增加，高频段（尤其是160 Hz以上）系统响应幅值减小。

鉴于上述影响规律，在隔振设计时应充分考虑基础及中间构架柔性，合理匹配中间构架与机组质量。低频段可通过调节隔振器刚度等方法抵消“移频”；中频段可通过合理匹配系统模态，尽量避免主要激振力方向以及振动亟需控制方向模态落入该频段；高频段主要为柔性体结构模态，可在中间构架、基础设计时对结构进行总体优化，在轻量化的同时尽可能提高其刚度。

［1］汪玉，陈国钧，华宏星，等.船舶动力装置双层隔振系统的优化设计［J］.中国造船，2001，42（1）：45-49.

［2］孙玉华，董大伟，闫兵，等.双层隔振系统解耦优化研究［J］.振动、测试与诊断，2014，34（2）：361-365.

［3］孙玉国，刘海江，孙玲玲，等.刚柔耦合动力系统固有振动特性研究［J］.振动、测试与诊断，2003，23（1）：48-50.

［4］俞翔，何其伟，朱石坚，等.柔性板基础隔振系统的柔性多体动力学理论建模［J］.噪声与振动控制，2010，30（6）：58-62.

［5］曾锐，孙梅云，孙玉华，等.内燃动车动力总成隔振性能分析［J］.噪声与振动控制，2014，34（2）：89-93.

［6］孙玉华.内燃动车动力包双层隔振设计方法研究［D］.成都：西南交通大学，2013.

Influence of Intermediate Frame Flexibility on the Vibration Isolation Characteristics of a Double Layer Vibration Isolation System

LIU Yang-shan1，SUN Mei-yun2，YANBing1，CHENJun1，ZHOU Guo-hao1

（1.School of Mechanical Engineering，Southwest Jiaotong University，Chengdu 610031，China；2.Tangshan Railway Vehicle Co.Ltd.，Tangshan 063035，Hebei China）

To quantitatively analyze the influence of intermediate frame flexibility on the vibration isolation characteristics of the double layer vibration isolation system of a diesel power pack and guide the optimization design of the system，the finite element model of the intermediate frame is established and its modals are calculated.By comparing with the measurement modals in the testing，the correctness of the finite element model is verified.The dynamics model of the rigidity-flexibility coupled system is built with the flexible intermediate frame considered.And the dynamics model of the multi-rigid-body system is established with the rigid intermediate frame considered.Both models are analyzed by means of ADAMS code.Through the analysis of the free vibration and frequency scanning，the influence of the flexibility of the intermediate frame on the vibration isolation characteristics of the double layer vibration isolation system is obtained.The results show that the flexibility of the intermediate frame can reduce the system’s natural frequency and the decoupling degree of the main modal direction，and cause the amplitude response of the system to yield the phenomena of“frequency shift”and“increasing frequency”.The“frequency shift”phenomenon occurs mainly in the low frequency range，while the“increasing frequency”phenomenon occurs mainly in the high frequency range.Both phenomena occur at the same time in the middle frequency range.These conclusions can provide a reference for vibration isolation design and effective control for coupled vibration.

vibration and wave；internal combustion power pack；double-layer vibration isolation；rigid-flexible coupling；free vibration；sweep frequency analysis

TB535；O328

ADOI编码：10.3969/j.issn.1006-1335.2016.04.020

1006-1355（2016）04-0092-05

2016-01-04

刘洋山（1989-），男，甘肃省张掖市人，研究生，主要研究方向为内燃动力包振动与噪声控制。

闫兵，男，硕士生导师。E-mail:yanbingwd@163.com