声速测量实验方法的改进

李天一　何沃洲　卢子璇　陈　彦　李　华

(1北京航空航天大学电子信息工程学院,北京　100191；2中国人民大学附属中学，北京　100080；3北京航空航天大学物理科学与核能工程学院,北京　100191)



声速测量实验方法的改进

李天一1何沃洲1卢子璇2陈彦3李华3

(1北京航空航天大学电子信息工程学院,北京100191；2中国人民大学附属中学，北京100080；3北京航空航天大学物理科学与核能工程学院,北京100191)

基于虚拟仪器的设计原理，针对振幅法测量声速实验中存在的问题进行了改进，设计了一个基于单片机的声速测量实验系统.该系统中，单片机对接收端信号进行采样并控制端面匀速移动.采集到的数据序列传输到PC机进行中值滤波，由快速傅里叶变换对序列进行预处理，再进行较精确的极值点检测，并通过线性回归方法对结果进行校正.该改进装置提高了实验的准确性和自动化程度，作为原实验方法的有益补充,可应用于大学基础物理实验及课堂演示教学环节，也可应用于声波近场区传播规律的研究.

虚拟仪器；单片机；自动控制；声速测量；振幅法

1　为什么要改进振幅法测量声速实验

图1　振幅法测量声速装置

振幅法测量声速实验是大学物理实验中一个重要内容.振幅法的实验装置如图1所示[1]，S1端面发出平面声波向S2传播，经S2反射之后在两端面之间形成驻波场.场中任意两个信号幅度极大值之间的距离即为该声信号的半波长λ/ 2[2].因此，只要测出信号幅度达到极大时的各位置点，便可以利用下式求出声速v

(1)

式中,v为声速(m/s)；f为声波频率(Hz)；λ为声波波长(m).

然而，在实验操作过程中该方法存在明显不足：首先，振幅极大值的位置依靠目测判断，而波形在极值附近的变化并不明显，这就会产生由于主观因素和示波器的分辨率限制而引入的误差.另外，端面之间的距离通过目视标尺刻度得到，不能得到精确结果[3].为此，本文在振幅法的基础上，对实验仪器进行改进，通过极值点检测算法，设计出基于单片机的声速测量综合实验系统，弥补了原系统存在的上述缺点，提高了测量的准确度，也为教师的课堂实验演示提供了便利.

2　系统设计

针对刻度读取不准确的问题，本文将步进电机与声速测量仪相连，控制端面匀速移动，以步进电机转过的步数间接表示接收端面S2的位移；由单片机控制模数转换器ADC0809对接收端S2的信号进行采集，然后通过RS232串口上传到PC机，进而由软件自动判断极值位置，为准确测量提供可能[4,5].

该系统以单片机为核心，如图2所示.

图2　系统框图

首先通过信号采集电路对接收端的模拟信号进行整流、滤波、放大等预处理.该电路以AD737芯片为核心.接收到信号首先经过高通滤波器，滤除低频干扰信号，使频率较高的有效信号输入到下一级.AD737芯片将交流信号转换为与振幅线性相关的直流信号，并使放大后的信号经分压电路转换为0～5V以满足单片机采样的要求.

单片机通过模数转换器ADC0809采集直流信号，得到对应交流信号的相对幅度，同时均匀地发送脉冲信号，控制步进电机匀速转动，带动由电机驱动的声速测量仪转盘转动，保证了发射端和接收端匀速靠近或远离，再利用串口通信将数据实时地上传到PC机.

PC机接收到数据后，在人机交互界面上实时显示接收信号幅值随S2移动而变化的趋势，并采用中值滤波、快速傅里叶变换等算法进行数据处理，得到各极值的位置后通过线性回归计算半波长λ/2，进而由波长求得声速.

3　算法实现

3.1原理概述

实验过程中，接收端的电压值x(l)是其位置l的连续函数.为方便测量和计算机处理，本实验将其离散化，即步进电机每转动一步，单片机即发送一组数据到PC机，因此总测量次数等于转动步数N，设第n次测量所得电压值为x，则实验结束后可得长度为N的离散序列x[n].在电机匀速转动的前提下，接收器位移与转动步数成正比，即：

(2)

式中,Δl为接收器位移(m)；N为电机转动步数，K为比例系数.

根据振幅法原理，谐振位置对应交流信号振幅的极大值，变换后的直流信号会出现相应峰值，其间距为半波长λ/2.若能在离散域中计算出相邻峰值间的测量次数Δn，即可根据比例关系求得连续域中的半波长为

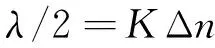
(3)

声速v可由公式(1)、(2)、(3)联立得

v=2fΔnΔl/N

(4)

以上各物理量中，f可由信号源读取，Δl可通过读取声速测量仪的标尺得到，因此处理算法的关键在于求得离散域中相邻峰值间的测量次数Δn.

3.2中值滤波

为减小噪声干扰，首先对数据序列进行数字滤波.综合考虑滤波效果和算法复杂度，本系统采用中值滤波算法，即对每个数据点，以该点为中心把前后m个数据排序，得到[d0，d1，…，dm-1]，用中位数(即dm/2)来代替原数据.适当选择m值，既保证滤波后的数据能反映原信号的变化趋势，又能有效防止尖峰脉冲的干扰.

3.3快速傅里叶变换

在信号序列中，不仅谐振位置存在明显的峰值，其他位置亦可能由于扰动而出现局部极大值，因而不能直接检测峰值点以判断谐振位置.考虑到离散序列x[n]中峰值点的分布具有周期性，故引入离散傅里叶变换，将x[n]分解为若干单一的谐波分量，以获得各谐波的幅度和相位信息[6].为提高计算效率，系统采用以2为基底的快速傅里叶变换(FFT).变换后的离散频域序列X[k]的幅频曲线中会出现明显的峰值，如图3所示.

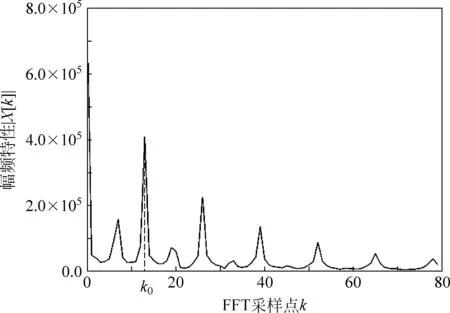
图3　谐振位置检测

除直流分量外的最大峰值对应的横坐标k0代表基频，即离散序列中峰值点的个数，据此求得Δn的估计值为

(5)

考虑到声速测量仪长度有限，峰值点数目k0一般不超过40个且只能取整数，若单纯采用FFT则精度受限.但作为预测量步骤，FFT可为精确测量Δn提供依据，在本系统中仍有存在的必要.

3.4谐振位置检测与线性回归

在FFT的基础上，确定出每个谐振位置对应的峰值点，如图4.创建数组top，首先按照估测周期Δn′，选取一个周期内最大值在时间轴上的对应值，作为第0个峰值点top[0]，其后的第i个峰值点为top[i] (i=1,2,3，…)，则相邻的top[i]与top[i-1]的差约为Δn′，即top[i]=top[i-1] +Δn′,但由于Δn′为近似值，可认为top[i]存在于top[i-1] + 0.9Δn′和top[i-1] + 1.1Δn′之间，将此范围中电压最大值的位置确定为top[i].以此类推，即可求得所有谐振位置.

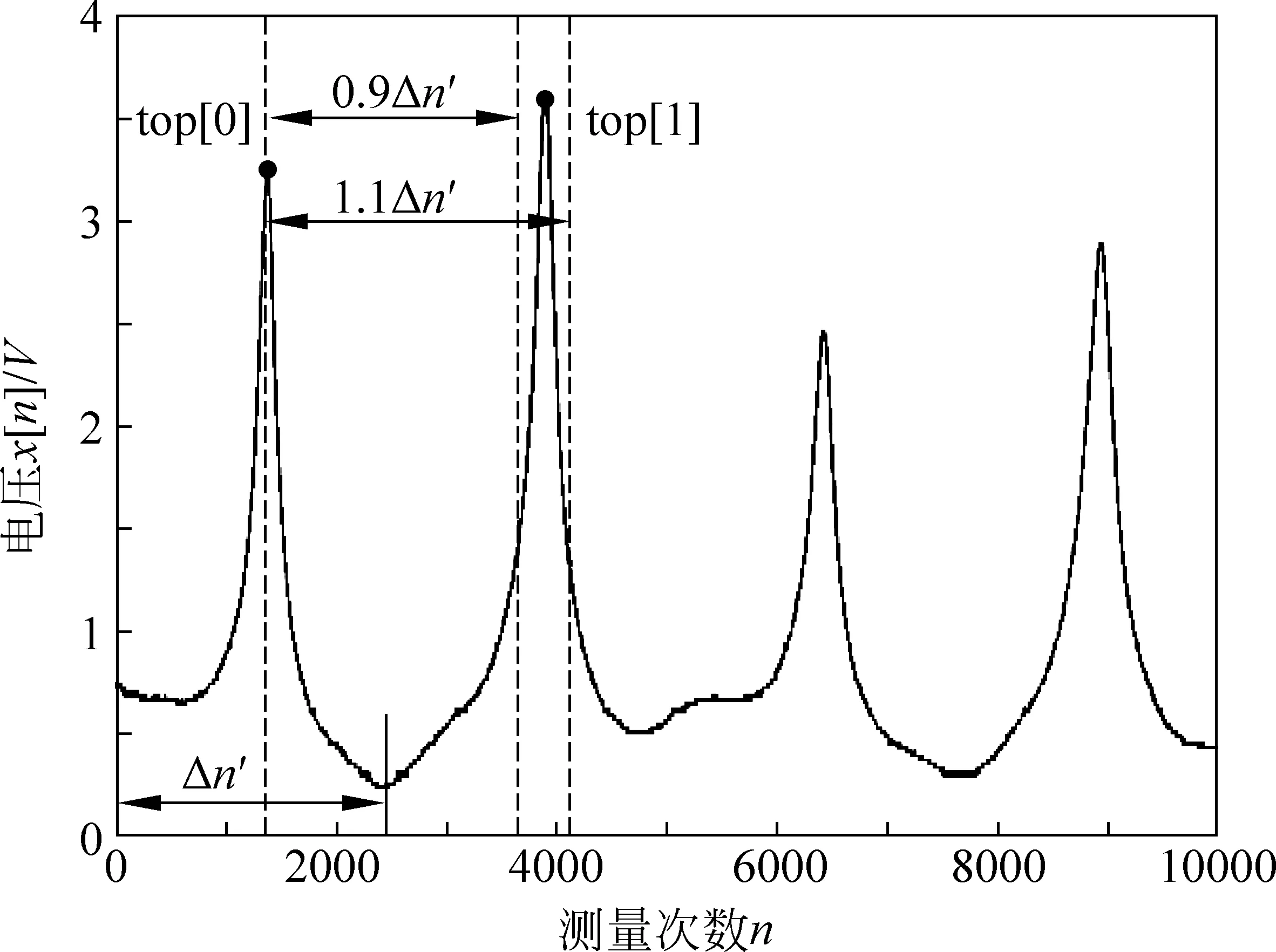
图4　快速傅里叶变换

数组top[0],top[1],…,top[i],…中相邻两项的差应为相邻峰值间的测量次数Δn.受随机因素影响，差值并非严格相等，因此引入一元线性回归进行拟合，从而以较高的精度计算出Δn值.

4　实验结果

以某次实验为例进行以下分析：

总测量次数N=32768，信号源频率f=35.616kHz，实验过程中接收器位移Δl=64.315mm，测得的谐振位置如表1：

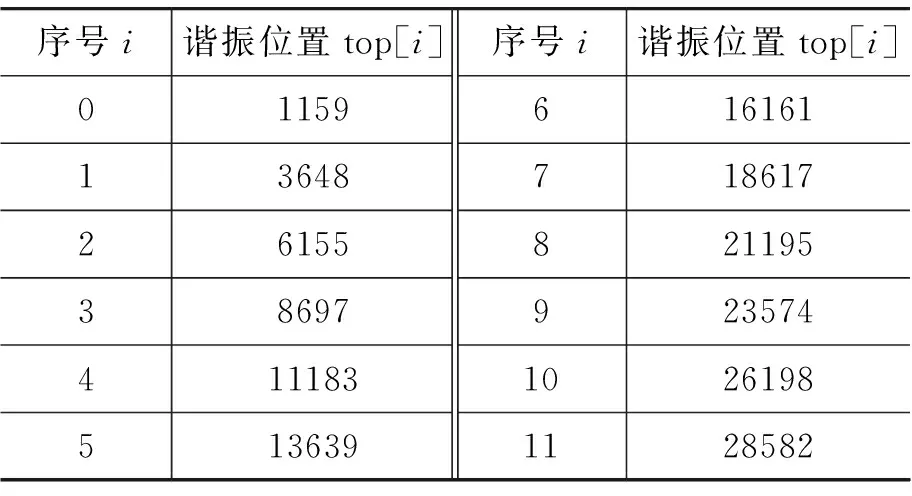
表1　谐振位置检测

经线性回归可得相邻谐振位置间距Δn′=2496.01，代入式(4)中求得声速为

v=2fΔnΔl/N=348.970(m/s)

(6)

实验过程中传感器测得的平均温度为27.77℃，代入空气中的声速公式

vs=331.45(1+t/273.15)1/2m/s

(7)

求得理论值vs=347.891m/s，相对误差η=0.31%.

按上述方法进行多次测试，结果如表2.

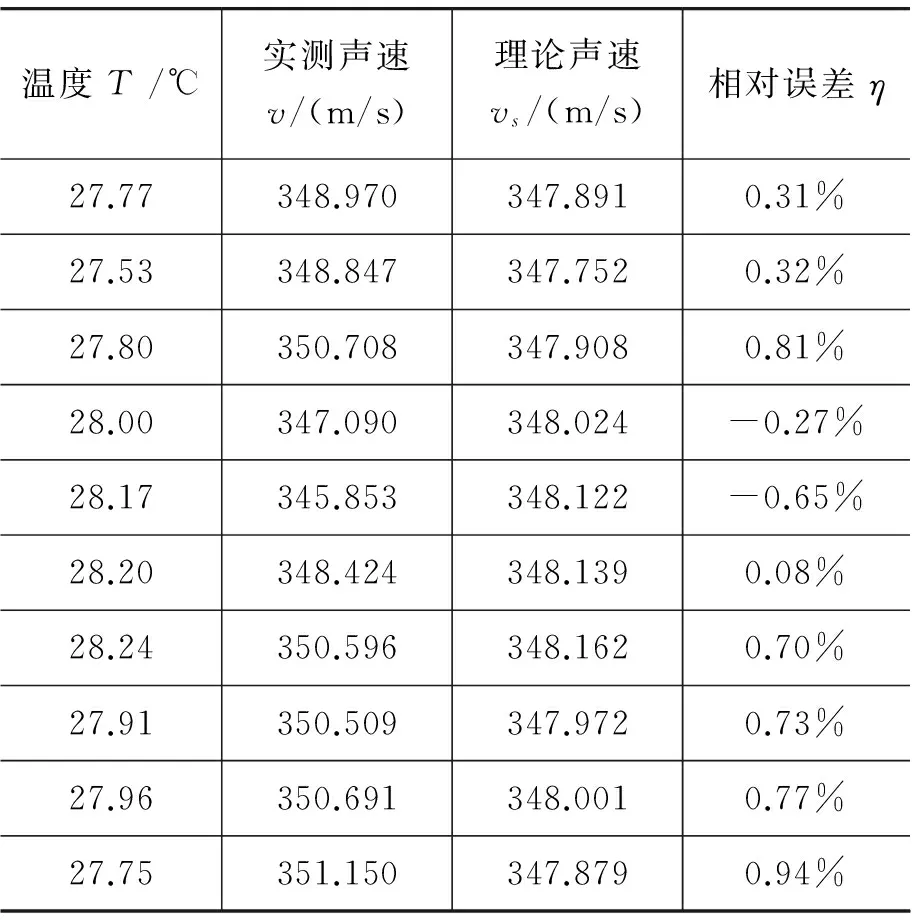
表2　系统测试结果

本系统在实验原理、硬件结构和软件算法方面均采取了减小误差的措施.由实验数据得，各组误差均不超过1%，处于合理的范围，可见本系统具有较高的准确度.误差来源可能包括[7]：

(1) 信号源稳定性有限，实验过程中频率f存在细微的变化；

(2) 步进电机非严格匀速造成所测Δn的误差；

(3) 刻度尺读数造成Δl的误差；

(4) 温度传感器精度有限，测得的温度与环境温度存在偏差使计算的理论真值存在偏差；

(5) 信号采集和处理电路存在微小噪声；

(6) 受实验条件和仪器限制，测量数据有限.

分析多次实验过程，超声波信号源频率f一般为35～40kHz，频率波动在20Hz以内，其误差不超过0.06%；刻度尺最小分度0.01mm，Δl误差不超过0.02%；测定若干次步进电机转速，可得由电机不严格匀速造成Δn误差在0.8%以内；由于谐振位置处电压存在明显的峰值，电路中的微小噪声不会对Δn产生明显影响；单片机所使用的12位温度传感器DS18B20最大测温误差为1℃，代入声速公式求得的理论真值的最大偏差为0.17%，可认为求得的理论真值比较准确.综上所述，本实验的误差主要来源于误差项(2)，声速v的相对误差不超过1%，与实验结果基本相符.

5　结论

与传统实验方法相比，改进后的实验具有以下特点：

(1) 实现自动测量与计算，减少人工干预；

(2) 引入快速傅里叶变换和中值滤波等数字信号处理算法，减小噪声干扰；

(3) 在PC机上实时显示信号与换能器间距的关系曲线，直观形象；

(4) 无需借助示波器，降低对实验设备的要求，节约成本.

该声速测量实验装置可应用在大学基础物理实验及课堂演示教学环节，配合启发式理论讲解，使学生对声速测量的原理和过程获得更直观的认识.也可应用于声波近场区传播规律的研究，以获得声波传播过程的衰减特性数据.在信号采集、测量与数据处理方面，本平台体现了“虚拟仪器”的设计思想.利用模块化硬件和灵活的软件算法代替实体仪器，具有易于开发和调试的优点，并兼备自动测量与演示功能，体现了仪器仪表领域的发展方向[8].

[1]李朝荣. 基础物理实验[M]. 修订版. 北京: 北京航空航天大学出版社, 2013.

[2]康永刚,张秀娥. 对驻波法测声速的讨论[J]. 物理通报，2011(11): 11-12.

[3]刘兴俊,王昆林. 超声波声速测定的三种实验方法比较研究[J]. 实验科学与技术，2011, 9 (2): 184-187.

[4]朱方玺,曹伟然. 声速测量实验仪的改进[J]. 物理实验，2011, 31 (10): 40-43.

[5]张俊玲.声速测量演示实验的设计与实现[J]. 实验科学与技术，2012, 10 (4): 14-16

[6]程佩清.数字信号处理[M].4版.北京: 清华大学出版社, 2013.

[7]陈中钧.超声波声速测量试验中的误差分析[J].实验科学与技术，2005(10): 146-147.

[8]秦树人，尹爱军，刘小峰.现代虚拟仪器[M].北京: 机械工业出版社, 2011.

■

IMPROVEMENT OF SOUND VELOCITY MEASUREMENT METHOD

Li Tianyi1He Wozhou1Lu Zixuan2Chen Yan3Li Hua3

(1School of Electronic and Information Engineering, Beihang University, Beijing 100191;2The Affiliated High School of Beijing People’s Congress, Beijing 100191;3School of Physics and Nuclear Energy Engineering, Beihang University, Beijing 100191)

According to the design principle of virtual instruments, a sound velocity measurement system based on microcontroller unit is realized, which compensates for some problems of the original experiment with amplitude approach. In this system, the microcontroller unit samples the received signals and controls the uniform motion of the receiver. The data array is uploaded to the personal computer (PC), which is firstly processed with median filtering, followed by the fast Fourier transform. Then the more precise detection of extreme points and linear regression for further correction are implemented. In contrast to the manual operation, the system improves the accuracy of the measurement with good effects of human-computer interaction, which complements the original experiment and teaching demonstration, and also can be applied to research on the laws of the acoustic near-zone spread.

virtual instrument; microcontroller unit; automatic control; sound velocity measurement; amplitude method

2015-10-23;

2016-03-22

李天一，男，北京航空航天大学在读本科生.

陈彦，男，实验师 ，主要从事物理实验教学与管理工作，研究方向为测试计量技术及仪器.chenyan@buaa.edu.cn

引文格式: 李天一,何沃洲,卢子璇,等. 声速测量实验方法的改进[J]. 物理与工程，2016，26(3)：29-32.