伺服运动控制轮廓误差补偿技术研究

江　韦　邹俊忠　张　见　卫作臣

(华东理工大学，上海 20023)



伺服运动控制轮廓误差补偿技术研究

江韦邹俊忠张见卫作臣

(华东理工大学，上海 20023)

针对单轴的定位精度问题提出了迭代学习控制方法来减小跟踪误差，并在传统PID-CCC控制器的基础上提出了模糊自适应算法在线自动调整交叉耦合的PID参数。实验证明将该方法应用于轮廓误差补偿，能够提高两轴的协调性能，可以快速地跟踪轮廓参考轨迹，不但很大程度上减小了系统跟踪误差与轮廓误差，还提高了控制系统的鲁棒性。

运动控制；轮廓误差；迭代学习；交叉耦合；模糊自适应

随着高新技术产业和尖端工业技术的发展，运动控制技术及其装备已成为先进制造技术的关键技术和基础装备，在制造业中发挥着不可或缺的作用。而不断提高的任意形状工件加工精度标准使得在交流伺服运动控制系统中，要求对动态响应和定位精度也随之越高，为满足现代化生产加工的需要，提高系统的轮廓加工精度已经成为重要的精度标准。

文献[1]王波等根据光学通用方程的原理构建了针对非球光曲面误差的轮廓误差模型，并且提出了符合此模型的模糊耦合补偿策略，有效地解决了轮廓控制系统中非线性和变形引起的鲁棒性差等问题。文献[2]中李宏胜在仔细分析并总结轮廓误差估计算法后，提出了以模糊算法为基础的在线整定交叉耦合控制参数的整体控制方案，并结合典型的轮廓控制系统来进行实验验证，结果证明了该算法的可行性，在很大程度上减小了控制系统的轮廓误差。文献[3]中周延松在总结了迭代学习和交叉耦合控制方法的基础上提出了串级型系统控制方案，将系统看作串级连接，以三轴数控系统为实验对象进行轮廓误差补偿分析研究，针对空间中直线和螺旋线的仿真对比研究来验证了算法可行性。

根据上述分析，本文基于两轴伺服运动控制系统，提出一种新型的轮廓误差补偿方法。针对单轴运动控制的跟踪误差提出了使用迭代学习控制，对于两轴间的同步运动不协调引起的轮廓误差，进行模糊自适应交叉耦合控制。结合传统的交叉耦合控制自身的优点，在它的基础上，为了减少PID参数对轮廓误差的影响，提出了使用模糊自适应智能算法对PID参数进行在线自整定。

1　轮廓误差的来源与系统的建模

在实际运动控制系统中，由于受电气、制造、机械等多个环节的影响，不可避免的会产生轮廓轨迹误差，通常表现为单轴跟踪误差叠加及多轴协调误差引起的轮廓误差。首先，跟踪误差指的是在单轴运动控制中，理论与实际位置响应之间存在的差值，如数控系统中插补指令脉冲的丢失或者加工过程中的振动、伺服系统的参数设置等各种外界干扰等都可能造成跟踪误差。轮廓误差则指的是在多轴运动控制系统中，由于各运动轴在控制运动中不协调所引起的在轮廓加工制造中实际与理论位置响应的最短距离。由于在高速加工时各运动轴间的参数匹配和协调关系及负载干扰等无法逐项考虑到，轮廓误差必然存在。

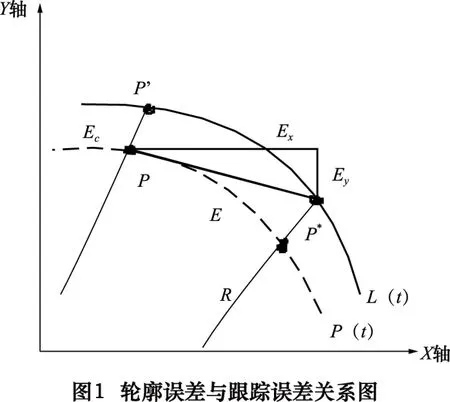
如图1为轮廓误差与跟踪误差关系图：L(t)为指令轨迹；p(t)为实际轨迹；P*为指令位置向量；P为实际位置向量；P′为距实际位置最近的向量点；E为跟随误差向量；Ex、Ey为x、y轴的跟随误差向量；Ec为轮廓误差向量；R为曲率半径。

为了验证方法的可行性和有效性，以下以双轴伺服系统运动控制系统为研究对象，利用MATLAB/Simulink软件进行圆弧轮廓控制仿真实验。仿真采用数控机床的驱动系统X、Y轴传递函数系统模型：

(1)

选取跟踪曲线为半径为1 mm的圆，X、Y两轴为相位相差π/2的正弦波[4]：

(2)

2　单轴迭代学习控制

迭代学习控制(ILC)是一种高级学习控制算法，它是通过逐步迭代和修正以达到或改善相应的控制目的，适合处理重复或周期非线性运动系统以及各种相当高不确定性的强耦合动态系统被控对象[5]。迭代学习控制是以模拟人脑的自我学习和调节为基础，即在没有精确的数学模型情况下，能利用前几次误差信息修正控制输入，以非常简单的算法实现在有限时间内与给定期望输出轨迹的高精度跟踪[6]。目前，迭代学习控制在运动控制领域已得到了广泛运用，并在系统鲁棒性、精确性及很多工程实践中取得了很大成效。

如图2所示为迭代学习控制模块的Simulink子程序。迭代学习的控制方法是将在存储器中存储第k次产生的控制信号μk，并在第k+1次迭代中，将系统的位置误差通过ILC控制器进行处理后产生新的控制信号μk+1，在下一次迭代过程中，经过不断迭代和学习再反馈给系统，以此不断减小位置误差。

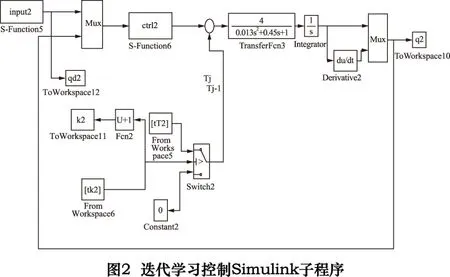
如下式(3)、(4)、(5)分别为基于反馈的迭代学习控制率：

(1)闭环D型

(3)

(2)闭环PD型

μk+1(t)=μk(t)+Kp(qd(t)-qk+1(t))

(4)

(3)指数变增益D型

μk+1(t)=μk(t)+Kp(qd(t)-qk+1(t))

(5)

本文为了在伺服控制系统中突出快速响应的能力，因此将采用式(4)所示的闭环PD型迭代学习控制率。误差ek+1定义为：

ek+1(z)=yr(z)-P(z)μk+1(z)

(6)

故可将控制信号与跟踪误差之间的动态方程改写为：

ei+1(z)=yr(z)-P(z)μi+1(z)=yr(z)

-P(z)μi(z)-P(z)φ(z)ei+1(z)

(7)

进而得出：

(8)

由压缩映射方法可得到该系统的收敛条件为：

(9)

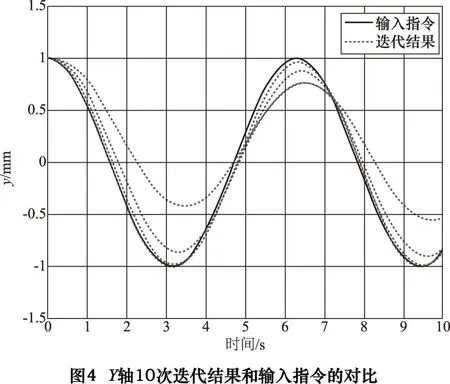
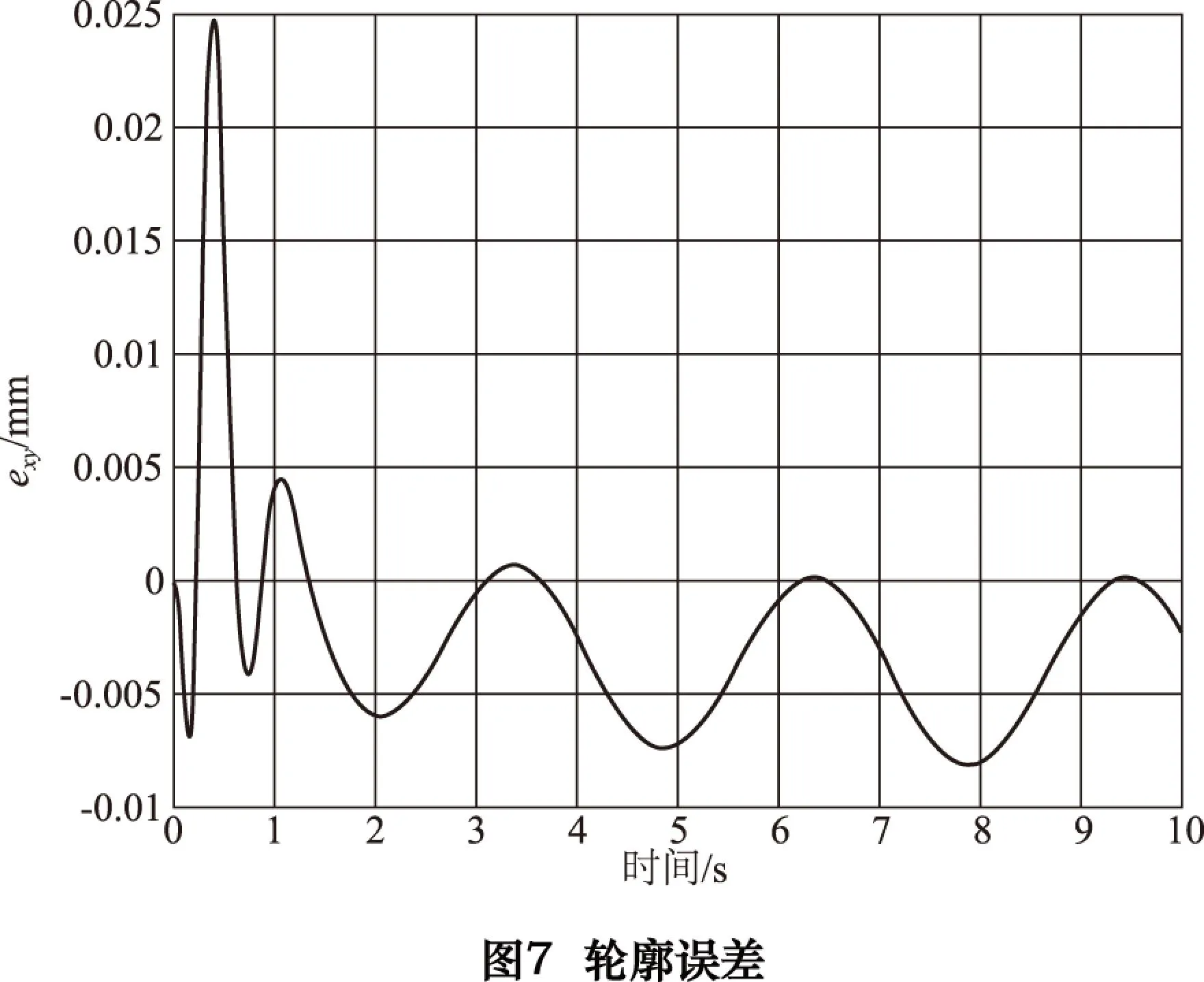
当X、Y轴在无交叉耦合控制器而分别独立控制时，对两运动轴分别采用迭代学习控制。图3、4分别为X、Y轴10次迭代结果与输入指令对比的仿真变化曲线，图5、6分别为X、Y轴随迭代次数变化的跟踪误差曲线，图7为轮廓误差变化曲线。

为了更清晰地分析误差范围，如图7所示为放大刻度尺后的误差，由于不存在交叉耦合控制，两轴在第一次迭代时的轮廓误差都比较大，但随着迭代次数的不断增加，轮廓误差也快速减小；X、Y轴的跟随误差减小速度很快，在经过一次迭代学习控制之后，两轴的跟踪误差快速缩减并分别控制在-0.01～0.01 mm和-0.5～0.5 μm范围内。但显而易见，轮廓误差并没有快速收敛至很小的值，而是存在很大的波动和振荡，这表明仅依靠减小单轴的跟踪误差无法达到减小轮廓误差的效果。并且在实际协调运动控制中，存在复杂性、高精度、非耦合等情况，因此控制系统有着相应的局限性，即当其他轴的速度或者负载发生改变时，无法根据变化轴间不可预见性的动态改变做出实时调整，因此各轴间无法达到很好的协调或同步控制。另外，由于在实际的运动控制系统中，外界环境不稳定且干扰因素复杂，不定会影响各运动轴和系统装置的动态性能。鉴于此，下文提出了模糊自适应交叉耦合控制。

3　模糊自适应PID交叉耦合控制

一般的交叉耦合控制器通常可以分成两部分，其一称作轮廓误差计算模型，用来在线实时计算多轴运动产生的轮廓误差；另外一部分称作轮廓误差补偿分配器，用来将获取的控制信号量根据相应的比例关系再分别反馈补偿到各运动轴。它的基本思想是将多个独立运动的轴看作一个统一的控制系统，首先在各运动轴单独运行控制时获取它的控制信息，以此计算或估计各独立轴协同控制时的轮廓误差，并依据所设置的控制策略来补偿各独立轴的估计跟踪误差后输出，最后经过补偿分配器反馈给各运动轴。对各轴间进行耦合协调控制，使得运动轨迹无限接近指令轨迹，以此来达到减小轮廓误差及提高控制定位精度的目的[7]。

交叉耦合控制方法在实际应用中得到了飞速的发展，非常有效地解决了在轮廓加工和机械制造过程中的很多问题，尤其在高速运动下各运动轴参数不一致和动态不匹配造成加工轮廓变形。传统的交叉耦合控制器主要采用PID算法，通过调整PID参数来调节补偿作用，按照ε在各运动轴的分量来确定权系数后将补偿量分配到各轴。但伺服控制系统是一个非线性时变系统，常规的PID控制器参数在实际应用过程中经常会出现性能不稳定、无法实时整定、无法自适应调节运行工况等问题。并且随着科技进步，对各种控制方法以及控制精度要求的逐渐提高，仅仅依靠传统的交叉耦合控制已经无法满足相应的需求。因而想要取得更好的实际控制效果，首先应该从调整好PID控制器中三种参数之间的关系与作用下手。Kp的作用是提高调节精度和加快响应速度；Ki能消除系统的稳态误差；Kd能改善系统的动态性能。因此本文提出了基于模糊自适应算法的交叉耦合控制方式，在传统的交叉耦合控制器环节增加模糊自适应算法模块，使该系统可以在交叉耦合环节，在变增益分配反馈控制变量前能根据所获取的控制器输入指令的变化在线实时调整交叉耦合的PID控制参数，从而可以快速计算出最佳的误差补偿量，以此来达到进一步减小轮廓误差和控制定位精度的目的。

如图8所示为迭代学习和模糊自适应交叉耦合控制结构框图，Xd、Yd代表输入信号；x、y代表输出信号；Cx、Cy代表关于X轴与Y轴的交叉耦合控制增益；Gx、Gy代表X轴和Y轴的传递函数；Ex、Ey代表X轴和Y轴的跟踪误差；error为待求的轮廓误差。

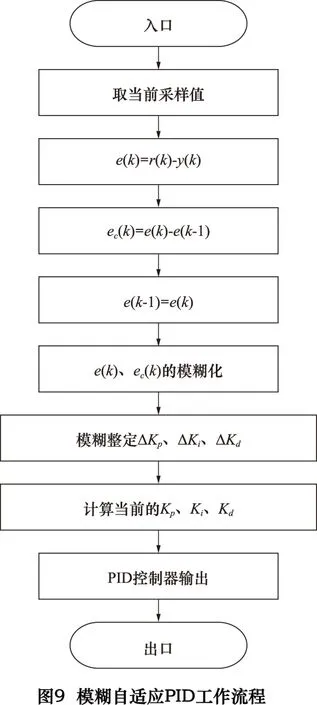
在传统PID控制器的基础上，用模糊集来表示控制规则的条件和操作，并将这些模糊控制规则以及相关信息存储在计算机知识库中，继而计算机凭借控制器中实际输入指令的变化与控制系统的响应情况，采用模糊推理机制，即能够得到对PID参数的在线实时自调整[8]。自适应模糊PID控制器是通过将误差e以及误差变化率ec的改变作为输入变量，也就是说可以根据运动控制中各独立运动轴所产生的轮廓误差大小及变化量实现PID控制参数实时优化，进而通过调整交叉耦合控制器的补偿量与各运动轴间的分配比例关系，满足e和ec对PID参数自整定在不同时刻的要求。设计模糊自适应控制模块的核心是建立合适的模糊规则表，这需要依靠归纳工程设计人员的长期实践积累的技术知识和操作经验，然后用控制规则模型化，得到模糊规则控制表，针对Kp、Ki、Kd3个参数来分别进行整定。如表1、表2、表3所示。可根据如下方法进行Kp、Ki、Kd的自适应校正。

表1Kp的模糊规则表

ecΔKpe NBNMNSZOPSPMPBNBPBPBPMPMPSZOZONMPBPBPMPSPSZONSNSPMPMPMPSZONSNSZOPMPMPSZONSNMNMPSPSPSZONSNSNMNMPMPSZONSNMNMNMNBPBZOZONMNMNMNBNB

表2Ki的模糊规则表

ecΔKpe NBNMNSZOPSPMPBNBNBNBNMNMNSZOZONMNBNBNMNSNSZOZONSNBNMNSNSZOPSPSZONMNMNSZOPSPMPMPSNMNSZOPSPSPMPBPMZOZOPSPSPMPBPBPBZOZOPDPMPMPBPB

表3Kd的模糊规则表

ecΔKpe NBNMNSZOPSPMPBNBPSNSNBNBNBNMPSNMPSNSMBNMNMNSZONSZONSNMNMNSNSZOZOZONSNSNSNSNSZOPSZOZOZOZOZOZOZOPMPBNSPSPSSPPSPBPBPBPMPMPMPSPSPB

如下模糊集上的论域定义了e和ec变化范围：

参数修正公式：

(10)

(11)

(12)

为了更方便直观地比较系统地控制效果，以下将分别对两种控制方式进行simulink仿真：单纯交叉耦合控制和基于模糊自适应交叉耦合控制。其中采样时间t为10 s，修正中的参数初始值分别为：Kp=2，Kj=0.5,Kd=2。

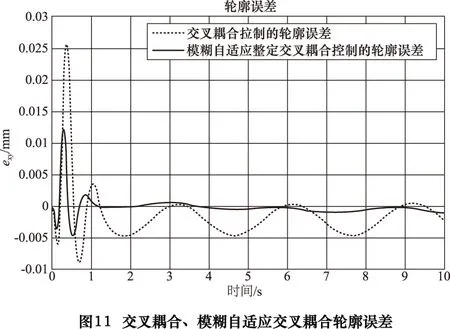
如图10所示为经交叉耦合、模糊自适应交叉耦合补偿之后的X、Y轴轮廓示意图。图11所示，虚线和实线分别代表经交叉耦合控制和模糊自适应整定交叉耦合控制的轮廓误差，从图中可以看出，两种控制方式都能在第一次迭代后快速响应将轮廓误差控制在很小的范围之内，但虚线的超调量达到了0.026 mm，而实线的超调量仅在0.013 mm，是仅用虚线时的1/3。并且在仅采用交叉耦合控制情况下，系统轮廓误差在经过第一次迭代后存在明显的波动和振荡，仅能将误差控制在-0.005～0.005 mm范围内，回复时间太长。显而易见，当采用模糊自适应交叉耦合控制后，轮廓误差在经过第一次迭代后快速趋于平稳状态，调节时间较短，误差也随之收敛至仅为1 μm。在允许误差范围内。

根据以上实验结果可知，在交叉耦合控制器基础上加入模糊自适应算法模块，通过对PID参数实时整定有效地削弱了两轴间速度不匹配和运动不协调所引起的轮廓误差，减小了多种负载扰动在实际运行环境中对控制系统的影响，并提高了两轴间的协调控制的性能，很大程度上减小了系统的跟踪误差和轮廓误差。同时加快了系统对轮廓轨迹的响应能力，缩短了反应时间，使运动轴能够更加精确地跟踪参考轨迹，并提高了系统的稳定性和鲁棒性。

4　结语

先进的控制算法不断地应用于轮廓加工领域以实现高精度的加工要求，本文利用迭代学习控制及时补偿单轴运动带来的跟踪误差，同时利用交叉耦合控制来减小多轴之间协调或同步运动带来的轮廓误差，进一步抑制实际控制中很多不确定因素对控制系统带来的动态性能的影响；加入模糊自适应智能算法实时整定PID控制器参数，缩短了轮廓误差补偿的时间，且补偿过程平稳，不会导致发生振荡，提高了控制加工质量以及运动系统精度。

[1]Wang L, Jin F, Sun Y. Contour control for direct drive XY table[C]. International Conference on. Mechatronics and Automation, 2009.

[2]滕福林,李宏胜.数控机床轮廓误差的插补预测补偿控制研究[J].组合机床与自动化加工技术,2012(1)：47-50.

[3]周延松. 三轴数控系统的轮廓误差补偿方法研究与实现[D].杭州：浙江工业大学,2013.

[4]许强强. 双轴进给伺服交叉耦合控制的研究[D].广州：广东工业大学，2011.

[5]李仁俊,韩正之. 迭代学习控制综述[J]. 控制与决策,2005(9):961-966.

[6]刘松国. 六自由度串联机器人运动优化与轨迹跟踪控制研究[D].杭州：浙江大学,2009.

[7]王丽梅,武志涛,孙宜标,等. 直接驱动XY平台轮廓误差分析及法向交叉耦合控制[J]. 电机与控制学报,2010(9):63-68.

[8]张泾周,杨伟静,张安祥. 模糊自适应PID控制的研究及应用仿真[J]. 计算机仿真,2009(9):132-135,163.

(编辑孙德茂)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Research of contour error compensation technology based on servo motion control

JIANG Wei, ZOU Junzhong, ZHANG Jian, WEI Zuocheng

(East China University of Science and Technology, Shanghai 200237, CHN)

This paper proposes an iterative learning control to reduce the tracking error aiming at the single axis positioning accuracy problem. Furthermore, a fuzzy adaptive algorithm is proposed to automatically adjust the PID parameters of cross coupling on the basis of the traditional PID-CCC controller. Experimental results show that compensating contour error with this method improves the performance of two-axis coordinate, shortens the track time of reference trajectory, enormously reduce both the system tracking error and contour error as well as improve the robustness of the system greatly.

motion control; contour error; iterative learning; cross coupling; fuzzy adaptive

TH161+.5

A

江韦，女，1991年生，研究生在读，研究方向为伺服运动控制。

2015-12-8)

160419