Kossel 3D打印机精度影响因素及微调方法研究*
2016-08-31袁泽林黄纪刚张文君谢志豪
袁泽林 方 辉 黄纪刚 张文君 谢志豪
(四川大学制造科学与工程学院,四川 成都 610065)
Kossel 3D打印机精度影响因素及微调方法研究*
袁泽林方辉黄纪刚张文君谢志豪
(四川大学制造科学与工程学院,四川 成都 610065)
Kossel 3D打印机是一种并联式开源打印机,具有快速打印、噪音小、能自我复制、扩展性好的优点。但是在其装配和使用过程中,微调是一个比较困难又对其性能、打印精度影响较大的问题。为解决这一问题,在对Kossel打印机进行结构分析的基础上,研究了其Arduino控制器Marlin固件的运动参数,分析了该型打印机的精度影响因素,并对打印平台微调的调平方法和调运动参数方法进行了分析和实验验证,提出了该型打印机微调方案,为进一步提升打印精度提供了可行的技术支持。
并联式3D打印机;Kossel;Marlin;Arduino;调平;运动参数
Kossel 3D打印机是一种RepRap 3D打印机[1],其微调直接关系到打印精度,是该型打印机设计制造中最为关键的部分,在机械及软件部分分别需要调平[2]和调运动参数。调平采用的方法有手动调平及自动调平,自动调平又包含Z探针调平、FSR调平等;而对于调运动参数目前尚无明确的方法和步骤,调整需耗费较长时间。本文旨在通过对打印机的运动进行分析,得出较具体的手动微调方案,对Kossel打印机的快速构建和精度稳定性的提升提供可能的技术支持。
1 Kossel运动原理分析
1.1几何原理分析
Kossel打印机及模型如图1所示,类似并联机床[3],运动部分由滑车、斜杆、打印头等通过强磁球或鱼眼轴承连接,滑车通过电动机——皮带传动运动。在打印过程中,Arduino[4]控制电动机转动,使3个滑车A、B、C分别在A塔、B塔、C塔上运动,通过斜杆转化为打印头的运动;三塔顶端各装有限位开关,打印前滑车要回到滑塔顶端,滑车顶端的调平螺丝触碰开关实现回零。

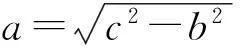
微调打印机的目的是让打印头与滑车的移动符合上述理论曲线,达到相应的精度,所以微调除了机械部分的调平,应主要调整b、c两项参数。

1.2Marlin固件主要参数
Kossel打印机采用Marlin固件[6]进行控制,其主要配置文件为“Configuration.h”,其中对打印机精准运转起关键作用的参数有以下几个(如图4):
DELTA_DIAGONAL_ROD:图中标注1(c),斜杆两端球心间距离。
DELTA_SMOOTH_ROD_OFFSET:图中标注2,打印头中心到滑塔轴心的水平距离。
DELTA_EFFECTOR_OFFSET:图中标注3,打印头中心到斜杆下端球心间水平距离。
DELTA_CARRIAGE_OFFSET:图中标注4,滑塔轴心到斜杆上端球心间水平距离。
DELTA_RADIUS:图中标注(b),上述三个参数相减得到(DELTA_SMOOTH_ROD_OFFSET-DELTA_EFFECTOR_OFFSET-DELTA_CARRIAGE_OFFSET)。
DELTA_PRINTABLE_RADIUS:给定的最大打印半径(小于热床半径,防止打印头撞到滑塔,未在图中表示)。
以上参数皆在打印机回零状态下测量,由图4可知,c=DELTA_DIAGONAL_ROD,b=DELTA_RADIUS,而参数3、4较参数2易测量,应精准测量后写入固件保持不变,于是控制b误差的关键就在于控制参数2即DELTA_SMOOTH_ROD_OFFSET的误差。

2 Kossel运动偏差分析
由于b、c值的测量误差,造成打印头在作直线运动时可能发生两种偏差,分别定义为移动偏差和路径偏差。移动偏差是指打印头实际移动长度与理论不符,可能出现长度缩放现象;路径偏差是指打印头实际运动路径与理论不符,水平运动时形成凹陷或凸起路径。
2.1移动偏差产生机理及影响因素分析
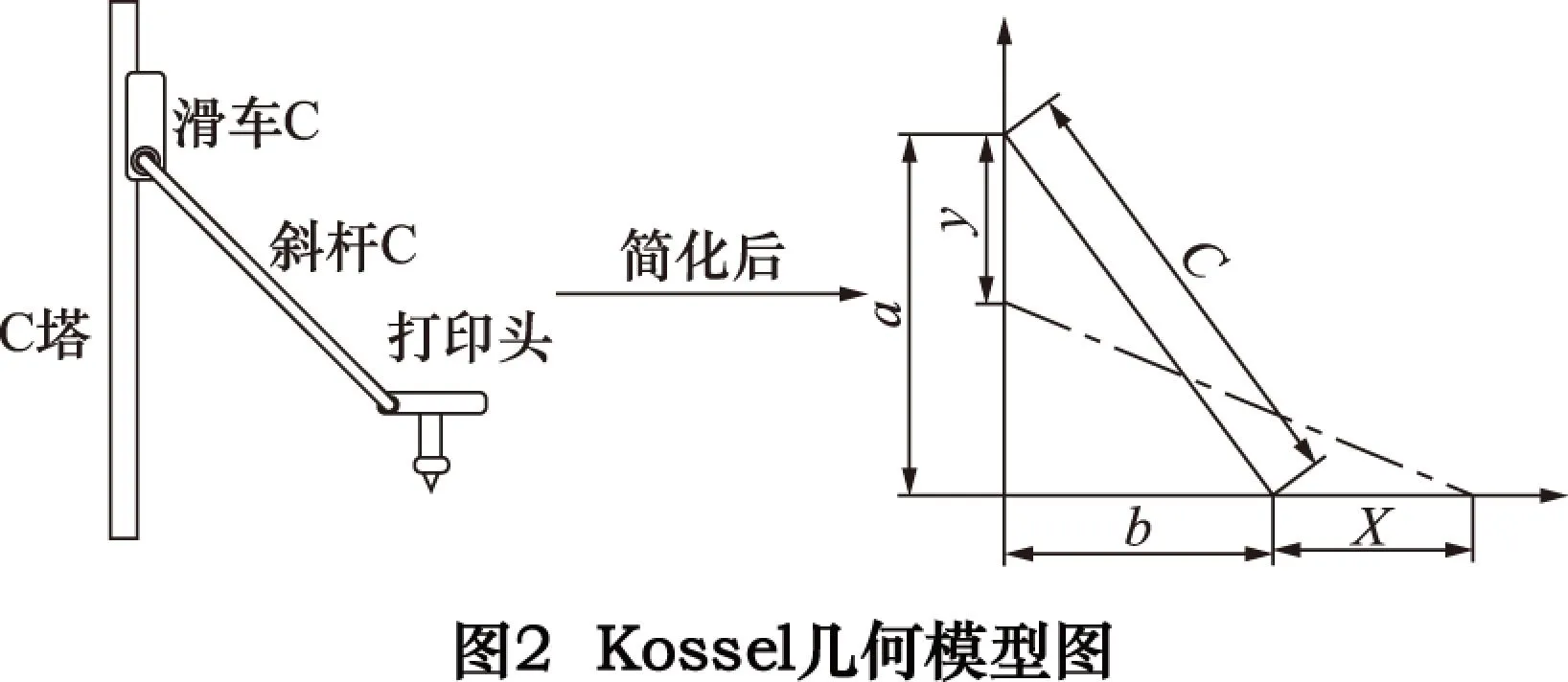
首先给定最大打印半径R(小于b和c-b中较小的一个),如图5,在x∈(-R,R)的范围内,研究实际运动曲线与理论曲线的差异。现采用控制变量法分别研究b、c的误差对打印头实际运动产生的影响。
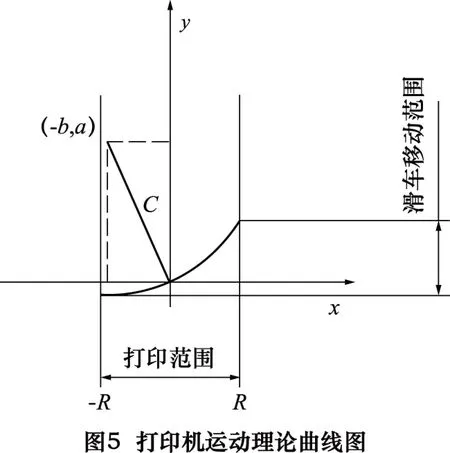
2.1.1b值误差对打印头运动的影响
(1)令:c的测量值=c的实际值,若b的测量值(设为b′)>b的实际值,如图6a,“运动曲线”为机械部分实际运动曲线,“计算曲线”为Marlin固件实际计算产生的曲线。当要求打印长度为x时,Marlin计算后控制滑车移动y′,打印头实际打印长度(设为x′) > 要求长度,所以可得到结论,当b的测量尺寸偏大时,打印整体尺寸偏大。
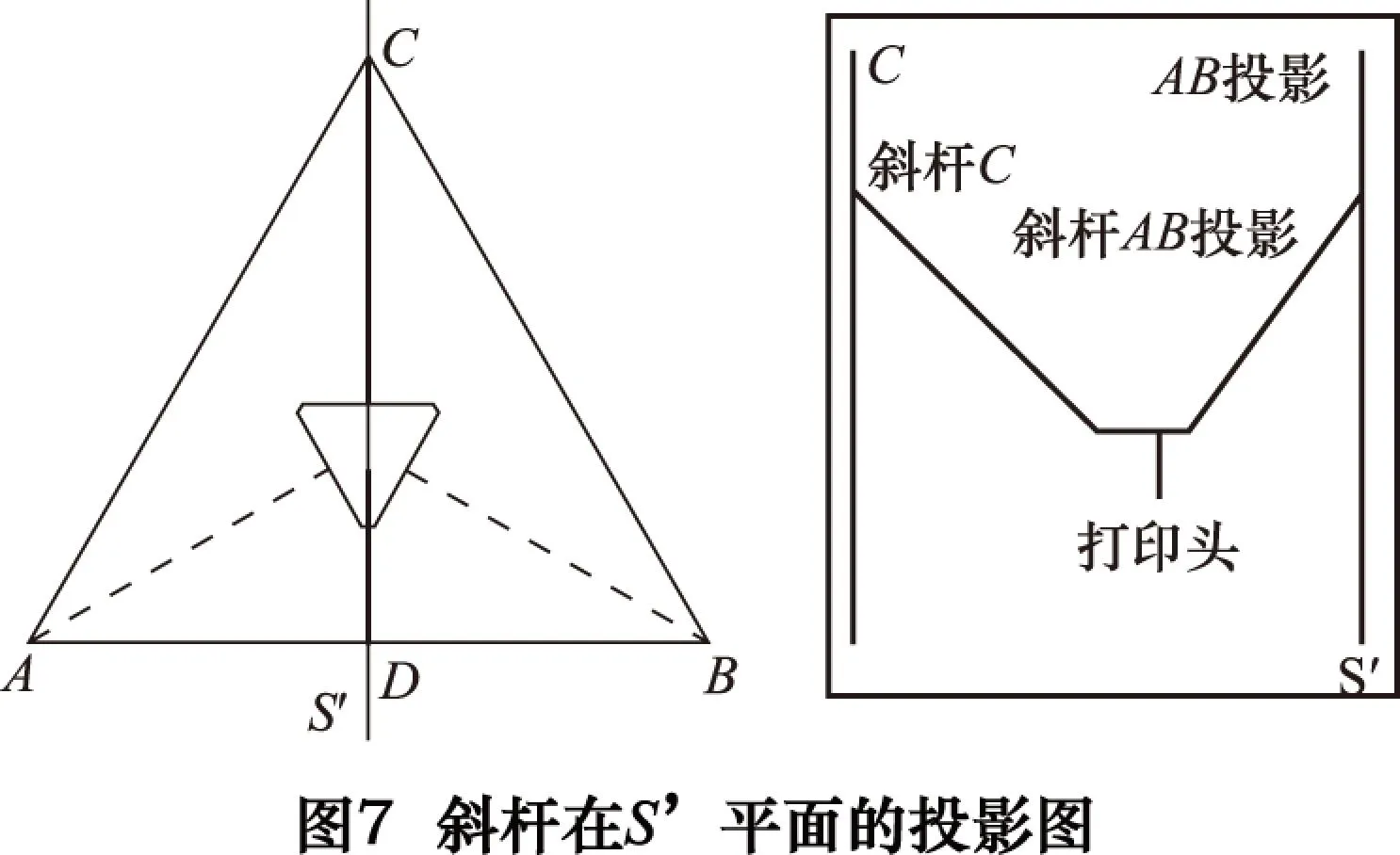
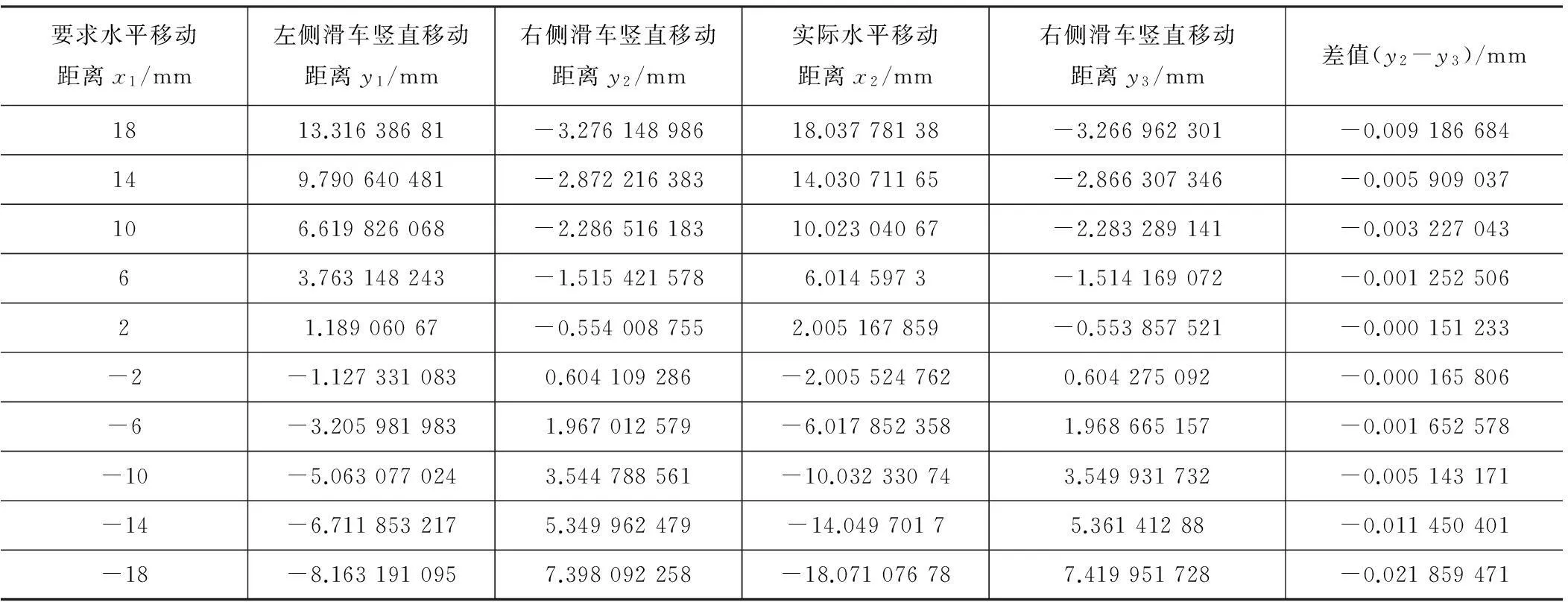
(2)令:c的测量值=c的实际值,若b的测量值(设为b″) 综合以上两点分析可知,当b的测量尺寸偏小时,打印整体尺寸偏小;当b的测量尺寸偏大时,打印整体尺寸偏大。 2.1.2c值误差对打印头运动的影响 (1)令:b的测量值=b的实际值,若c的测量值(设为c′) >c的实际值,如图6c。与上一小节分析相同,当c的测量尺寸偏大时,打印整体尺寸偏小。 (2)令:b的测量值=b的实际值,若c的测量值(设为c′) 综合以上两点分析可知,当c的测量偏小时,打印整体尺寸偏大;当c的测量偏大时,打印整体尺寸偏小。 2.2路径偏差的产生机理及影响因素分析 根据投影的相关原理,在打印机俯视图中,作一垂直于水平面且与打印头运动方向重合的平面S,三根斜杆的移动均可按比例折算为在S平面上各投影的移动,而滑车在各自滑塔上的运动则会按1:1的比例投影。为简化分析,重新做S′平面,使S′平面与斜杆C重合,设打印头沿CD方向运动,将斜杆A、B投影到S′平面上,如图7所示。 为分析打印头路径偏差,拟在S′平面中采用以下方法进行计算: (1)给定参数b、c作为机械部分的实际值。 (2)固定参数c,将参数b适当增大或减小(或固定参数b,将参数c适当增大或减小)作为测量值用于模拟Marlin固件中的计算。具体方法是让打印头水平移动一个定值x1,计算此时的左右滑车移动距离y1和y2,这两个值作为Marlin固件将要控制滑车移动的距离。 (3)将参数b(或c)还原后用y1值计算此时机械部分的实际水平移动距离x2,并由此得到右侧滑车实际移动距离y3,该值为无控制下为保证打印头水平运动当左滑车移动y1时右滑车移动的距离,求出y2与y3的差值。 (4)重复多次计算后绘制横坐标和纵坐标分别为x1和上述差值的曲线图。若曲线均在横坐标以下,则打印头在水平运动时的路径是凹陷的,反之则是凸起的。 (5)根据该判断并结合参数b、c与实际值差值的大小可得到参数b、c对路径偏差的影响。 表1及图8[7]为给定参数b=50 mm和c=100 mm时,固定参数c并将参数b适当增大后计算得到的数据。 经大量计算验证,当参数b测量值大于实际值或c测量值小于实际值时,曲线均在x轴以下,则打印头水平移动的路径为凹陷路径;当参数b测量值小于实际值或c测量值大于实际值时,曲线均在x轴以上,则打印头水平移动的路径为凸起路径。 综合以上分析,在微调Kossel 3D打印机时,可以根据打印路径的凸起和凹陷,对打印尺寸将偏大还是偏小进行预测,通过对参数b、c进行调整,能够有效减小相关运动误差,提高打印精度。 Kossel的调平是调运动参数的前提,是通过调整机械部分以保证打印机热床平面与滑塔A、B、C上的3个限位开关所确定的平面保持平行。目前常用的调平方法有两种,下面分别介绍并进行优选。 3.1方案介绍 (1)以热床平面为基准,调整滑车 表1路径偏差计算数据记录表 要求水平移动距离x1/mm左侧滑车竖直移动距离y1/mm右侧滑车竖直移动距离y2/mm实际水平移动距离x2/mm右侧滑车竖直移动距离y3/mm差值(y2-y3)/mm1813.31638681-3.27614898618.03778138-3.266962301-0.009186684149.790640481-2.87221638314.03071165-2.866307346-0.005909037106.619826068-2.28651618310.02304067-2.283289141-0.00322704363.763148243-1.5154215786.0145973-1.514169072-0.00125250621.18906067-0.5540087552.005167859-0.553857521-0.000151233-2-1.1273310830.604109286-2.0055247620.604275092-0.000165806-6-3.2059819831.967012579-6.0178523581.968665157-0.001652578-10-5.0630770243.544788561-10.032330743.549931732-0.005143171-14-6.7118532175.349962479-14.04970175.36141288-0.011450401-18-8.1631910957.398092258-18.071076787.419951728-0.021859471 注:规定在S′平面中x轴向右为正,y轴向下为正。 如图9a,首先调整热床周围3个调节螺丝来使其水平,之后以热床平面为基准,依次调节滑车调平螺丝,使回零状态下的3个滑车上的3个位置相同的点确定的平面(简称滑车平面)与热床平面尽可能保持平行。 该方案的优点是,在装配过程中限位开关的位置不需要精确保证,只需依靠滑车调平螺丝即可实现调平;缺点是,当热床水平度较差时,滑车平面不水平,从而使3根斜杆上端不处于同一水平面,导致整体结构与Marlin固件算法不匹配。当热床水平度较差时,可能产生较大打印偏差。 (2)以顶部限位开关所在平面为基准,调整热床 如图9b,首先在装配过程中严格保证顶部限位开关的位置,使3个限位开关确定的平面尽可能水平。3个滑车调平螺丝旋至同一长度并固定,之后将热床平面调至与滑车平面平行。 这种方案由于斜杆上端位于同一水平面,避免了方案(1)中打印机结构与Marlin固件算法不匹配的问题,同时避免了调节时滑车调平螺丝长度不易控制的问题;其缺点是对装配精度要求非常高,其次是运用三点调平法[8](将于3.2节中说明)时三点位置不易计算。 3.2实现热床平面与滑车平面平行的方法——三点调平法 以上两种方案的核心都是使热床平面与滑车平面保持尽可能平行,可用三点调平法达到该目的。所谓三点调平法,是将圆形热床用过原点的直线三等分,建立如图10示坐标系,其中Z轴过原点垂直于纸面向外。当给定最大打印范围半径R时,可在原点到滑塔A、B、C的方向上分别确定一点,在该点上,对应斜杆与滑塔夹角最小。通过将打印头与这三点接触来确定三点的Z坐标,进而按方案(1)或(2)调整,最终使得三点Z坐标相同,完成调平。 下面使用方案(1)进行具体调平操作。首先在回零状态下测量打印头至热床的大约垂直距离为293.6 mm,在Marlin固件中给定测量过的参数b=106.3 mm,c=216.9 mm,最大打印半径R=85 mm,设定MANUAL_Z_HOME_POS为294.0 mm(略大于垂直距离测量值是为了读取打印头接触热床时正确读数)。计算三点坐标为C(0,85),A(-73.6,-42.5),B(73.6,-42.5)。打开Pronterface软件,连接打印机,回零,控制Z轴下降至距热床3mm的位置,然后输入命令“g1 x0 y85”到达测定位置,在热床上垫一张A4纸,让喷头以0.1 mm的行程往下降,直到A4纸刚好可以抽出且略有阻力,这时候输入命令“m114”,记下Z值,然后抬高打印头,再对下一个点进行测量。测得3个点Z值分别为A=1.13 mm,B=0.98 mm,C=1.07 mm。分别调节三滑车调平螺丝直到测得的三点Z值都为1.00 mm,然后将MANUAL_Z_HOME_POS更改为293.0 mm后重新上述测量,发现三点Z值变为A=0.00 mm,B=0.00 mm,C=0.00 mm,此时热床平面已与滑车平面平行,即调平完成。归纳来讲,当测得的三点Z值不同时,要通过调节滑车的调平螺丝使之变为同一个正值,再将MANUAL_Z_HOME_POS减掉该正值得到新的MANUAL_Z_HOME_POS并写入固件,即可完成调平。 对于方案(2),由于热床调节螺丝与A、B、C三点位置不同,需要用调节螺丝与热床中心的连线将热床均分三份,并求出与最大打印半径交点的坐标A′、B′、C′进行测量,测量过程大致相同,调平时通过热床调节螺丝完成调平。 另有六点调平法,即采用三点调平后再用反向的三点进行检验是否调平。 调整运动参数是Kossel打印机能实现精确打印的最重要的环节,是将存在偏差的计算曲线逐步修正到与运动曲线吻合的过程。具体而言,就是将测量得到的参数b、参数c不断修改,使之最终与两参数的实际值吻合的过程。 根据前述Kossel运动偏差分析的相关内容可知: (1)当打印路径为凹陷状路径时,打印尺寸偏大,需减小参数b或增大参数c。 (2)当打印路径为凸起状路径时,打印尺寸偏小,需减小参数c或增大参数b。 在进行具体调节过程前首先对斜杆长度(DELTA_DIAGONAL_ROD)进行分析。斜杆结构为中空碳纤维杆两端各用双头螺柱连接一球形螺母,在打印机运行过程中,由于温度变化不大,碳纤维杆变形较小[9-10],可认为斜杆长度基本不变,测量误差可控制在±0.1 mm之内,可近似认为该测量值与实际值吻合。于是微调的主要参数则为参数b。 4.1参数b的粗略调整 拟采用打印金字塔立方体试验(将于4.2节中说明)对参数b进行调整,首先应判断参数b的调节方向并粗略调整。此时引入抽纸法,具体做法为在调平的基础上,回零操作,热床上垫一张A4纸,用Pronterface软件控制Z轴下降至与A4纸接触且抽动A4纸略有阻力的位置,然后使打印头沿X轴或Y轴移动,一边移动一边抽动A4纸,感觉抽动用力的大小,由此判断路径。用力变小则说明打印路径为凹陷路径,需减小参数b;反之则为凸起路径,需增大参数b。 针对以上两种情况,首先应改变参数b的大小,不断重复上述操作以平缓路径的凹陷或凸起程度,直到打印头移动过程中抽动A4纸的力度不再明显变化,此时可进行打印金字塔立方体试验对参数b进行进一步微调。 4.2打印金字塔立方体试验 所谓金字塔立方体试验,是用打印机打印如图11所示模型。该模型由4层高度都为10 mm的长方体组成,每层的长宽分别为10×10、20×20、40×40、80×80,也可根据打印机尺寸具体设定。根据实际打印得到的模型每层长宽与要求值的差异,对参数b进行相应调整从而最终达到目标精度。 表2为对打印机进行调整时实际打印得到的数据。 表2金字塔打印数据记录表 参数c=216.9mm第一次打印第二次打印第三次打印 实际长度/mm实际宽度/mm实际长度/mm实际宽度/mm实际长度/mm实际宽度/mm10mm×10mm层10.2310.2210.0810.0810.0010.0020mm×20mm层20.5620.5420.1920.1820.0120.0140mm×40mm层41.2741.2340.4440.4240.0340.0380mm×80mm层82.7182.6381.0881.0380.0980.08最大误差+2.71+2.63+1.08+1.03+0.09+0.08 测量值调整后 调整后 参数b106.3106.0 105.8 对表格最大误差栏进行分析,可知第三次打印得到的模型误差最小,故采用参数b=105.8 mm。再将参数c分别取值216.8 mm和217 mm各进行一次金字塔立方体的打印,得到的模型最大误差均出现在80 mm×80 mm层,分别为(实际长度+0.13 mm,实际宽度+0.11 mm)和(实际长度+0.06 mm,实际宽度+0.05 mm),故采用参数c=217 mm。此时打印误差在可接受范围内,可认为参数调整完成,检验打印头在水平方面沿X轴或Y轴的移动应为一条水平线。 另有模型实际长度与实际宽度不相等的问题,原因在于打印机六根斜杆的实际长度不完全相等,而Marlin固件中只能设定一个参数c的值,由此引起某些斜杆计算曲线与运动曲线不吻合产生不同程度的打印缩放现象造成。此问题只能通过在装配过程中严格保证杆长相等来解决。 针对Kossel打印机构建过程中存在的微调困难的问题,本文通过建立数学模型的方法分析了打印机的运动原理、误差产生机理和影响因素,在此基础上结合具体实验对微调的两个方面——调平和调运动参数——提出了比较系统的调整方法。该方法的优点是调节快速、调节目标明确,并具有一定的通用性,对该类型3D打印机的快速构建和精度稳定性的提升具有指导意义。 [1]Jones R, Haufe P, Sells E, et al. RepRap - the replicating rapid prototyper.[J]. Robotica, 2011, 29(1):177-191. [2]Antonio Lanzotti, Domenico Maria Del Giudice, Antonio Lepore, et al. On the geometric accuracy of RepRap open-Source three-dimensional printer[J]. Journal of Mechanical Design, 2015, 137. [3]王冰, 彭斌彬. 并联机床结构分析[J]. 北华航天工业学院学报, 2006(5):8-11. [4]蔡睿妍.Arduino的原理及应用[J].电子设计工程, 2012(16):155-157. [5]刘欣灵.3D 打印机及其工作原理[J].网络与信息,2012(2):30 [6]Parth R. Kantaria1 Shyam. A Pankhaniya. Implementation of 3D Printer[J]. International Journal For Technological Research In Engineering, 2014, 1(9):819-822. [7]来永斌, 陈秀. 运用Excel辅助机械设计[J]. 机床与液压, 2004(12):179-180. [8]史厚强. 基于三点支承的仪器调平[C]// 第二届全国信息获取与处理学术会议,2004:824-826. [9]彭惠芬, 王程, 王鹏. 温度对碳纤维增强复合材料力学性能的影响[J]. 承德石油高等专科学校学报, 2014(3):12-15. [10]张凤翻,张雯婷.树脂基复合材料的上限工作温度[J]. 高科技纤维与应用. 2001(5) (编辑谭弘颖) 如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。 Research on influence factors and adjusting method of the accuracy of kossel 3D printer YUAN Zelin, FANG Hui, HUANG Jigang, ZHANG Wenjun, XIE Zhihao (College of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065, CHN) Kossel 3D Printer is a kind of parallel open source printer, has the advantages of fast printing, low noise, self replication, good expansibility. But in the process of assembly and using, adjustment is difficult, which has great influence on its performance and accuracy. Based on the analysis of the structure of Kossel printer, the paper studied the motion parameters of the firmware Marlin of Arduino controller, analyzed the factors of the accuracy of the printer, and carried out the adjustment method and the experimental verification, proposed an adjusting scheme, provided feasible technical support for further improving the printing accuracy. parallel 3D printer; Kossel; Marlin; Arduino; leveling; motion parameters TG659 A 袁泽林,男,1992年生,硕士研究生,研究方向为数控加工装备结构设计。 2015-11-10) 160408 *四川省科技支撑计划(2014GZ0122,2014GZX0001)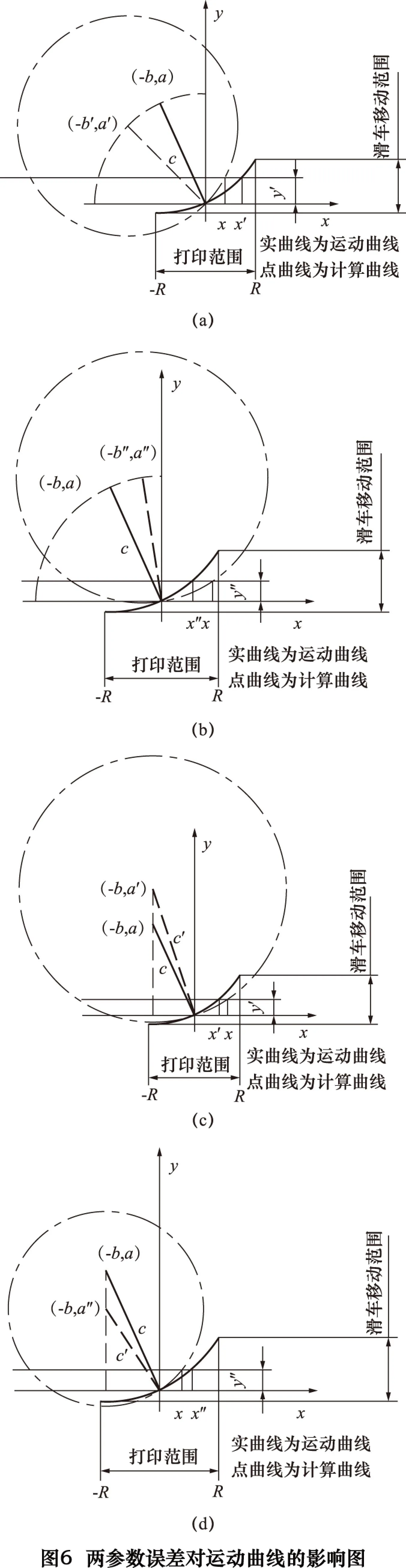

3 Kossel手动调平方案优选


4 Kossel运动参数调整实例


5 结语
