龙门加工中心滑鞍导轨布置形式研究及优化

赵坤坤　田亚峰　叶　霞

(①江苏理工学院机械工程学院，江苏 常州 213001；②常州昌隆机床制造有限公司，江苏 常州 213125)



龙门加工中心滑鞍导轨布置形式研究及优化

赵坤坤①田亚峰②叶霞①

(①江苏理工学院机械工程学院，江苏 常州 213001；②常州昌隆机床制造有限公司，江苏 常州 213125)

首先对滑鞍进行受力分析，然后通过有限元分析软件ANSYS Workbench对两种不同形式滑鞍进行静力学分析对比，最后采用拓扑优化和尺寸优化相结合的方法对龙门加工中心滑鞍进行优化设计。结果表明经过优化后的滑鞍质量减轻了227.8 kg，相比原结构质量减轻15.32%，最大变形量减小了0.241 6 μm，相比原结构最大变形量减小9.94%，同时动态特性略有提高，为滑鞍的优化设计提供了一种新思路。

龙门加工中心滑鞍；拓扑优化；灵敏度分析；尺寸优化

龙门加工中心是现代工业发展中必不可少的加工设备，滑鞍是龙门加工中心的重要部件之一，滑鞍与横梁导轨上的滑块通过螺钉固定在一起，主要受力为滑枕及其附属部件的重力以及切削力，滑鞍的主要作用为承载、定位和连接。滑鞍的静动态特性对龙门加工中心的加工精度和工件的加工质量都有很大影响，因此滑鞍的优化是机床优化设计的基础和关键。结构优化设计主要有尺寸优化、形状优化及拓扑优化。目前阶段国内对于机床结构一般还是采用经验设计，对滑鞍进行优化设计的很少。滑鞍结构主要有两种形式，即导轨平行布置形式和导轨垂直布置形式。本文在相同筋板结构及相同截面的情况之下，对这两种导轨布置形式的滑鞍进行静力学分析对比，然后用拓扑优化和尺寸优化相结合的方法对其进行优化设计，以期达到改善其动静态性能且减轻质量的效果。

1　滑鞍的有限元模型与受力分析

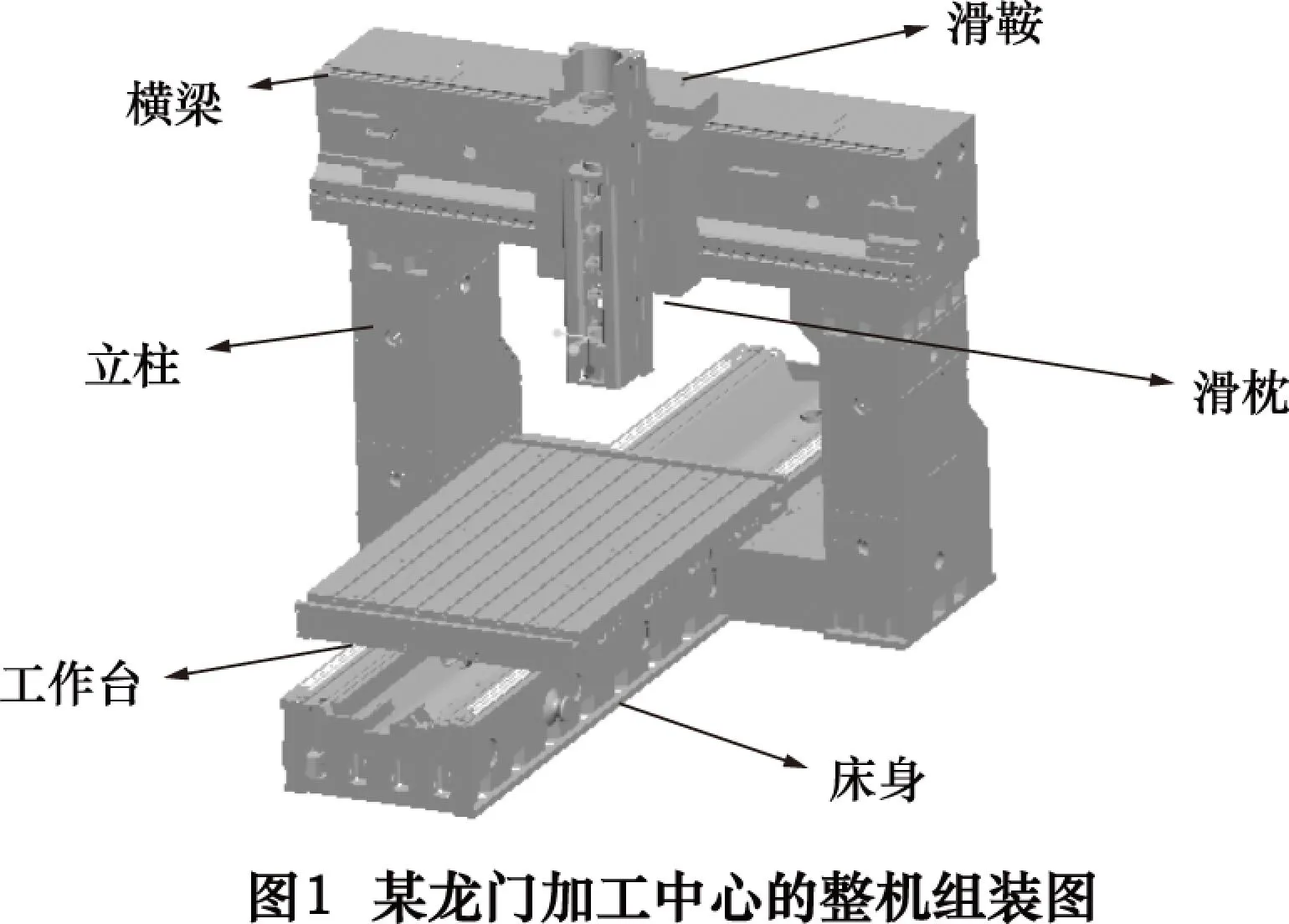
龙门加工中心主要由横梁、立柱、滑鞍、滑枕、工作台以及床身等部件组成，如图1所示。组装时横梁放在立柱上，滑鞍与横梁导轨上的导轨滑块通过螺钉固定在一起，滑枕及其附属部件安装在滑鞍上，滑鞍通过安装在横梁上的滚珠丝杠的转动带着滑枕及其附属部件在y方向的运动，滑鞍主要受力为滑枕及其附属部件的重力以及通过滑枕及其他附属部件间接作用的切削力。

使用三维软件Pro/E进行实体建模，并对滑鞍模型进行简化处理，忽略螺纹孔、圆角。倒角等特征。然后将模型导入有限元软件ANSYSWorkbench中进行分析，选择滑鞍材料为HT250，其弹性模量E=1.38×1011Pa，泊松比为0.156，密度ρ=7 280 kg/m3。

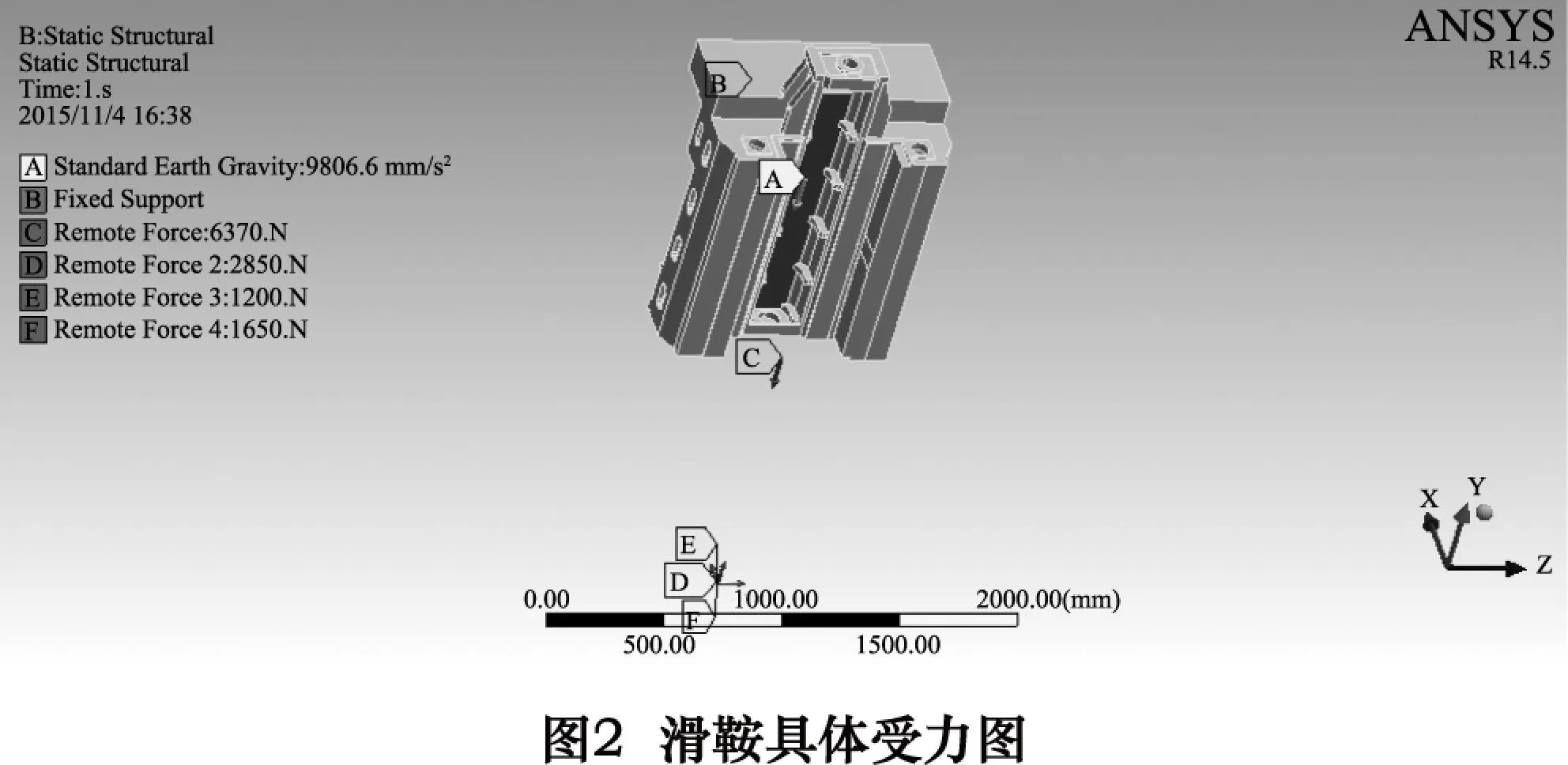
通过已有学者的研究可知，当滑枕、滑鞍及主轴部件运动至横梁中间位置，而滑枕运动到最低点时，横梁将会产生最大的弯曲变形[1]，而此时滑鞍亦处于极限位置，所以在此工况下对滑鞍进行分析。由于龙门加工中心设有的液压承载系统承受了滑枕及其附属部件的一半重力，故此时加载在滑鞍上的重力仅为其重力的一半，通过ANSYSWorkbench里面施加远端力(remote force)的方法进行加载，作用点为滑枕及其附属部件的重心位置[2]。在加工过程中切削力是不断变化的，因此只考虑极端工况下滑鞍承受的最大载荷。已知此时工件受到的最大切削力FC为3 000 N，则根据公式：

(1)

得到切削力在3个方向的分力分别为FX=2 850 N，FY=1 200 N，FZ=1 650 N。将这3个分力亦通过施加远端力(remote force)的方法进行加载。同时将滑鞍背部与横梁滑块相固定的两个面进行固定约束，并添加滑鞍自身重力，具体受力情况如图2所示。滑鞍的动态特性分析即滑鞍的模态分析，主要用于确定滑鞍的固有频率和振型，与其受载情况无关，因此在进行模态分析施加边界条件时，仅施加约束边界条件，不施加载荷边界条件[3]。

2　两种滑鞍的分析对比

在实际的龙门加工中心的生产中，比较常用的横梁导轨布置形式主要为两种，即导轨竖直方向平行布置形式以及导轨垂直布置形式。导轨竖直方向平行布置是指上、下导轨平行，而且都布置在横梁前侧；导轨垂直布置是指上、下导轨相互垂直，上导轨布置在横梁上侧，下导轨布置在横梁前侧[4]。滑鞍与横梁导轨上的导轨滑块通过螺钉固定在一起，所以滑鞍的主要形式也是两种，即导轨平行布置形式以及导轨垂直布置形式。由于两种滑鞍内部筋板结构以及截面基本相同，只是导轨的布置方式不同，因此这两种形式滑鞍的动态特性变化不大，所以只对这两种滑鞍进行静态特性分析对比。两种形式的滑鞍静态分析结果如图3，图4所示，对比结果如表1所示。

表1静力分析对比结果

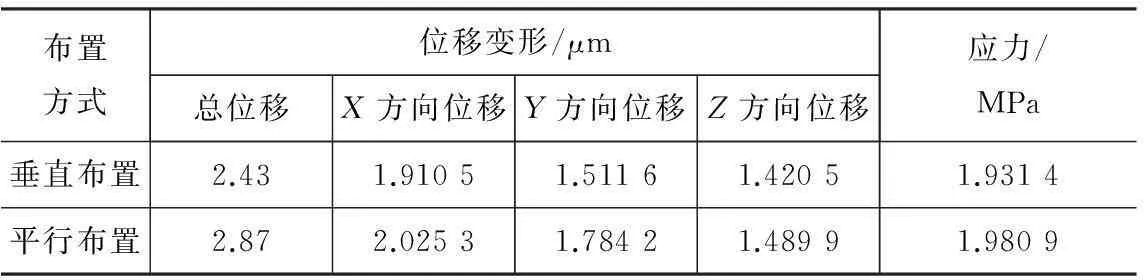
布置方式位移变形/μm总位移X方向位移Y方向位移Z方向位移应力/MPa垂直布置2.431.91051.51161.42051.9314平行布置2.872.02531.78421.48991.9809

通过滑鞍两种导轨布置形式的有限元分析对比结果可知，导轨垂直布置形式的各种变形量和应力都比导轨平行布置的要小，说明这种形式更加适合于滑枕只有部分镶嵌在滑鞍中的形式，虽然有液压承载系统承受了滑枕及其附属部件的一半重力，但是由于只有部分镶嵌造成力矩增大，因此滑枕及其附属部件作用在滑鞍上的重力依然很大，当采用导轨平行布置形式时由于滑枕及其附属部件所产生的重力与导轨受力相互垂直，会产生一个力矩造成变形量增大，而导轨垂直布置由于上侧导轨的受力方向和滑枕及其附属部件的重力相互平行所以不会产生力矩，因此导轨垂直布置形式在滑枕只有部分镶嵌在滑鞍中时有着更好的静态性能。接下来重点对导轨垂直布置形式滑鞍进行优化分析。

如图3所示，滑鞍最大变形发生在与丝杠连接的丝杠螺母处，最大变形量为2.429 5 μm。滑鞍的最大应力位置位于下侧导轨中部，最大应力大小为1.931 4 MPa，安全系数N=σb/σ1在20以上，其设计的安全系数较大[5]，说明滑鞍还有很大的优化空间。滑鞍的一阶固有频率为622 Hz，二阶固有频率为662 Hz。通过转速与频率的关系即n=60f求得一阶固有频率对应的转速为37 270 r/min，而本文中的龙门加工中心最大主轴转速为6 000 r/min，远远小于一阶固有频率转速，说明滑鞍的动态特性良好，完全可以避免共振。

3　滑鞍的拓扑优化分析

拓扑优化的主要思想是寻求结构的最优拓扑问题转化为在给定的设计区域内寻求最优材料的分布问题。在满足规定的减少材料量的同时满足结构最大化刚度的要求。拓扑优化的数学模型为：

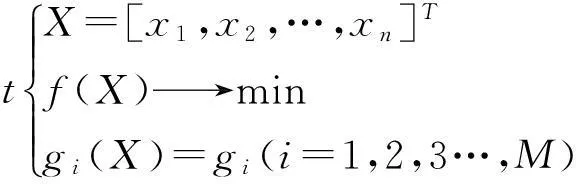
(2)

对滑鞍进行拓扑优化分析，利用有限元软件ANSYSWorkbench中的Shape Optimization功能，加上上文分析的边界条件，以减轻材料质量(target reduction)20%为目标进行拓扑优化，拓扑优化后的材料分布图如图5所示，图中灰色表示可以删除的部分，无色表示建议保留的部分。

从图中的拓扑优化结果中可以看到滑鞍上侧与滑鞍左下侧的材料是可以去除的。在保证滑鞍装配关系不改变的前提下根据滑鞍的变形云图、滑鞍一阶振型图和滑鞍最大应力云图发现滑鞍的左下侧材料对其动静态特性影响较大，所以选择去除滑鞍上侧的材料。同时考虑到滑鞍材料集中去除会导致其静刚度降低，需在空腔内适当的加入筋板以提高其刚度等性能[6]，因此选取3种常见的筋板单元，即#型、X型和米型对经过拓扑优化后的滑鞍的空腔进行填充。填充后的具体结构如图6所示。

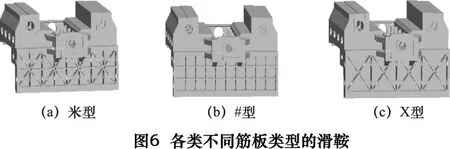
将这3种筋板模型加上相同的边界条件进行有限元分析，得到不同筋板类型滑鞍的静动态对比表(如表2所示)。

表2不同筋板类型滑鞍的静动态对比表

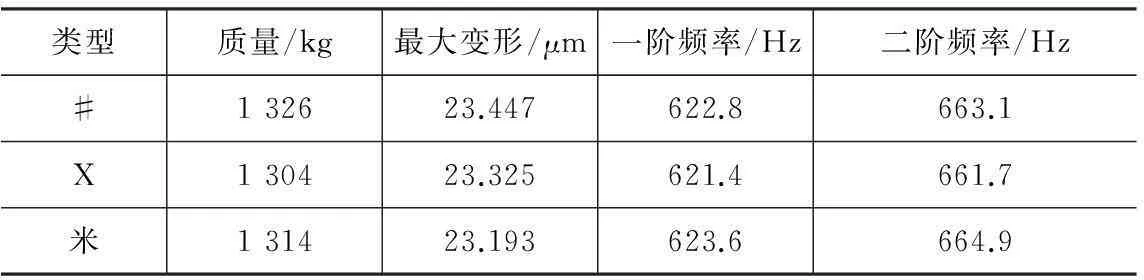
类型质量/kg最大变形/μm一阶频率/Hz二阶频率/Hz#132623.447622.8663.1X130423.325621.4661.7米131423.193623.6664.9

由表中可以看到这3种筋板类型各项数据差别均不是很大，其中X型筋板的质量最轻，同时最大变形量也不大，但其一阶和二阶频率较低，而#型筋板质量最重且变形量最大，所以综合考虑选择米字筋板对空腔进行填充，进行滑鞍尺寸优化分析。

4　滑鞍尺寸优化设计

尺寸优化是以结构尺寸作为优化设计变量，通过尺寸数值的反复迭代求解，寻求结构的最佳尺寸方案[7]。滑鞍的尺寸优化设计是指在传统经验设计得到的滑鞍结构的基础上，选择合适的尺寸参数，以滑鞍的静变形量和质量为性能指标，进行多目标联合灵敏度优化分析，得出各尺寸变量对滑鞍静变形量和质量的影响情况。然后根据灵敏度优化分析结果，使用有限元分析和响应面法相结合的方法确定滑鞍尺寸多目标优化函数，从而提高滑鞍的静动态特性。

4.1优化参数选择

在进行灵敏度分析时，选择的参数过多会使得计算量过大，造成资料浪费，参数较少则有可能漏掉对结构性能影响较大的尺寸参数。根据滑鞍的结构特点，选取侧边筋板厚度、背部筋板长度以及减重孔的直径等9个尺寸进行尺寸优化分析，如图7所示。各个变量的初始值和变化范围如表3所示。

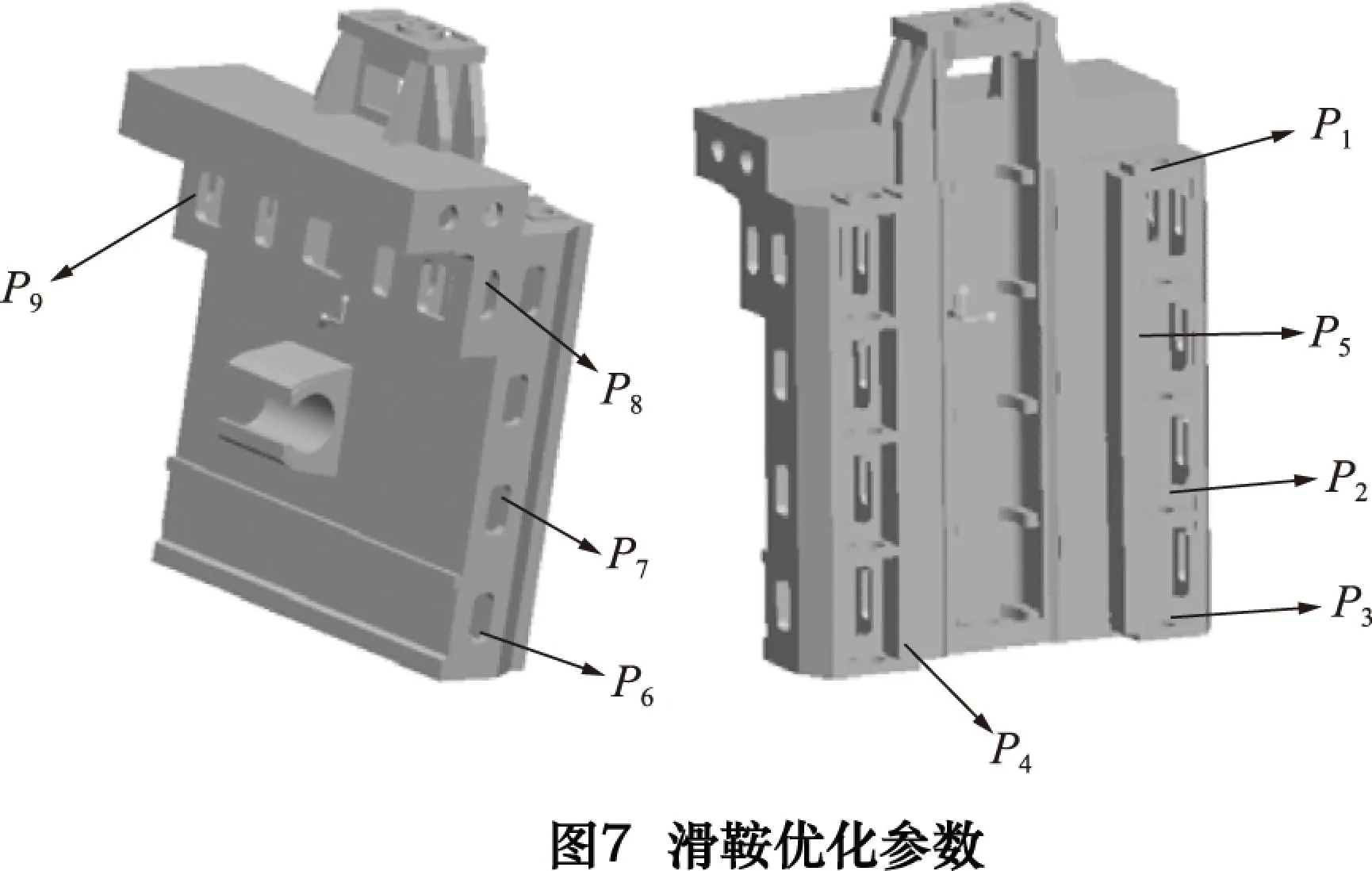
表3各个变量的初始值和变化范围

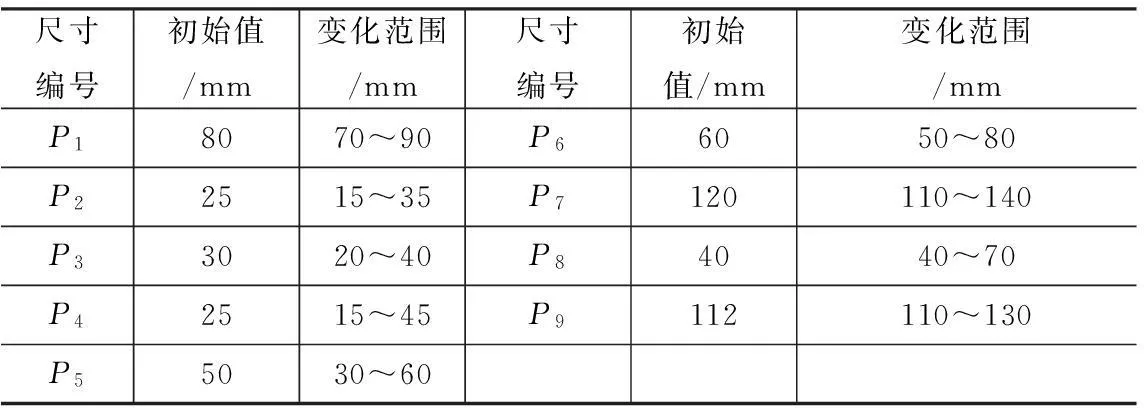
尺寸编号初始值/mm变化范围/mm尺寸编号初始值/mm变化范围/mmP18070～90P66050～80P22515～35P7120110～140P33020～40P84040～70P42515～45P9112110～130P55030～60

4.2灵敏度分析

结构的灵敏度分析是分析结构性能参数对结构设计参数变化的敏感性，灵敏度的数值可以反映结构各设计变量对结构性能的影响，灵敏度大表示该尺寸的微小改变将导致结构该性能的极大变化，灵敏度小则表示尺寸即使有较大的改变对结构该性能也不会有较大的影响[8]。

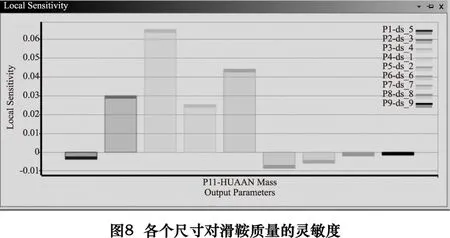
通过有限元分析得到各个尺寸对滑鞍的最大变形量和质量的灵敏度分析结果，从图8中看到P2、P3、P4和P5对质量影响较大。图9中可以看到P2、P4、P5和P7对最大变形量的影响较大。从中选择P2、P4、和P5进行进一步的分析。对于其他尺寸利用目标驱动优化(goal drive optimization，GDO)技术，采集设计参数样点，计算各个样点的响应结果，利用二次插值函数构造设计空间的响应面或者设计曲线，最终获得优化的解集[9]。

4.3基于响应面法的滑鞍多目标优化

正交实验设计是一种能够合理安排、科学分析各实验因素的一种研究多因素多水平的的数理统计方法。正交实验设计具有正交性，均衡分散性和综合可比的特性。将P2记为X1，P4记为X2，P5记为X3，X1X2X3即为正交试验的3因素，采用4水平3因素正交试验表进行正交试验。

为了减轻滑鞍质量同时又减小其最大变形量，需要对滑鞍进行多目标联合优化。响应面法是一种采用试验设计理论对指定的设计点集合进行试验，得到目标函数和约束函数的响应面模型，来预测非试验点响应值的方法[10]。在响应面分析中，首先要得到回归方程，然后通过对自变量的合理取值，能够在多目标优化中找到集中可行解中最优的设计点。二次响应面(多元二次多项式)的数学模型为：

(3)

根据正交实验结果，以X1、X2、X3作为自变量，滑鞍重量和最大变形量作为目标进行优化，通过MATLAB优化工具箱中的regress函数进行二次回归方程的拟合，得到滑鞍重量的拟合函数为；

Ym=1026+1.16X1+2.345X2+4.36X3

-0.014X1X2+0.000 3X2X3

+0.012X12-0.004X32

(4)

最大变形量的拟合函数为：

Ys=0.87+0.054X1-0.004X2+0.049X3

-0.000 3X1X2-0.000 5X1X3

-0.000 2X2X3-0.000 2X12

+0.000 2X22-0.000 4X32

(5)

对滑鞍进行多目标化优化设计的目的是减小其最大变形量并实现结构轻量化。这两个优化目标的重要性相同，因此取这两个优化目标函数的权重为相同值，即Km=Ks=0.5，从而将多目标优化转化为单目标优化。目标函数模型为：

(6)

利用MATLAB优化工具箱中的fmincon函数对目标函数进行求解，得到最优尺寸解为：

X1=30.42，X2=15.505，X3=46.471

经过圆整后的尺寸为P2=31 mm，P4=15 mm，P5=46 mm。

4.4优化后结果分析

将优化后的尺寸重新用三维软件Pro/E进行建模，加上相同的边界条件进行有限元分析，将优化前后的滑鞍静动态特性进行对比，对比结果如表4所示。

表4优化前后有限元结果对比

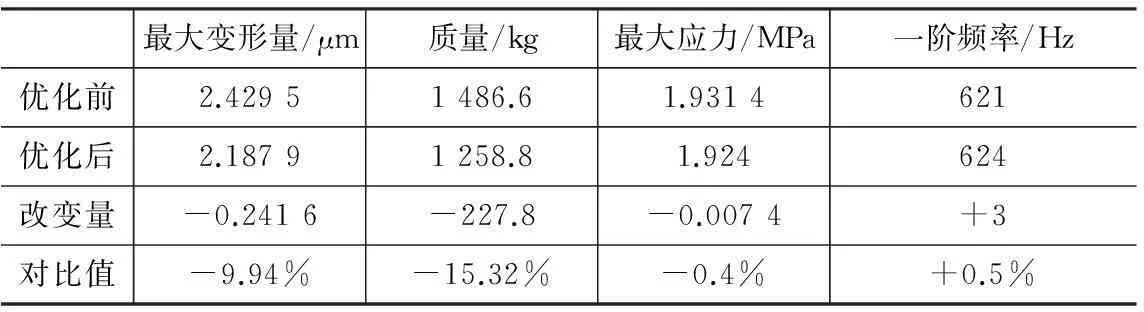
最大变形量/μm质量/kg最大应力/MPa一阶频率/Hz优化前2.42951486.61.9314621优化后2.18791258.81.924624改变量-0.2416-227.8-0.0074+3对比值-9.94%-15.32%-0.4%+0.5%

通过表中数据可见在施加相同的载荷边界条件和约束边界条件的情况下，经过优化后的滑鞍质量减轻了227.8 kg，相比原结构质量减轻15.32%，最大变形量减小了0.241 6 μm，相比原结构最大变形量减小9.94%，同时一阶固有频率略有提高。说明经过优化后滑鞍的动静态特性均得到了提高且质量降低明显。

5　结语

(1)通过两种滑鞍静力学分析可知导轨垂直布置形式在滑枕只有部分镶嵌在滑鞍中时有着更好的静态性能。通过模态分析可知滑鞍的动态特性良好，完全可以避免共振。

(2)使用拓扑优化分析能较精确地找出滑鞍的最佳材料分布和最优结构形式。然后根据拓扑优化结果同时结合工艺及其生产的具体要求进行设计，可以获得最好的设计结果。

(3)尺寸优化首先选择合适的尺寸参数，然后通过灵敏度分析找出各设计变量对滑鞍重量和最大变形量的影响程度，以影响最大的3个尺寸参数作为设计变量，综合考虑横梁的重量和最大变形量，利用响应面法构造回归方程，然后用matlab优化工具箱对滑鞍进行多目标优化求解，得到最优的尺寸参数。通过拓扑优化和尺寸优化滑鞍质量减轻了227.8 kg，相比原结构质量减轻15.32%，最大变形量减少了0.241 6 μm，相比原结构最大变形量减少9.94%，同时一阶固有频率略有提高。说明本文提出的滑鞍优化设计方法是合理可行的，同时也可以应用到机床其他零部件及整机的优化分析中。

[1]陈斯炮，李锻能，江涛，等.大跨距龙门五面体机床横梁最大工作载荷分析[J]. 机电工程技术，2009,38(9):89-92.

[2]陈艳，张松，陈舟，等. 龙门加工中心溜板动静态特性分析及优化[J].制造技术与机床,2014(8):64-73.

[3]张力．模态分析与实验[M]．北京：清华大学出版社，2011.

[4]李正羊，田亚峰，王礼明，等.龙门加工中心横梁导轨布置形式研究[J]. 组合机床与自动化加工技术,2015(2):65-69.

[5]陈庆堂.基于ANSYS的XK713数控铣床有限元分析及优化设计[D].南京:东南大学,2005.

[6]李珊珊,丛明,王贵飞，等.基于变密度法的床鞍结构拓扑优化设计[J].组合机床与自动化加工技术，2014(4)：19-25.

[7]杨玉萍,张森,季彬彬，等. 龙门加工中心横梁关键尺寸灵敏度分析与优化[J]. 制造业自动化，2013，35(8)：110-118.

[8]马迅，过学迅，赵幼平，等．基于有限元法的结构优化与灵敏度分析[J].机械科学与技术，2002，21(4)：558-561.

[9]刘成颖 ，谭峰，王立平.基于灵敏度度分析的机床床多目标优化研究[J].组合机床与自动化加工技术，2015(3)：1-4.

[10]Raymond H Myers.Response surface methodology current status and future direction[J].Journal of Quality Technology，1999,31(1)：35-40.

(编辑汪艺)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Optimization and the research on the forms of the sliding saddle arrangement of rails of gantry machining center

ZHAO Kunkun①, TIAN Yafeng②, YE Xia①

(①School of Mechanical Engineering, Jiangsu University of Technology, Changzhou 213001, CHN;(②Changzhou Changlong Machine Tool Manufacturing Co., Ltd., Changzhou 213125, CHN)

Firstly, the stress analysis is carried out, then the comparison of the static analysis of two different forms of sliding saddle are carried out by the finite element analysis software ANSYSWorkbench, the optimization design is carried out at last by using the method of topology optimization and size optimization. The result indicates that the quality of sliding saddle is reduced by 227.8kg after optimization and is reduced by 15.32% compared with the original structure. The maximum deformation is decreased by 0.241 6 μm and is decreased by 9.94% compared with the original structure, at the same time, the dynamic characteristics are increased slightly and provide a new idea for the design of sliding saddle.

saddle of the gantry machining center; topology optimization; sensitivity analysis; size optimization

TH123；TG502.31

A

赵坤坤，男，1989年生，在读硕士，研究方向为先进制造技术与装备。

2015-12-25)

160413