振动钻削用阶梯形变幅杆动力学性能仿真分析
2016-08-31李占国史尧臣
李占国 刘 丹 史尧臣
(①长春理工大学机电工程学院,吉林 长春 130022;②长春大学机械工程学院,吉林 长春130022)
振动钻削用阶梯形变幅杆动力学性能仿真分析
李占国①②刘丹①史尧臣①②
(①长春理工大学机电工程学院,吉林 长春 130022;②长春大学机械工程学院,吉林 长春130022)
阶梯形变幅杆具有结构简单、加工方便、放大倍数大等优点,但通过传统解析法所得变幅杆的实际谐振频率及节点位置与理论设计值存在较大偏差,后期需进行大量修整工作。以变幅杆截面突变处添加的过渡圆弧及杆长为修整目标,利用有限元方法分析了过渡圆弧及杆长变化对放大倍数、节点位置、谐振频率的影响规律,并得到满足设计要求时的修整量与原有结构参数之间的函数关系式。针对某振动钻削用阶梯形变幅杆,依据函数关系式求得其修整量,并对修整后的变幅杆进行分析。结果表明:沿法兰盘固定前后变幅杆性能参数与理论值均有较高的吻合度。
阶梯形变幅杆;有限元分析;影响规律;函数关系
超声振动钻削技术作为一种重要的特种加工方法,有效提高了深小孔钻削的加工精度及排屑能力。变幅杆作为超声振动系统的重要组成部件,主要用于振幅放大及换能器与声负载之间进行阻抗匹配[1]。常见的变幅杆有圆锥形、指数形、悬链形等。相对于其它形状变幅杆,阶梯形变幅杆以其结构简单、加工方便、放大倍数大等优点受到广泛应用[2]。变幅杆设计时要求其性能参数满足理论设计要求,且法兰盘固定前后无明显变化。即变幅杆在实现固定的同时降低了因振动抑制而造成的能量损耗,从而保证超声能量的有效传递。但由于传统解析法所得阶梯形变幅杆的实际节点位置及谐振频率与理论设计值存在较大偏差,后期往往需要进行大量修整工作,使设计过程变得繁琐[3-4]。
本文针对阶梯形变幅杆,运用有限元方法分析了过渡圆弧及杆长变化对放大倍数、节点位置、谐振频率的影响规律,并得到了相应函数关系式,从而简化修整过程,有效地提高了变幅杆的设计效率。
1 阶梯形变幅杆的理论设计
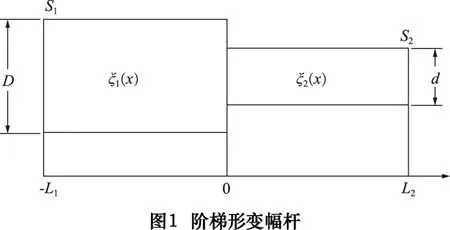
阶梯形变幅杆结构如图1所示,由两段不同半径的等截面圆杆组成,其中大段直径为D,截面积为S1,长度为L1;小段直径为d,截面积为S2,长度为L2。由于超声波在变截面杆中的传播可看做简谐振动,则阶梯形变幅杆纵振波动方程为:
(1)
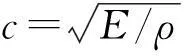
由式(1)求解得到质点位移方程:
ξ1(x)=A1cos(kx)+B1sin(kx)(-L1≤x≤0)
(2)
ξ2(x)=A2cos(kx)+B2sin(kx)(0≤x≤L2)
(3)
结合两端自由时的边界条件,可求得阶梯形变幅杆的频率方程、放大倍数MP、位移节点x0分别为:
S1tan(kL1)+S2tan(kL2)=0
(4)
MP=(S1sin(kL1))/(S2sin(kL2))
(5)
x0=L2-λ/4
(6)
式中:λ=c/f为纵波波长。根据式(5)、(6)求解可知,当大小段杆长均为四分之一波长时,变幅杆放大倍数达到最大,此时节点位于变幅杆的中间位置,即截面突变处。
本文针对某振动钻削用阶梯变幅杆进行设计,其理论谐振频率f=30 kHz,材料为45钢,材料参数如表1所示,大段直径D=34.2 mm,小段直径d=13.7 mm。则通过理论计算可得变幅杆大小段杆长L1=L2=L=λ/4=85.6 mm、径长比α=D/L=0.4、大小段直径比N=D/d=2.5、放大倍数Mp=N2=6.25。
表145钢的材料参数

材料密度ρ/(kg/m3)弹性模量E/GPa声速c/(m/s)泊松比μ45钢7850207.151360.28
2 阶梯形变幅杆有限元分析
运用CATIA建立上述解析法所得阶梯形变幅杆的三维模型,将其导入ANSYS软件,材料属性根据表1定义,然后进行模态分析,得到变幅杆纵振模态下过轴线任意截面的位移分布云图如图2所示,并将其性能参数的仿真结果与理论值对比列于表2。
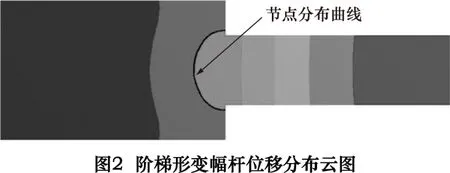
表2阶梯形变幅杆性能参数对比

x0/mmf/HzMP理论值0300006.25仿真值-7.3275915.91
从所得结果可以看出,变幅杆谐振频率仿真值远低于理论谐振频率;轴心节点位置向大段偏移,且过轴线任意平面内的节点分布是一条近似圆弧的不规则曲线。这是因为传统解析法忽略了变幅杆纵振过程中截面突变处应力集中及材料的横向振动。因传统解析法通常将变幅杆的轴心节点视为固定节点并向外延伸设置法兰盘进行固定,这样势必会抑制变幅杆的振动甚至造成损坏[5-6]。
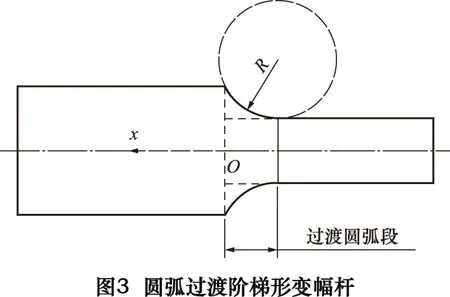
对解析法所得阶梯形变幅杆进行修整时,为减小截面突变处应力集中对变幅杆谐振频率的影响,往往在截面突变处添加过渡圆弧。当圆弧半径小于大小段半径差时,圆弧与突变截面及小段均相切;当圆弧半径大于大小段半径差时,添加方法如图3所示,一端与变幅杆大段边缘相交,另一端与变幅杆小段相切。法兰盘的添加位置应选在变幅杆轴向外缘轮廓上振动位移为零的位置,即轮廓节点处。
3 阶梯形变幅杆性能影响规律分析
由于变幅杆的大小段直径需根据换能器及钻削加工刀具系统尺寸确定,其修整一般只针对截面突变处的过渡圆弧及杆长[7]。因此本文针对振动钻削用变幅杆,系统研究了不同N、α、f时过渡圆弧及杆长变化对变幅杆性能参数的影响规律。
3.1过渡圆弧对性能影响规律分析
取f=20 kHz、α=0.3,当N分别等于2、3、4时,对不同过渡圆弧的阶梯形变幅杆进行有限元分析,得到过渡圆弧半径R对变幅杆性能的影响规律如图4所示。
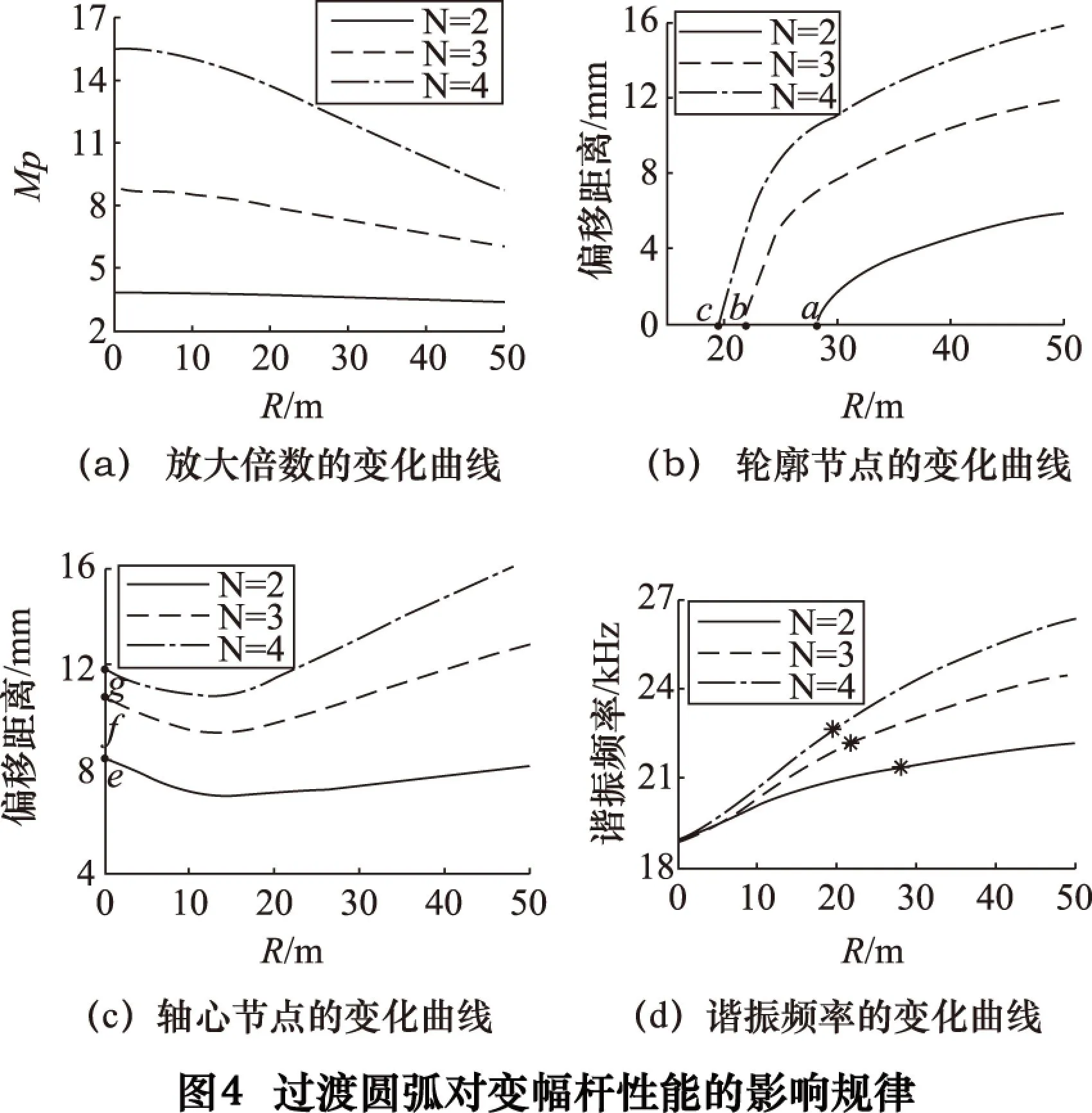
由图4a和4b可以看出,随R增大,变幅杆的放大倍数逐渐减小;轮廓节点沿过渡圆弧段向大段方向产生偏移,并且当R增大到某一值(a、b、c)时,轮廓节点移动到大段与过渡圆弧段交界处。由于变幅杆在轮廓节点位置需设置法兰盘,而过渡圆弧段应力、应变分布比较复杂[8],且考虑到此处法兰盘加工难度等问题,轮廓节点分布于过渡圆弧段显然是不合理的。综合考虑,轮廓节点应位于大段与过渡圆弧段交界处,此时的过渡圆弧称之为理想过渡圆弧,其半径用RL表示。
对比图4b和4c中变幅杆轮廓节点及轴心节点位置的变化情况可以看出,随N值变化,RL(a、b、c)与无过渡圆弧时轴心节点的偏移距离x(e、f、g)在数值上存在相同变化规律。
首先对无过渡圆弧的阶梯形变幅杆进行有限元分析,得到x随N、α、f的变化规律如图5所示。
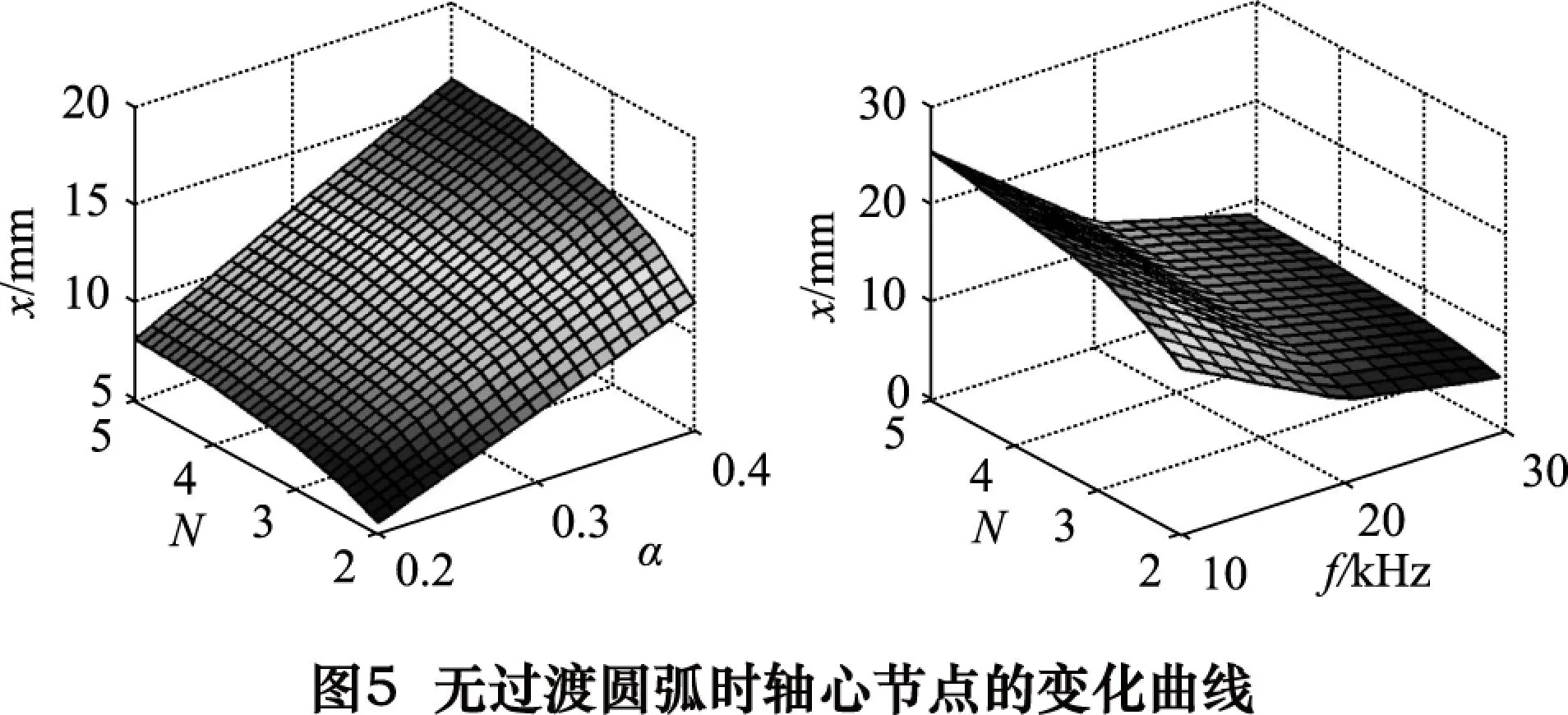
从图5可以看出,x随N增大而增大,增大幅度逐渐减小;与α近似于正比例关系;与f近似成反比。经整理,可将x与N、α、f间的关系可表述为:

(7)
通过分析RL与无过渡圆弧时过轴线任意平面内轴心节点及截面突变处大段两端点组成圆弧的半径之比y的变化规律,所得结果如图6所示。
通过上述分析可得RL与x之间的关系,整理后可将RL与N、α、f之间的关系可表述为:
(8)
通过图4d分析可知,变幅杆的谐振频率随R增大逐渐增大。如图中标记点所示,当R=RL时阶梯形变幅杆的谐振频率均大于理论谐振频率f。经分析,添加理想过渡圆弧后的变幅杆谐振频率相对于f的增量Δf与f的百分比变化规律如图7所示。
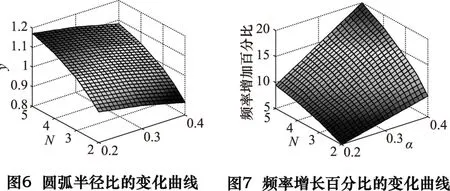
通过上述分析可将Δf与N、α、f之间的关系表述为:
Δf=[-(0.162 2-0.315α)N4+(2.078 3-3.48α)N3
-(9.387-10.68α)N2+(16.87+8α)N
-(9.39+15.6α)]f/100
(9)
3.2杆长对性能影响规律分析
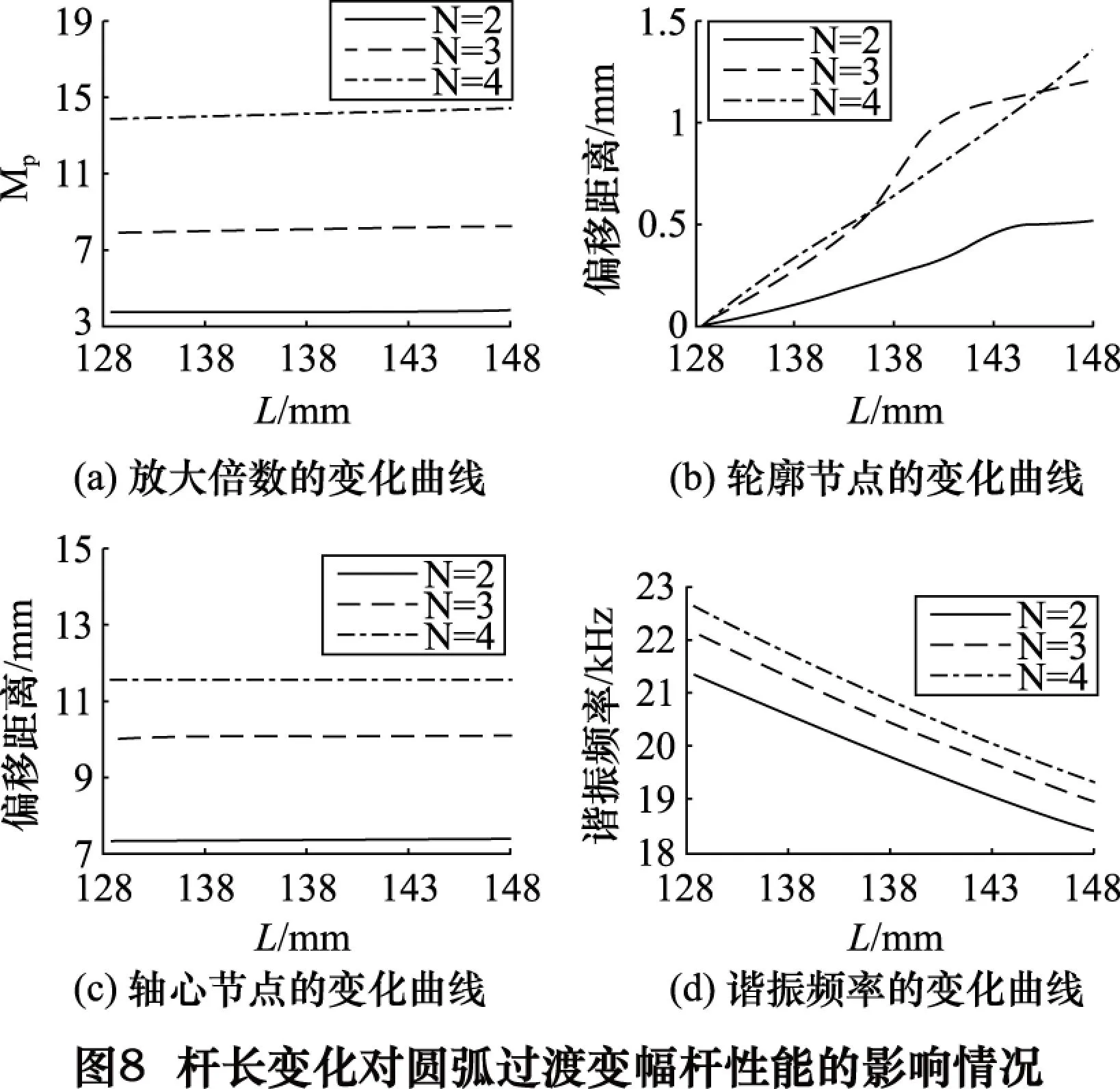
在添加理想过渡圆弧情况下,对f=20 kHz、α=0.3、N分别等于2、3、4时的阶梯形变幅杆进行有限元分析,得到杆长变化对变幅杆性能的影响情况如图8所示。其中杆长变化是指变幅杆两端同时增加或减小某一长度。
根据图8分析可知,随杆长增加,变幅杆放大倍数、轮廓节点及轴心节点向大段方向的偏移量均有较小变化;谐振频率明显减小。为使具有理想过渡圆弧阶梯形变幅杆的谐振频率接近理论谐振频率f,可适当调整变幅杆的杆长[7]。
针对具有理想过渡圆弧的阶梯形变幅杆,将其大小段杆长同时增加或减小1 mm时所产生的频率变化量与f的百分比δ定义为杆长变化对谐振频率的影响系数。通过分析得知,频率影响系数δ对N及α的敏感度相当低。在忽略两者影响的前提下,得到δ随f的变化规律如图9所示。
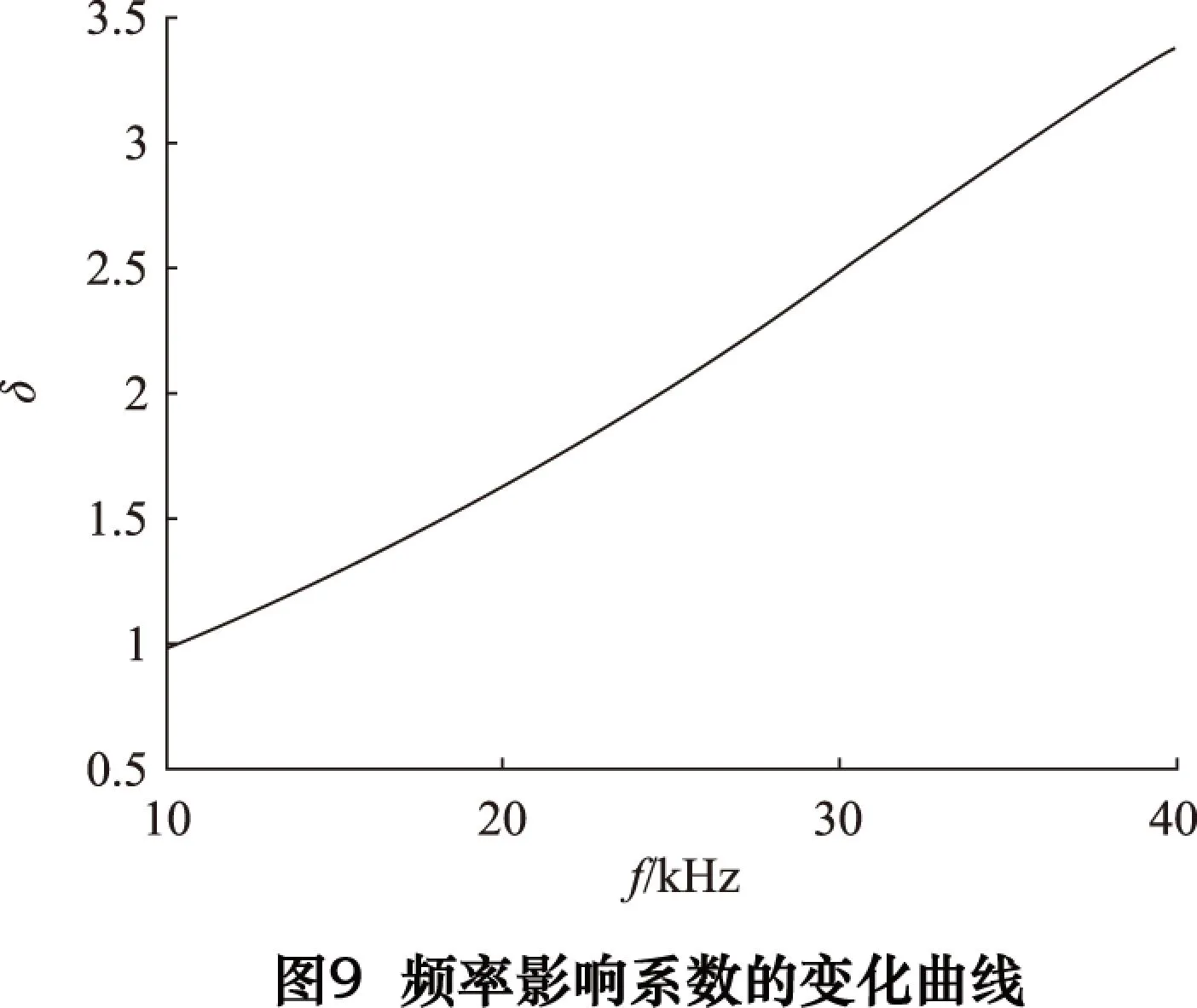
对图9所示规律进行分析整理,得到δ与f之间的关系式为:
δ=-0.000 001 631(f/1 000)4+0.000 136 7(f/1 000)3
(10)
通过式(10)求出杆长对谐振频率的影响系数δ,结合式(9)可得到修整后变幅杆的实际杆长:
LS=L+200Δf/(fδ)
(11)
由于变幅杆轮廓节点的位置随杆长变化会产生微量偏移,但通过分析发现,满足谐振频率要求的杆长增量使轮廓节点沿轴向产生的偏移范围内,变幅杆外缘纵振幅值与大段端面纵振幅值相差至少两个数量级,故杆长变化对节点位置的影响可以忽略。
4 验证
依据上述分析对第一节理论设计所得阶梯形变幅杆进行修整,修整后的变幅杆杆长为95.16 mm,过渡圆弧半径为22.9 mm,并在大段与过渡圆弧段交界处添加同样大小的法兰盘。对法兰盘固定前后的变幅杆进行分析对比,对比结果如表3所示,通过传统解析法所得变幅杆,沿法兰盘固定前后其谐振频率与理论值之间的偏差均比较大,放大倍数在固定前与理论值较接近,但法兰盘固定前后变化较大;而修整后的变幅杆,沿法兰盘固定前后其谐振频率均接近于理论值,固定前后放大倍数变化小于6%。
表3变幅杆性能参数对比
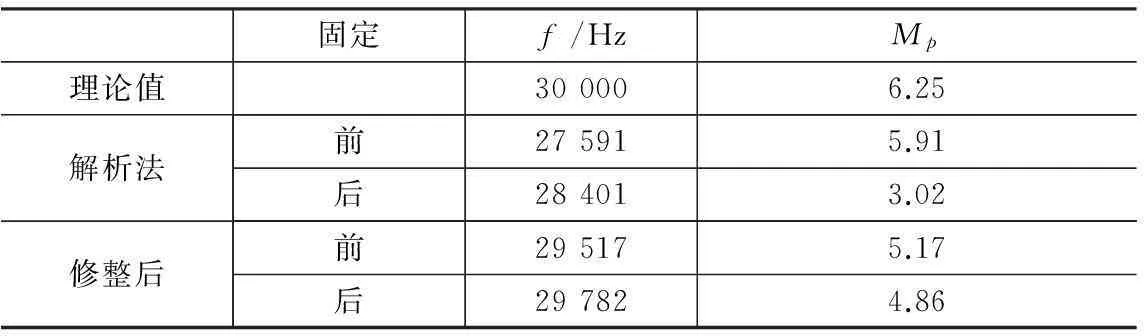
固定f/HzMp理论值300006.25解析法前275915.91后284013.02修整后前295175.17后297824.86
5 结语
(1)分析了阶梯形变幅杆过渡圆弧对其放大倍数、节点位置、谐振频率的影响规律,并得到使轮廓节点位于变幅杆大段与圆弧过渡段交界处时的理想过渡圆弧半径RL与N、α、f之间的函数关系。
(2)分析了具有理想过渡圆弧阶梯形变幅杆杆长对其放大倍数、节点位置、谐振频率的影响规律,并得到满足谐振频率时杆长Ls与N、α、f之间的函数关系。
(3)针对某阶梯形变幅杆,对比修整前后变幅杆性能参数,可以看出修整后的变幅杆沿法兰盘固定前后的性能参数均接近理论值,较好地满足了设计要求,有效地提高了变幅杆的设计效率。
[1]林仲茂. 超声变幅杆的原理和设计[M].北京:科学出版社, 1987:53-54
[2]贾杨,沈建中. 带过渡圆弧阶梯形变幅杆的有限元分析[J]. 声学技术,2006,25(1):75-81
[3]赵波,许永强,郑友益,等. 基于ANSYS的超声变幅杆节点优化及振动性能试验[J]. 河南理工大学学报,2014,33(3):304-308
[4]Graham G,Petzing J N,Lucas M.Modal analysis of ultrasonic block horns by ESPI[J]. Ultrasoics, 1999(37) : 149-157.
[5]赵明利,程雪利,赵波. 带工具头超声变幅杆节点定位偏差问题分析[J]. 声学技术,2013,32(3):253-256
[6]陈俊波. 超声变幅杆节点优化设计[J].声学与电子工程,2009,95(3):23-25
[7]郑建新,侯雅丽. 阶梯形变幅杆数值设计研究[J]. 机械设计,2015,32(5):91-94
[8]曾凡凡,王时英,吕明. 阶梯形变幅杆圆弧过渡动力学分析[J]. 机械设计与制造,2012,10(10):210-212
如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。
Dynamic performance analysis for vibration drilling with stepped horn
LI Zanguo①②,LIU Dan①,SHI Yaochen①②
(①College of Mechanical and Electrical Engineering, Changchun University of Science and Technology,Changchun 130022, CHN; ②College of Mechanical Engineering, Changchun University, Changchun 130022, CHN)
Stepped horn has the advantages of simple structure, easy processing, high magnification and so on, but traditional analytical method of the results and theoretical design value has relatively large deviation, there are large number of repair work need by later process. Taking the transition arc and the rod length as the trimming target, the influence law of the transition arc and the length of the rod to amplification factor, node position, resonance frequency is analyzed by the finite element method, and the functional relationship between the amount of repair and the original structural parameters is obtained. Aiming at the stepped horn used in vibration drilling, the change of the amplitude of the horn is obtained according to the function relation, and analyze the trimmed horn by finite element analysis method. The results show that the amplitude transformer performance parameters are in good agreement with the theoretical values.
stepped horn; finite element analysis; influence law; function relation
TB559
A
李占国,男,1961年生,教授,博导,研究方向为现代机械设计理论与方法,已在国内外发表论文40余篇。
(编辑李静)(2015-11-30)
160412
