CVD涂层刀具高速铣削大理石切削力研究*
2016-08-31闫海鹏吴玉厚宗宇鹏
闫海鹏 吴玉厚 宗宇鹏
(沈阳建筑大学机械工程学院,辽宁 沈阳 110168)
CVD涂层刀具高速铣削大理石切削力研究*
闫海鹏吴玉厚宗宇鹏
(沈阳建筑大学机械工程学院,辽宁 沈阳 110168)
选定切削参数(切削速度、进给速度、切削深度)设计正交试验,进行CVD氮化钛涂层刀具高速铣削大理石切削力试验,利用测力仪测出各组试验的切削力信号图,分析信号图特征得出切削力值,并记录各组切削力试验结果。分析单一切削参数(切削速度、进给速度,切削深度)对切削力变化的影响规律。采用最小二乘法原理对切削力经验公式回归系数进行参数估计,并对经验公式进行相关性检验,检验结果表明显著性很高。最终通过试验结果得出:切削力随着进给速度和切削深度的增加而增大,随着切削速度的增加而减小;并且切削深度对切削力影响最大,切削速度次之,进给速度对切削力的影响最小。
CVD涂层刀具;大理石;切削力;切削参数;最小二乘法
天然大理石——汉白玉具有耐磨性好、硬度高、强度高等特点,被广泛应用于建筑行业等领域,但是该材料的韧性比较差,切除过程与金属材料的切除过程有所不同,其切削层的切除是通过断裂破碎而成为切屑的,因此,在稳定铣削阶段切削力变化并不稳定[1]。
作为高速铣削天然大理石机理的研究重点之一,切削力的测量、切削力数值的处理并不是一个简单的过程,切削过程中机床的振动、刀具的磨损以及切削热的变化等都会影响到切削力的变化,因此基于现场真实数据的统计回归数学模型则成为准确性较好的高速切削力研究方法[2-5]。在高速铣削条件下,研究切削参数对切削力变化规律的影响,对于改善大理石表面加工质量,延长刀具使用寿命等有重大意义[6-8]。
文献[2]比较分析了PCBN和陶瓷刀具对淬硬模具钢Crl2MoV高速切削时切削力的变化规律,得出了采用PCBN刀具切削时拥有较小的切削力。文献[7]利用神经网络建立AlTiN涂层硬质合金立铣刀加工4Cr5MoSiV1钢时影响切削力变化模型,并用网络预测结果与实际数据比较分析了切削力的变化规律。
本文通过CVD氮化钛涂层刀具高速铣削大理石试验,研究切削力随着切削参数(切削速度、进给速度、切削深度)的变化规律,详细分析了各切削参数对切削力变化规律的影响,建立了切削力与切削参数之间的数学预测模型,并对预测模型进行显著性检验。
1 切削试验
1.1试验工件的选择
本试验使用的工件材料为天然大理石——汉白玉,是目前应用较为广泛的一种天然大理石,如图1所示。汉白玉的主要成分是碳酸钙,它是一种化合物,化学式是CaCO3。汉白玉基本上不溶于水。汉白玉可以存在于以下形态:方解石、霰石、石灰岩、白垩、大理石、石灰石,也可于岩石内找到。同时也是动物贝壳和蜗牛壳的主要成分。它还是重要的建筑材料,汉白玉的质地坚硬洁白,石体中泛出淡淡的水印,俗称汗线,故而得名汉白玉。

试验所采用的汉白玉大理石吸水率为0.16%、体积密度为2 800 kg/m3、抗弯强度为10.3 MPa、抗压强度为1 072 MPa,冷却方式选择外部水冷。
1.2试验设备
机床:异型石材车铣加工中心,如图2所示。主要针对当前石材制品向着精品化、异型化方向发展的趋势,特别是针对国内在三维雕塑制品和回转体异型石材制品方面的技术空白而研制。该异型石材车铣复合加工中心为八轴五联动数控机床,配有立式和卧式两个工作台,车削和铣削两个独立的工作头。由两个复合工作头和两个工作台组成了两套八轴五联动系统。本文实验用的五轴系统是卧式工作台旋转分度(A轴),横梁Y轴向进给、滑鞍Z轴向进给、高速雕铣工作头X轴进给和绕B轴旋转分度,为标准的摆头转台正交五轴机床。
测力仪:瑞士Kistler公司生产的9257B型三向压电式测力仪,如图3所示。包括:电荷放大器、数据分析系统、数据采集装置、三向测力仪。
试验刀具:试验使用的刀具为D6CVD球头铣刀如图4所示,其主要参数如表1所示。



表1试验刀具主要参数

基体材质涂层材料维氏硬度涂层厚度规格钨钢TiNTiCN103μmR3.0×L50
1.3试验方案
正交试验设计是分析多因素多水平的一种研究方法[9-10],它是根据正交性从全面试验中整理出部分有代表性的点进行试验,这些有代表性的点具有了“均匀分散,齐整可比”的特性,正交试验设计是分式析因研究的首选方法。试验选用L16(43)正交表来进行,如表2所示。此表以进给速度、切削速度、切削深度作为3个因素,每个因素选择了4个水平,根据CVD涂层刀具的耐磨性能以及加工中心的功率,综合考虑选择切削速度vc=38、76、114、152 m/min,切削深度ap=1、2、3、4 mm,进给速度vf=1 000、2 000、3 000、4 000 mm/min,总共16组试验。
将天然大理石试件固定在测力仪上,如图5所示,将编制好的NC代码输入到数控机床中,进行大理石切削试验,保存好切削力信号。切削力测量结果如表2所示。
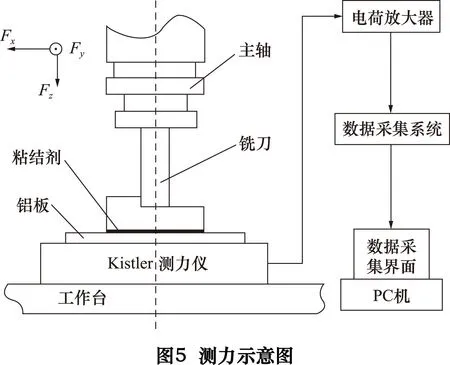
表2切削力测量结果

序号切削速度vc/(m/min)进给速度vf/(mm/min)切削深度ap/mmFx/NFy/NFz/N1381000128.6036.7475.192382000258.1688.52175.913383000385.08128.57262.4343840004122.85144.46290.035761000239.2248.2795.586762000123.3327.7060.957763000493.33137.62281.468764000380.56120.17230.4491141000349.0578.41144.03101142000475.84108.13221.41111143000124.7330.3564.72121144000240.1955.68108.85131521000469.2899.24198.43141522000347.2367.56135.64151523000235.0241.9788.29161524000126.0632.3169.41
2 试验结果分析
2.1高速铣削天然大理石切削力分析
图6为本次试验的切削力信号图,在点A之前为刀具没有接触工件时的空切阶段,此时的切削力不为零且有细微波动,说明测力仪的调节没有完全抑制零漂,机床在切削工件前本身还有一定的振动,但是振动不大,不影响正常试验及切削力的测量;A点之后为刀具接触工件到稳定切削的动态过程,切削力信号线上下大幅度波动,这是由于大理石为硬脆性材料,切屑类型以崩碎切屑为主,切削刃刚与工件接触到将切屑切除这阶段是切削力迅速增大,切削力信号表现为从波谷上升到波峰;当刀具前方材料被切下后,刀具发生局部空切,切削力迅速减小,切削力信号表现为从波峰下降到波谷,刀具继续进给,以上两个过程交替循环发生,直至切削层被完全切除;B点为刀具完成切削离开工件,取切削力信号图相邻波峰与波谷的差值的平均值作为切削力的值,称为静态切削力。
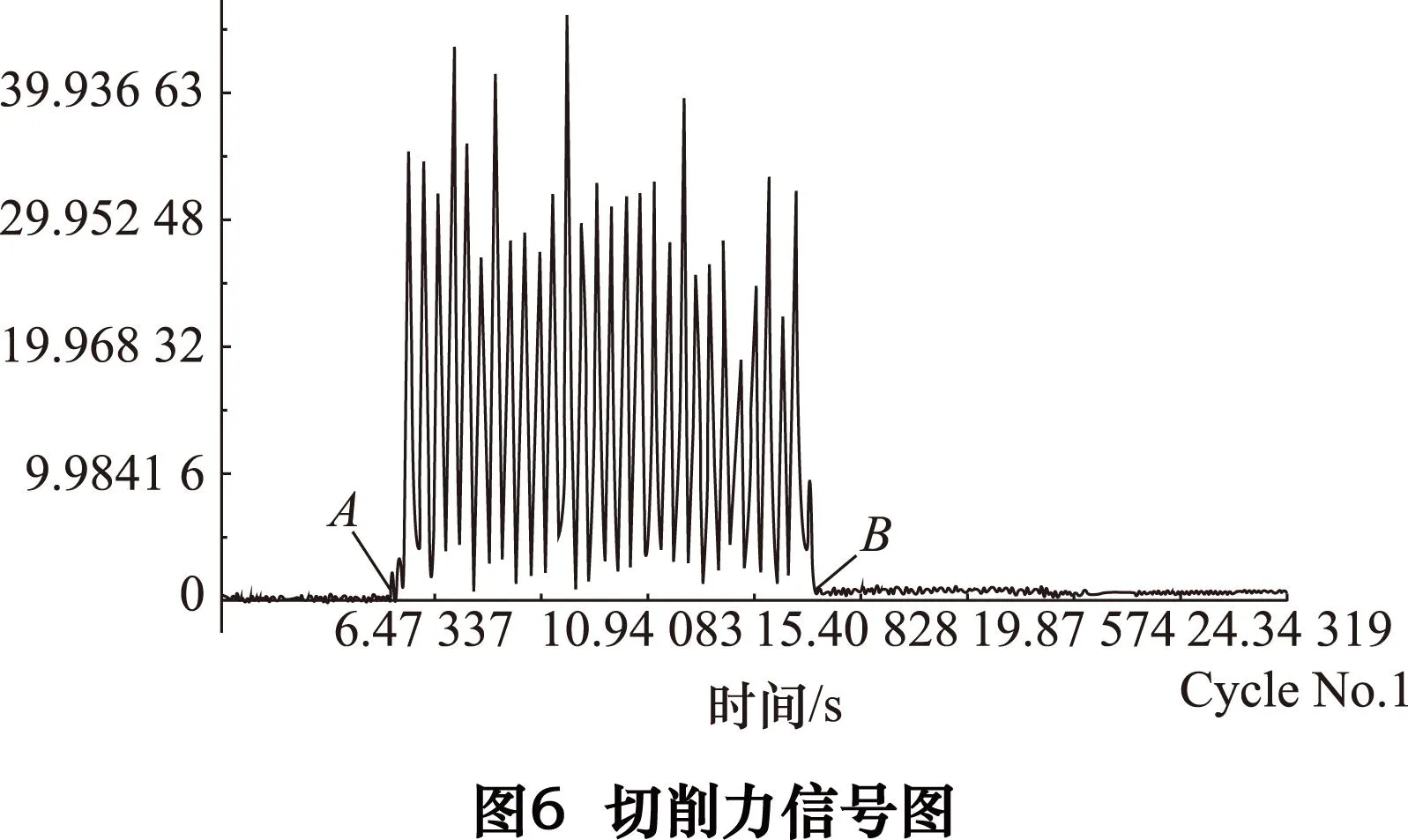
2.2切削参数对切削力的影响规律
如图7所示,Fx、Fy、Fz分别表示进给力、背向力、主切削力,从图中可以看出,Fz的值明显大于Fx和Fy的值,这是由于主运动消耗的功率最多。切削速度增加,Fx、Fy、Fz几乎呈线性减小趋势,这是因为切削速度的提高,切削温度上升,一方面,减小了工件与刀具之间的摩擦系数,另一方面降低了工件的剪切强度和硬度,最终致使切削力减小。在切削速度达到114 m/min时,由于大理石粉末覆盖在切削刃上,导致刀具锋利程度下降,所以切削力减小趋势变缓慢。
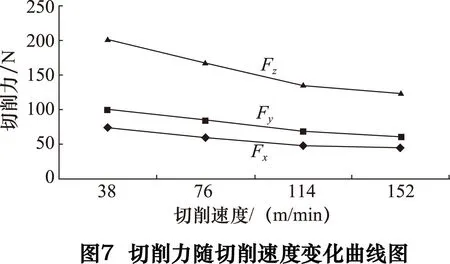
图8为切削力随进给速度变化曲线图,由图可知随着进给速度的增加,切削力呈增大趋势,这是由式AC=f×ap可知:在切削深度ap恒定的前提下,伴随进给量f的增加,切削面积AC呈线性增大,致使材料在单位时间内被去除体积增加,亟需的能量增大,因此切削力增大;在进给速度为3 000~4 000 mm/min时,切削力增大趋势变缓,这是由于刀具与工件相对运动,切削后的表面存在材料残留,被称为残留面积,又因为由残留面积高度理论公式Rmax=f2/8rξ可知,随着进给量f的提高,增加了残留高度,致使切削力增大速度缓慢。

由图9可知,切削力随切削深度的增大而增大,原因如上述,在进给量恒定的前提下,随着切削深度的增加,切削面积呈线性增加的趋势,致使材料在单位时间内被去除体积增加,亟需的能量增大,因此切削力增大。

2.3切削力经验公式回归模型的建立
为了更好地指导生产实际,有必要建立起切削力与各影响因素之间的内在联系。假定切削力F是3个独立变量(切削速度、进给速度、切削深度)的指数函数,公式如下所示[11]:
(1)
式中:b1、b2、b3分别是各自独立变量的相关系数;是与工件材料、刀具材料、切削条件等相关的系数。
为了使经验公式方便计算,将式(1)两端取对数,将指数函数变为线性函数,则:
lnF=lnk+b1lnvc+b2lnvf+b3lnap
(2)
令b0=lnk,x1=lnvc,x2=lnvf,x3=lnap,y=lnF,并代入式(2)得:
y=b0+b1x1+b2x2+b3x3
(3)
(4)
上式为线性回归方程,即自变量x1、x2、x3与因素y之间存在线性关系。本次试验数据如表2所示,共有16组数据,分别带入式(4),可得到如下方程组:
Y=XB+ε
(5)
其中ε=(ε1,ε2,ε3,…,ε16)T为误差矩阵。
采用最小二乘法原理对预测模型的回归系数进行参数估计,则:
B=(XTX)-1XTY
(6)
式中:X为独立变量矩阵;B为回归系数的参数估计;Y为切削力的矩阵。将矩阵的数值输入Matlab软件进行计算,分别得到如下结果:
(7)
(8)
(9)
根据以上3个算式,很容易看出:切削深度是对切削力影响最大的因素;切削速度次之;进给速度对切削力的影响最小。
2.4经验公式的检验
虽然切削力经验公式有一定根据,但只是一种假设,建立之前并不能确立其关系的正确性,因此需要进行相关检验。
为了精确地进行检验,试验值yi与按公式预测值Yi不可能完全一致,即试验点(xi,yi)并不能完全落在经验公式的函数曲线上,各试验点偏离曲线的程度,可用它们的总偏差来表征,y是各试验yi的平均值,将总偏差平方和ST分解为残差平方和SE和回归平方和SA,计算公式如下:
ST=∑i(yi-y)2
(10)
SE=∑i(yi-Yi)2
(11)
SA=∑i(Yi-y)2
(12)
用F检验,即
(13)
式中:p为变量个数;n为试验次数。
本实验的变量个数p为3,试验次数n为16,依据公式(10)~(12),可以算出ST、SE、SA,再依据公式(13)求出F。3个方向的切削力计算结果如表3所示,在给定显著水平α=0.01的条件下,由于F≥F0.01(3,12)=5.95,因此进给力Fx的显著性很高,同理,背向力Fy、主切削力Fz的显著性也很高。因此,本文所建立的切削力经验公式具有一定的实用价值。
3 结语
(1)在CVD氮化钛涂层刀具高速铣削天然大理石时,切削力随着进给速度vf和切削深度ap的增加而增大,随着切削速度vc的增加而减小。
表3切削力方差分析表
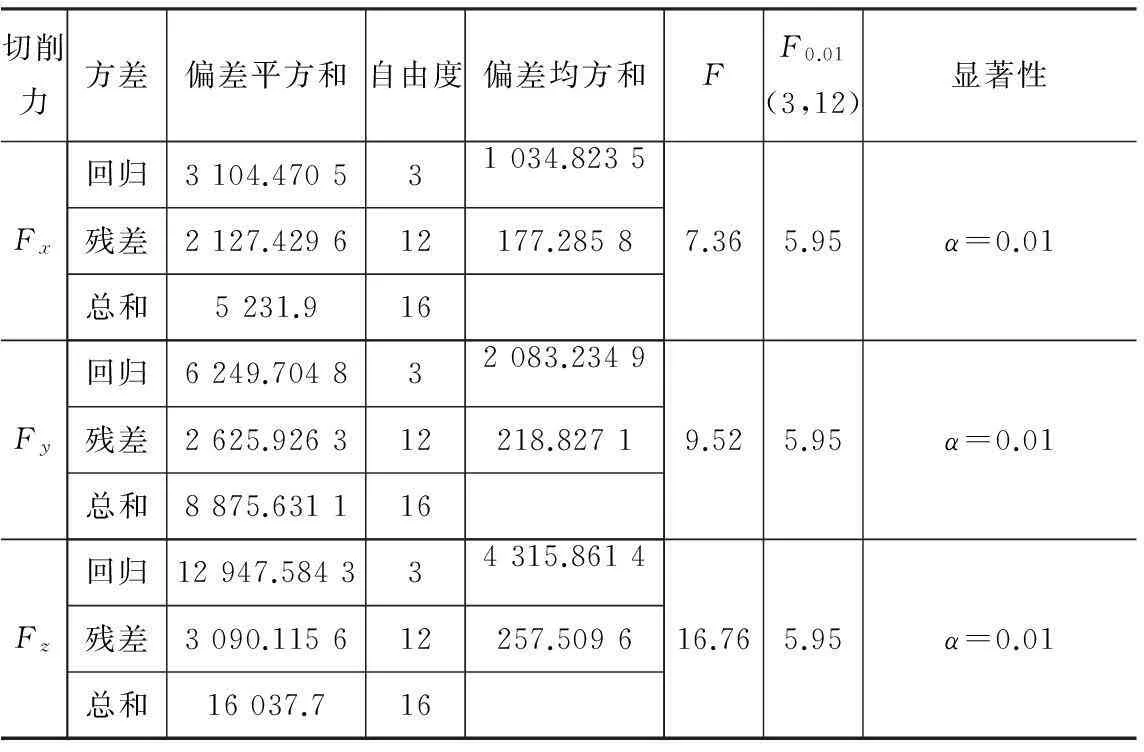
切削力方差偏差平方和自由度偏差均方和FF0.01(3,12)显著性Fx回归3104.470531034.8235残差2127.429612177.2858总和5231.9167.365.95α=0.01Fy回归6249.704832083.2349残差2625.926312218.8271总和8875.6311169.525.95α=0.01Fz回归12947.584334315.8614残差3090.115612257.5096总和16037.71616.765.95α=0.01
(2)基于试验数据的基础上,采用最小二乘法原理对预测模型的回归系数进行参数估计,对切削力预测经验公式进行相关性检验的显著性很高,表明本文建立的切削力经验公式较为准确,有一定实用价值。
(3)通过分析切削力预测经验公式可以发现:切削深度是对切削力影响最大的因素;切削速度次之;进给速度对切削力的影响最小。
[1]黎险峰. 淬硬模具钢高速切削的试验研究[D]. 大连:大连理工大学,2010.
[2]于静.高速切削淬硬模具钢切削机理的研究[D].大连:大连理工大学,2012.
[3]Hanifi Copur. Linear stone cutting tests with chisel tools for identification of cutting principles and predicting performance of chain saw machines[J]. International Journal of Rock Mechanics & Mining Sciences,2010,12(47):104-120.
[4]Julio Garrido Campos, Ricardo Marin Martin. Modelling and implementing circular sawblade stone cutting processesin STEP-NC[J]. Robotics and Computer-Integrated Manufacturing,2010,26:602-609.
[5]刘敏,景璐璐,安庆龙,等.4Cr16Mo模具钢立铣加工过程中的切削力系数[J].上海交通大学学报,2009,43(1):25-29.
[6]吴玉厚,闫广宇,赵德宏,等. CVD复合涂层刀具在天然大理石切削中的磨损特性[J]. 沈阳建筑大学学报:自然科学版,2014,30(4):712-719.
[7]王凌云,黄红辉.基于BP网络的注塑成型模具硬态高速铣削力研究[J]. 中南大学学报,2010,41(6):2218-2223.
[8]Murat Yurdakul, Hurriyet Akdas. Prediction of specific cutting energy for large diameter circular saws during natural stone cutting[J]. International Journal of Rock Mechanics & Mining Sciences,2012,53:38-44.
[9]Bagci E. 3D numerical analysis of orthogonal cutting process viamesh-free method[J]. Int.J.the Physical Sciences,2011(6):1267-1282.
[10]刘鹏,徐九华,冯素伶,等. PVD刀具高速铣削TA15钛合金切削力研究[J]. 南京航空航天大学学报,2010,42(2):224-228.
[11]陈明,安庆龙.高速切削技术基础与应用[M].上海:上海科学技术出版社,2012.
如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。
Research on cutting force of high speed milling marble using CVD coating tool
YAN Haipeng, WU Yuhou, ZONG Yupeng
(School of Mechanical Engineering, Shenyang Jianzhu University, Shenyang 110168, CHN)
The orthogonal experiments for high speed milling marble cutting force test with CVD coated toolsare designed. The effect rule of cutting force changed with single cutting parameters(cutting speed, feed speed, depth of cut)are analyzed through the experiments.The parameters cutting force coefficients of empirical formula regression are estimated using the least squares principle and the correlation of empirical formulais tested.The tested results show that significance is high. The results show that the cutting force increases with the increase of feed rate and cutting depth, and decreases with the increase of cutting speed. The depth of cut has the main influence on cutting force and followed by the cutting speed, and the feed rate is the least influence on cutting force.
CVD coating tool;marble; cutting force; cutting parameters; least squares
TG501.3;TH711
A
闫海鹏,男,1987年生,在读博士,研究方向为脆性材料加工、工艺参数优化。
(编辑汪艺)(2015-12-22)
160307
*国家自然科学基金资助项目(51375317);辽宁省自然科学基金项目(2014020069);教育部创新团队计划(ITR1160)
