SLM钛合金3D打印件铣削加工参数优化分析*

侯阳琨　袁军堂　汪振华　王博翔

(南京理工大学机械工程学院，江苏 南京 210094)



SLM钛合金3D打印件铣削加工参数优化分析*

侯阳琨袁军堂汪振华王博翔

(南京理工大学机械工程学院，江苏 南京 210094)

针对SLM钛合金3D打印件表面质量无法满足装配精度要求，仍需进行二次加工的需求，设计正交试验方案，建立表面粗糙度的预测模型并进行铣削参数优化分析，为SLM钛合金3D打印件铣削加工的切削参数选择提供依据。首先，对实验数据进行多元线性回归，建立适用于SLM钛合金件的铣削加工表面粗糙度数学预测模型，给出了切削速度、每齿进给量、轴向切深及径向切深与表面粗糙度的量化关系；建立以加工效率和表面粗糙度为优化目标的多目标切削参数优化模型，使用Pareto最优解集理论进行多目标切削参数优化，优化结果表明在切削速度130 m/min，每齿进给量0.01 mm/齿，轴向切深0.40 mm时可以得到较好的加工表面粗糙度及较高的加工效率。

SLM；钛合金；表面粗糙度；参数优化

钛合金具有密度小(约4.5 g/cm3，仅为钢的60%)，比强度高，热强度高，能耐各种酸、碱、海水、大气等介质的腐蚀等一系列优良的力学、物理性质，因此在航空航天业、炼油业、核废料储存、电化学、医疗设备等领域得到越来越广泛的应用[1]。随着钛合金3D打印技术上的突破，3D打印钛合金部件已经开始用于新型战机和大型民航机上。采用3D打印技术进行生产加工既可以节省材料成本，又能缩短加工时间，具有广阔的发展前景。3D打印钛合金件的力学性能已经可以接近锻造水平，但是表面工艺仍不精细，表面粗糙度一般只有15～50 μm左右，无法满足装配精度要求，需要在3D打印的基础上进行二次切削加工。

国内外学者对于一般的热轧及锻造钛合金工件的切削加工进行了大量的研究，取得了一定的成果。陈建岭[2]通过对TC4钛合金板材进行高速铣削试验，对TC4钛合金高速铣削的切屑形态、切削力、切削温度、表面完整性进行了研究，并进行了铣削参数优化。范依航[3]对TC4棒料进行了车削试验，研究了切削力、切削热、刀具材料及切削参数对刀具磨损的影响规律，并以提高刀具寿命为目标进行了车削参数优化。

目前，对于3D打印钛合金的研究还主要集中在材料力学性能和成型工艺参数方面。陈静[4]等对3D打印TC4钛合金试件进行了拉伸试验，研究发现和锻造件相比3D打印钛合金试件具有高强低塑的特点和更加明显的各相异性。张升[5]等利用扫描电子显微镜及X 射线能谱分析等检测方法，对TC4 钛合金在3D打印过程中裂纹的开裂行为及其形成机理，发现通过控制成形的工艺参数来控制晶粒大小和生长方向，可以达到调控制件微观组织的目的，改善制件的性能，减少并抑制裂纹的产生。

但是，对于3D打印钛合金材料的切削加工工艺性能的研究，目前还较少，没有系统的研究成果，切削参数的选择还沿用切削普通钛合金的标准，无法保证切削效率和加工质量，建立切削此类材料的工艺规范是一个亟待解决的问题。

选择性激光熔化(SLM)是金属件直接成型的一种方法，是3D打印技术的最新发展[6]。本文以SLM钛合金3D打印件为研究对象，进行铣削加工实验，并建立表面粗糙度预测数学模型，进而进行铣削加工切削参数优化，为钛合金3D打印件在实际加工中的切削参数选择提供依据，并达到提高生产效率及表面加工质量的目标。

1　实验条件及方案设计

实验采用刀具直径为3 mm的TiAlN涂层硬质合金两刃平底铣刀，螺旋角为45°，螺旋方向为右旋。表面粗糙度测量采用Dektak XT探针式台阶仪测量3次取算术平均值。SLM钛合金选用Ti-6Al-4V粉末，在Concept Laser M2金属3D打印机上打印成形。实验在瑞士WILLEMIN公司生产的408S2五轴加工中心上进行。

铣削加工时，以切削速度vc、每齿进给量fz、轴向切深ap和径向切深ae为变量，研究切削参数对加工表面粗糙度的影响，采用L16(45)安排正交试验，参考切削手册中铣削一般钛合金时的参数选择，设计实验参数如表1所示。

表1　正交试验参数表

2　试验结果与预测模型建立

2.1正交试验结果

根据L16(45)正交表对SLM钛合金件进行铣削实验并进行表面粗糙度测量，图1为铣削加工现场。

由正交试验测得的表面粗糙度Ra如表2所示。

表2　表面粗糙度正交试验结果

2.2表面粗糙度预测模型建立

在加工设备、刀具和工件材料等条件确定的情况下，根据金属切削原理可知表面粗糙度和切削参数之间存在指数关系，常用的基于正交试验方法获得铣削工件表面粗糙度数学预测模型可以表示为：

(1)

式中：C为由材料和加工条件所决定的系数；vc为切削速度,mm/min；fz为每齿进给量,mm/齿；ap为轴向切深，mm；ae为径向切深，mm。b1，b2，b3，b4为切削参数对表面粗糙度的影响系数。

为确定模型中各系数，首先对方程两边取对数，将非线性方程转化为线性方程。

ln

Ra=lnC+b1lnvc+b2lnfz+b3lnap+b4lnae

(2)

其中令y=lnRa，b0=lnC，x1=lnvc，x2=lnfz，x3=lnap，x4=lnae，方程简化为：

y=b0+b1x1+b2x2+b3x3+b4x4

(3)

式(3)即为转化后的以x1，x2，x3，x4为变量的多元线性方程。

根据正交试验，考虑实验过程中存在随机误差ε，则多元线性回归方程可表示为：

式中：xi1，xi2，xi3，xi4表示第i组实验的4个自变量，对应的因变量为yi，其中i=1，2，3……16。εi为随机误差，且满足E(ε)=0。

若记

则式(4)可写成

Y=Xβ+ε

(5)

采用最小二乘法估计参数β，设b1、b2、b3、b4分别为β0、β1、β2、β3、β4的最小二乘估计，则

(6)

式中:X′为X的转置矩阵，(X′X)-1为X′X的转置矩阵。

将正交试验数据取对数，带入矩阵X和Y中，求得表面粗糙度多元线性回归系数的最小二乘估计为：

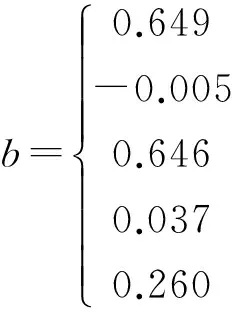
(7)

则SLM钛合金3D打印件的铣削加工表面粗糙度数学预测模型为：

Ra= 1.91·vc -0.005·fz0.646·ap0.037·ae0.26

(8)

选取α=0.005对回归方程进行F值显著性检验，F=47.185>F0.005(4,11)=6.88。F检验结果落在拒绝域内，拒绝原假设，认为线性回归效果显著，表面粗糙度预测模型与实验数据拟合程度很高。

2.3预测模型的准确性检验

预测模型回归效果显著，还需进一步进行预测准确性检验，检验模型的预测精度。随机选取5组不同于正交试验的切削参数组合，进行铣削加工实验，并将切削参数带入预测模型与实验结果进行对比。预测值与实验实测值对比结果如表3所示。

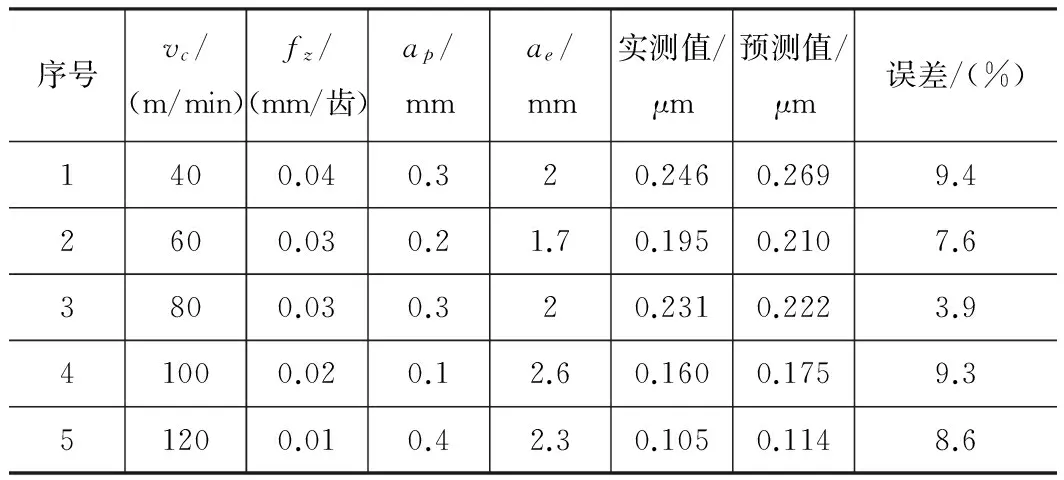
表3　表面粗糙度预测值与实验实测值对比

由表3可知，应用数学预测模型进行表面粗糙度预测，预测结果与试验结果误差控制在10%以内，可以较为准确地对SLM钛合金3D打印件铣削加工表面粗糙度进行初步的预测。

3　铣削参数优化分析

3.1Pareto优化解集的理论基础

多目标优化问题指在可行域内确定变量取值，从而使各目标函数尽量同时达到最小。其数学表达可以描述为：

(9)

式中：gi(X)为约束条件；Ω为变量X的可行域。

在多目标优化问题中，各个目标一般是相互制约的，一个目标的优化会导致其他目标性能的降低，通常不存在使各个目标同时达到最小的绝对最优解。这些在改进任何目标函数的同时,必然会削弱至少一个其他目标函数的解被称为非支配解或Pareto最优解，这些解的集合构成了多目标优化的解，即著名的Pareto最优解集[7]。

在向量可行域范围内，如果不存在向量X*，使得对于任意i，都有fi(X*)≤fi(X)，则X被认为是此多目标优化的一个Pareto最优解，由所有Pareto最优解所构成的解空间在空间上形成的曲面称为Pareto前沿面，如图2所示。

3.2铣削参数多目标优化

为了在SLM钛合金材料的铣削加工过程中获得较高的加工效率和较好的加工表面质量，选取单位时间材料去除率和表面粗糙度为目标函数，在变量可行域范围内，建立多目标优化模型。由于优化算法通常是实现最小值优化，所以将单位时间材料去除率转化成以单位体积材料加工时间(min/mm3)为目标函数，建立优化模型如式(10)所示。

X=[x1,x2,x3,x4]T

(10)

式中：自变量x1、x2、x3、x4为铣削参数，约束条件为经验模型参数取值范围，目标函数f1(X)和f2(X)分别代表表面粗糙度和单位体积材料加工时间。

采用NSGA-Ⅱ非劣排序遗传算法进行多目标切削参数优化，得到Pareto前沿面，如图3所示。

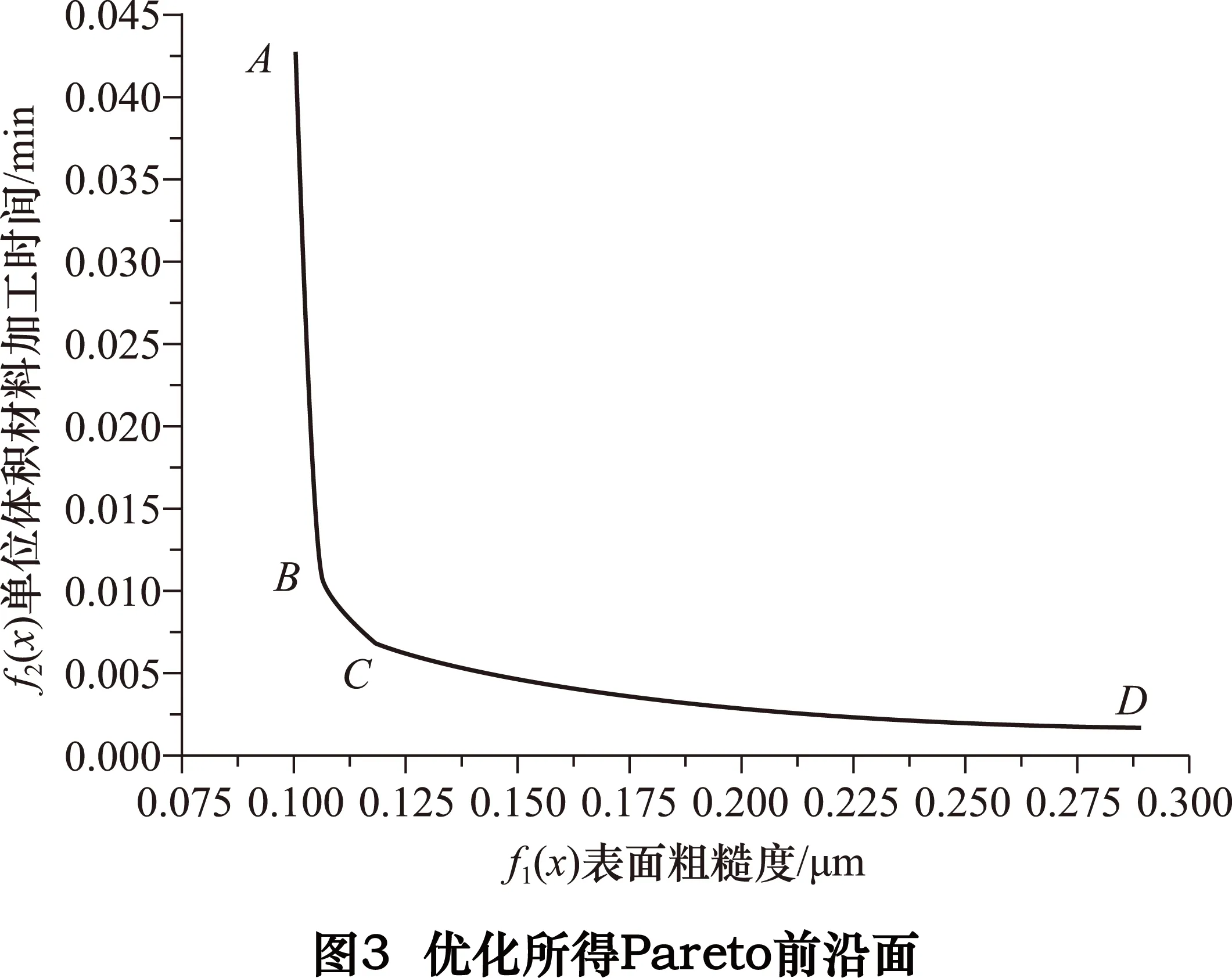
根据图3中的Pareto前沿面变化趋势，可以看出：在AB区间段，随着表面粗糙度值的减小，单位体积材料加工时间急剧增加，说明在此区间中，不适于再减小表面粗糙度值，减小少量的表面粗糙度值会导致增加大量的加工时间成本，加工效率成倍降低；在CD区间段，随着表面粗糙度值的减小，单位体积材料加工时间缓慢增加，趋势较为平稳，说明在此区间中降低少量的切削效率，可以较大程度的提升表面加工质量，可以在加工时间允许的情况下，适当的降低加工效率，减小表面粗糙度值；在BC区间段，随着表面粗糙度值的减小，单位体积材料加工时间出现了明显的拐点，即此区间为两个目标函数的制衡区间，任何一个目标函数的少量减小，都会导致另一个目标函数值的剧增。

综上所述，BC区间段的结果较为理想，既提高了表面加工质量，又保证了一定加工效率，是Pareto前沿面的期望解集，BC区间的Pareto点的数据信息如表4所示。

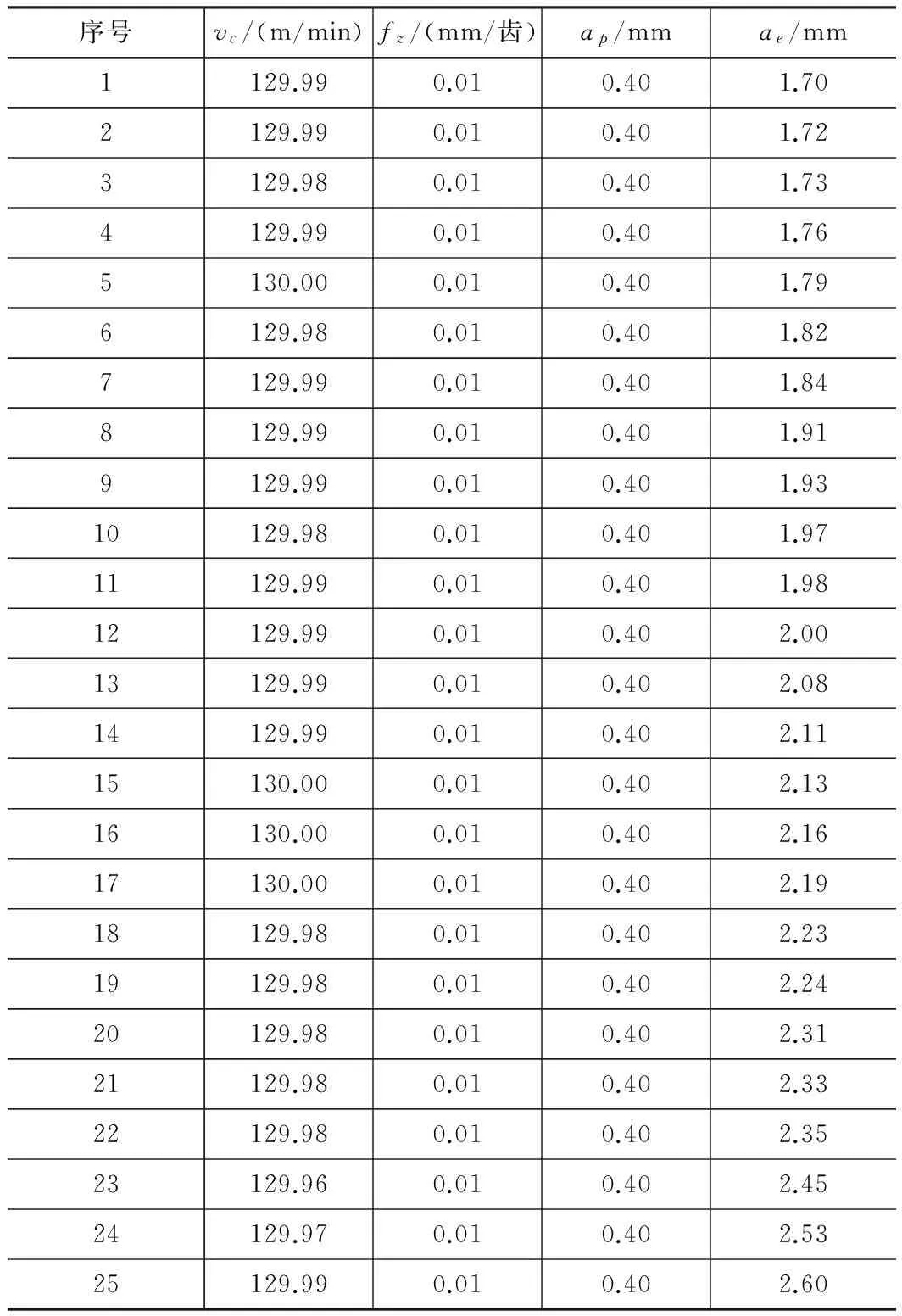
表4　Pareto解集BC区间数据信息

最终确定优化后的铣削参数为：铣削速度130 m/min，每齿进给量0.01 mm/齿，轴向切深0.40 mm，径向切深可以根据加工要求选取合适的取值。取较大的径向切深使结果趋向C点，即提升切削效率，降低一定的加工质量；取较小的径向切深使结果趋向于B点，即牺牲一定的切削效率来提升表面加工质量。

4　结语

(1)利用多元线性回归，建立了适用于SLM钛合金3D打印件的表面粗糙度经验模型，根据F检验，发现回归程度高度显著。利用经验模型对表面粗糙度进行预测，与实验数据进行对比，预测与实验误差和在10%以内，预测结果准确可靠。

(2)以表面粗糙度和单位体积材料加工时间为目标函数，对铣削参数进行多目标优化分析。发现在切削速度130 m/min，每齿进给量0.01 mm/r，轴向切深0.40 mm时，切削SLM钛合金3D打印件可以在保证一定的加工效率的同时得到较好的表面粗糙度。

[1]林翠，杜楠.钛合金选用与设计[M].北京：化学工业出版社，2014.

[2]陈建岭.钛合金高速铣削加工机理及铣削参数优化研究[D].济南：山东大学，2009.

[3]范依航.高效切削钛合金Ti-6Al-4V刀具磨损特性及切削性能研究[D].哈尔滨：哈尔滨理工大学，2011.

[4]陈静，张霜银，薛蕾，等.激光快速成型Ti-6Al-4V合金力学性能[J].稀有金属材料与工程，2007，36(3)：475-479.

[5]张升，桂睿智，魏青松，等. 选择性激光熔化成形TC4 钛合金开裂行为及其机理研究[J].机械工程学报，2013，49(23)：21-27.

[6]Yadroitsev I,Shishkovsky I, Bertrand P，et al. Manufacturing of fine-structured 3D porous filter elements by selective laser melting [J]. Applied Surface Science, 2009, 255(10): 5523-5527.

[7]郑金华.多目标进化算法及其应用[M]，北京：科学出版社，2007.

(编辑李静)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Milling parameters optimization and analysis of selective laser melted Ti-6Al-4V

HOU Yangkun, YUAN Juntang, WANG Zhenhua, WANG Boxiang

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, CHN)

To meet the requirement that the selective laser melted Ti-6Al-4V needs milling process to improve its surface quality, a mathematical model of surface roughness is founded based on orthogonal experiment to optimize the milling parameters, which gives a basis to choose appropriate milling parameters of selective laser melted Ti-6Al-4V. Firstly, the prediction model of surface roughness is established based on experimental data to give the relationship between milling parameters and surface roughness; then an optimization model is founded and the milling parameters is optimized by Pareto theory, the conclusion shows that the high processing efficiency and smooth surface can be guaranteed by using cutting speed 130 m/min, feed engagement 0.01 mm/r and cutting depth 0.40 mm.

selective laser melted; Ti-6Al-4V; surface roughness; parameters optimization

TH161+.14

A

侯阳琨，男，1991年生，硕士研究生，主要研究方向为钛合金高速铣削加工。

2015-07-14)

160127

*国家自然科学基金(51275247)