基于特征加权的朴素贝叶斯主轴热误差建模*

邓勇军　张之敬　金　鑫　张朝枭　孙宏昌

(北京理工大学，北京 100081)



基于特征加权的朴素贝叶斯主轴热误差建模*

邓勇军张之敬金鑫张朝枭孙宏昌

(北京理工大学，北京 100081)

采用基于特征加权的朴素贝叶斯方法，对铣削电主轴热误差进行了建模及预测研究。根据不同特征对热变形影响程度的不同，采用信息增益的方法计算了不同特征的权重，基于实验得到的数据，建立了轴径向热变形误差模型，从预测结果看，模型具有比较好的预测功能。

特征加权；朴素贝叶斯；信息增益；热误差建模

微小型车铣复合加工机床中，铣削电主轴由于高速旋转，产生大量热量，由此而引起主轴热变形，造成工件和铣刀之间的相对位置变化，影响加工精度。主轴热误差成为微小型工件加工中不可忽视的主要误差源之一[1]。

近年来，随着国内外学者对高精度机床热误差的重视，多种误差建模方法被采用，传统方法如最小二乘法，智能建模方法如神经网络、支持向量机和贝叶斯网络法成为热误差建模和误差预测的有效手段。然而这些方法主要是针对常规机床和重型机床，对于精密微小型车铣复合加工机床鲜有涉及，而且这些方法对于热特征的重要程度在建模中体现不足，无法很好的反映实际情况。

本研究以北京理工大学自主开发的第三代精密微小型车铣复合加工机床CXKM25-Ⅲ所使用的小型铣削电主轴为研究对象，通过热误差检测实验获得空转条件下的主轴温度变化和热变形数据，采用基于特征加权的朴素贝叶斯方法对主轴热误差进行建模和预测，为后续热误差补偿研究提供依据。

1　主轴热误差检测实验

1.1实验方法和测点设置

由于高速旋转，电主轴的主要热源在其轴承处和电动机部位，采用精度为0.1 ℃的温度传感器配合温度巡检仪，将温度测点分布在电主轴前端轴承、中部定转子和后端轴承和电动机处。另外机床与环境之间还存在热交换，将环境温度传感器裸露在空气中即可。在主轴上布置6个温度传感器，环境中设置1个温度传感器。由于主轴高速旋转中，锥孔温度不易测量，故使用红外热像仪进行测量，具体测点设置如表1所示。

表1　温度测点设置

由于主轴前端的轴、径向热变形影响加工精度，采用高精度电感测微仪进行测量，两个测头分别固定在主轴前端面和径向方向，测点设置如表2所示。

表2　位移测点设置

转速是影响主轴热变形的主要工况参数，本实验主要对空载状态下，不同转速时电主轴的机体进行温升和变形测试，从机床冷态开始测量，给主轴50%的工作转速让其转动并逐步升到工作转速，分别在不同转速n=4 000 r/min、7 500 r/min、12 000 r/min下空转120 min，测量主轴各测点温度变化和热变形。采集软件采样间隔最小为5 s，可以连续记录数据。

1.2实验和数据分析

实验现场测试如图1所示。

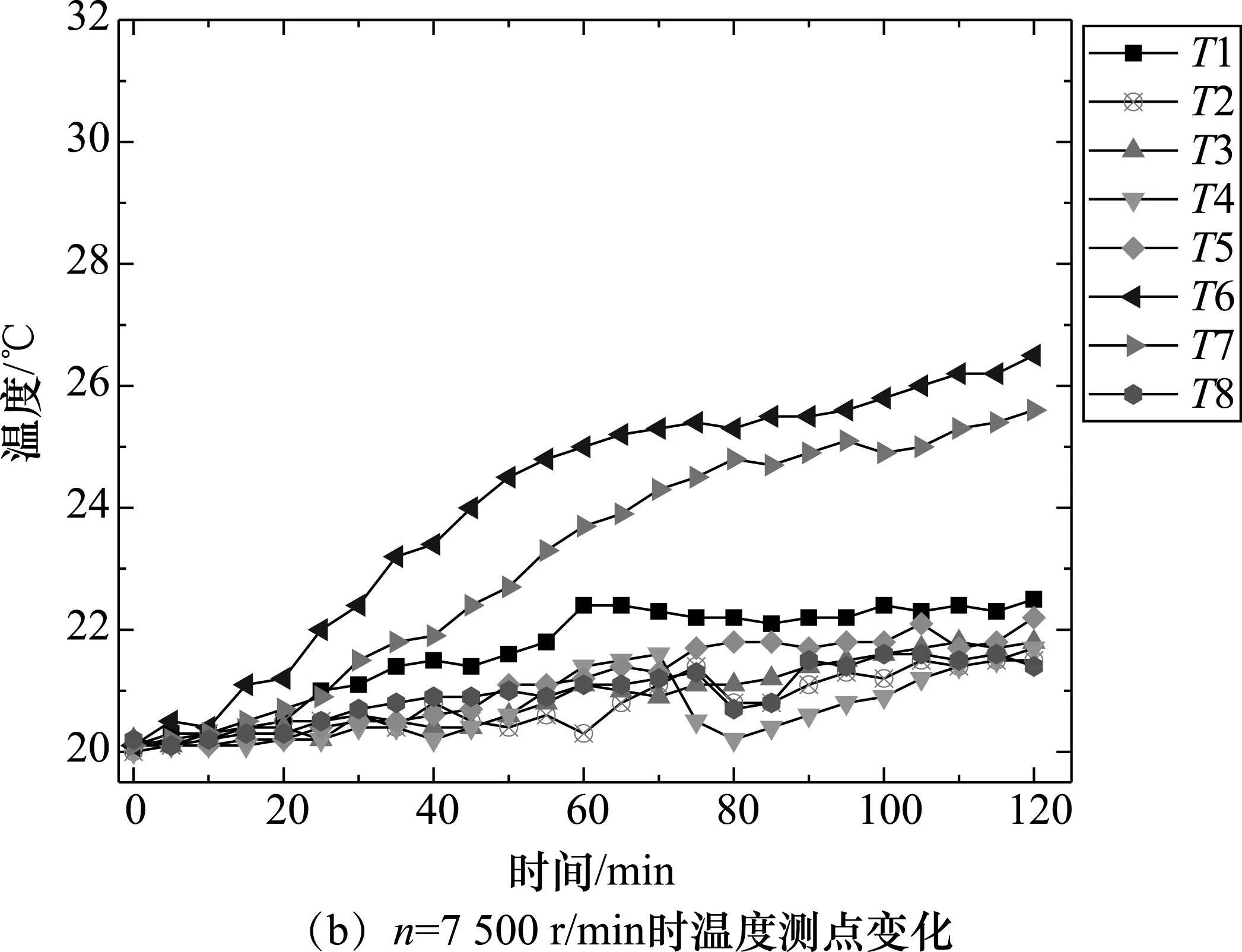
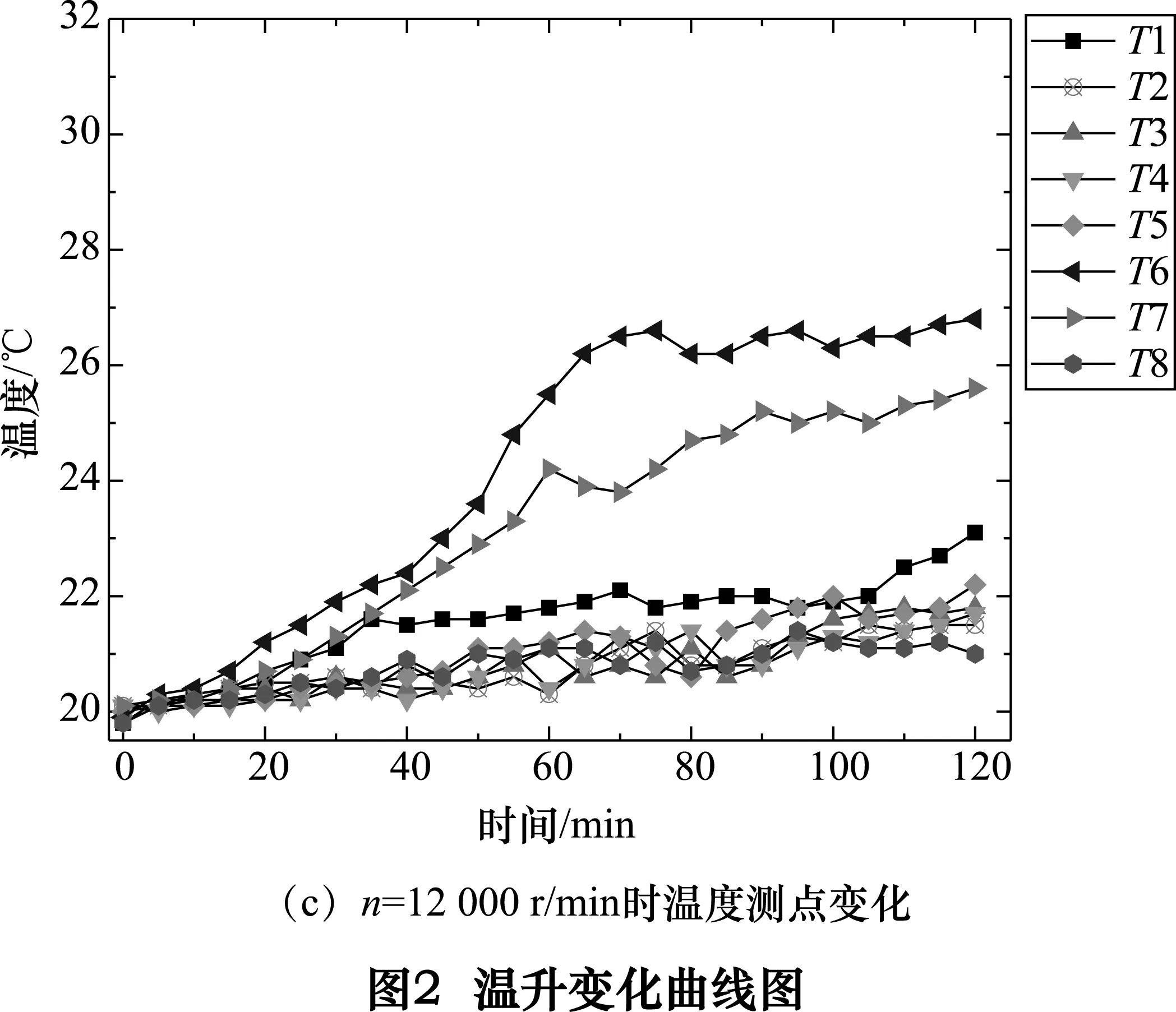
实验的温度数据和热变形数据是在同样频率下测量的，以5 min为记录点，将不同转速下各个测点温升和热变形绘制成曲线，分别如图2和图3所示。

由图2可知，测点处的温度随着铣削电主轴转速的增加而呈上升趋势。其中主轴电动机处(T6)处温度最高，这是因为高速旋转过程中，主轴后端电动机发热造成的。锥孔处(T7)次之，主轴锥孔处于轴心位置，轴承发热及电动机发热都会向此处传递，且离冷却管道较远，散热条件较差，因此该测点温度也较高。主轴中部固定在抱夹单元中，测点T3、T4测试时只是测量了抱夹单元外壳位置，因此温升较低。主轴系统自身带有测温传感器，为保证运行过程中精度，通过调节冷却油的流量来保持主轴工作在较低温度。所以T1、T2和T5处温升较低。当主轴转速达到12 000 r/min时，最大温差达到6.9 ℃，最小为环境温升为1.2 ℃。当工作1 h左右，温升保持平衡并缓慢增长，说明主轴已处于热平衡稳定状态。

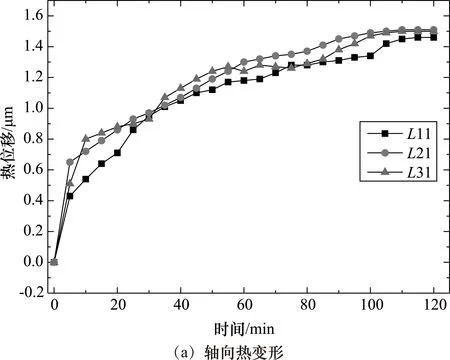
主轴热变形曲线如图3所示，L11和L12、L21和L22、L31和L32分别表示转速为4 000 r/min、7 500 r/min和12 000 r/min时主轴轴向和径向热变形。

从图3可以看出，在主轴启动后短时间内，主轴轴、径向热变形较快，这是因为主轴是逐步由低速启动而达到工作速度的，初始变形中，主要因素是主轴转动过程中自身振动造成的。在达到热平衡状态时，温升曲线和热变形曲线走势一致。对比两图可以看出，主轴Z方向和X方向热变形曲线趋势基本一致。但是，比较而言，X方向的热变形，数值要大，而Z方向的热变形数值小，是因为实验中热变形数值里包含了主轴跳动值，根据主轴出厂检验报告，主轴径向跳动大于轴向跳动，所以导致实验中的径向热变形略大于轴向热变形。

2　基于特征加权的朴素贝叶斯误差建模与预测

2.1基于特征加权的朴素贝叶斯方法

采用朴素贝叶斯模型进行分类时，假定每个属性特征之间是相互独立的，并且每个特征对分类的贡献度都是一样的。然而，在真实的环境中，这些假设条件都难以满足，结果导致分类准确率降低。特征加权是一种可以保留或删除特征的方法，特征越重要，赋予的权值越大，而不太重要的特征赋予较小的权值。

特征加权的朴素贝叶斯分类器概率计算公式为

(1)

其中：ωk∈R+，代表特征的重要程度，即为权重；P(B)代表先验概率,P(Ak|B)为类条件概率，表示在B出现时，取AK的概率。

在基于特征加权的朴素贝叶斯热误差模型中，Ti(i=1,2,…，n)表示测量的温度，Erj(j=1,2,…，m)表示主轴的热变形误差。记P(Erj|Ti)表示Ti温度的条件下出现Erj误差的联合条件概率分布，根据贝叶斯定理可得：

(2)

特征加权的朴素贝叶斯模型认为不同位置的测量温度对热变形误差的影响不同，根据式(1)、(2)，得到：

(3)

2.2特征权重计算

本文采用信息增益方法计算温度变量的权重，如式(4):

IG(Ti)=H(Er)-H(Er/Ti)

(4)

其中：IG(Ti)表示特征Ti的信息增益值；Er表示误差区间；H(Er)表示在没有考虑特征Ti时，预测误差取值属于某个区间概率空间的熵，即对预测结果的不确定程度；H(Er/Ti)为考虑特征Ti后，误差取值属于某个区间概率空间的熵，即特征Ti对预测结果的不确定程度。

温度变量权重值计算的基本原理如下：计算没有考虑特征Ti时的信息熵与考虑Ti时的条件熵之间的差值，即信息增益来确定特征所携带的信息量，信息增益值越大则该特征携带的分类信息越多，在分类过程中越重要，应该赋予较高的权重；反之则该特征携带的信息量较小，应该赋予较低权重。同时采用Han等人[2]提出的min-max方法对温度变量权重进行标准化操作。

2.3误差模型建立

首先，根据训练集构造模型；然后，采用新实验数据对模型进行更新优化，随着数据的累积，使所建立的模型更加符合主轴自身的热特性；最后，根据所建模型以及机床加工过程中采集到的实时温度数据预测该时刻下主轴相应的热变形量。构建的热误差模型结构如图4所示，热误差模型将实验中的温度测点和转速选取为误差特征，预测参数为主轴热变形。

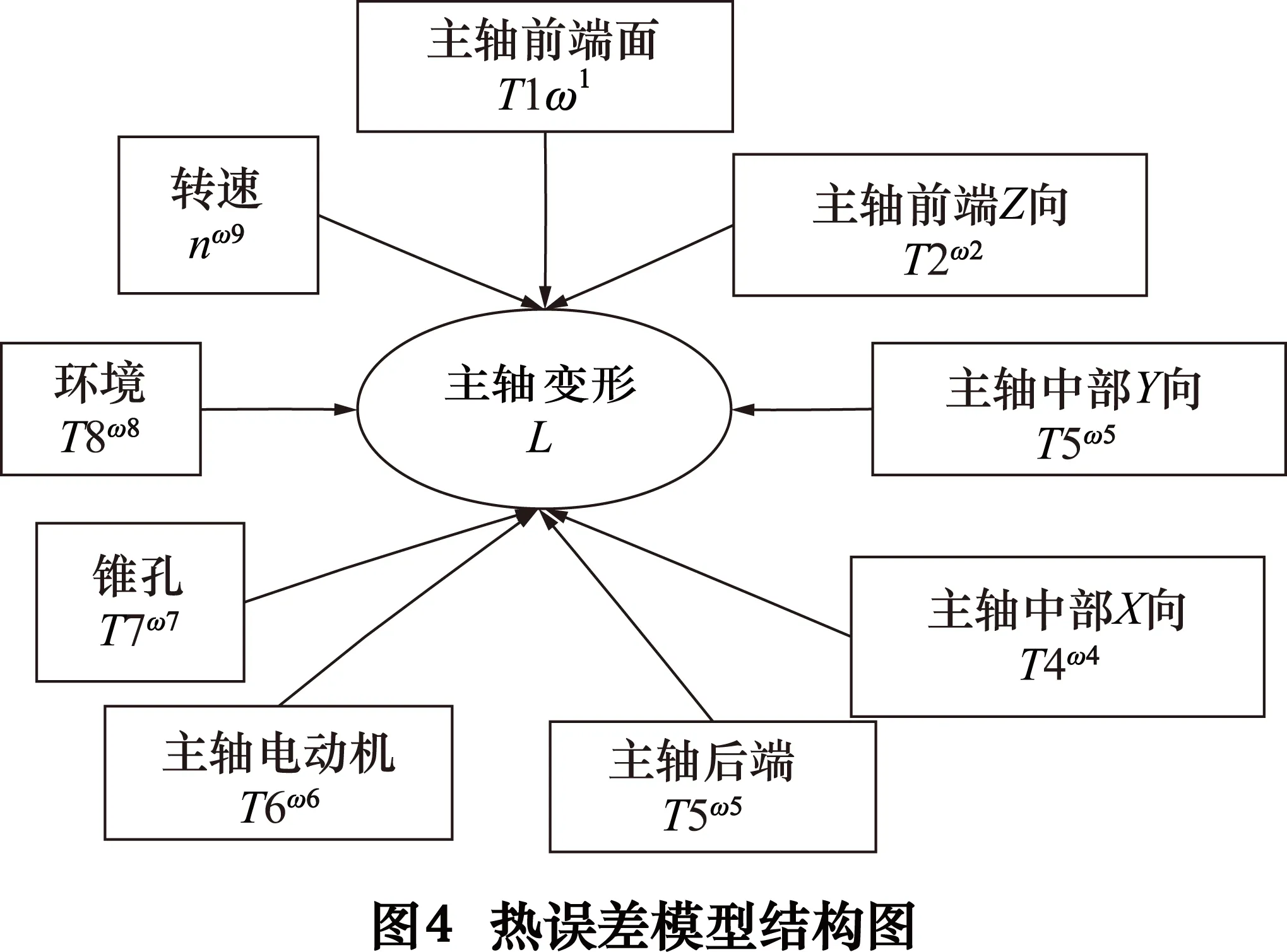
(1)数据集

数据根据空载转速分3种情况：n=4 000r/min、7 500r/min、12 000r/min，每种情况下都有一组10个结点数据。

(2)数据预处理

采集的热误差记录中的温度及热变形数据都属于连续取值，需将这些值进行离散化处理，才能用于热误差模型的构建及预测。本文采用等宽离散化方法将温度及热变形数据进行离散化后，再估计其条件概率。温度及热变形数据统计特征如表3所示。

表3　空载条件下特征统计

基于表3中各变量的统计特征值，对各变量进行离散化，空载条件下，除转速外，其他变量共划分为7个区间，如表4所示。

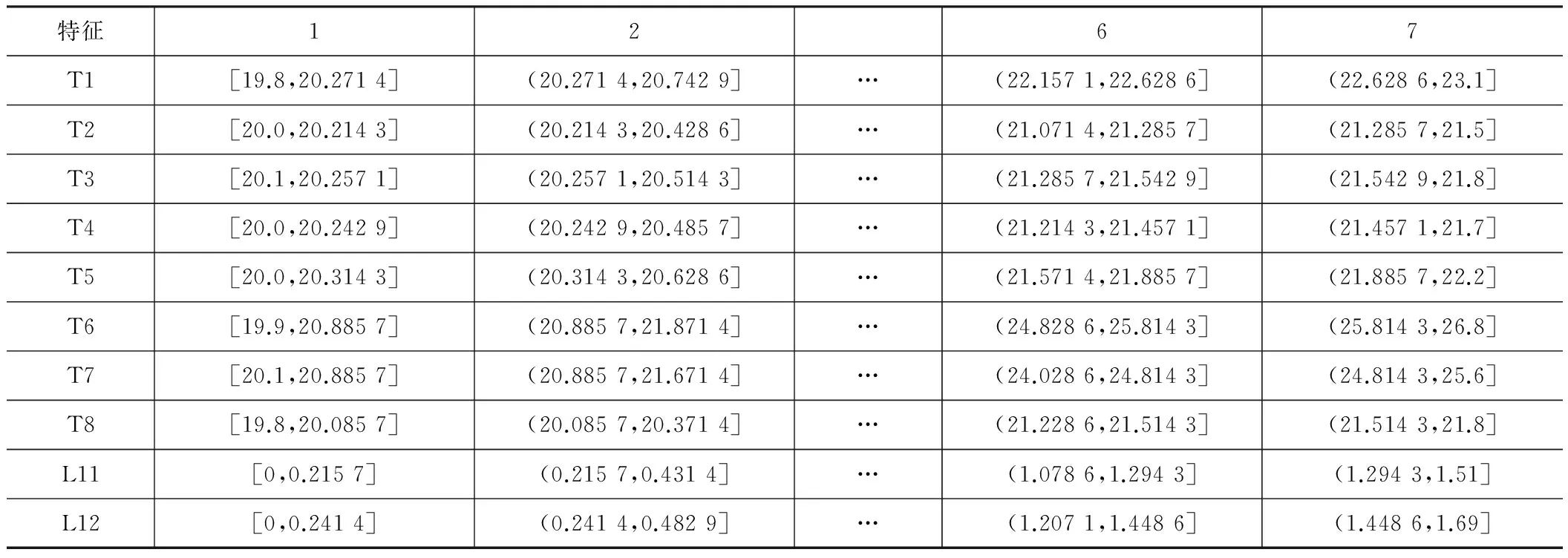
表4　空载条件下各变量离散化

考虑到误差特征对误差的影响程度不同，越重要的特征赋予的权值越大，不太重要的特征赋予较小的权值。首先通过信息增益的方法对误差特征计算权值，空载条件下轴、径向误差特征权重值分别如表5和表6所示。

表5　空载条件下轴向误差特征权重值

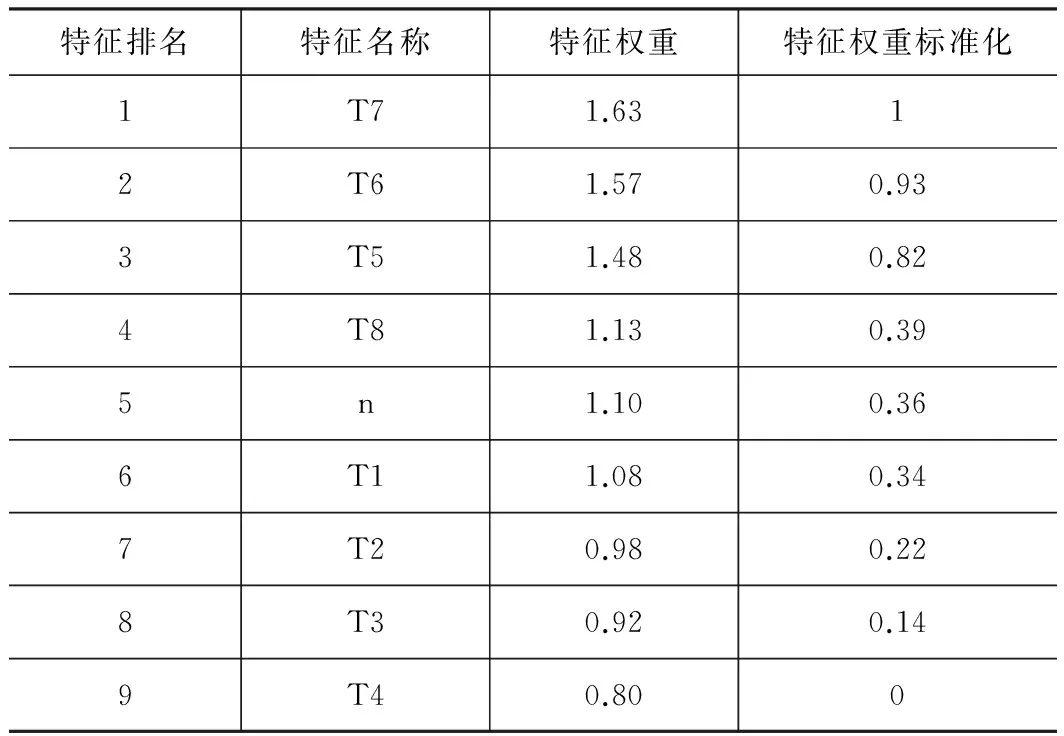
表6　空载条件下径向误差特征权重值

2.4热误差预测

采用空载条件下的数据集对轴向和径向误差预测模型进行训练，训练集为DataSet1和DataSet2，然后再分别使用另外两组测试集数据对模型进行测试，分别为Test1和Test2，每组实验重复10次，取10组实验的平均值作为实验结果。得到空载条件时，轴向误差预测准确率为88%，预测结果如表7所示，径向误差预测准确率85%，预测结果如表8所示。

根据表7、表8的数据绘制热误差曲线，如图5、图6所示。

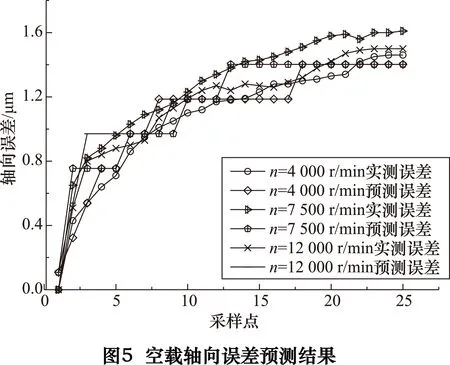
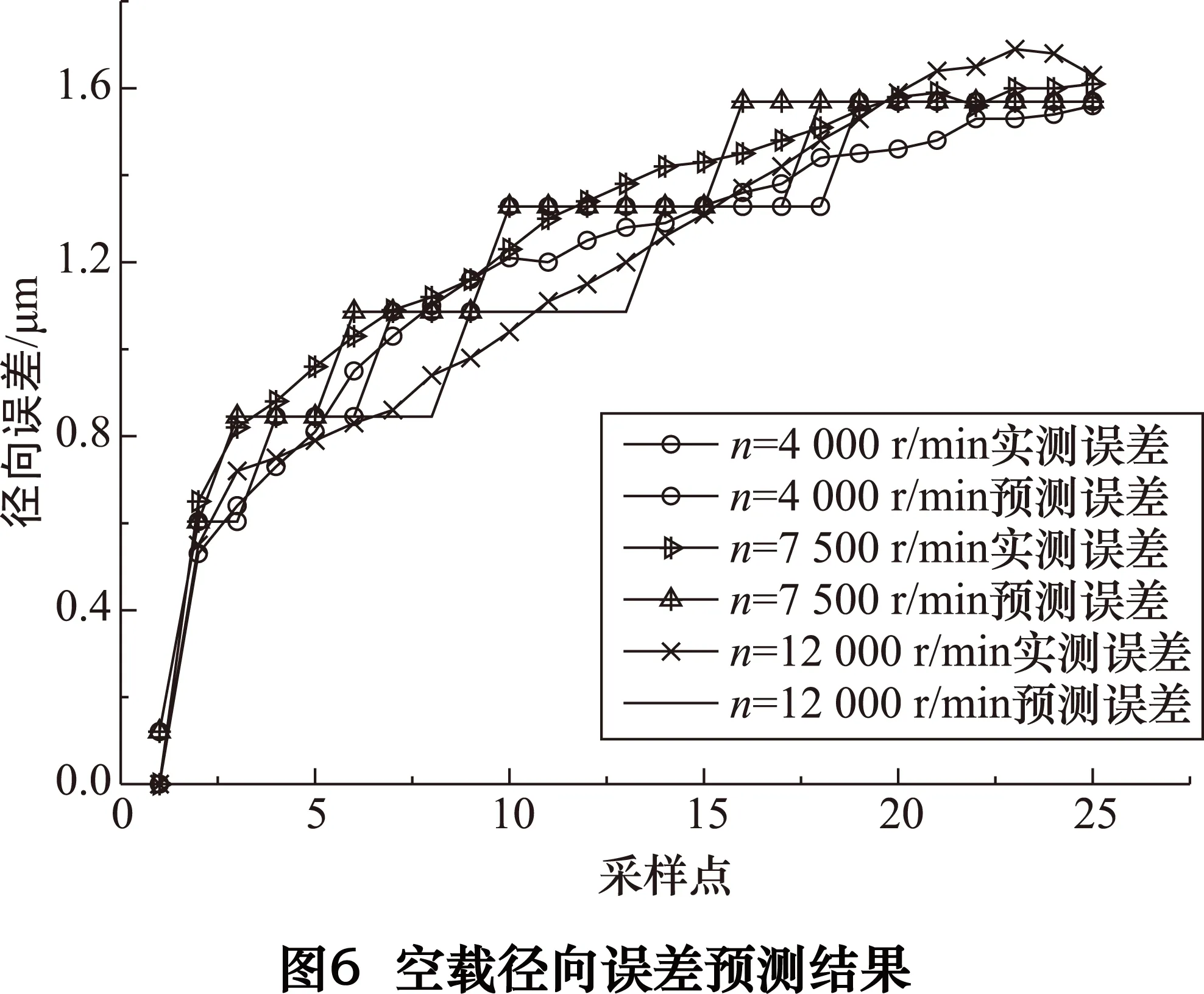
表7　空载条件下轴向误差预测结果

从图5和图6可以看出，在空载条件下，不同转速时误差预测的结果与实测值较为接近，轴向预测误差带宽最大不超过0.2μm，径向预测误差带宽最大不超过0.15μm。同时，通过预测值和实测值对比也可以看出，随着采样点的增加，基于特征加权的朴素贝叶方法的预测精度越来越高。

3　结语

通过本文对微小型车铣复合加工机床铣削电主轴热误差建模的研究得到如下结论：

(1)由于对误差特征采用了信息增益的方法进行了权值计算，表明了各特征对热变形误差的影响权重，使得最终误差预测比较精确，验证了基于特征加权的朴素贝叶斯主轴热误差模型的正确性。

(2)把基于特征加权的朴素贝叶斯方法用于主轴热误差建模，扩展了该方法的应用范围，为解决数控机床的热误差建模提供了一个有效的思路。

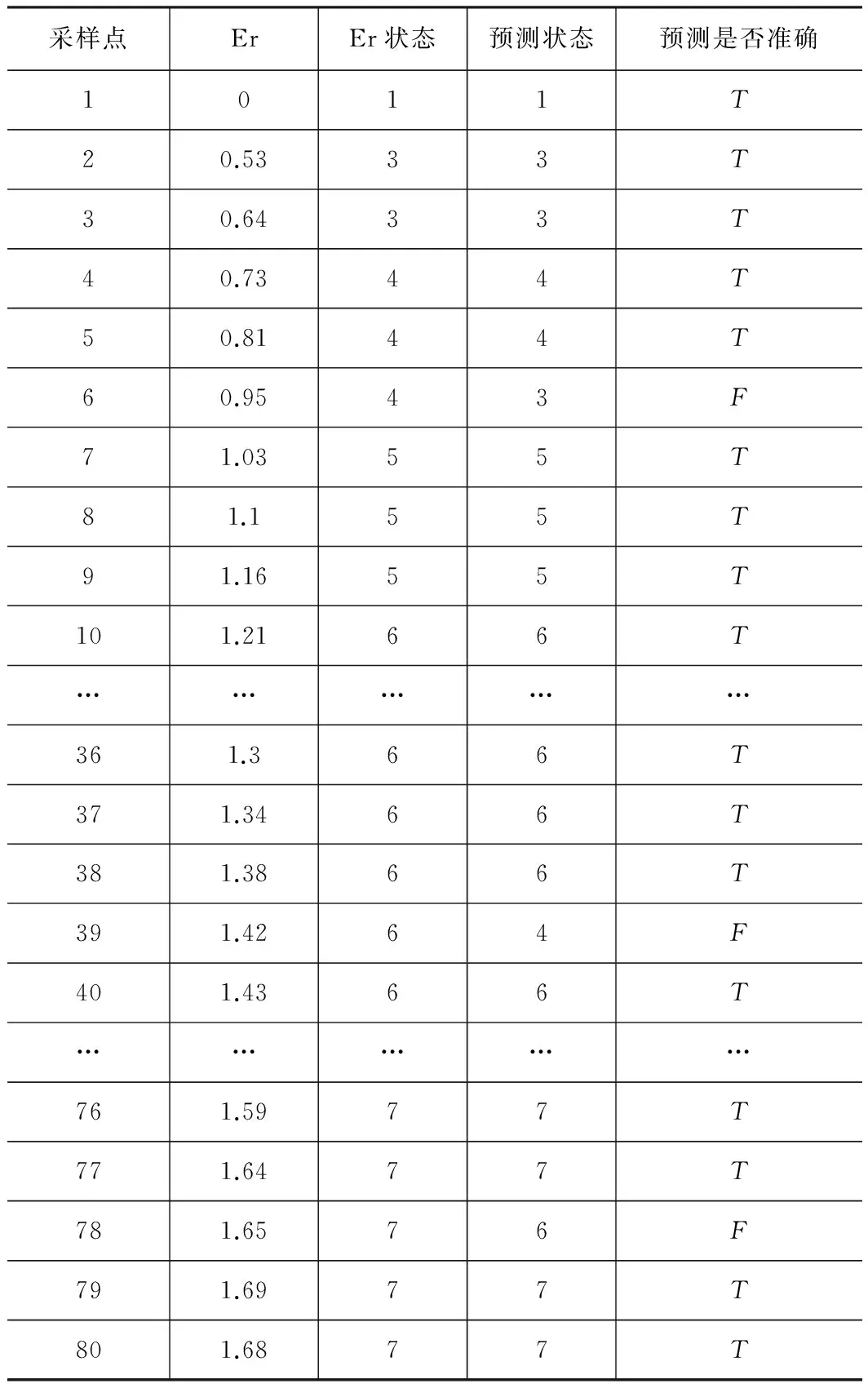
表8　空载条件下径向误差预测结果

[1]张之敬，金鑫. 精密微小型车铣复合加工技术[M]．北京：国防工业出版社, 2014．

[2]HanJ,KamberM.Datamining:conceptsandtechniques[M].SanFrancisco:MorganKaufmann, 2001.

[3]GB/T17421.3-2009,机床检验通则第3部分：热效应的确定[S]. 北京: 中国标准出版社, 2009.

[4]李海瑞.基于信息增益和信息熵的特征词权重计算研究[D].重庆: 重庆大学, 2012.

[5]白福友.基于贝叶斯网络的数控机床热误差建模研究[D].杭州:浙江大学, 2008.

[6]吴雄彪,姚鑫骅,傅建中. 基于贝叶斯网络的数控机床热误差建模[J]. 中国机械工程, 2009, 10(3): 293-296.

(编辑李静)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Thermal error modeling of spindle based on feature weighted Naive Bayes

DENG Yongjun, ZHANG Zhijing, JIN Xin, ZHANG Chaoxiao, SUN Hongchang

(Beijing Institute of Technology, Beijing 100081, CHN)

Method of feature weighted Naïve Bayes is used for modeling and forecasting thermal error of electrical spindle. According to the influence on thermal deformation, different weights of characteristics are calculated using information gain method. The error model of the thermal deformation is established based on the experimental data. The prediction results show that the model has a good prediction function.

feature weighted; Naïve Bayes; information gain; thermal error modeling

TG659

A

邓勇军，男，1983年生，博士研究生，研究方向为精密微小型车铣复合加工技术。

2015-04-14)

160113

*国家科技重大专项(2012ZX04010-061);国防基础科研项目(A2220132002)