基于μ分析的高超声速飞行器再入轨迹评估
2016-08-30李伟杰沈作军
李伟杰, 沈作军
(北京航空航天大学 航空科学与工程学院, 北京 100191)
基于μ分析的高超声速飞行器再入轨迹评估
李伟杰, 沈作军
(北京航空航天大学 航空科学与工程学院, 北京 100191)
为解决高超声速飞行器再入过程中存在的不确定性问题,将μ分析理论应用到标称再入轨迹的评估中。采用线性稳定储备准则,在密度、升力系数和阻力系数存在不确定性时,对标称轨迹在制导律下的制导稳定性进行了分析;根据所获得的最坏参数组合,采用系统的开环尼克尔斯曲线验证了μ分析的结果;分析了系统所能容纳的最大不确定性参数,并研究了系统对不同不确定性参数的敏感性。结果表明:在密度、升力系数和阻力系数不确定性中,阻力系数对该标称轨迹的鲁棒稳定性影响最为明显。
μ分析; 不确定性; 再入; 线性分式变换
0 引言
高超声速飞行器是指马赫数不低于5的飞行器[1]。高超声速飞行器再入过程中,飞行包线大、飞行环境复杂、飞行高度及马赫数跨度大,气动特性变化剧烈;同时,由于缺乏足够的飞行试验,导致高超声速飞行器再入过程中存在很大的不确定性。因此,必须在各种不确定性存在的条件下,对设计的标称再入轨迹及制导律进行鲁棒稳定性评估。
在传统的制导稳定性评估中,常采用拉偏气动升阻和环境参数的方法,通过再入制导飞行仿真来确定再入轨迹及其制导律对主要不确定参数的适应性。工程上常采用的网格法将不确定性参数表达为参数不确定性并进行网格化,在网格点针对评估准则逐一评估。由于网格法仅在网格化的离散点进行评估,因此可靠性得不到保证;此外,其工作量会随不确定性参数的增加呈指数增加[2]。基于线性分式变换(Linear Fractional Transformation, LFT)的μ分析方法克服了网格法的不足,能在连续的频域范围内计算带有不确定性系统的结构奇异值,且其计算量是一个关于不确定参数个数的多项式函数[3]。
在采用μ分析方法进行鲁棒稳定性评估时,其可靠性很大程度上依赖于线性分式变换的质量。基于物理模型的建模方法(图操作方法)能充分考虑不确定参数之间的关联,避免了数值建模方法导致的保守性[4-5]。
1 模型建立
1.1三自由度纵向再入模型
在再入问题中,常应用瞬时平衡假设忽略姿态运动及地球自转,得到北天东坐标系中的高超声速飞行器三自由度纵向动力学方程[6],如式(1)所示:
(1)
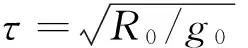
1.2基于物理模型的LFT建模方法
基于物理模型的LFT建模方法直接将不确定性参数引入飞行器非线性SIMULINK模型。以密度为例,假设密度可在其标称值附近±20%范围内变化,则密度可以表示为ρ=ρnom(1+WρΔρ)。其中ρnom为密度的标称值,Wρ值为0.2,Δρ∈[-1,1]。于是,包含不确定性参数的密度在模块中可以表示为如图1的形式,在密度不确定性处引入了一个虚拟输出zρ和虚拟输入wρ。这样,便直接将不确定参数引入到飞行器的非线性模型中,且由于考虑到了不确定参数之间可能存在的关联,不会引起数值建模方法带来的保守性问题[4,7]。

图1 基于物理模型的建模方法Fig.1 Modeling method based on physical models
1.3线性稳定储备准则
图2(a)所示的尼克尔斯图所对应的区域A和B分别对应±6 dB,±36.87°和±4.5 dB,±28.44°的储备要求。若系统的开环尼克尔斯曲线不穿越椭圆区域,则系统满足相应的幅值和相位储备要求[7]。由文献[8]可知,图2(b)中区域A和B分别对应奈奎斯特图中以-1.25为圆心、0.75为半径和以-1.14为圆心、0.54为半径的圆。系统的开环尼克尔斯曲线不穿越椭圆区域B,等价于系统的奈奎斯特曲线不穿越圆区域B。

图2 尼克尔斯椭圆区域和奈奎斯特圆区域Fig.2 Elliptical regions in Nichols plane and circular regions in Nyquist plane
在分析制导稳定性时,通过构造一个虚拟的复不确定块,将准则作为飞机对象虚拟的乘积型不确定性考虑,加入闭环系统。本文采用图2中区域B对应的储备准则。由文献[8-9]可知,所有包含评估准则的不确定对象的集合为:
(2)

(3)
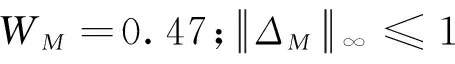
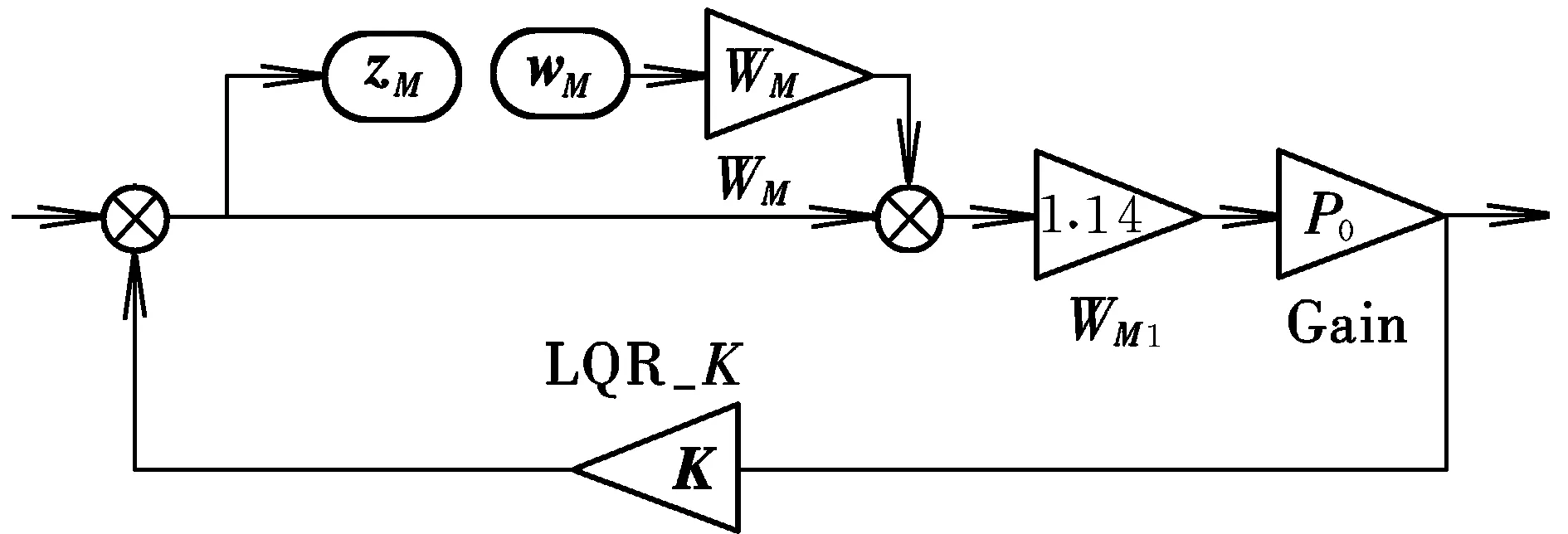
图3 引入幅值和相位裕度的反馈闭环系统Fig.3 Feedback closed-loop system with gain and phase margins introduced
2 结构奇异值理论
设结构Δ∈Cn×n为复数对角块,可描述为:
(4)
式中:S和F为重复标量子块和子满块的个数。
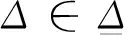
(5)
当不存在这样的摄动使det(I-MΔ)=0时,则定义μΔ(M)=0。
定理1:假设M∈RH∞,对于所有满足‖Δ‖∞≤1的Δ,图4所示系统鲁棒稳定的充要条件为:
(6)

图4 线性分式变换反馈框图Fig.4 Feedback block diagram of LFT
3 仿真计算及结果分析
3.1仿真计算
假设再入过程中密度、升力系数和阻力系数存在±20%不确定参数。按照基于物理模型建模原则搭建非线性动力学模型,并考虑±4.5 dB,±28.44°的线性稳定储备,利用Linmod函数可方便地得到含不确定性系统的状态空间实现。至此,便得到了关于密度、升力系数、阻力系数不确定参数的线性分式变换,且将线性稳定储备引入了原系统中。同时,复不确定参数的引入有效地解决了MATLAB无法计算实不确定参数的结构奇异值的上、下界的问题[11]。计算出的结构奇异值的上界可用于判断鲁棒稳定性,下界可用于确定“最坏情况”。
已知X-33的一条标称轨迹,相关的三自由度纵向状态信息和标称控制量如图5所示。

图5 X-33再入轨迹标称状态量和控制量Fig.5 Nominal statement profiles and control profiles of X-33 reentry trajectory
从σ剖面可以看出,再入过程中飞行器存在两次明显的翻转。翻转点也是再入过程中较为危险的点。本文以第一次翻转前后的状态点为例进行分析。
3.2鲁棒稳定性分析
假设ρ,CL和CD不确定性取值范围为[-20%,+20%],分别在r,V,γ和S2go通道加入线性稳定储备,得到第一次翻转前后状态点的结构奇异值频域响应如图6所示。由定理1可知,标称轨迹在给定不确定性参数摄动下满足鲁棒稳定性要求。

图6 第一次翻转前后结构奇异值Fig.6 μ values before and after the first bank-reversal
为了验证整条标称轨迹在制导律闭环后存在不确定参数时的鲁棒稳定性,可以更大范围地选取轨迹上的点进行验证。以r通道为例,其结果见图7。

图7 第一次翻转附近区域r通道结构奇异值Fig.7 μ values of r loop around the first bank-reversal point
结果表明,r通道的结构奇异值均小于1,说明标称轨迹r通道满足鲁棒稳定性要求。
3.3最坏情况验证
为了验证μ分析的结果,现以第一次翻转前状态点的r通道为例加以验证,其结果如图8所示。
由图8可知,在所求得的最坏情况下,系统的开环尼克尔斯曲线不穿越图2(b)中区域B所对应的稳定储备区域,即系统在密度、升力系数、阻力系数具有[-20%,+20%]不确定参数变化范围内的最坏情况仍满足鲁棒稳定性,从而验证了μ分析的结论。
3.4稳定性边界参数确定及“敏感性”分析
在对标称轨迹进行制导稳定性分析时,总希望求得其所能容纳的最大不确定性参数范围。现以第一次翻滚前r通道为例,在原有的20%基础上,按一定比例(在此选4%)同时增大3个不确定参数,其结构奇异值上界如图9所示。可以看出,随着不确定参数的增加,闭环系统的结构奇异值逐渐增加。当不确定参数达到约35%时,闭环系统临界稳定。
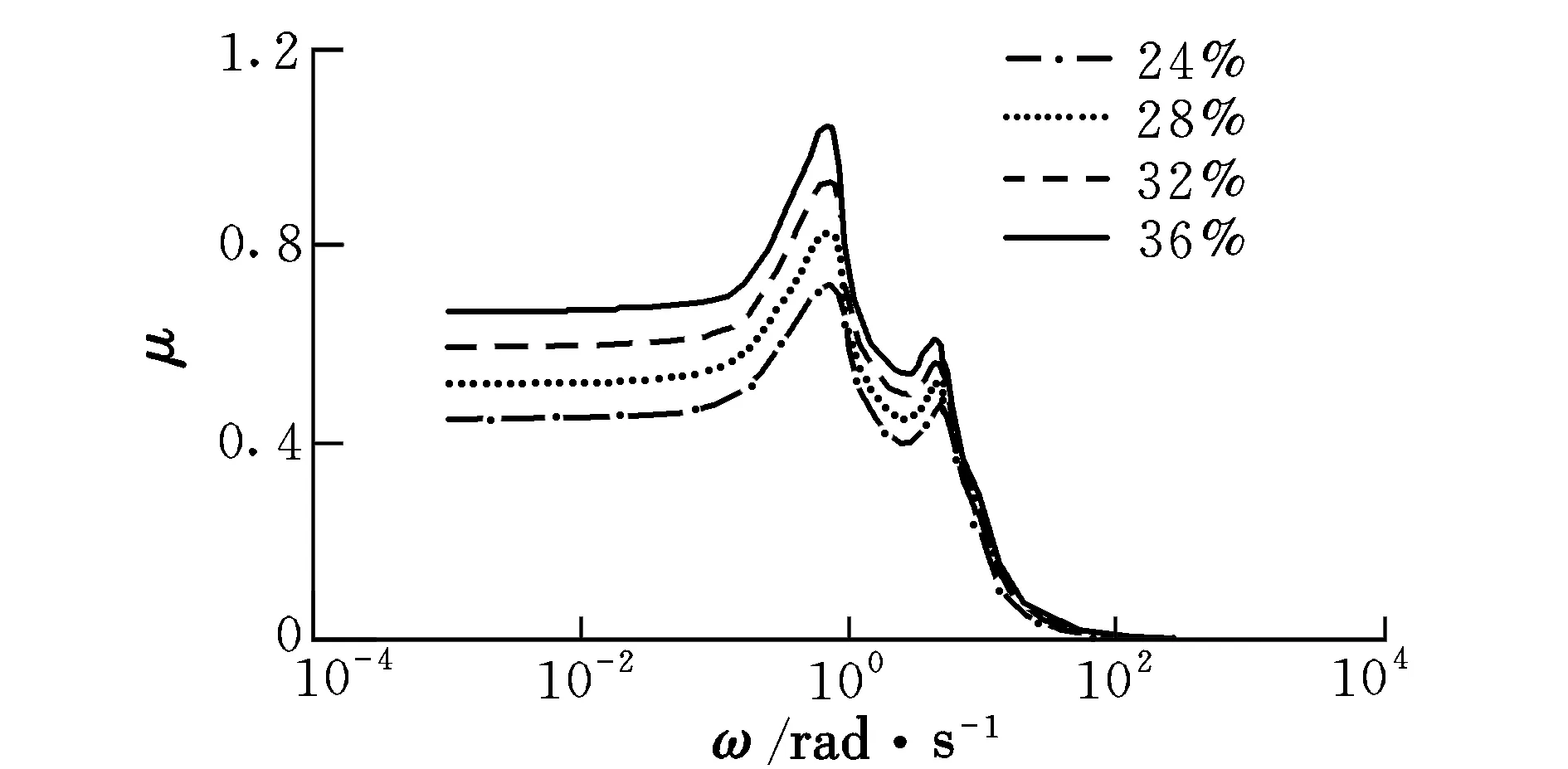
图9 不同不确定参数对应的结构奇异值上界Fig.9 The upper boundard of μ corresponding to different uncertain parameters
为了分析密度、升力系数、阻力系数三个不确定参数对闭环系统的标称轨迹稳定性的影响程度,在原有的20%不确定参数的基础上,固定其中两个不确定参数,增加另外一个不确定参数。通过计算系统的结构奇异值,来检验闭环系统的稳定性,从而分析不确定参数的“敏感性”,计算结果如图10所示。
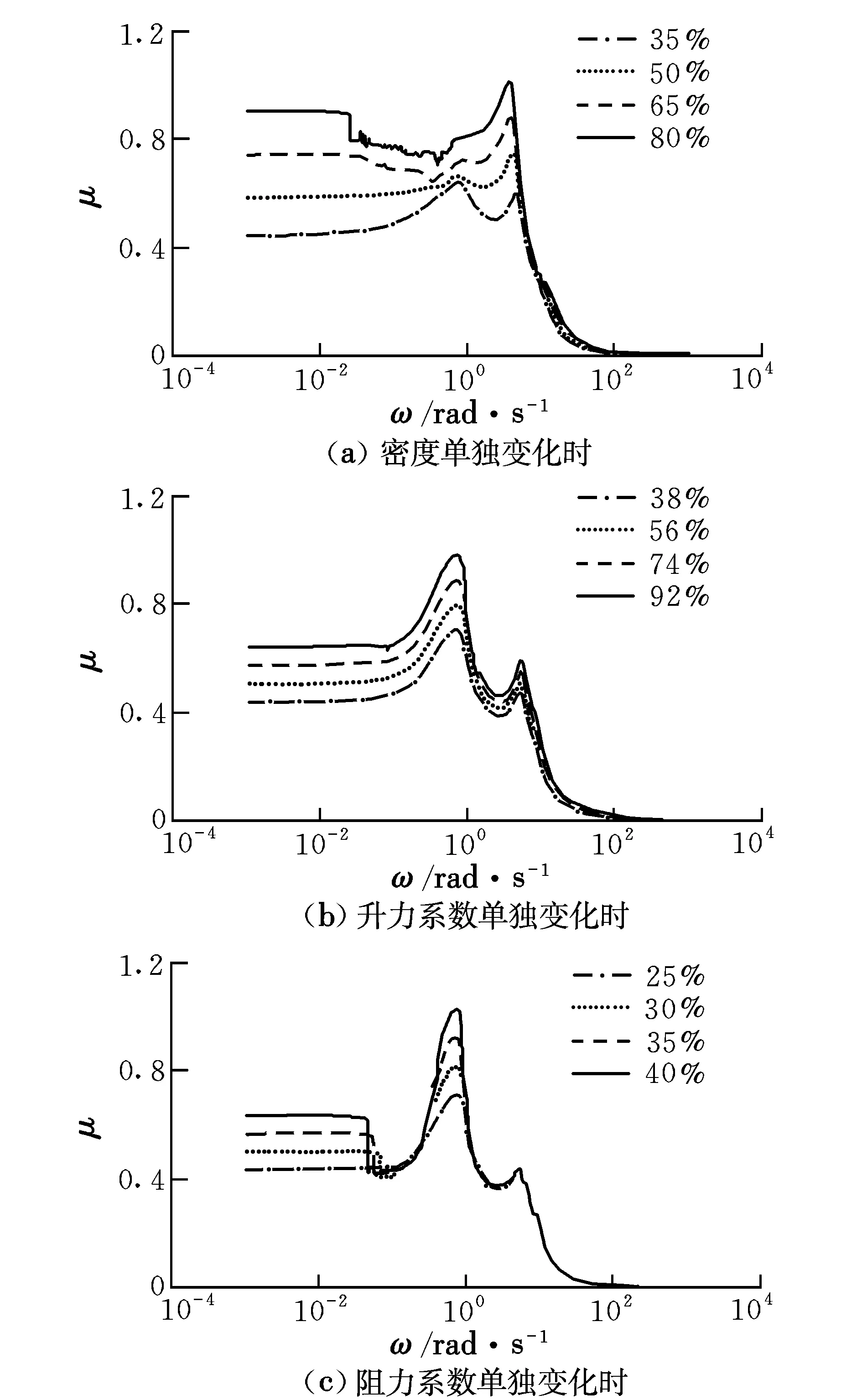
图10 不确定参数对系统稳定性的影响Fig.10 Influence of uncertain parameters on the system stability
由图10可知:当密度和升力系数不确定性分别达到80%和92%时,闭环系统临界稳定;而当阻力系数不确定性参数增加到40%时,闭环系统便失稳。因此可知,闭环系统的鲁棒稳定性对阻力系数不确定性参数更为敏感,因此在标称轨迹设计时需要着重考虑。
4 结束语
本文将结构奇异值理论应用到高超声速飞行器再入过程中存在参数不确定性时标称轨迹的鲁棒稳定性分析当中。应用该方法可对用不同方法设计的标称再入轨迹在存在参数不确定性时进行鲁棒稳定性分析,从而为高超声速飞行器再入轨迹的设计及制导律评估提供一定的参考。
[1]吴宏鑫,孟斌.高超声速飞行器控制研究综述[J].力学进展,2009,39(6):756-765.
[2]刘林.现代飞行控制系统的评估与确认方法[M].北京:国防工业出版社,2010:76-100.
[3]Juliana S.Re-entry flight clearance[M].Delft:Delft University of Technology,2006:15-18.
[4]Kureemun R,Bates D G,Hayes M J.On the generation of LFT-based uncertainty models for flight control law robustness analysis[R].AIAA-2001-4396,2001.
[5]Zerz E.LFT representations of parametrized polynomial systems[J].IEEE Transactions on Circuits and Systems,1999,46(3):410-416.
[6]Vinh N X,Busemann A,Culp R D.Hypersonic and planetary entry flight mechanics[M].MI, Ann Arbor:University of Michigan Press,1980:26-27.
[7]Bates D G,Kureemun R,Mannchen T.Improved clearance of a flight control law using-analysis techniques[J].Journal of Guidance,Control,and Dynamics,2003,26(6):869-884.
[8]Deodhare G,Patel V V.A "modern" look at gain and phase margins:anH∞/μapproach[R].AIAA-98-4134,1998.
[9]Kureemun R,Bates D G,Postlethwaite I.Quantifying the robustness of flight control systems using Nichols exclusion regions and the structured singular value [J].Proceedings of the Institution of Mechanical Engineers Part Ⅰ Journal of Systems and Control Engineering,2001,215(6):625-638.
[10]Kemin Zhou.Essentials of robust control[M].Louisiana:Louisiana State University,1999:165-220.
[11]Balas G J,Doyle J G,Glover K.MATLABμ-analysis and synthesis toolbox user’s guide[M].Version 3.USA:The Math Works Inc,1998:61-66.
(编辑:李怡)
Evaluation of re-entry trajectory of hypersonic vehicles based onμ-analysis
LI Wei-jie, SHEN Zuo-jun
(School of Aeronautic Science and Engineering, BUAA, Beijing 100191, China)
Theμ-analysis theory was applied to the evaluation of the nominal re-entry trajectory to solve the uncertainties in the course of re-entry of hypersonic vehicles. Based on the linear stability reserve criteria, the guidance stability of the nominal trajectory and guidance law was analyzed when the density, lift coefficient and drag coefficient are uncertainty. According to the worst-case combination of parameters, the Nichols curve of the open-loop system was used to verify the conclusion ofμ-analysis results. The maximum uncertainty parameters which the system could accommodate were analyzed, and the sensitivity of the system to different uncertain parameters was studied. The results indicate that the drag coefficient has the most obvious effect on the robust stability of the nominal trajectory in the uncertainties of the density, lift coefficient and drag coefficient.
μ-analysis; uncertainties; re-entry; linear fractional transformation
2015-09-14;
2016-01-06; 网络出版时间:2016-02-29 16:37
李伟杰(1991-),男,四川简阳人,硕士研究生,研究方向为高超声速飞行器制导与控制。
V412.4
A
1002-0853(2016)04-0050-04
