高超声速飞行器周期巡航轨迹设计与优化
2016-08-30徐文君陆宇平刘燕斌陈柏屹
徐文君, 陆宇平, 刘燕斌, 陈柏屹
(南京航空航天大学 航天学院, 江苏 南京 210016)
高超声速飞行器周期巡航轨迹设计与优化
徐文君, 陆宇平, 刘燕斌, 陈柏屹
(南京航空航天大学 航天学院, 江苏 南京 210016)
针对高超声速飞行器,给出了参数建模方法并分析了其气动特性,建立了乘波体外形高超声速飞行器的纵向平面运动学模型;提出了高超声速飞行器巡航段周期轨迹的方案及相应的轨迹优化方法。采用高斯伪谱法解决周期性轨道优化问题,将原有的连续周期非线性优化问题转化为多段离散优化问题,并采用SQP算法求得最优解。仿真结果表明,在巡航航程相同的情况下,周期轨迹比稳态轨迹更省燃料。
高超声速飞行器; 参数建模; 周期巡航; 高斯伪谱法
0 引言
高超声速飞行器由于在军事上具有部署时间短、打击精度高、突防能力强等优点,因此成为未来航空宇航科学发展的必然趋势。为了适应各种作战需求,人们对高超声速飞行器轨迹优化的要求越来越高。对于超燃冲压高超声速巡航飞行器,目前提出的方案均为由助推器将其加速到一定高度和速度,满足超燃冲压发动机工作条件后,转为超燃冲压发动机工作,进行高超声速巡航飞行。在巡航飞行段,一般采用固定高度、速度/航迹角的最优稳态巡航方案。然而早在1970年,研究人员就发现周期巡航比稳态巡航更省燃料。周期巡航轨迹方案由于存在势能和动能的转换,有利于获得最佳推进比,因此在固定航程的条件下可以更少地消耗燃料;在短航程内实现周期巡航轨迹的另一个优点是,飞行器可以灵活机动地执行各项临时任务,飞行轨迹难以预测,有利于实现精确打击和轨道变化跟踪。
Rudd等[1]认为,要实现长远范围的飞行,必须应用多样化周期轨迹方案。文献[2-3]均采用三角函数近似周期巡航轨迹,分别通过求解系数得到次优轨迹,并以此为初值求解燃料最省周期巡航轨迹。文献[4-5]利用直接法将周期轨迹优化问题转为非线性规划问题,从而获取最优周期巡航方案。
目前,国内研究的成果包括了常见的最优稳态巡航和单一的周期巡航方案。文献[6-8]针对不同的已知条件,分别用Newton-Raphson迭代法和遗传算法确定了高超声速飞行器周期巡航的条件,得出了只要满足特定条件,高超声速飞行器就可实现周期巡航且巡航初始值可在较大的范围内进行选择的结论。康炳南等[9]基于稳态动力学方程,采用 Powell优化算法求解了全局最优稳态巡航轨迹,随后考虑单周期的质量变化,利用非梯度优化算法进行最优周期巡航轨迹优化。马辉等[10]以高超声速飞行器为对象,利用Lagrange乘子法和共轭梯度法对最优周期巡航轨迹进行了研究,并给出了设计方法。
本文基于乘波体外形高超声速飞行器模型,采用SQP方法求解其稳态最优飞行状态,并以此为初值,运用高斯伪谱法求解周期巡航轨迹。总结出高超声速飞行器最优巡航轨迹优化的一般设计方法。
1 参数化模型
本文采用参数化建模的方法建立飞行器动力学模型,通过飞行器的几何外形特征参数集来计算飞行器的气动力和推力,最终推导出飞行器飞行动力学方程。整个建模过程主要分为几何建模、气动参数求解和推进系统建立三个部分。
几何建模采用类别形状函数变换参数化表示方法,通过对吸气式高超声速飞行器的前体压缩段、机身、控制面及超燃冲压发动机的几何外形进行参数化描述,建立的几何外形如图1所示。
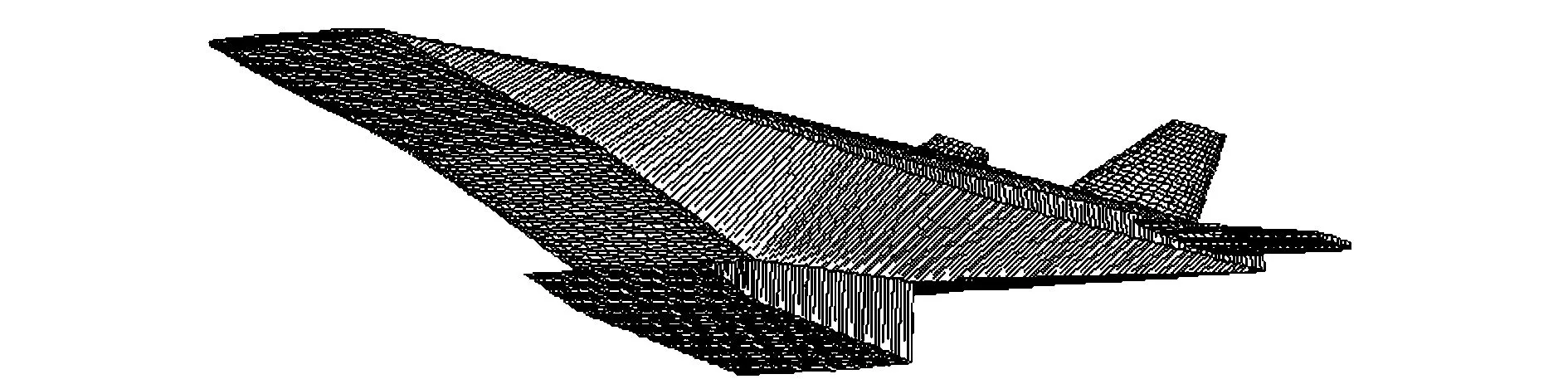
图1 飞行器几何外形Fig.1 Geometric profile of the vehicle
气动参数求解主要依据高超声速无粘流的基本理论,包括斜激波理论和膨胀波理论。通过对飞行器的几何外形进行面元离散化,进而根据S/HAP程序中独立面元假设的工程估算方法,计算并修正吸气式高超声速飞行器所受到的气动力。
推进系统建立采用准一维流假设,认为发动机流道内气流的参数仅为轴向距离的函数。推进模型由三部分组成:二维进气道压缩模型、隔离段/燃烧室模型和内/外喷管模型。采用变截面燃烧室以保证推进系统可以工作在超燃模态与亚燃模态。通过隔离段内的预燃烧激波串的建模,对超燃/亚燃过程进行仿真。内/外喷管采用变截面等熵流模型计算喷管出口处气流的速度与压强。进而根据进气道的空气质量流率与发动机入口的气流参数计算推进系统产生的推力。
2 巡航轨迹优化问题描述
高超声速飞行器巡航段垂直平面下的飞行动力学方程如下:
(1)
式中:H为飞行高度;V为飞行速度;γ为轨迹倾角;r为飞行航程;T为发动机推力;α为飞行器的迎角;L和D分别为升力和阻力;Re为地球半径;m为飞行器质量;g为地球引力常数。
2.1稳态巡航飞行
稳态巡航飞行定义为飞行器保持高度和速度不变的飞行状态,施加一定的控制量可以保证飞行器长时间稳定的巡航飞行。求解飞行器稳态飞行时的状态量和控制量是一个满足动态平衡和路径约束下实现燃料最省的优化问题。高超声速飞行器稳态飞行下最优状态(即单位距离的瞬时燃油率最小)的求解方法如下。
稳态飞行状态下,式(1)中前三项恒等于0,得出以下状态约束:
(2)
此外在稳态最优问题求解中飞行器应当保持配平状态,即力矩系数为0。
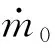
(3)
求解一组最优的飞行器飞行状态量和控制量,包括高度、速度、迎角、舵偏角和燃油当量比,使得飞行器在此飞行状态下的性能指标最大。
本文采用SQP算法解决离散非线性约束优化问题。SQP对于解决离散非线性优化问题来说是一种快速有效的优化方法,具有良好的全局收敛性和超线性收敛性,可以求解得到飞行器稳态飞行状态。
2.2周期巡航飞行
周期巡航飞行是指飞行器发动机按照一定周期进行开关操作,在周期结束时,飞行器的飞行状态量仍等于周期开始时的飞行状态。只要燃料足够,飞行器可以遵循一个周期内的飞行控制量,实现长远航程内的多个周期飞行。周期巡航飞行中的单个周期通常分为三段:滑翔段、推力段和滑翔段。根据初始条件的选择,第三段滑翔段可能省略;当飞行器初始动力不足时,第一段滑翔段的时间也可能优化为0。
高超声速飞行器的周期巡航飞行轨迹优化是一个连续多阶段非线性优化问题:优化一个周期内的飞行器控制量α(t),δ(t)和Φ(t),这里分别代表迎角、舵偏角和燃油当量比控制。将运动学方程(1)变换为以r为自变量的方程,周期巡航最优问题将满足以下的动力学方程约束:
(4)
起始和末端状态约束:
(5)
路径约束包括动压、过载和配平约束:
(6)
因此,周期巡航问题的性能指标描述为单个周期内消耗的燃料质量最少:
(7)
对于以上的多段连续非线性优化问题,本文采用多段高斯伪谱法求解。高斯伪谱法是一种成熟的算法,它可以将状态变量和控制变量在Gauss离散点上进行离散化,将原本的连续非线性优化问题转换为离散非线性问题,并且离散点满足所有约束条件,随后可以通过非线性序列二次规划求解。
3 飞行数值仿真
对于高超声速飞行器外形参数化建立的模型,可以在给定高度、速度、迎角和燃油当量比大小等飞行状态的条件下得到对应配平的舵偏角,随即获取飞行器气动力大小、推力大小和燃料消耗情况。假定发动机燃油当量比大小取1,目标高度30 km,升力、阻力、推力随迎角和速度的变化如图2所示。此外图2还给出了迎角为4°时,空气质量流率随高度和速度变化的曲面。
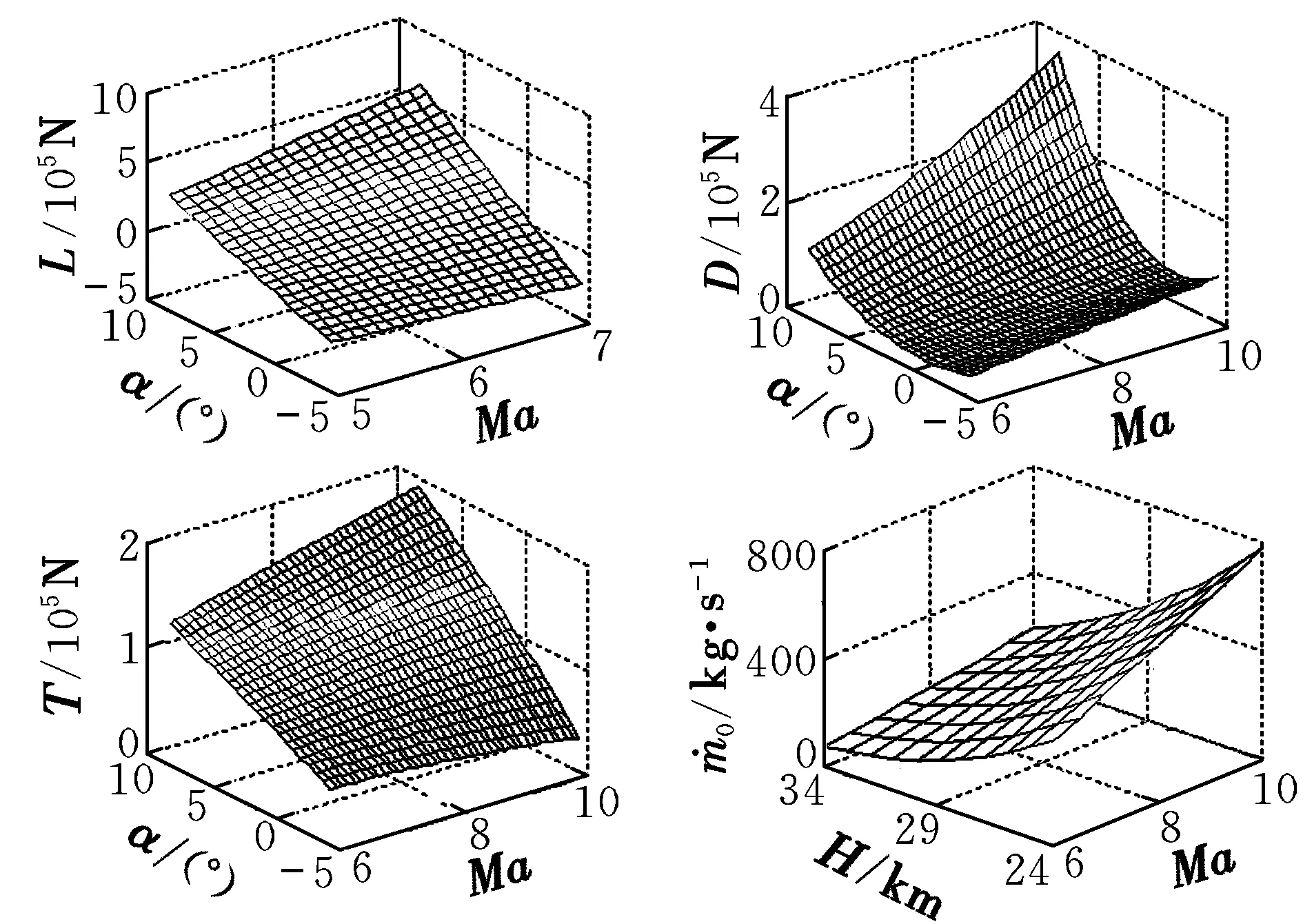
图2 升力、阻力、推力和空气质量流率的变化曲面Fig.2 Variation camber of L,D,T and
飞行器的质量设为22 094 kg,求解稳态巡航最优轨迹时设定优化变量x=[α,V,H,δ,Φ],利用前文中的等式约束和性能指标,同时限制高度在28~32 km,速度在1 800~3 000 m/s,迎角在-4°~8°的范围内,利用SQP算法求解。得到的最优解为x=[3.352 1°,2 121 m/s,32 km,3.976 6°,0.567 52]。即当飞行器以α=3.352 1°,V=2 121 m/s,H=32 km,δe=3.976 6°的状态稳态巡航飞行时,发动机燃油当量比大小设为0.567 52,此时单位距离的燃料消耗率最小,为0.001 321 1 kg/m。
在飞行器最优周期巡航轨迹优化时,首先选取上述稳态最优巡航轨迹的结果作为周期巡航状态的初始值猜测依据。选取航程在200 km左右,周期点的平均高度设定32 km,速度设定2 100 m/s,航迹倾角为0°,控制变量迎角设定在-4°~8°之间,舵偏角设定在-20°~20°之间,法向过载不超过5,气压不超过200 kPa,俯仰力矩时刻为0。推力段的油门控制在0~1之间。采用伪谱法作为优化算法,单个周期内的优化结果如图3所示。其中,实线代表周期最优轨迹,虚线代表稳态最优轨迹。
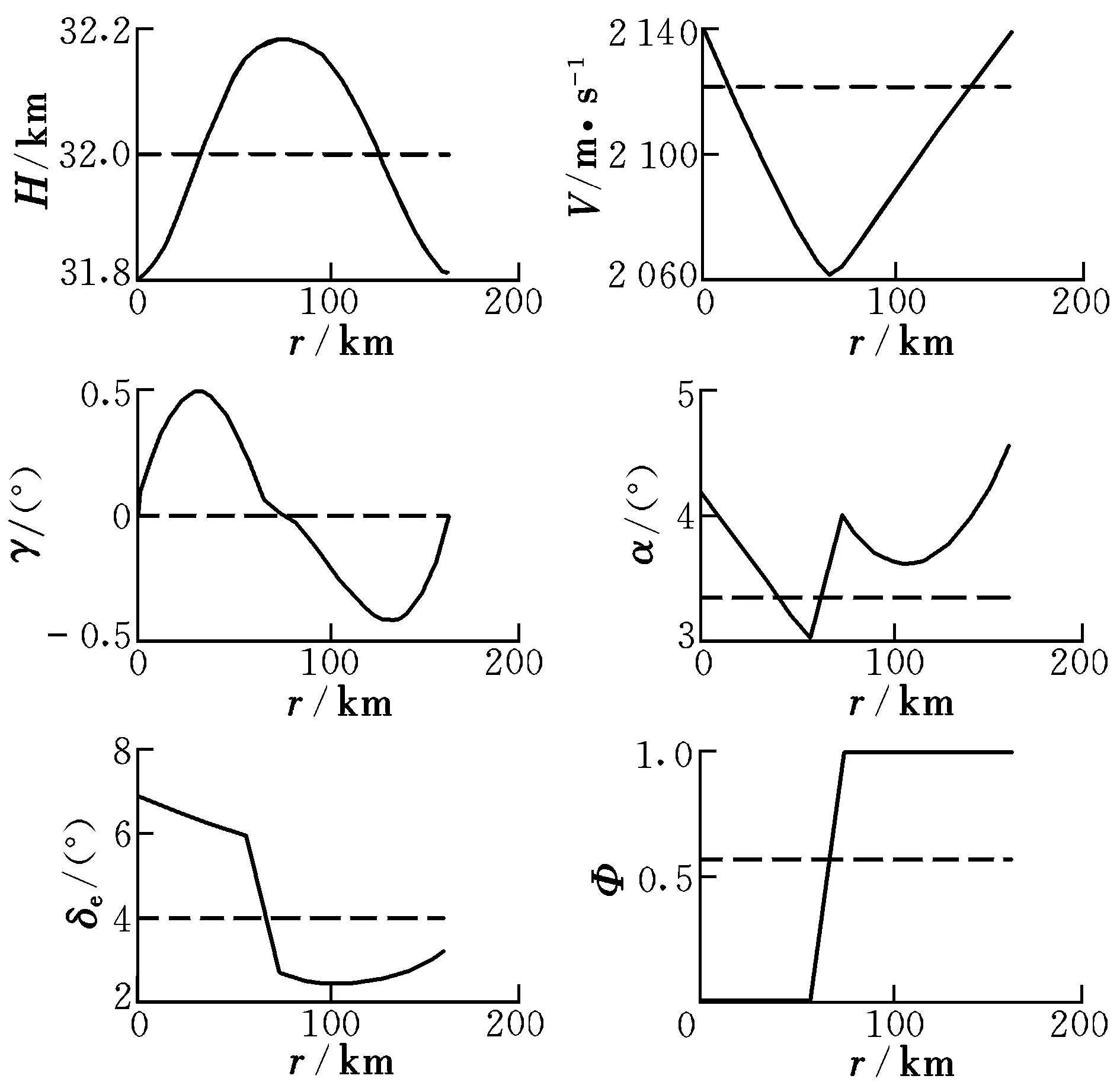
图3 周期巡航轨迹优化结果Fig.3 Results of the periodic cruising trajectory optimization
从图3中可以看出,高超声速飞行器的高度、速度、俯仰角等状态量均随着航程的增加呈现周期性的变化,整个周期航程为160 km,飞行时间约100 s。同时,图3分别给出了这一过程中迎角、舵偏角和发动机燃油当量比等控制量的大小。
优化结果是周期巡航轨迹的前一段为自由滑翔段,后一段为推力加速段。为了证实周期巡航轨迹的燃料消耗性能,将周期巡航与稳态巡航轨迹的燃料消耗率进行对比,如图4所示。
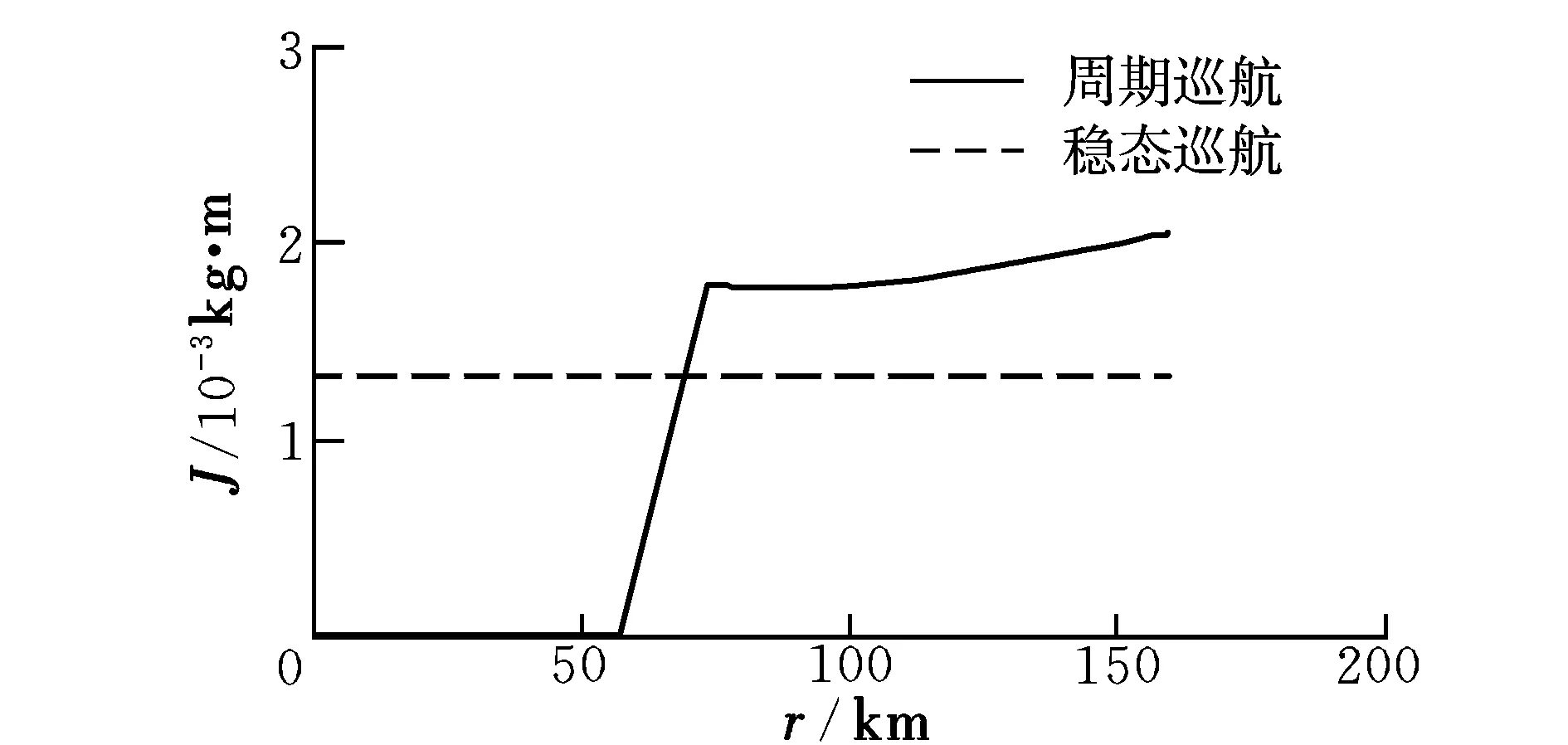
图4 燃料消耗率Fig.4 Fuel consumption rate
由图4可以看出,最终方案省略了一个滑翔段,即只需要滑翔段与推力段相互交替,就可以完成长远距离的周期轨迹巡航飞行。在单个周期巡航轨迹中状态量呈现周期性变化,发动机开关一次。
周期巡航方案对比稳态巡航方案优势很明显,基于本文建立的参数化外形模型,采用周期巡航飞行方案可节省17%的燃料。但具体节省燃料的多少还取决于任务要求及建立的燃烧室和推力模型。
4 结束语
本文经参数化外形后构建了高超声速飞行器的动力学模型。运用高斯伪谱法设计和实现了高超声速飞行器的周期最优轨迹求解,并比较了伪谱法下周期最优轨迹和稳态巡航轨迹的性能指标。仿真结果表明,周期巡航轨迹可以很大程度上减少空气质量流率,进而节省燃料。
[1]Rudd L V E,Pines D J,Ii P H C.Long-range performance of suboptimal periodic hypersonic cruise trajectories[J].Journal of Guidance,Control,and Dynamics,2000,23(4):756-758.
[2]Chuang C H,Morimoto H.Periodic optimal cruise for a hypersonic vehicle with constraints [J].Journal of Spacecraft and Rockets,1997,34(2):165-171.
[3]Wang H,Zhao D,Sun M.Optimization of periodic optimal cruise for a hypersonic vehicle [C]//Chinese Automation Congress (CAC).Changsha:IEEE,2013:571-576.
[4]Chen R H,Williamson W R.Optimization and implementation of periodic cruise for a hypersonic vehicle [J].Journal of Guidance, Control,and Dynamics,2006,29(5):1032-1040.
[5]Ngo A D.A fuel-optimal trajectory for a constrained hypersonic vehicle using a direct transcription method[C]//IEEE Aerospace Conference Proceedings (Vol. 4).Bigsky,MT:IEEE,2004:2704-2709.
[6]张忠峰,高云峰,宝音贺西.高超声速飞行器周期巡航与总体参数关系研究[J]. 导弹与航天运载技术, 2009(4):4-7.
[7]张忠峰,高云峰,宝音贺西.高超声速飞行器周期巡航条件的确定[J].力学与实践,2009,31(1):16-19.
[8]张忠峰,高云峰,宝音贺西.高超声速飞行器巡航燃料消耗分析[J].弹箭与制导学报,2009,29(1):184-187.
[9]康炳南,唐硕.有动力通用再入飞行器的轨迹设计与优化[J].航空学报,2009,30(4):738-743.
[10]马辉,袁建平,方群.高超声速飞行器最优周期巡航轨迹优化[J].飞行力学,2008,26(4):31-34.
(编辑:任亚超)
Design and optimization of periodic cruise trajectory for hypersonic vehicle
XU Wen-jun, LU Yu-ping, LIU Yan-bin, CHEN Bo-yi
(College of Astronautics, NUAA, Nanjing 210016, China)
In this paper, a parametric modeling method was given to analyze the aerodynamic characteristics of the hypersonic vehicle and to establish longitudinal dynamic model for wave rider-based vehicles. Then a periodic cruise trajectory optimization method for a hypersonic vehicle was proposed. Furthermore, Gauss pseudo-spectral method was applied in periodic orbit optimization problem by translating the original nonlinear optimization problem to a discrete optimization problem, and the optimal solution was obtained by using the SQP algorithm. Simulation results show that the periodic cruise trajectory can consume less fuel than the steady-state trajectory.
hypersonic vehicle; parameter modeling; periodic cruise; Gauss pseudo-spectral method
2015-09-07;
2016-01-31; 网络出版时间:2016-02-29 16:38
徐文君(1991-),女,江苏扬州人,硕士研究生,研究方向为高超声速飞行器控制、轨迹优化与跟踪等;
陆宇平(1957-),男,江苏扬州人,教授,博士生导师,研究方向为飞行器主动控制、景像匹配与精确制导等。
V249.1
A
1002-0853(2016)04-0033-04
