汽轮发电机计及双因素非线性影响的功角特性

康锦萍，　刘晓芳，　徐英辉，　王靖

(1.华北电力大学 电气与电子工程学院，北京 102206；2.中国电力科学研究院 计量研究所，北京 100192)



汽轮发电机计及双因素非线性影响的功角特性

康锦萍1，刘晓芳1，徐英辉2，王靖1

(1.华北电力大学 电气与电子工程学院，北京 102206；2.中国电力科学研究院 计量研究所，北京 100192)

为研究磁路饱和与磁场畸变双因素非线对汽轮发电机功角特性的影响，利用有限元方法获得发电机的有功和无功功角曲线，揭示计及双因素非线性的电抗随功角变化的规律，然后将分运行区间的饱和电抗用于功角特性解析法计算。研究结果表明，汽轮发电机计及双因素非线性后，极限功角小于90°，极限功率下降，无功功率减小；随着功角的增大，直轴电抗先增大后减小，交轴电抗变化不大，两者差值可达到14%；与直接用有限元方法计算的功角特性进行对比，用分运行区间电抗的计算结果非常吻合，而用空载特性修正的饱和电抗的计算结果相差较大。研究结果可为同步发电机静态稳定极限的确定和暂态稳定的判断提供参考。

汽轮发电机；磁路饱和；磁场畸变；功角特性；饱和电抗

0　引　言

同步发电机静态稳定极限的确定和暂态稳定的判断等电力系统关心的问题都离不开功角特性，但一般均采用不考虑饱和的功角特性。实际运行中发电机饱和程度随着运行工况的变化而改变，在某些非正常运行情况下，磁路饱和与磁场畸变程度要比额定运行状态严重的多，因此有必要研究磁路饱和与磁场畸变双因素非线性对功角特性的影响。

发电机的功角特性通常指有功功率随功角变化的关系。文献[1]给出受扰动后第一个振荡周期内发电机功角与有功功率之间的关系，并计算加速面积和减速面积，推导出实时判断发电机运行暂态稳定的方法。文献[2]给出用发电机工况参数模型来计算定子的端部温度，从而确定发电机在各种运行方式下的进相运行能力及PQ容量图。文献[3]用有限元方法计算了高压发电机在额定电压和额定励磁电流时的功角特性，并研究分析其基本电抗随功角变化的关系。文献[4-6]有限元方法研究了磁路饱和对同步发电机的功角特性的影响。

大部分文献都是针对发电机的有功功角特性进行研究，实际上发电机功角的改变也会引起无功功率的改变。陈磊等[7]指出发电机作为电力系统中主要的动态无功电源，其发出无功功率是否达到极限对维持系统电压稳定性至关重要。发电机进相运行可解决电力系统无功过剩问题，文献[8]研究了发电机进相运行对系统静态稳定极限的影响。文献[9]建立同步发电机无功容量曲线的一种可视化工具，方便研究不同参数变化对其的影响。文献[10]提出用发电机无功容量曲线来同时分配有功和无功负荷的方法。文献[11]以发电机安全运行极限为基础，根据无功输出能力把发电机运行域分为不同区域来计算无功容量费用。文献[12]对比研究高压电缆绕制的发电机有功和无功功角特性。文献[13]用数值分析法研究了凸极同步发电机静态稳定极限功率和极限功角随试验电压及电气参数的变化规律。可见发电机无功功率功角特性对于电力系统运行和稳定同样重要。

本文以300 MW汽轮发电机为对象，采用有限元方法，研究端电压为额定值时磁路饱和与磁场畸变双因素非线性对有功和无功功角特性的影响，并获得了计及双因素非线性的电抗及其随功角的变化规律，进一步将该电抗用于有功功角特性和无功功角特性的分析，为电力系统稳定分析提供准确依据。

1　计及双因素非线性影响的功角特性

1.1磁场畸变

文献[14]指出同步发电机的非线性特征会受到磁路饱和与磁场畸变双因素非线性共同作用的影响。图1给出300 MW汽轮发电机额定电压下功角75°的磁场分布图。图中定子阴影部分表示磁导率μFe<50μ0的区域，转子阴影部分表示磁导率μFe<20μ0的区域。

图1　δ=75°时的磁场分布图Fig.1　Magnetic distribution when δ=75°

从图1可以看出，功角75°时合成磁场轴线偏向于q轴，转子小齿大部分单元的磁导率都小于20μ0，达到高度饱和，此时磁力线不是沿半径方向穿过气隙，而是斜穿定转子槽，磁力线所走的等效气隙长度[15]为0.312 m(实际上气隙长度为0.15 m)，磁场发生了畸变。

1.2计及双因素非线性影响的功角特性

同步发电机的功角特性可用公式(1)计算，若为隐极发电机，有Xd=Xq。发电机同步电抗通常采用制造厂给定的不饱和值。

(1)

图2给出300 MW汽轮发电机额定电压UN和额定励磁电流IfN时的有功功率功角特性，其中不计双因素的功角特性用公式(1)计算，计及双因素的功角特性采用1.3节的有限元方法计算。

从图2可以看出，计及双因素非线性后极限功率和极限功角都有所减小，计及非线性的极限功率比不计非线性的值小1.21%，极限功角从90°变为85°。

表1给出300 MW发电机额定电压UN下不同励磁电流时的极限功率及极限功角。

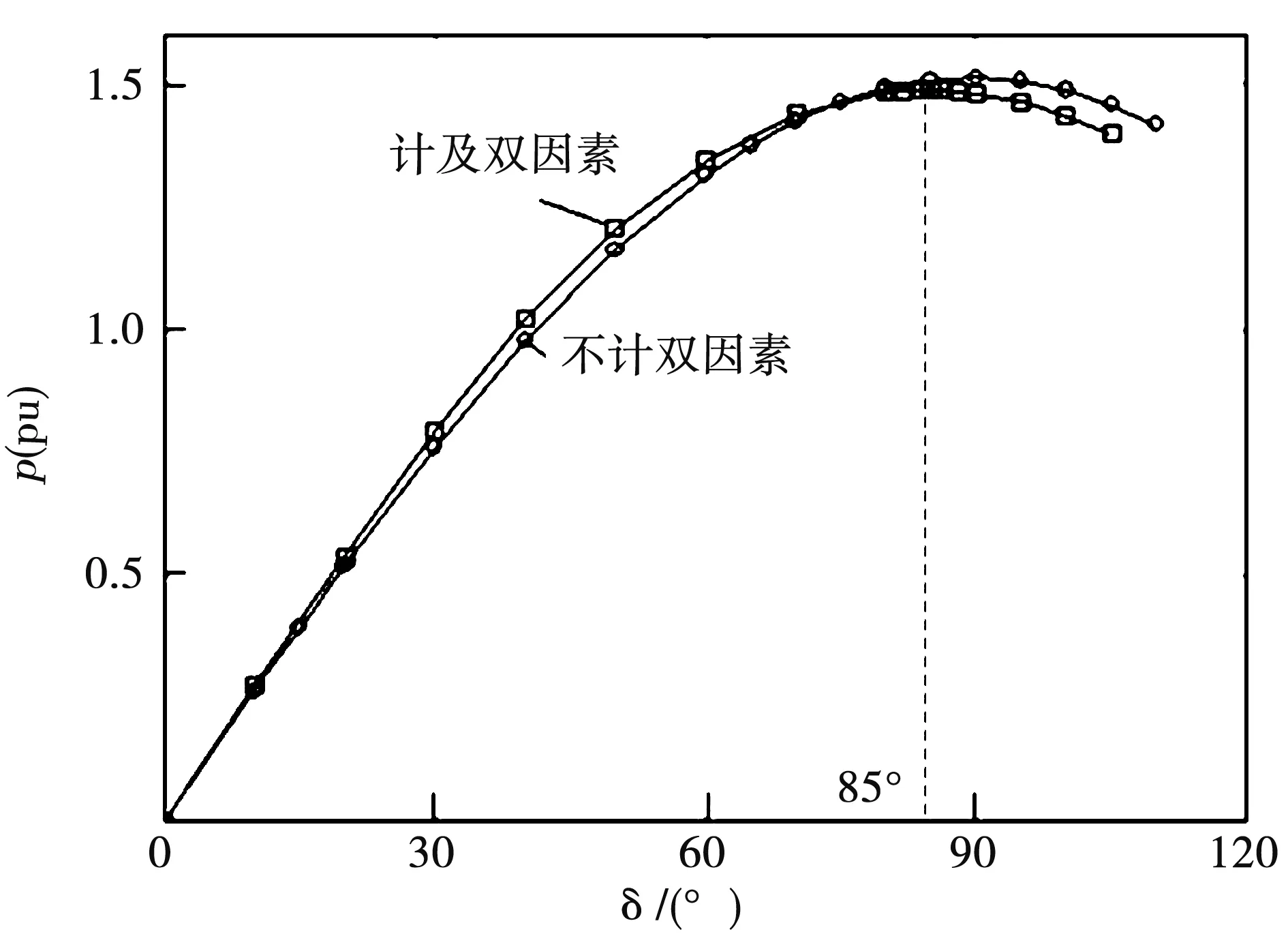
图2　U=UN,If=IfN时的有功功角特性Fig.2　Active power angle characteristic under U=UN,If=IfN

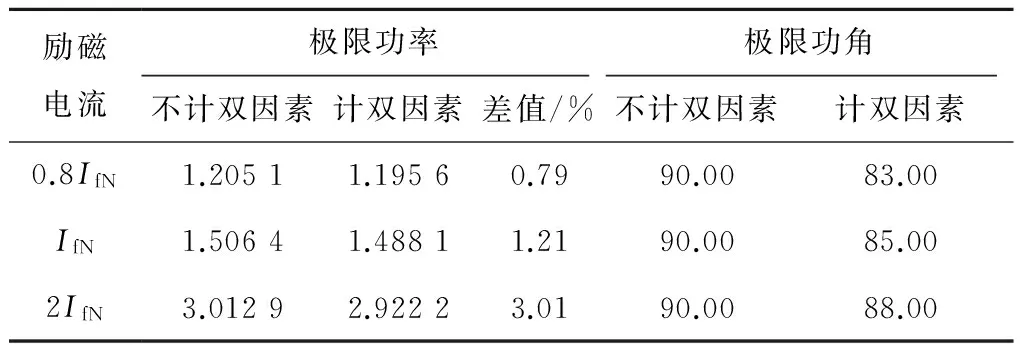
励磁电流极限功率极限功角不计双因素计双因素差值/%不计双因素计双因素0.8IfN1.20511.19560.7990.0083.00IfN1.50641.48811.2190.0085.002IfN3.01292.92223.0190.0088.00

从表1可以看出，不论励磁电流的大小，只要计及双因素非线性后，极限功率和极限功角都比不计非线性的值要小。随着励磁电流的增大，双因素非线性对极限功率的影响增大，极限功角却越来越接近于90°。

图3给出300 MW汽轮发电机额定电压UN和额定励磁电流IfN时的无功功率功角特性。

图3的计算结果表明双因素非线性对无功功率功角特性影响较大，两种情况下的特性曲线有明显差异。当功角为0°时，不计双因素非线性发出的无功功率为0.755，计及双因素非线性发出的无功功率为1.050，两者相差28%；发出无功功率为0的角度也存在很大不同，两者相差12.1°。

1.3基于有限元的功角特性的计算方法

为了计及磁路饱和与磁场畸变双因素非线性对功角特性的影响，可用有限元分析法进行磁场计算。当励磁电流If和端电压U确定时计算功角特性步骤如下：

1)给定某一小功角δ，给出电枢电流I和相位λ的初值进行磁场计算，得到端电压Unew和功角δnew；

3)计算有功功率P=UIcosФ和无功功率Q=UIsinФ；

4)增大功角δ=δ+△δ，返回步骤1)进行下一功角的计算，直到算出功角特性。

图3　U=UN,If=IfN时的无功功角特性Fig.3　Reactive powercharacteristic under U=UN,If=IfN

2　计及双因素非线性影响的电抗

2.1计及双因素非线性影响的电抗的计算方法

发电机饱和电抗的计算方法传统用空载特性得到饱和系数修正不饱和电抗得到。为了充分考虑负载运行条件的不同，后来发展到用有限元方法直接计算饱和电抗。IEEE[17]中给出用现场测量数据来获取饱和电抗的方法，发电机端电压U、定子电流I、励磁电流If、功率因数cosφ、功角δ等量都可以测出，这样就可画出图4所示的凸极发电机考虑饱和时的相量图，图中电抗Xds和Xqs都是饱和值。

图4　凸极发电机考虑饱和时的相量图Fig.4　Saturated phasor diagram of salient pole generator

图4中d轴方向上有

(2)

图4中q轴方向上有定义

(3)

发电机有限元磁场的二维数学模型能很好地考虑发电机磁路饱和与磁场畸变双因素非线性。文献[18 ]用有限元方法计算了发电机的励磁电流，并与实测值对比，所有误差都小于2%，验证了有限元方法的准确性。如果没有实测数据，可以用有限元方法计算公式(2)和式(3)中所需要的发电机电气量，从而得到能计及双因素非线性的电抗。

2.2汽轮发电机计及双因素非线性的电抗

图5给出300 MW汽轮发电机额定电压UN和额定励磁电流IfN时，饱和电抗X随功角δ变化的关系，其中基于空载特性的饱和电抗Xc是用空载特性修正制造厂给的不饱和值得到，计及双因素的Xd和Xq是用有限元方法和公式(2)和式(3)计算得到。图6给出图5运行状态下的气隙电势Eδ随功角δ变化的关系。

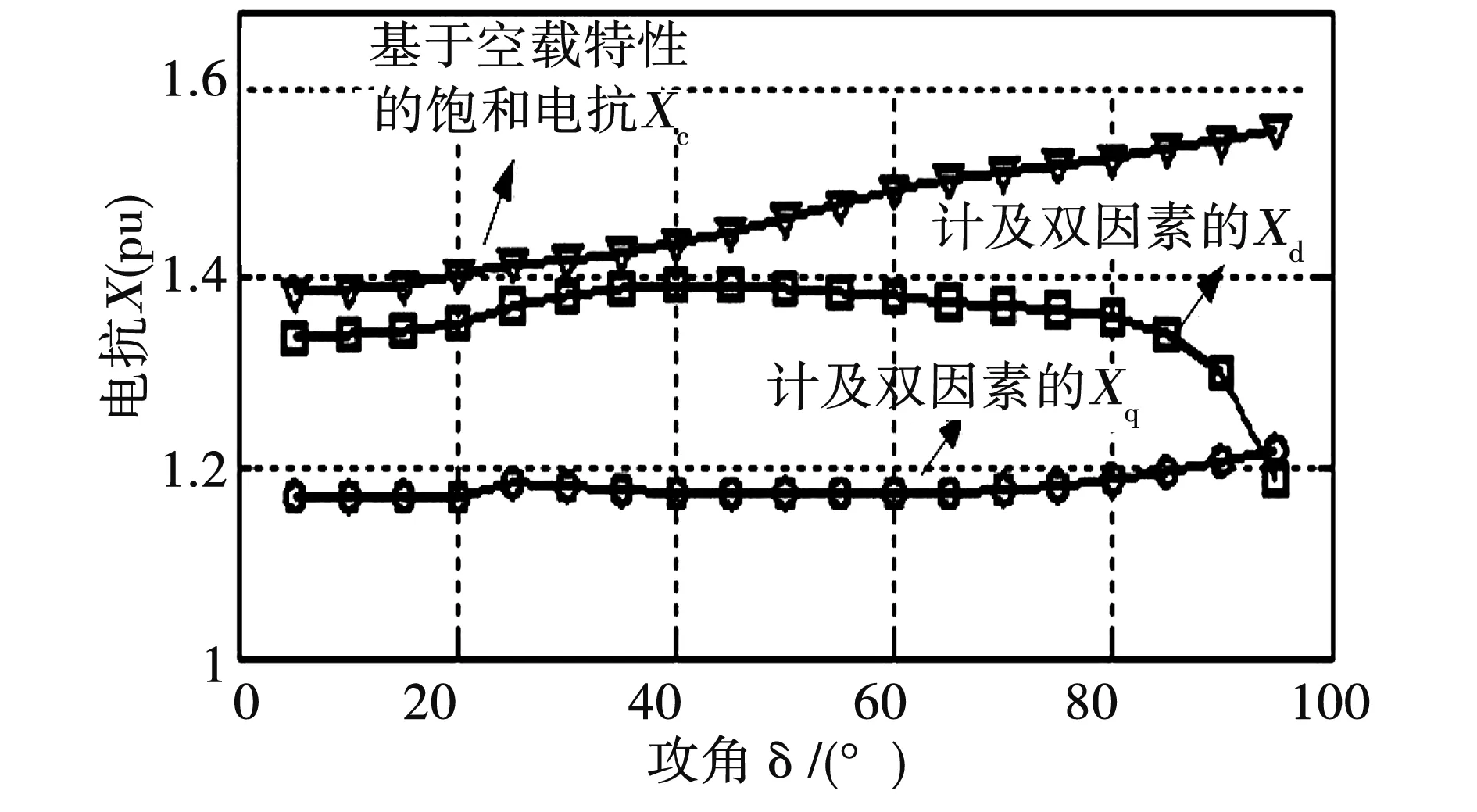
图5　不同功角下的饱和电抗Fig.5　Saturated reactances when different angles

从图6可以看出，当端电压和励磁电流固定时，随着功角的增大，气隙电势Eδ下降，主磁路饱和程度下降，因此图5中用基于空载特性饱和电抗Xc随着功角的增大而增大，且不考虑隐极发电机d轴和q轴的差异；实际上，随着功角的增大，主磁路饱和程度虽然下降，但磁场畸变程度使得等效气隙增加，这样就导致饱和电抗的变化不是单调上升的，如图5所示计及双因素电抗Xd，当功角小于40°时，主磁路饱和占主导地位，Xd有所上升，从1.33增加到1.39，增加了4.51%，当功角继续增大，磁场畸变占主导地位，Xd又下降，从1.39 减小为1.30，减小了6.47%。电抗Xq介于1.17～1.19～1.20之间，变化较小。

图6　不同功角下的气隙电势Fig.6　Air gap potential when different angles

3　基于双因素非线性电抗的功角特性

1.2节的计算结果表明发电机双因素非线性对发电机极限功角和无功功角特性有一定影响。因此计算功角特性时最好采用能计及双因素非线性的电抗。表2给出图5所示的不同功角范围内平均饱和电抗，表中最后1列为用空载特性修正的饱和电抗。

表2　分区间的平均饱和电抗

将表2的分区间饱和电抗代入功角特性公式(1)计算，其中E0=XadsIf=(Xds-Xσ)If，xσ取常数，并与直接用有限元计算的功率进行对比，两种方法计算的有功功率绝对差值△P如图7所示，△P都很小。同样用两种方法得到的无功功率绝对差值△Q也很小。可见分区间饱和电抗能很好地反应双因素非线性的影响。

图8(a)和图8(b)分别给出300 MW发电机用表1中分段饱和电抗代入公式(1)计算的有功和无功功角特性。

从图8可以看出，用计及双因素电抗计算的功角特性与用基于空载特性电抗计算的特性之间有较大差异，说明空载特性不能很好表征不同运行条件下的非线性特性。图7计算结果指明计及双因素的电抗计算的功角特性与直接用有限元方法的计算值几乎相等。可见基于双因素非线性饱和电抗的功角特性能更准确表征发电机的非线性特征。

图7　两种方法计算的有功功率之差△PFig.7　Active power differences between two methods

图8　基于饱和电抗计算的功角特性Fig.8　Power angle characteristics based on saturated reactances

4　结　论

文中以有限元方法为工具，以300 MW汽轮发电机为对象，研究磁路饱和与磁场畸变双因素非线性对发电机功角特性及参数的影响，得到结论如下：

1)汽轮发电机计及双因素非线性后，不论励磁电流的大小，极限有功功率都有所降低，极限功角都小于90°，无功功角特性与不计非线性的特性之间有较大差异。

2)当发电机端电压和励磁电流固定时，随着功角的增大，气隙电势降低，用空载特性修正得到的饱和电抗单调增加，而计及双因素的直轴电抗先上升后下降，交轴电抗变化较小。

3) 提出用计及双因素非线性的分区间饱和电抗计算功角特性的方法，该方法能很好表征不同功角时磁路饱和与磁场畸变对非线性特征的影响，与直接用有限元方法计算结果几乎重合在一起。

本文仅以1种典型汽轮发电机为研究对象，可以进一步扩展到多种汽轮发电机和水轮发电机，寻找适合电力系统使用的能计及发电机复杂非线性的功角特性，为电力系统准确分析提供依据。

[1]刘广健，卢继平. 基于功角特性曲线的发电机运行状况实时分析 [J]. 电网技术，2006，30：41-45.

LIU Guangjian, LU Jiping.Real-time analysis of generator operation state based on power-angle curve [J]. Power System Technology, 2006，30：41-45.

[2]史家燕，史源素，赵肖敏，等. 发电机工况参数模型及进相运行在线监测 [J]. 中国电机工程学报，2006，26(11)：139-143.

SHI Jiayan,SHI Yuansu,ZHAO Xiaomin,et al．The new method of determining the capability of leading phase of generator and realizing the on-line monitoring [J]. Proceedings of the CSEE, 2006，26(11)：139-143.

[3]GE baojun, LIN Peng, TAO Dajun. et al. Calculation and analysis of saturated power angle characteristic and reactances variation for new high voltage generator[C]//2009 International Conference on Sustainable Power Generation and supply.Nanjing,China,April 6-7,2009:2312-2316.

[4]姚有光，汤蕴璆. 凸极同步电机饱和功角特性的数值计算[J]. 哈尔滨电工学院学报，1987，10(1):9-15.

YAO Youguang, TANG Yunqiu, Numerical calculation of saturated power angle characteristics of salient pole synchronous machine [J]. Journal of Harbin Institute of Electric Technology,1987，10(1):9-15.

[5]ZHOU Ji, LUO Yingli, CUI Xiang. Determination of power-angle curves of synchronous machines considering cross-magnetizing saturation effect [C]//Proceedings of 2000 IEEE PES Winter Meeting，Singapore，20001:228-232.

[6]史家燕，董明会，李惠升，等. 汽轮发电机的饱和功-角特性 [J]. 中国电机工程学报，1986，6(3):1-7.

SHI Jiayan, DONG Minghui, LI Huisheng, et al.Saturated power angle characteristic of turbogenerator [J]. Proceedings of the CSEE, 1986, 6(3):1-7.

[7]陈磊，闵勇. 发电机无功极限诱导分岔的机理分析及预防策略 [J]. 中国电机工程学报，2008，28(10)：14-19.

CHEN Lei, MIN Yong,Mechanism analysis and preventive measures investigation of generator reactive power limit induced bifurcation [J]. Proceedings of the CSEE 2008，28(10)：14-19.

[8]牟童，宋丹，叶峰. 计及静稳极限的发电机进相运行能力研究 [J]. 东北电力技术，2010，10：7-11.

MAO Tong, SONG Dan,Capability study on generator leading operation considering static stability limit [J]. Northeast Electric Power Technology，2010，10：7-11.

[9]P. da Costa Jr., A. Nunes de Souza, P. S. da Silva,et. A Visual tool for building synchronous generator capability curves[C]//2012 Proceedings of IEEE Southeastcon, Orlando, Florida, USA, 15-18 March 2012: 1-6.

[10]XU Cheng，Frederick C. Huff，Peter Francino. Optimal load dispatch based on generator reactive capability curve[C]//IEEE Power Engineering Society General Meeting, 18-22 June 2006, Montreal, Quebec, Canada,2006: 22-26.

[11]余娟，颜伟，李文沅. 考虑发电机安全运行极限的非固定分段无功优化模型及其算法 [J]. 中国电机工程学报，2007，27(7)：23-28.

YU Juan, YAN Wei, LI Wenyuan.An Unfixed piecewise podel of reactive optimization and its algorithms considering generator capability limits [J]. Proceedings of the CSEE, 2007，27(7)：23-28.

[12]TAO Dajun, GE Baojun, LÜ Yanling, et al. Systematically study on the static power-angle characteristics of a high voltage cable-wound generator prototype[C]//2009 International Conference on Sustainable Power Generation and supply. Nanjing,China,April 6-7, 2009:2236-2240.

[13]李志强， 何凤军， 晁晖. 进相试验中凸极同步发电机静态稳定限制的数值分析 [J]. 电机与控制学报， 2011，15(12):89-94.

LI Zhiqiang, HE Fengjun, CHAO Hui.Numerical analysis of steady state stability limit of salient synchronous generator in leading power factor operation test[J]. Electric Machines and Control, 2011, 15(12):89-94.

[14]罗应立，蒙亮，刘晓芳，等．汽轮发电机双因素非线性特性的研究 [J]．电工技术学报，2005，20(6)：1-15

LUO Yingli，MENG Liang，LIU Xiaofang，et al．Study of two factors affecting nonlinear characteristic of turbogenerator [J]．Transactions of China Electrotechnical Society，2005，20(6)：1-5.

[15]张新丽，罗应立，康锦萍，等. 汽轮发电机内部非线性特征的定量表述 [J]. 中国电机工程学报，2007，27(24) ：74-78.

ZHANG Xinli，LUO Yingli，KANG Jinping，et al. The quantitative description of the nonlinear phenomena of the turbo-generator[J]．Proceedings of the CSEE，2007，27(24)：74-78．

[16]李志强，胡笳，祝丽芳，等. 同步发电机有限元磁场计算中端点量迭代的改进算法 [J]. 电工技术学报, 2008，23(12):35-41.

LI Zhiqiang, HU Jia,ZHU Lifang,et al. An improved iterative algorithm for terminal quantity of synchronous generator in FEM magnetic field [J].，Transactions of China Electrotechnical Society 2008, 23 (12) :35-41.

[17]IEEE Std 115-1995,IEEE Guide for Test Procedures for Synchronous Machines[S].

[18]康锦萍，刘晓芳, 罗应立，等. 不同容量汽轮发电机负载非线性特性的对比研究 [J]. 中国电机工程学报，2009，29(24):73-77.

KANG Jinping, LIU Xiaofang, LUO Yingli, et al．Research on the nonlinear load characteristics of different capacity turbine generators [J]. Proceedings of the CSEE，2009，29(24):73-77.

(编辑：刘素菊)

Power angle characteristic of turbine generator considering two factors affecting nonlinear characteristics

KANG Jin-ping1,LIU Xiao-fang1,XU Ying-hui2,WANG Jing1

(1. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China;2. Metrology Department, China Electric Power Research Institute, Beijing 100192, China)

To study power angle characteristic of turbine generator considering two factors of iron saturation and magnetic field distortion affecting nonlinear characteristics, active and reactive power angle curves were obtained by the finite element method. The variation laws of saturated reactances considering two factors nonlinearity were revealed and these saturated reactances divided into different operating regions were used to analytical expressions of power angle curve. The research results show that power angle limit of turbine generator considering two factors is less than 90 degree and active power limit and reactive power are reduced. The direct reactance increases at first and then decreases with increase of power angles and quadrature reactance changes smaller and their differences are up to 14%. Comparing with power angle curves by finite element method(FEM), calculation results with saturated reactances in different operating regions are in good agreement and values with reactances based on no-load characteristic are very different.The research results can provide references for analyses of steady-state stability limit and transient stability.

turbine generator；iron saturation；magnetic field distortion；power angle characteristics；saturated reactance

2014-11-21

国家自然科学基金(51307049)

康锦萍(1975—)，女，博士，副教授，研究方向为电机的磁场分析；

刘晓芳(1961—)，女，教授，研究方向为电机运行与控制；

康锦萍

10.15938/j.emc.2016.08.003

TM 341

A

1007-449X(2016)08-0017-06

徐英辉(1972—)，男，硕士，高级工程师，研究方向为电气测量与电机节能方面；

王靖(1971—)，女，硕士，讲师，研究方向为电机运行及故障诊断。