具备视角协同学习能力的多视角TSK型模糊系统

程　旸　顾晓清　蒋亦樟杭文龙　钱鹏江　王士同（江南大学数字媒体学院无锡214122）



具备视角协同学习能力的多视角TSK型模糊系统

程旸顾晓清蒋亦樟*杭文龙钱鹏江王士同
（江南大学数字媒体学院无锡214122）

传统模糊系统建模方法本质上是一种单视角学习模式，面向适合多视角处理的场景时，它们通常只能将每一视角割裂开来进行独立建模，这导致其所得系统泛化性能往往不令人满意。针对此缺陷，该文探讨具备多视角学习能力的模糊系统建模方法。为此，基于经典的L2型TSK模糊系统，通过引入具备多视角学习能力的协同学习项，该文提出了核心的多视角TSK型模糊系统（MV-TSK-FS）建模方法。MV-TSK-FS不仅能有效地利用各视角不同特征构成的独立样本信息，还能充分地利用各视角间由于相互关联而存在内在信息，以最终达到提高系统泛化性能的效果。在模拟数据集与真实数据集上的实验结果验证了较之于传统单视角模糊建模方法该多视角模糊系统有着更好的泛化性和适用性。

多视角学习；协同学习；模糊建模；TSK型模糊系统

模糊系统作为智能计算领域重要的研究分支，其独特的可解释性以及强大的学习能力，得到了较广的应用［9，10］。传统的模糊系统建模方法均采用单视角学习方式，其在面对多视角问题时，一般的处理方式是人为地将多视角样本集根据不同的视角划分成若干个独立的样本，然后根据每一视角的样本构建出专属于该视角的模糊系统。这种模糊系统存在各视角模糊系统泛化能力低且各视角间的系统泛化性能良莠不齐的现象。造成上述影响的主要原因在于单视角的建模方法只是简单地根据每一视角的样本的独立性特征构建出了适应于该视角的模糊系统而无视了各视角样本之间的关联关系，使得多视角样本集的特征无法得到充分的利用，从而导致了上述现象。

针对上述挑战，本文提出了一种具有多视角学习能力的模糊系统建模方法。鉴于Takagi-Sugeno-Kang（TSK）［11］型模糊系统在面对中小规模数据建模时优越的性能，本文将其作为具体研究对象来构建多视角模糊系统。在此模型的基础上，通过引入多视角学习机制，构造出了新的目标函数，使得该模糊系统不仅能够考虑各视角的独立信息还能够考虑各视角间的关联信息，进而达到提升系统泛化能力及稳定各视角间系统性能的目的。各行各业科学技术的发展正在日益变化，看待问题的方法及角度也越来越丰富，这使得本文所提出的多视角TSK型模糊系统具有较好的应用前景。

2　传统的TSK型模糊系统

经典模糊系统模型可分为以下3类：TSK型模型［11］，Mam dani-Larsen（ML）型模型［12］及广义模糊模型（Generalized Fuzzy Model，GFM）［13］。其中，TSK型模型应用最为广泛［11］。在本节中我们将对传统TSK型模糊系统及其对应的学习策略进行简要的回顾。

2.1 TSK型模糊系统的基本概念

TSK型模糊系统的模糊推理规则可表达为

TSK型模糊系统在去模糊化后其最终输出可表示为

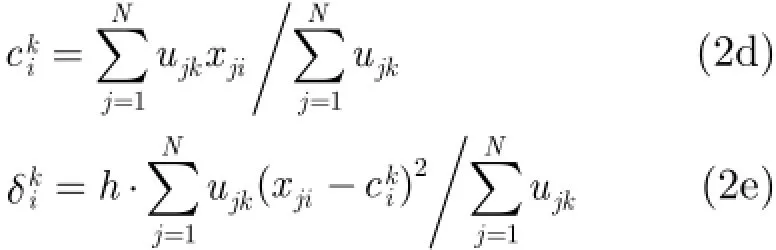
式中，jku即通过FCM算法得到的输入向量隶属于第k类的隶属度。h为可人工调整的尺度参数。

根据文献［8］描述，可令

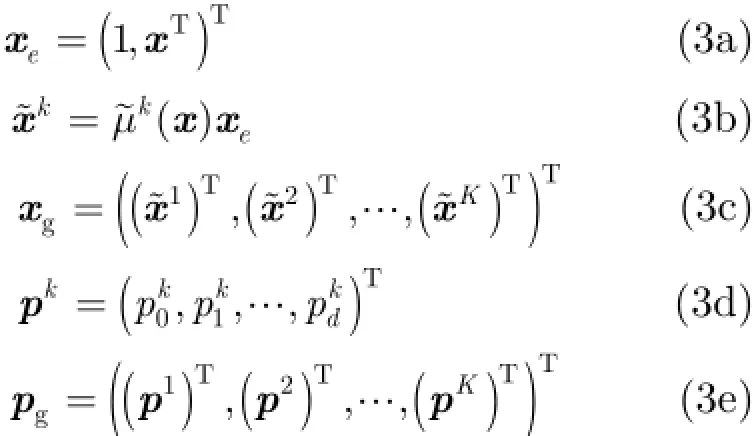
根据式（3a）～式（3e）可将式（2）改写为

通过上述描述，可知TSK型模糊系统的参数学习问题最终转化为了线性回归模型［8］。

2.2基于-e不敏感损失函数的L2型TSK型模糊系统

TSK模型基于-ε不敏感损失函数的目标函数式一般被定义为

通过引入松弛变量iξ+及iξ-，并根据二次规划理论，式（4）可转化为经典的二次规划问题，其具体形式为

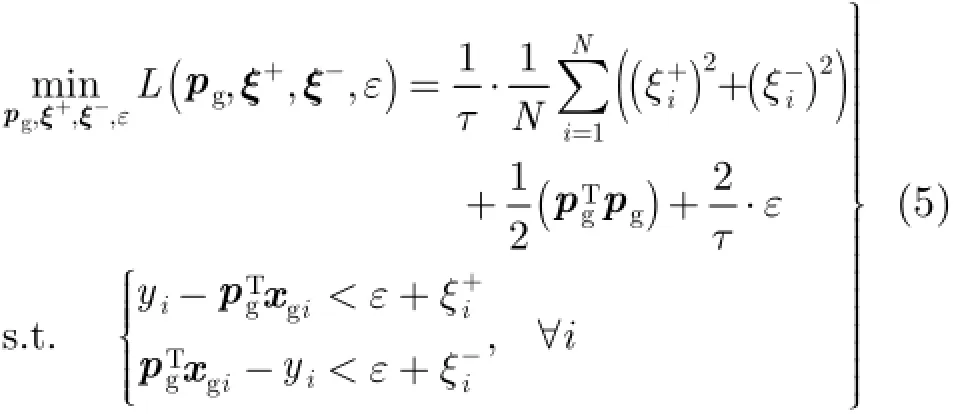
式（5）引入拉格朗日乘数项，可将式（4）化为式（6）的QP问题：

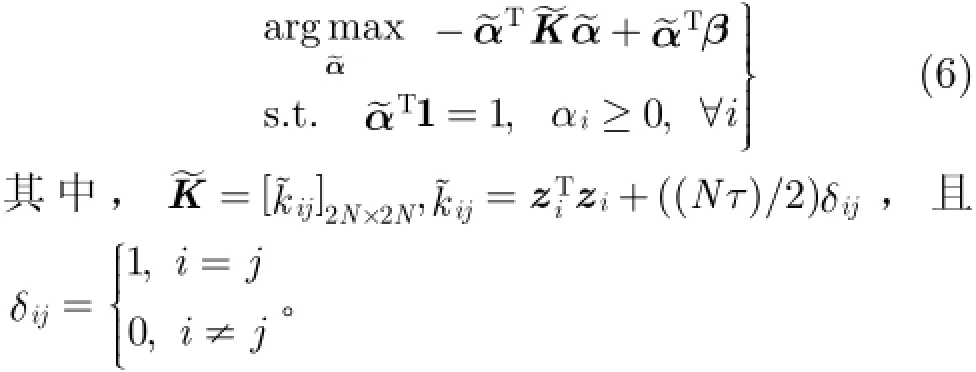
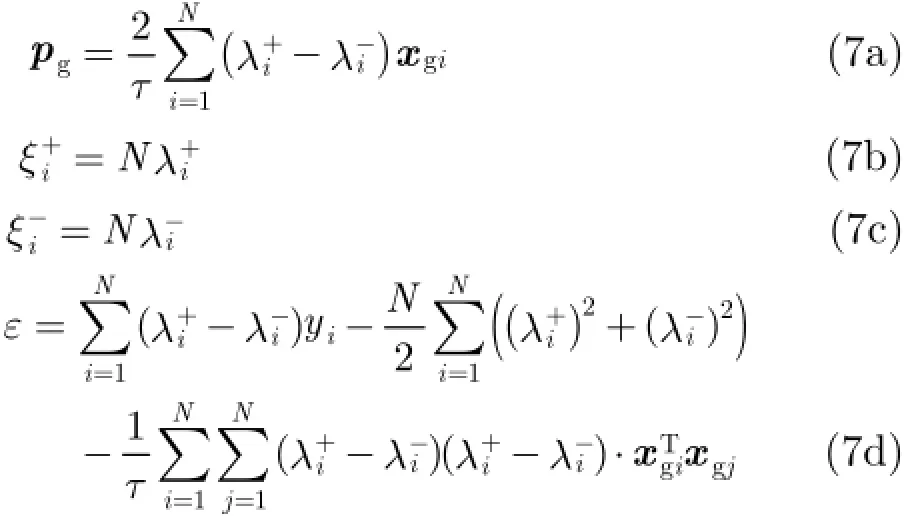
根据式（2d）及式（2e）所获之模糊系统前件参数并结合式（7a）所获得的模糊系统后件参数即可生成对应的TSK型模糊系统。

3　多视角TSK型模糊系统学习框架

根据第2节所提之经典TSK型模糊系统建模方法可知传统的系统建模策略均是针对单视角场景设计的，当该种经典建模方法在面对多视角建模场景时，较为可行的建模策略则是针对不同的视角利用该视角下的样本构建出与之对应的模糊系统，具体方法如图1所示。虽然上述策略为单视角建模方法在多视角场景下的应用提供了一种可行的方案，但是其针对每一视角较为独立的建模方式在一定程度上破坏了多视角数据集之间的关联关系，这通常会造成不同视角所获得之模糊系统泛化能力存在良莠不齐的现象。

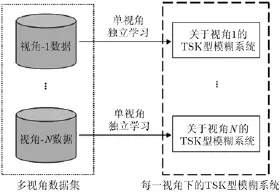
图1　面对多视角学习场景时传统的单视角TSK型模糊系统学习框架展示

为了使得传统的单视角TSK型模糊系统建模方法具备多视角学习的能力进而得到多视角TSK型模糊系统（MV-TSK-FS），本文给出了如图2所示的建模策略。观察图2可知，该建模方法较之传统单视角的建模方法而言，其不再将各视角下的数据样本孤立开来进行独立的模糊系统构建，而是通过多视角学习机制来训练不同视角下的模糊系统使得最终所获之各视角模糊系统泛化能力得到提升并性能趋于一致。具体的多视角TSK型模糊系统的模型构建方法将于第4节进行详细阐述。

4　多视角TSK型模糊系统建模方法

为改进单视角TSK型模糊系统，使其具备多视角学习能力，本节将在第2节所提及的TSK型模糊系统建模方式上应用多视角的学习原理构建多视角TSK型模糊系统（M u lti-V iew TSK type FuzzySystem，MV-TSK-FS）。为了公式简洁性，我们仅以2视角为例进行多视角模型构建。

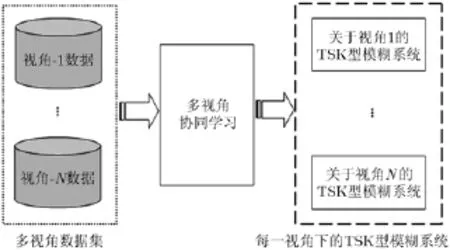
图2　面对多视角学习场景时新型的单视角TSK模糊系统学习框架展示

4.1具备多视角协同学习能力的目标函数构造

为了使得经典的L2型惩罚函数构造的TSK型模糊系统具备多视角学习的能力，本小节以双视角作为具体的研究场景探讨了多视角TSK型模糊系统的目标函数构造。在构建多视角TSK型模糊系统时，为了能够充分利用不同视角数据样本的特有特征（独立性信息）及各视角间样本内在的关联关系（关联性信息），本文给出了如下的具备多视角学习能力的目标函数式：

观察式（8）可发现该式由式（8a）～式（8c）3项构成，其中式（8a）及式（8b）分别为根据A和B视角样本特征构建的TSK型模糊系统，上述两项保证了所提方法能够充分利用不同视角下数据样本特征的差异性构建出属于该视角特征的专有模糊系统。但仅考虑视角间的样本特征差异性（独立性信息）对于整个多视角TSK型模糊系统的构建是不够的，为增强多视角学习的能力，所提方法进一步考虑了视角间的关联关系，即各视角决策（输出）的一致性。根据上述特性本文构造了具备协同学习能力的式（8c），该式可使得视角A与视角B进行协同学习，最终达到各视角所对应的模糊系统之输出趋于一致从而避免因视角特征的变化而造成各视角模糊系统的泛化性能的差异。需要说明的是正则化参数A0т>，B0т>，S0т>控制了回归模型的复杂度及误差程度，其数值可人工设定，亦可通过交叉验证策略［15］选择一个合适的值。

4.2 MV-TSK-FS参数学习规则

为求解式（8），根据拉格朗日优化理论，引入相关拉格朗日乘子，可将式（8）转换为式（9）：

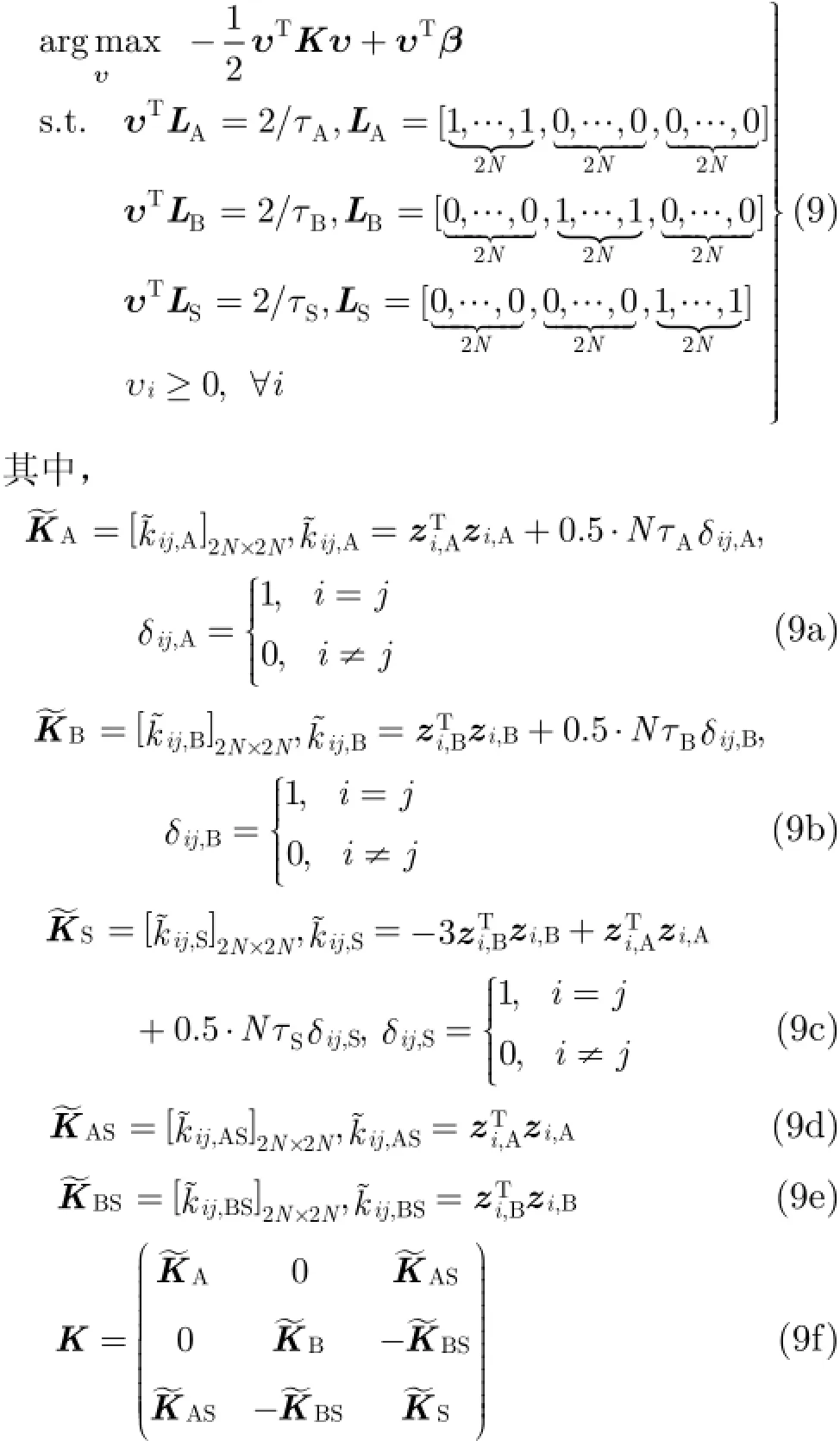
至此，式（8）被化为了如式（9）的经典QP问题，本文将采用文献［8］中的QP求解方法来求解式（9）。

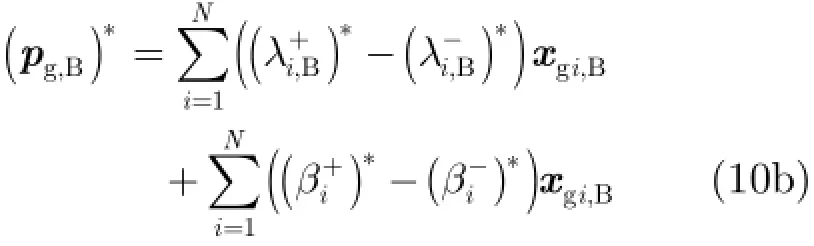
式（10a）为视角A对应的TSK型模糊系统的后件参数，而式（10b）则为视角B对应的TSK型模糊系统的后件参数。根据所获之后件参数结合式（2d）及式（2e）所得到的模糊系统前件参数即可生成一个多视角TSK型模糊系统。具体的多视角TSK型模糊系统（MV-TSK-FS）的学习算法如表1所示。

表1　 MV-TSK-FS算法

由算法1可知，MV-TSK-FS模糊系统的时间复杂度主要由两部分构成：前件参数的学习（对应步骤2）和后件参数的学习（对应步骤3与步骤4）。在多视角学习中，MV-TSK-FS的每个视角对应的模糊系统的前件参数由FCM聚类算法获得，其时间复杂度是O（M TNK+M TK），其中M为视角的个数，T为算法迭代次数，N为样本数，K为模糊系统规则条数。MV-TSK-FS的每个视角的后件参数的学习关键在二次规划求极值问题上，时间复杂度为，通过使用SMO等分解方法处理二次规划问题，其时间复杂度可降为O（N2），因此，多视角学习中，MV-TSK-FS的后件参数的学习的时间复杂度为之间。此外，因本文采用的对比方法，即经典TSK模糊系统建模方法［8］为一种快速建模方法，其时间复杂度仅为O（TNK+TK）+ O（N2），因此所提出的多视角MV-TSK-FS模糊系统在时间性能上要劣于单视角TSK模糊系统建模方法。究其主要原因在于，MV-TSK-FS模糊系统建模策略融入了多视角协同学习策略，而单视角TSK模糊系统并不具备多视角学习能力，因此MVTSK-FS模糊系统更为耗时，但其泛化性能较之经典单视角TSK模糊系统有着较大的提升。

5　实验研究

5.1实验设置

为对本文所提之多视角TSK型模糊系统（MVTSK-FS）的性能进行验证与评估，本节将分别采用人工合成的多视角数据集以及真实的谷氨酸发酵多视角数据集进行实验研究。其中合成数据以及谷氨酸真实数据将分别于5.2.1节和5.2.2节中给出具体描述。此外，实验中所涉及的一些符号定义如下：D 1和D2分别表示为多视角场景下视角1和视角2的训练数据集，D 1_test和D 2_test则为测试数据集；［D 1；D 2］表示为视角1及视角2训练数据集以特征扩展的方式合并得到的单视角训练数据集，［D 1；D 2］_test为测试数据集；TSK-FS（View-D 1），TSKFS（View-D 2）及TSK-FS（View-［D 1；D 2］）分别为单视角TSK-FS基于D1，D 2及［D 1；D 2］数据集所构之模糊系统；MV-TSK-FS（V iew-D 1）和MV-TSK-FS（View-D 2）则为本文所提之多视角MV-TSK-FS建模方法基于D1和D 2所构之模糊系统。

为了对本文的实验结果给出合理的评价，采用式（11）作为性能评价指标［8］。

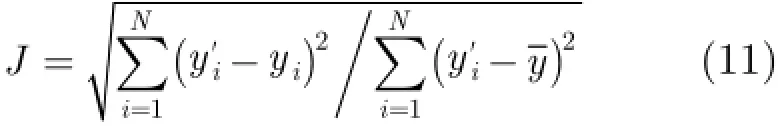
其中，N为测试样本集尺寸；yi为第n个测试样本的真实输出；表示第n个测试样本对应的模糊系统输出；J 越小则表示泛化能力越好。

在实验中，所涉人工设定参数均采用如表2所述之优化策略。实验环境：实验硬件平台为Intel Pentium×2 CPU，其主频为1.6 GHz，内存为1 GB。编程环境为MATLAB 7.0。

5.2本文方法与经典L2-TSK-FS性能比较

5.2.1合成数据集为了能够体现多视角数据集各视角特征构成的独立性以及视角之间的关联关系，本文根据上述的多视角数据的特点分别选用sin（x1）函数以及函数来表征两个独立的视角，并利用sin（x）函数与cos（π/2-x）函数具备相同的函数值的特点来形成两视角之间的关联关系（令x1=x而这样构成的多视角样本集在各视角下，虽然输入特征不同（视角间的独立性），但最终各视角的输出却是一致的（视角间的关联性）。具体的函数定义及相关采样区间的描述可见表3所述。具体人工数据实验结果如表4和图3所示。

根据表4和图3所示的合成数据集上的实验结果，我们归纳出如下观察结果：

（1）从表4以及图3（a）和图3（b）的实验结果看，无论是V iew（D 1）视角还是V iew（D2）视角的结果，均说明了由本文方法所构之模糊系统性能要明显优于经典单视角TSK型模糊系统的性能。这说明本文方法因具备多视角学习的能力较之经典的单视角方法能够更加有效地利用多视角数据集中各视角较为独立的特征空间信息以及视角与视角之间的关联关系，从而使得本文方法能够更好地提升在各视角上所建之模糊系统的泛化能力。

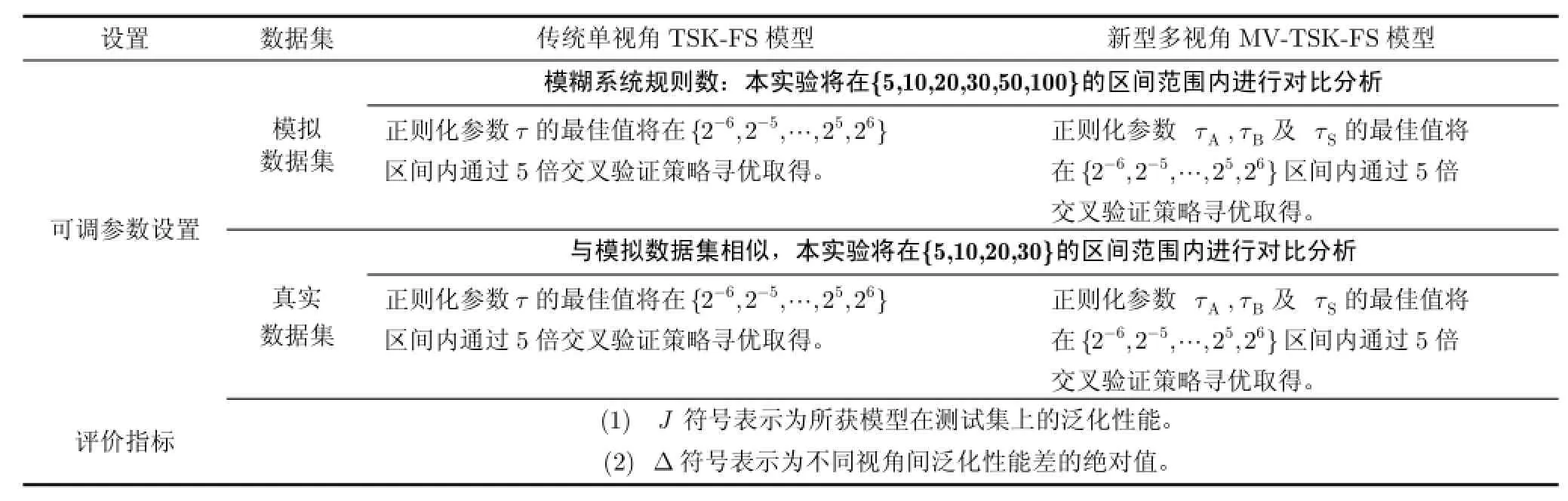
表2　相关实验设置

表3　相关数据源生成函数定义

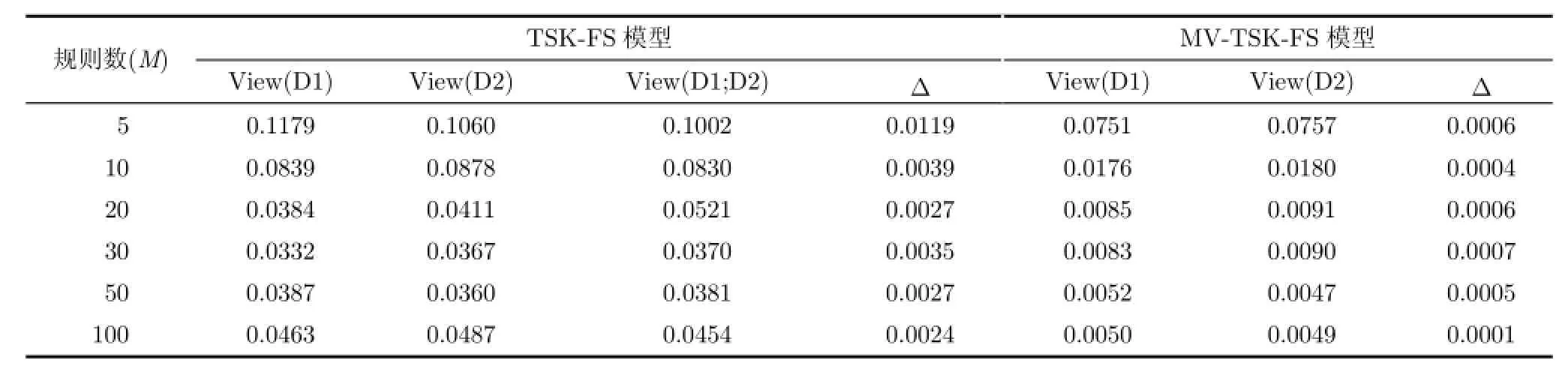
表4　多视角MV-TSK-FS建模方法及传统TSK-FS建模方法在模拟数据集上的泛化性能比较

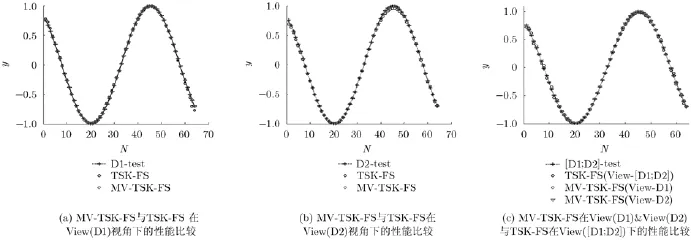
图3　 MV-TSK-FS建模方法及传统的TSK-FS建模方法在模糊规则数30K=的情况下各自的性能比较

（2）从图3（c）的实验结果看，各视角虽然存在一定的关联关系如一致性的输出成分，但视角间的差异性亦是明显的，如输入成分（输入特征空间）。这种差异性导致经典单视角TSK型模糊系统在使用人为构造的单视角样本［D 1；D 2］进行训练后所构建模型的泛化性能明显劣于任意视角下基于本文方法构建的模型的性能。根据上述的结果说明了仅考虑视角间的关联性而忽视了视角间独立性（存在差异的特征空间）也是不可行的。

（3）进一步观察图3（a）-图3（c）以及表4的TSKFS性能的第4列与MV-TSK-FS性能的第3列，可以发现经典单视角方法得到的各视角模糊系统的性能指标差明显大于本文方法得到的各视角模糊系统的性能指标差，这说明单视角方法得到的模糊系统性能并不稳定，各视角模糊系统的性能存在良莠不齐的现象，而本文方法由于采用了多视角协同学习的策略，使得其最终生成的各视角方法系统的性能在提升的同时还具备相互接近的稳定状态，这一点从图3（c）中的“◇”线和“▽”线的重合程度可以得到进一步的证实。

5.2.2真实数据集本小节利用具备多视角特征的发酵过程数据集［8］来进行建模仿真实验以进一步验证本文方法与经典TSK型模糊系统的性能比较，通过对采集到的工厂发酵数据进行筛选和分析后，本文选择其中具有代表性并且覆盖较为广泛的21批共294组数据样本作为研究对象，该数据集包含两个视角样本分别为：（1）根据搅拌速度为主特征的视角样本D 1；（2）根据通风指数为主特征的视角样本D2。最终实验结果如表5所示。

从表5的实验结果可知，其实验结果与上节中在合成数据的观察结果基本是一致的。具备多视角学习能力的TSK型模糊系统在模型训练时，其能够通过充分利用多视角数据集的独立性成分和关联性成分训练得到有关各视角的模糊系统。对于这些得到的各视角模糊系统，我们无论是从独立的单一视角看，还是从不同视角之间系统的泛化性能关联关系角度分析，所得结论均显示出了本文方法比传统单视角方法在处理多视角问题具有更好的泛化性能，且各视角下的系统性能更为稳定。因此利用本文方法构建的模糊系统可以更加准确地监控发酵过程，并进行相应的预测。

6　结束语

本文针对传统的模糊系统建模方法在处理多视角场景仅利用了视角间的独立性信息而忽视了视角间样本的关联性信息，从而导致各视角所构之模糊系统泛化能力差且性能存在良莠不齐的现象，提出了多视角协同学习的思想并将该方法融入具体的TSK型模糊系统中，得到了具备多视角学习能力的多视角TSK型模糊系统。该方法能够有效且充分地利用多视角数据集中的独立性成分和视角之间的关联性成分，进而提高各视角下模糊系统的泛化性能并通过协同学习机制进一步稳定各视角模糊系统的性能。通过在模拟数据集以及真实的发酵过程数据集上的仿真实验结果，显示本文方法比传统的单视角建模方法具备更好的适应性。但由于多视角算法的复杂性，在本文的研究工作中仅给出了双视角下的MV-TSK-FS的具体建模方法，在今后的工作中将致力于研究出一种推导及计算更为简洁且更适于推广的多视角TSK型模糊系统的建模方法，同时也将考虑其他经典模糊系统模型的多视角化构建问题。

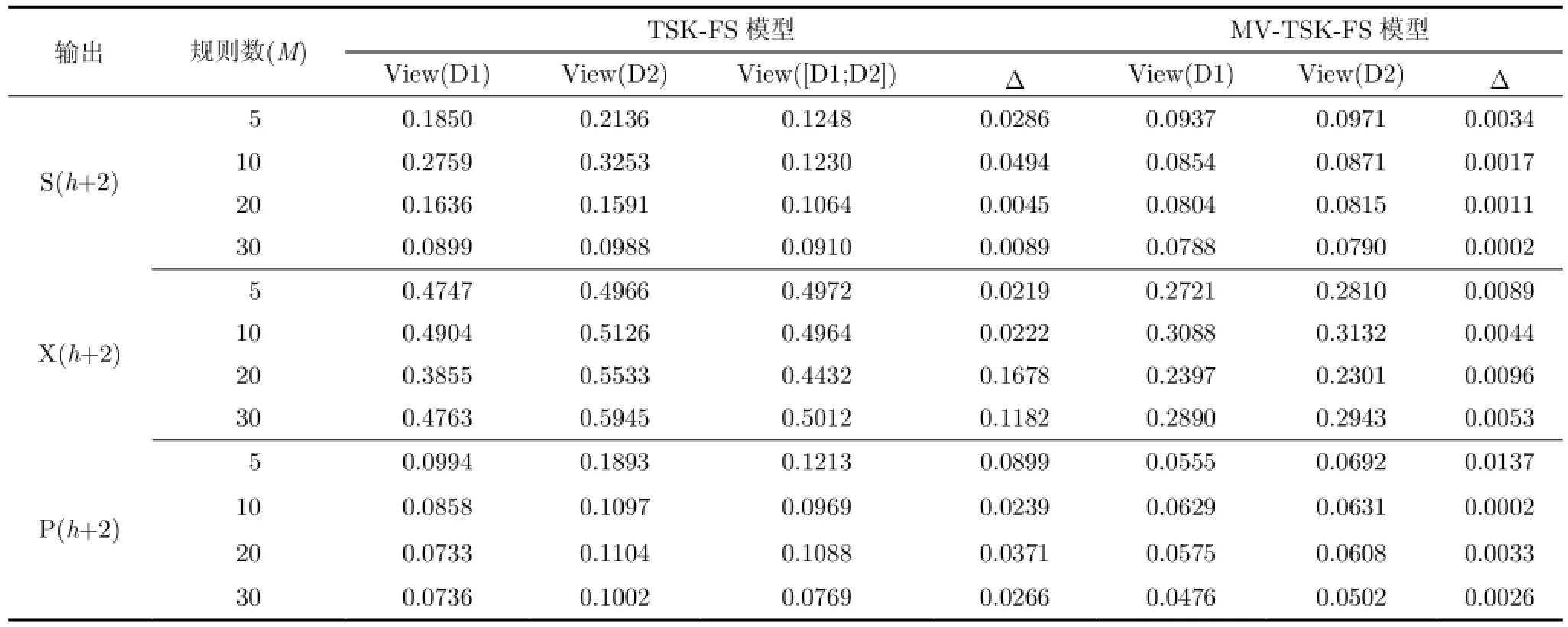
表5　多视角MV-TSK-FS建模方法及传统TSK-FS建模方法在真实发酵数据集上的泛化性能比较

［1］LI Guangxia，CHANG Kuiyu，and HOI S C H.Multiview sem i-supervised learning w ith consensus［J］.IEEE Transactions on Know ledge and Data Engineering，2012，24（11）:2040-2051.doi:10.1109/TKDE.2011.160.

［2］HONG Chaoqun，YU Jun，YOU Jane，et al.Mu lti-view ensemble manifold regularization for 3D ob ject recognition［J］.Information Sciences，2015，320:395-405.doi:10.1016/ j.ins.2015.03.032.

［3］ZHANG Shun li，YU X in，SU IYao，et al.Ob ject trackingw ith multi-view support vector m ach ines［J］.IEEE Transactions on Multim edia，2015，17（3）:265-278.doi:10.1109/TMM. 2015.2390044.

［4］蒋亦樟，邓赵红，王骏，等.熵加权多视角协同划分模糊聚类算法［J］.软件学报，2014，25（10）:2293-2311.doi:10.13328/j. cnki.jos.004510.

JIANG Yizhang，DENG Zhaohong，WANG Jun，et al. Collaborative partition multi-view fuzzy clustering algorithm using entropy weighting［J］.JournalofSoftware，2014，25（10）: 2293-2311.doi:10.13328/j.cnki.jos.004510.

［5］TZORTZIS G F and LIKAS A C.M ultip le view clustering using a weigh ted com bination of exemp lar-based m ixtu re m odels［J］.IEEE Transactions on Neural Network，2010，21（12）:1925-1938.doi:10.1109/TNN.2010.2081999.

［6］JIANG Yizhang，CHUNG Fulai，WANG Shitong，et al. Collaborative fuzzy clustering from mu ltiple weighted view s［J］.IEEE Transactions on Cybernetics，2015，45（4）: 688-701.doi:10.1109/TCYB.2014.2334595.

［7］MERUGU S，ROSSET S，and PERLICH C.A new m ultiview regression app roach w ith an app lication to customer wallet estimation［C］.Proceedings of 12th ACM SIGKDD International Con ference on Know ledge Discovery and Data M ining，Philadelphia，USA，2006:656-661.

［8］DENG Zhaohong，JIANG Y izhang，CHOI Kupsze，et al. Know ledge-leverage-based TSK fuzzy system m odeling［J］. IEEE Transactions on Neural Networks and Learning System s，2013，24（8）:1200-1212.doi:10.1109/FUZZ-IEEE. 2014.6891544.

［9］ÅSTR M K J and MCAVOY T J.Intelligent control［J］. Journal of Process Con trol，1992，2（3）:115-127.

［10］邓赵红，张江滨，蒋亦樟，等.基于模糊子空间聚类的〇阶L2型TSK模糊系统［J］.电子与信息学报，2015，37（9）:2082-2088. doi:10.11999/JEIT 150074.

DENG Zhaohong，ZHANG Jiangbin，JIANG Yizhang，et al. Fuzzy subspace clustering based zero-order L2-norm TSK fuzzy system［J］.Journal of Electronics&Information Technology，2015，37（9）:2082-2088.

［11］TAKAGIT and SUGENO M.Fuzzy identification of system s and its app lication to m odeling and control［J］.IEEE Transactions on System s，M an，and Cybernetics，1985，15（1）: 116-132.doi:10.1109/TSMC.1985.6313399.

［12］MAMDANIE H.Application of fuzzy logic to app roximate reasoning using linguistic synthesis［J］.IEEE Transactions on Computers，1977，26（12）:1182-1191.doi:10.1109/TC.1977. 1674779.

［13］AZEEM M F，HANM ANDLU M，and AHMAD N. Generalization of adaptive neural-fuzzy in ference system s［J］. IEEE Transactions on Neural Networks，2000，11（6）: 1332-1346.doi:10.1109/72.883438.

［14］JIANG Y izhang，CHUNG Fulai，and WANG Shitong. Enhanced fuzzy partitions vs data randomness in FCM［J］. Journal of Intelligent and Fuzzy System s，2014，27（4）: 1639-1648.doi:10.3233/IFS-141130.

［15］ITO K and NAKANO R.Op timizing support vector regression hyperparameters based on cross-validation［C］. Proceedings of the International Joint Conference on Neural Networks，Jantzen Beach，Portland，Oregon，2003: 2077-2082.

程旸：男，1991年生，博士生，研究方向为计算智能和模糊计算.

顾晓清：女，1981年生，讲师，博士生，研究方向为计算智能和模糊计算.

蒋亦樟：男，1988年生，讲师，博士，研究方向为计算智能和模糊计算.

杭文龙：男，1988年生，博士生，研究方向为人工智能和模式识别.

钱鹏江：男，1979年生，副教授，硕士生导师，研究方向为人工智能和模式识别.

王士同：男，1964年生，教授，博士生导师，研究方向为人工智能和模式识别.

Multi-view TSK Fuzzy System via Collaborative Learning

CHENG Yang GU Xiaoqing JIANG Y izhang HANG Wen long QIAN Pengjiang WANG Shitong
（School ofDigitalMedia，Jiangnan University，W uxi 214122，China）

Conventional fuzzy system modelingmethods essentially belong to the single-view learningmodality.In multi-view-oriented data scenarios，they can on ly cope w ith each view separately，which is p rone to incu rring their unsatisfactory generalization perform ance.In response to such p rob lem，the fuzzy system m odeling m ethod w ith the ability ofmu lti-view learning is pursued.To this end，based on the classic L2 norm Takagi-Sugeno-Kang（TSK）fuzzy system，by means of the collaborative learning items qualified formulti-view learning，the core Multi-View TSK Fuzzy System（MV-TSK-FS）modelingmethod is presented.MV-TSK-FS can not on ly effectively utilize the independent com ponents composed of the characteristics affiliated to each view，but also take full advantage of the potential in formation occurred by the interrelated effects among views，which eventually facilitates its relatively strong generalization ability.The experimental results performed on both synthetic and real-life datasets indicate that，compared w ith some traditional single-view methods，this propounded multi-view fuzzy modeling system owns p referable app licability aswell as generalization.

Multi-view learning；Collaborative learning；Fuzzy modeling；Takagi-Sugeno-Kang（TSK）type fuzzy system

1　引言

经典的哲学理论告诉我们多视角学习方法较之传统的单视角学习策略，在看待问题方面更为全面与客观，并且大量的实际应用，如多视角文本分类及多视角行为识别等均说明了该方法的有效性。近年来多视角学习在机器学习领域得到了迅猛发展，具体工作可归纳为：（1）分类领域的多视角学习［13］-；（2）无监督学习，特别是聚类领域的多视角学习［46］-；（3）回归领域的多视角学习［7］。其中，在分类和聚类领域内的多视角学习成果已较为丰富，但相对而言，针对回归领域的多视角学习理论研究则较少。然而，在回归领域多视角学习方式同样具有很好的应用前景及研究价值。以食品的发酵过程为例［8］，在对同一食品的发酵过程进行检测时，我们可从不同的角度，如风速或搅拌速度，来记录食品的发酵指标参数值（即输出值）。因角度不同从而导致输入空间构成不同（独立性），但又因观测对象相同，这使得各视角的最终输出是一致的（关联性），根据上述性质即可得到一个多视角样本集。同时，由于发酵过程是一个随着时间变化的连续性函数，因此对其的预测可视为回归问题。上述需求，促使我们应当在回归领域开展多视角学习研究。

s:The National Natural Science Foundation of China（61300151），The Natural Science Foundation of Jiangsu Province（BK 20130155），The R&D Frontier G rant of Jiangsu Province（BY 2013015-02），The Fundamental Research Funds for the Central Universities（JUSRP51614A）

TP391

A

1009-5896（2016）08-2054-08

10.11999/JEIT 151209

2015-10-29；改回日期：2016-03-15；网络出版：2016-05-05

蒋亦樟jyz0512@163.com

国家自然科学基金（61300151），江苏省自然科学基金（BK 20130155），江苏省产学研前瞻性联合研究项目（BY 2013015-02），中央高校基本科研业务费专项资金资助重点项目（JUSRP 51614A）