采用多级残差滤波的非局部均值图像去噪方法

孙伟峰　戴永寿（中国石油大学（华东）信息与控制工程学院青岛266580）



采用多级残差滤波的非局部均值图像去噪方法

孙伟峰*戴永寿
（中国石油大学（华东）信息与控制工程学院青岛266580）

为充分利用残差中的图像信息以提升非局部均值算法的去噪性能，该文提出一种多级残差图像滤波新方法。首先对含噪图像进行非局部均值滤波得到初始的去噪图像和权值分布矩阵，然后对残差图像进行固定权值非局部均值滤波来提取图像结构信息，将提取的信息经高斯平滑抑噪后作为补偿图像，与去噪图像相加得到增强的恢复图像。针对上述方法提出一种多级滤波的实现方案，从理论上推导证明了该方法的原理及可行性，并提出一种无需参考图像的迭代停止准则来自适应地优选滤波级数。实验结果表明，提出的迭代停止准则能够达到与峰值信噪比一致的优选结果；与经典的非局部均值算法相比，在计算效率相当的情况下，所提方法能够显著地提升其去噪性能，峰值信噪比平均可以提高1.2 dB，且具有更好的细节保持能力。

图像去噪；非局部均值；残差滤波；停止准则

1　引言

数字图像在获取、传输等过程中不可避免地会受到噪声的影响，噪声的引入会降低图像质量，进而影响图像分割、配准、识别等图像处理任务的性能。因此，作为一种重要的预处理手段，图像去噪一直是图像处理领域中一个基础且重要的研究课题，其难点在于如何在噪声去除与图像特征保留之间达到平衡。

非局部均值（Non-Local Means，NLM）算法［1］是空域滤波方法的新发展，被广泛应用于图像与视频降噪［24］-。以此方法为基础，发展了一系列基于图像分块（patch-based）表示的图像去噪方法［510］-，取得了先进的去噪结果。非局部均值算法利用图像分块间的相似性质去除噪声，具有良好的边缘保持能力；然而，由于算法参数选择不合适、相似性权值计算不准确等不足，在滤除噪声的同时，也会丢失一些图像细节成分，这部分信息将存在于残差图像中，目前，大多数图像去噪方法都致力于设计算法使得去噪图像更逼近原始图像，而很少考虑如何令残差图像逼近纯噪声，没有很好地利用残差图像提供的信息。

近年来，越来越多的学者认识到残差图像中蕴含信息的重要性，提出了许多残差图像处理方法来提高去噪算法的性能。例如，文献［11］提出采用自适应维纳滤波从残差图像中提取图像的结构信息。文献［12］设计了一种多边滤波器对残差图像进行滤波；文献［13］将该方法取代BM 3D算法中的维纳滤波环节，更好地保持了图像的结构特征。文献［14］利用残差图像的信息修正NLM算法中的权值表达，提高了权值计算的准确性。文献［15］采用小波阈值的方法对残差图像进行处理，提升了NLM算法的去噪性能。文献［16］提出一种残差图像后处理方式来增强K-SVD算法的去噪能力，并发展了一种通用的增强图像去噪算法性能的递归算法［17］。可见，残差中图像信息的利用为提升去噪算法的性能提供了一种新的途径。

为进一步提升NLM算法的去噪性能，本文提出一种多级残差图像滤波新方法。该方法以固定权值非局部均值滤波与高斯滤波作为基本的处理模块，通过对残差中图像信息的逐级提取与补偿，提高去噪图像质量；基于残差图像提出了一种无需参考图像的图像质量评价准则进行最优滤波级数选择，兼顾了噪声去除与图像细节保留。从理论推导分析与实验结果验证两个方面证明了提出方法的有效性。

2　非局部均值去噪算法与残差图像

2.1非局部均值去噪算法

给定一幅含噪图像y，对于其中的任何一个像素i，NLM算法利用搜索邻域内所有像素值的加权平均作为该点的估计值（）x iˆ，即：

其中，Ω表示以像素i为中心的搜索邻域；（，）i jω为像素i与j之间的相似性权值，定义为

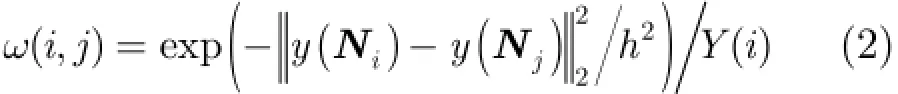
式（2）中，iN表示以像素i为中心的固定大小的图像块，称为相似邻域，为归一化常数，h为滤波参数。文中将由所有（，）i jω构成的矩阵W称为NLM算法的权值分布矩阵，将采用已知权值分布矩阵的NLM算法称为固定权值非局部均值滤波方法。

2.2残差图像

残差图像也被称为“方法噪声”［1］，定义为含噪图像与去噪图像之间的差值。理想情况下，去噪过程中应该仅有噪声被滤除，因而对于一个好的去噪方法，其残差图像应该类似白噪声。而实际上，即使对于目前最先进的去噪方法，其残差图像中仍然包含图像细节信息［15］。

在Lena图像中加入标准差为25的高斯白噪声，利用非局部均值算法进行去噪，得到的去噪图像及相应的残差图像如图1所示。可见，残差图像中包含明显的图像结构信息，若能够有效提取这些信息并将其反馈至去噪图像中，必然能够增强去噪图像中的细节特征。基于这个思路，为了充分提取残差中的图像结构信息，本文提出了一种多级残差图像滤波方法，用以增强NLM算法的去噪性能。

3　采用多级残差滤波的非局部均值图像去噪方法

非局部均值算法的权值分布矩阵反映了像素间的结构相似性，观察图1（b）可见，残差图像与含噪图像中包含相似的图像结构，可以采用相同的权值分布矩阵对残差图像进行非局部均值滤波来提取图像结构信息。由于滤波过程在强噪声背景下进行，提取的图像信息中必然包含噪声成分，为了削弱噪声的影响，在反馈至去噪图像之前，本文采用高斯滤波进行降噪处理。这样，就构成了本文提出的残差图像滤波方法的两个核心模块：固定权值非局部均值滤波与高斯平滑。

图1　去噪图像与残差图像示例

为了更加充分地提取残差中的图像信息，对上述方法提出一种多级滤波的实现方案，使图像信息提取与补偿环节交织进行；此外，利用去噪图像、残差图像与含噪图像之间的相关性提出了一种迭代停止准则，能够对滤波级数进行自适应优选。由此，发展了一种新的多级残差图像滤波方法。

3.1算法原理

W为N N×的正定矩阵，对其进行特征值分解得=W V d。其中，其对角线上包含由小到大排列的特征值为正交矩阵，其每一列为对应特征值λ1，λ2，…，λN的特征向量。利用矩阵V的列向量构成的空间对图像x进行分解得=x V b。

基于上述表示，对含噪图像进行非局部均值滤波得到初始去噪图像对于本文提出的基于固定权值非局部均值滤波的多级残差滤波方法，第k次迭代得到的去噪图像kxˆ可以表示为

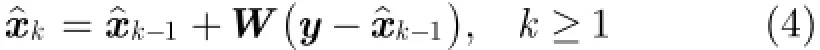
将式（4）展开表示成含噪图像y的函数的形式为

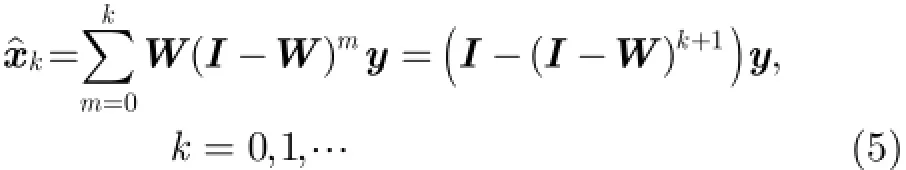
式（5）中，I表示N N×的单位矩阵。为了分析提出方法的有效性，对迭代过程中所得降噪图像的均方误差值随迭代次数的变化规律进行讨论。第k次迭代时，所得估计图像的偏差为

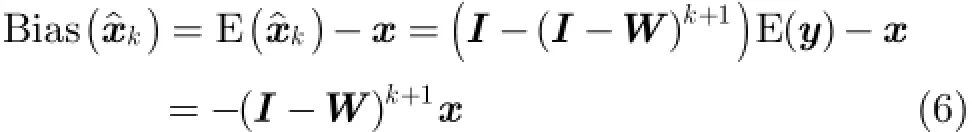
其中，E（）⋅表示求数学期望。偏差模值的平方表示为

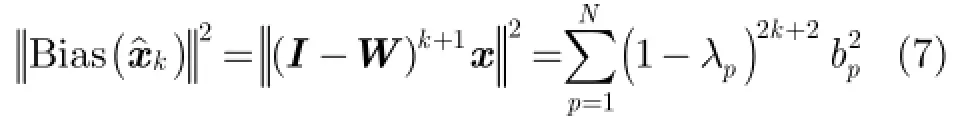
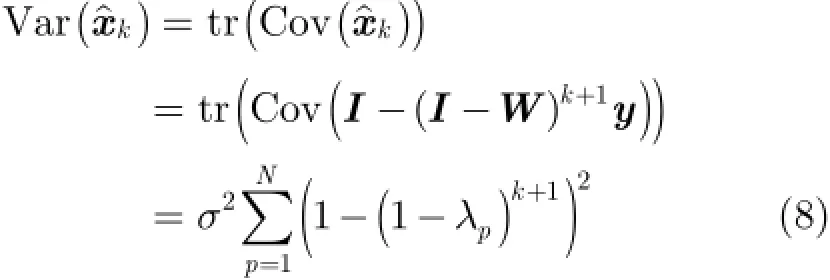
其中，tr（）⋅与Cov（）⋅分别表示求矩阵的迹与协方差。由此，第k次迭代后所得去噪图像的均方误差可以表示为

由式（7）～式（9）可知，随着迭代次数k的增加，所得估计图像的偏差将逐渐减小，而方差将逐渐增大，当k→∞时，所得去噪图像的方差将趋于，即将收敛到含噪图像y。

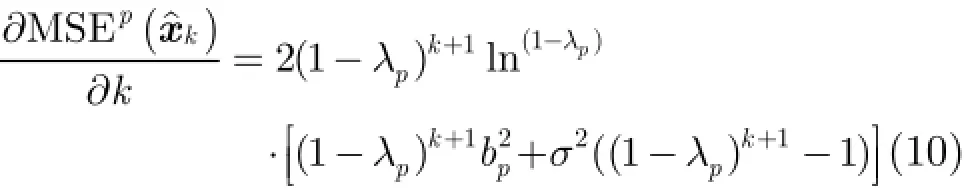
令式（10）等于零，得到对第p个像素点估计时的最优迭代次数

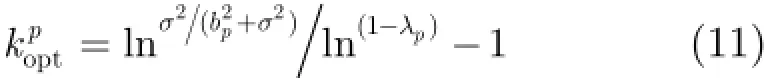
上述分析证明，在一定的迭代次数范围内，对残差图像进行多级固定权值非局部均值滤波，利用提取的信息对去噪图像进行补偿，能够在均方误差意义上提高去噪图像的质量，从而证明了本文方法在原理上的可行性。然而，在实际的去噪过程中，很难对每一个像素点处的信号能量进行准确估计，因而无法通过直接计算得到。注意到，尽管对于不同的像素点，也不尽相同，很难找到一个统一的迭代次数，使得对每个像素的估计都能达到均方误差意义上的最优，但是，必然存在一个迭代次数，能够从整体上优化去噪效果，本文在3.3节提出一种停止准则来确定该“最优”的迭代次数。

3.2算法描述

采用多级残差滤波的非局部均值图像去噪算法的流程图如图2所示。

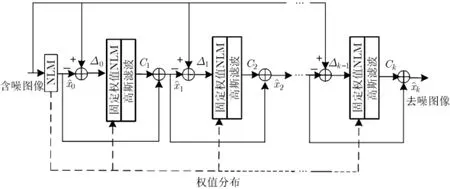
图2　算法流程图

具体步骤如下：

（1）令k=0，对含噪图像y利用NLM算法进行去噪，得到初始去噪图像及权值分布矩阵W；

（3）令k=k+1，采用权值分布矩阵W对残差图像进行固定权值NLM滤波，再经过高斯滤波抑制噪声后，得到补偿图像Ck；

（5）重复步骤（2）～步骤（4），直至达到最优滤波级数k*；

（6）将得到的ˆxk*作为最终的去噪结果。

3.3停止准则

多级残差滤波过程中，每一级滤波得到的去噪图像与残差图像都在变化，算法将最终收敛到含噪图像。因此，停止准则的选择尤为重要，决定着算法的性能与计算复杂度。本文基于去噪图像、残差图像与含噪图像之间的相关性［18］，提出了一种无参考的图像质量评价方法，用来选择最优的滤波级数。根据皮尔逊相关系数，按式（12）计算两幅大小为

基于上述考虑，本文提出采用内积的方式实现两者之间的线性相关，定义为

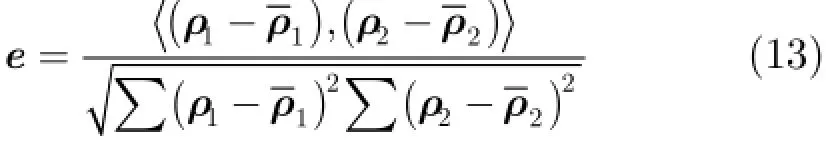
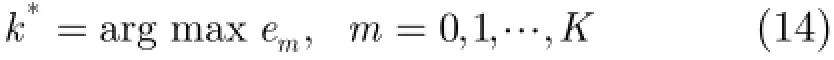
其中，me表示e的第m个元素。

4　实验结果与分析

利用大小为512×512的Lena，Barbara，Boat以及256×256的House，Peppers5幅标准测试图像及一幅实际的含噪图像开展去噪实验，对本文方法的有效性进行验证。

4.1停止准则实验验证

以峰值信噪比（Peak Signal to Noise Ratio，PSNR）作为评价标准，利用提出的去噪方法进行固定迭代次数去噪实验，迭代次数取10，对3.3节中提出的停止准则进行验证、评价。

首先，在Lena图像中加入标准差为10～50的高斯白噪声，采用PSNR准则与本文提出的e值准则判定最优的迭代次数，结果如图3所示。

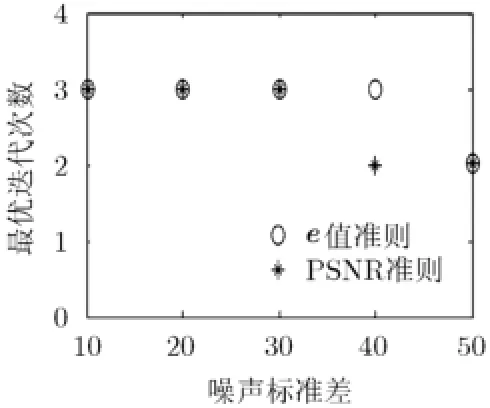
图3　最优迭代次数比较

由图3中的结果可见，由PSNR准则与e值准则确定的最优迭代次数具有高度的一致性，一般经过2～3次迭代即可取得最优的结果。噪声标准差为40时，由PSNR准则与e值准则确定的最优迭代次数分别为2和3，此时，利用PSNR准则得到的峰值信噪比仅比e值准则得到的高0.05 dB。

然后，对PSNR准则与e值准则在不同迭代次数下的变化规律进行比较。在Lena图像中加入标准差为20的高斯白噪声，不同迭代次数下，去噪图像与含噪图像、残差图像与含噪图像之间的相关系数曲线如图4（a）所示，PSNR与e值曲线如图4（b）所示，其中，横坐标表示迭代次数，0值对应初始NLM算法的去噪结果。可见，随着迭代次数的增加，去噪图像与含噪图像之间的相关系数首先逐渐增大，当迭代次数为7时增至最大；而残差图像中由于不断有图像信息被抽取出来，其与含噪图像之间的相关性逐渐减弱。e值曲线与PSNR曲线呈现出一致的变化规律，当迭代次数为3时，两者都达到最大值。

迭代次数取0～3时所得的去噪图像及对应残差图像的局部图如图5所示，可以看出，在达到最优的迭代次数之前，随着迭代的进行，所得去噪图像中的细节信息逐渐丰富，如帽子上的纹理部分，同时，对应残差图像中包含的图像结构信息逐渐减弱。

4.2峰值信噪比与结构相似性比较实验

在5幅测试图像中分别加入标准差为10～50的高斯白噪声，利用原始NLM［1］，NLFMT［15］，PPB 25it［6］和本文方法开展去噪实验。所有方法中，相似性邻域与搜索邻域的大小分别取7×7与21×21［1］，NLM算法的滤波参数h =1.0×7×7×σ2；高斯滤波器大小为3×3，标准差为1.0。采用峰值信噪比与结构相似指数准则（Structural Sim ilarity Index Metric，SSIM）［19］对不同方法的去噪结果进行定量比较。所得PSNR与SSIM的结果分别列于表1～表2中，每个单元格内，左上、右上、左下、右下4个数据分别代表原始NLM，NLFMT，PPB 25it以及本文方法的去噪结果，最好的结果用加粗字体表示。

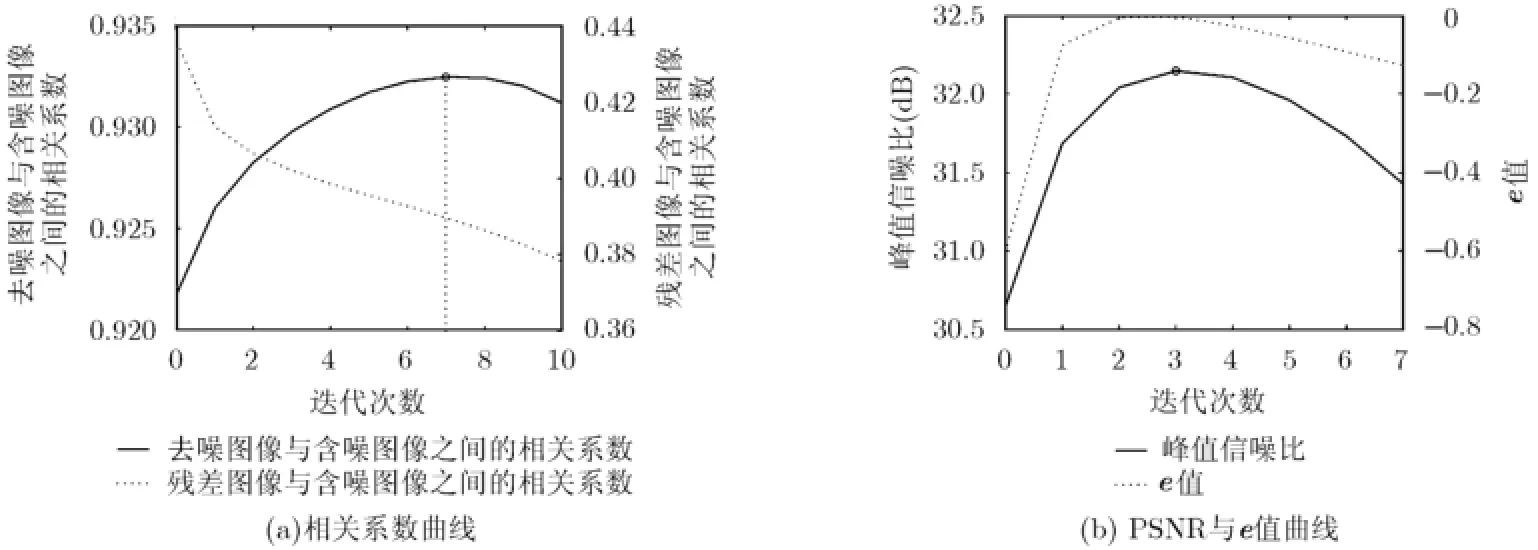
图4　不同迭代次数下相关系数、e值与PSNR曲线

图5　不同迭代次数下的去噪图像与残差图像

表1　峰值信噪比比较结果

由表1中的数据可以看出，对于5幅测试图像，在噪声标准差小于30时，本文方法能够得到最高的PSNR值；在噪声水平较高时，由于原始NLM算法的权值分布矩阵计算不准确，影响了本文方法的去噪效果，但仍然能够取得与PPB 25it接近的峰值信噪比；与原始NLM算法相比，本文方法在峰值信噪比方面平均可以获得1.2 dB的增益，最多可以提高1.54 dB。

由表2中的结果可以看出，本文方法在较低的噪声水平下能够获得最高的结构相似性，说明本文方法具有良好的结构保持能力。在噪声水平较高时，本文方法会在某些去噪图像中引入伪结构信息，使得结构相似性有所降低。

实验发现，本文方法一般需要迭代2～3次即可取得最优的去噪结果。与取得先进去噪效果的PPB 25it方法相比，本文方法在噪声水平较低时，能够得到优于PPB 25it方法的峰值信噪比与结构相似指数；在较高的噪声水平下，本文方法可以取得与PPB 25it相近的去噪效果，但本文方法的计算复杂度远远低于该方法。4种方法的平均运行时间对比见表3所示，所有方法都是在matlab R2013a平台上运行，计算机配置为3.20 GHz Intel Core i5 CPU，4.0 GB内存。由于非局部均值算法的计算量主要集中在相似性权值的计算上，而本文方法采用固定权值非局部均值滤波，且只需进行2～3次迭代，计算效率仍然较高。

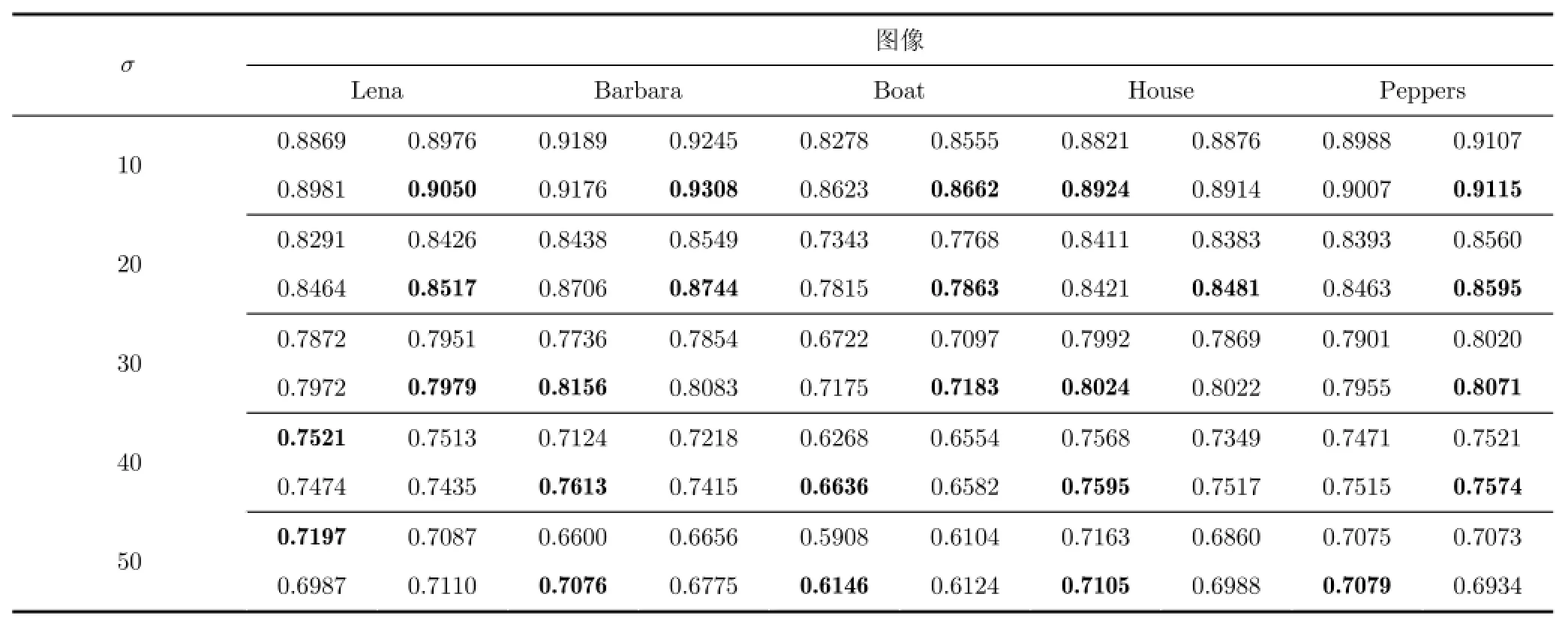
表2　结构相似指数比较结果

表3　 4种算法平均运行时间对比（s）

4.3方法噪声比较实验

以Lena图像为例，对其加入标准差为20的高斯白噪声，采用上述4种方法得到的去噪图像与方法噪声如图6所示。由图6中的结果可以看出，原始NLM算法所得去噪图像被过度平滑，方法噪声中包含明显的图像结构信息；NLFMT算法所得方法噪声中的图像结构信息明显减弱，但仍清晰可见，所得去噪图像中含有小波基函数带来的伪影，视觉效果较差；PPB 25it与本文方法所得方法噪声中已看不出明显的图像结构特征，所得去噪图像的边缘及纹理结构清晰，如帽沿及帽穗部分，本文方法所得去噪图像中的细节特征更加自然。

4.4实际图像去噪实验

本文方法不依赖于原始图像，且噪声的方差可以由估计方法得到［20］，因此，该方法可以应用于对实际含噪图像的降噪处理。图7（a）所示是一幅实际的含噪图像，分别利用NLM及本文方法对其进行去噪，所得降噪图像如图7（b）和图7（c）所示。

由图7中的去噪结果可以看出，两种方法都能够有效地滤除噪声；与原始的NLM算法相比，本文方法能够更好地保留图像的细节信息，如树木的枝叶、瓦片的纹理、窗户的边缘等部分，如图7（c）中虚线框所标示，图7（d）和图7（e）给出了树木枝叶的局部放大图像。

图6　去噪图像与方法噪声比较

图7　实际图像去噪结果

5　结束语

本文提出了一种适用于NLM算法的残差图像多级滤波方法，该方法将残差图像滤波与NLM算法有机结合，能够充分地挖掘残差中的图像结构信息；基于去噪图像、残差图像与含噪图像之间的相关性，提出了一种无需参考图像的迭代停止准则，能够自适应地选择最佳滤波级数，得到与PSNR准则类似的评价效果；去噪过程无需参考图像，可应用于对实际含噪图像的降噪处理。实验结果表明，本文方法能够显著地提升非局部均值算法的去噪性能，且具有更好的细节保持能力。

本文从图像信息提取与去噪效果评价两个方面有效地利用了残差图像提供的信息。由此可见，残差图像在提升去噪算法的性能方面具有良好的潜力，探索更加有效且通用的残差图像滤波方法，是下一步需要开展的工作。

［1］BUADESA，COLL B，and MOREL JM.A review of image denoising algorithm s，w ith a new one［J］.Multiscale Modeling and Simulation（SIAM Interdisciplanary Journal），2005，4（2）: 490-530.doi:10.1137/040616024.

［2］钟莹，杨学志，唐益明，等.采用结构自适应块匹配的非局部均值去噪算法［J］.电子与信息学报，2013，35（12）:2908-2915. doi:10.3724/SP.J.1146.2013.00099.

ZHONG Ying，YANG Xuezhi，TANG Yim ing，etal.Non-local means denoising derived from structure-adap ted block matching［J］.JournalofElectronics&Information Technology，2013，35（12）:2908-2915.doi:10.3724/SP.J.1146.2013.00099.

［3］SUTOUR C，DELEDALLE C A，and AUJOL J F.Adaptive regularization of the n l-means:app lication to image and video denoising［J］.IEEE Transactions on Image Processing，2014，23（8）:3506-3521.doi:10.1109/TIP.2014.2329448.

［4］LU Lu，JIN W eiqi，and WANG Xia.Non-localm eans im age denoising w ith a soft threshold［J］.IEEE Signal Processing Letters，2015，22（7）:833-837.doi:10.1109/LSP.2014.2371332.

［5］DABOV K，FOI A，KATKOVNIK V，et al.Im age denoising by sparse 3D transform-domain collaborative filtering［J］. IEEE Transactions on Im age Processing，2007，16（8）: 2080-2095.doi:10.1109/TIP.2007.901238.

［6］DELEDALLE C A，DENISL，and TUPIN F.Iterativeweighted maximum likelihood denoising w ith probabilistic patch-based weights［J］.IEEE Transactions on Image Processing，2009，18（12）: 2661-2672.doi:10.1109/TIP.2009.2029593.

［7］罗亮，冯象初，张选德，等.基于非局部双边随机投影低秩逼近图像去噪算法［J］.电子与信息学报，2013，35（1）:99-105.doi: 10.3724/SP.J.1146.2012.00819.

LUO Liang，FENG Xiangchu，ZHANG Xuande，et al.An image denoisingmethod based on non-local two-side random projection and low rank approximation［J］.Journal of Electronics&Information Technology，2013，35（1）:99-105. doi:10.3724/SP.J.1146.2012.00819.

［8］TALEBI H and M ILANFAR P.Global image denoising［J］. IEEE Transactions on Im age Processing，2014，23（2）:755-768. doi:10.1109/TIP.2013.2293425.

［9］LIU Ganchao，ZHONG Hua，and JIAO Licheng.Com paring noisy patches for image denoising:a double noise sim ilarity model［J］.IEEE Transactions on Image Processing，2015，24（3）: 862-872.doi:10.1109/TIP.2014.2387390.

［10］FENG Jianzhou，SONG Li，HUO Xiaom ing，et al.An optim ized pixel-w ise weighting approach for patch-based image denoising［J］.IEEE Signal Processing Letters，2015，22（1）:115-119.doi:10.1109/LSP.2014.2350032.

［11］BRUNET D，VRSCAY E R，and WANG Z.The use of residuals in image denoising［C］.Proceedings of the International Conference on Image Analysis and Recognition，Halifax，2009:1-12.doi:10.1007/978-3-642-02611-9_1.

［12］CHEN J，TANG C K，and WANG J.Noise brush:interactive high quality image noise separation［J］.ACM Transactions on Graphics，2009，28（5）:146:1-10.doi:10.1145/1618452.1618492.

［13］PYO Y，PARK RH，and CHANG S.Noise reduction in high-iso images using 3-d collaborative filtering and structure extraction from residual blocks［J］.IEEE Transactions on Consum er Electron ics，2011，57（2）:687-695.doi:10.1109/ TCE.2011.5955209.

［14］ZHONG H，YANG C，and ZHANG X H.A new weight for nonlocalm eans denoising using m ethod noise［J］.IEEE Signal Processing Letters，2012，19（8）:535-538.doi:10.1109/ LSP.2012.2205566.

［15］KUMAR B K S.Im age denoising based on non-local m eans filter and itsm ethod noise th resholding［J］.Signal，Im age and Video Processing，2012，7（6）:1211-1227.doi:10.1007/ s11760-012-0372-7.

［16］ROMANO Y and ELAD M.Imp roving K-SVD denoising by post-processing its method noise［C］.IEEE International Conference on Image Processing，Melbourne，2013:435-439. doi:10.1109/ICIP.2013.6738090.

［17］ROMANO Y and ELAD M.Boosting of image denoising algorithm s［J］.SIAM Journal on Imaging Sciences，2015，8（2）: 1187-1219.doi:10.1137/140990978.

［18］KONG X F，LI K，YANG Q X，et al.A new image quality metric for im age au to-denoising［C］.14th IEEE International Conference on Com puter Vision，Sydney，2013:2888-2895.doi: 10.1109/ICCV.2013.359.

［19］WANG Z，BOVIK A C，SHEIKH H R，et al.Image quality assessment:From error visibility to structural sim ilarity［J］. IEEE Transactions on Image Processing，2004，13（4）:600-612. doi:10.1109/TIP.2003.819861.

［20］CHANG SG，YU B，and VETTERLIB.Adaptive wavelet thresholding for image denoising and com pression［J］.IEEE Transactions on Image Processing，2000，9（9）:1532-1546.doi: 10.1109/83.862633.

孙伟峰：男，1982年生，副教授，研究方向为图像处理、目标跟踪.

戴永寿：男，1963年生，教授，研究方向为故障诊断与智能信息处理、计算机测控技术.

Non-local Means Image Denoising with Multi-stage Residual Filtering

SUN Weifeng DAIYongshou
（Co llege of Inform ation and Con trol Engineering，China University of Petroleum，Qingdao 266580，China）

In order to sufficiently exploit the image in formation residing in the residual image for boosting the denoising performance of the Non-local Means（NLM）algorithm，a novelmulti-stage residual filtering method is proposed.Firstly，the Non-LocalMeans algorithm is applied to a noisy image to p roduce an initial denoised image and a weight distributingmatrix.Then the fixed-weight NLM algorithm is app lied to the residual image followed by a Gaussian filtering p rocess，which can extract the im age conten t ou t from the residualas a com pensation im age. The com pensation image is then added back to the denoised im age to generate an enhanced restored im age.An iterative scheme，whose p rincip le and feasibility are derived and p roved theoretically，is developed for the above filtering p rocedure；meanwhile a novelstopping criterion with no reference image required isp roposed to determ ine the op timal number of iterations adaptively.Experimental results demonstrate that the proposed stopping criterion behaves sim ilarly as the PSNR ru le，and compared w ith theoriginalNLM approach，the p roposed method can boost the denoising performance significantly w ith 1.2 dB PSNR gains achieved on average and m ore detail inform ation p reserved，w hile the com putational com p lexity is not apparently increased.

Image denoising；Non-LocalMeans（NLM）；Residual filtering；Stopping criterion

TN911.73

A

1009-5896（2016）08-1999-08

10.11999/JEIT 151227

2015-11-03；改回日期：2016-03-04；网络出版：2016-04-14

孙伟峰sw f0217@163.com

国家自然科学基金（61501520），山东省自然科学基金（ZR2013FL035），中央高校基本科研业务费专项资金（14CX 02083A）Foundation Item s:The National Natu ral Science Foundation of China（61501520），Shandong Provincial Natural Science Foundation（ZR2013FL035），The Fundamental Research Funds for the Central Universities（14CX 02083A）