大功率空心杯异步电机的参数计算与试验验证

倪守辉　王善铭　黄子果

(电力系统及发电设备控制和仿真国家重点实验室(清华大学)　北京　100084)



大功率空心杯异步电机的参数计算与试验验证

倪守辉王善铭黄子果

(电力系统及发电设备控制和仿真国家重点实验室(清华大学)北京100084)

空心杯异步电机虽然存在励磁电流大、功率因数低的不足，但其具有转子结构简单、可靠性高、转子无铁心、转动惯量小的突出优点，因此其在一些特殊要求的应用场合仍具有实用价值和应用前景。为了对空心怀异步电机进行性能分析和优化设计，必须能准确计算电机的参数。给出了空心杯异步电机的参数计算方法，通过解析法推导了转子阻抗的计算公式。在专门的试验电机上进行了参数测量，并将计算结果与测量结果进行了对比，此外还将负载试验测得的端口阻抗与计算参数和测量参数计算得到的端口阻抗进行了对比。对比结果证明了计算和分析的正确性。

空心杯异步电机参数计算试验

0　引言

空心杯电机因为转子上无铁心且只有绕组，所以转动惯量小，在很多高响应速度伺服系统中得到广泛使用[1-3]。空心杯电机包括空心杯直流电机[4]和空心杯异步电机[5]，其中空心杯异步电机实际应用较多的是空心杯测速发电机[5-8]。空心杯测速发电机在定子上布有励磁绕组和测量绕组，转子杯是整体导电杯。空心杯测速发电机工作时，在励磁绕组两端加交流电压，通过测量绕组中的感应电动势得到转子杯的转速。空心杯测速发电机的主要作用是将转速信号转换为电信号而不是实现机电能量的转换。

不同于空心杯测速发电机，本文研究对象为大功率空心杯异步电机，其定子绕组为三相绕组，用于实现机电能量转换。图1为空心杯异步电机横截面示意图。由于转子无铁心，转子质量轻，转动惯量小，响应速度快，控制性能好。另外，转子为整块导电杯，结构简单，可靠性较高。在高速系统中，由于转子杯质量小，减小了旋转部件质量不平衡来源，从而可减小振动。同时转子杯可与其他旋转部件一体化，这样能使系统的可靠性增加。在涡轮分子泵、汽车系统等快速响应应用场合中，空心杯异步电机具有很好的应用前景[9，10]。

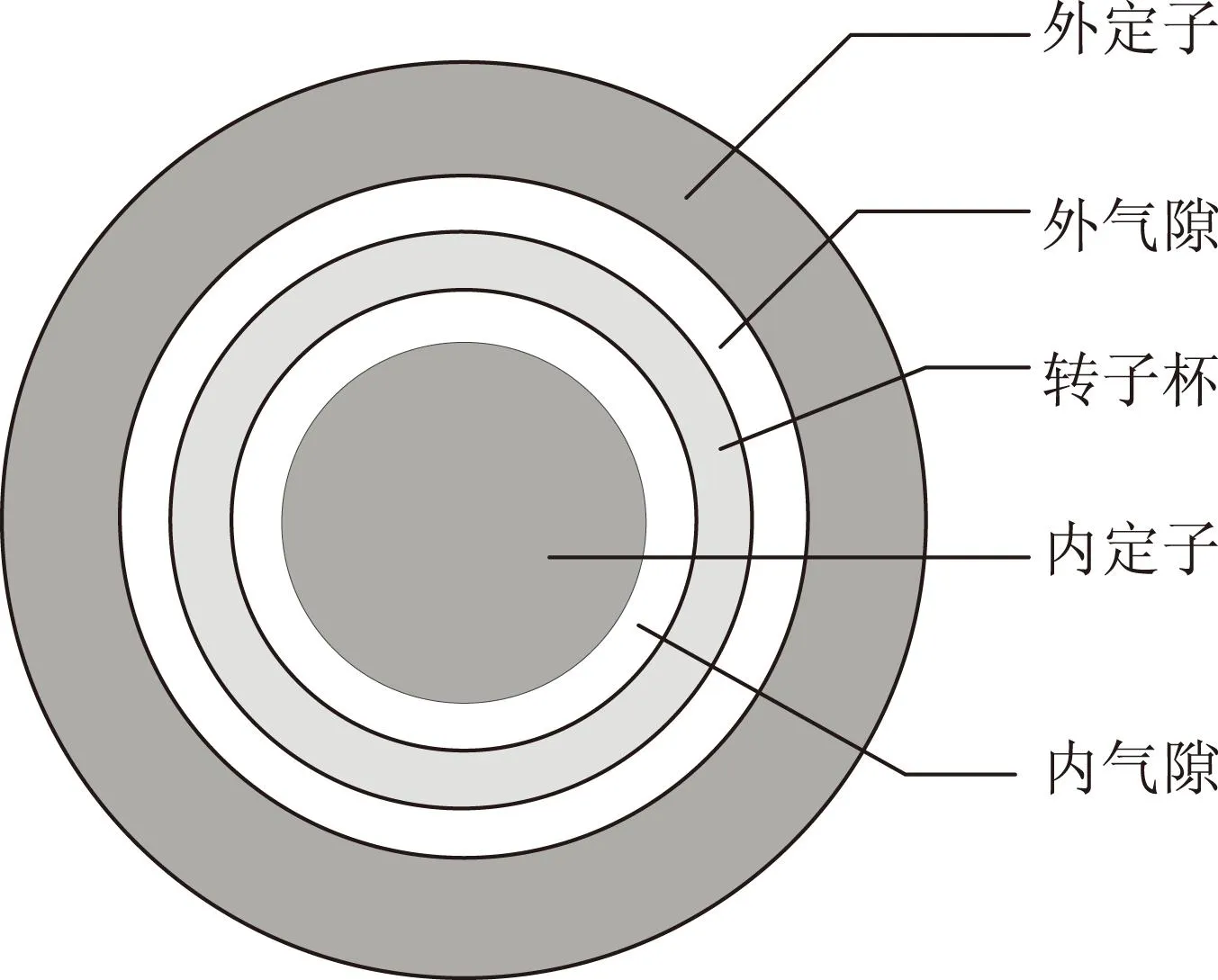
图1　空心杯异步电机横截面示意图Fig.1　Cross section of drag-cup induction machines

空心杯异步电机由于转子杯不导磁，且气隙存在内气隙和外气隙两个部分，等效气隙长度较长，因此功率因数较低，效率较低。为了对电机进行性能分析、优化设计、控制和保护，必须对电机的参数进行深入研究[11-14]。文献[15]中假定转子杯中有定子铁心覆盖的部分只存在轴向电流，转子杯两端伸出的部分只存在周向电流，在此基础上提出了转子带端环的空心杯异步电机的转子电阻的计算方法。文献[16]在求解边值问题的基础上，给出了空心杯异步电机转子电阻的表达式，但对转子电抗并未进行讨论，对转子电阻的计算结果也缺少直接的验证。文献[10]则利用有限元计算对空心杯异步电机的性能进行了分析，并将二维有限元和三维有限元的计算结果进行了对比，发现在转子杯和定子铁心长度一致的情况下，转子杯端部效应不可忽略。

空心杯异步电机的转子上没有固定的电流流通路径，这是其与普通异步电机的主要区别。而在电磁关系方面，空心杯异步电机与普通异步电机是类似的。本文在进行参数计算时，采用异步电机的T形等效电路模型[17，18]，如图2所示。考虑到空心杯电机等效气隙长度较长，气隙磁通密度一般较低，在等效电路模型中忽略了励磁电阻的作用。

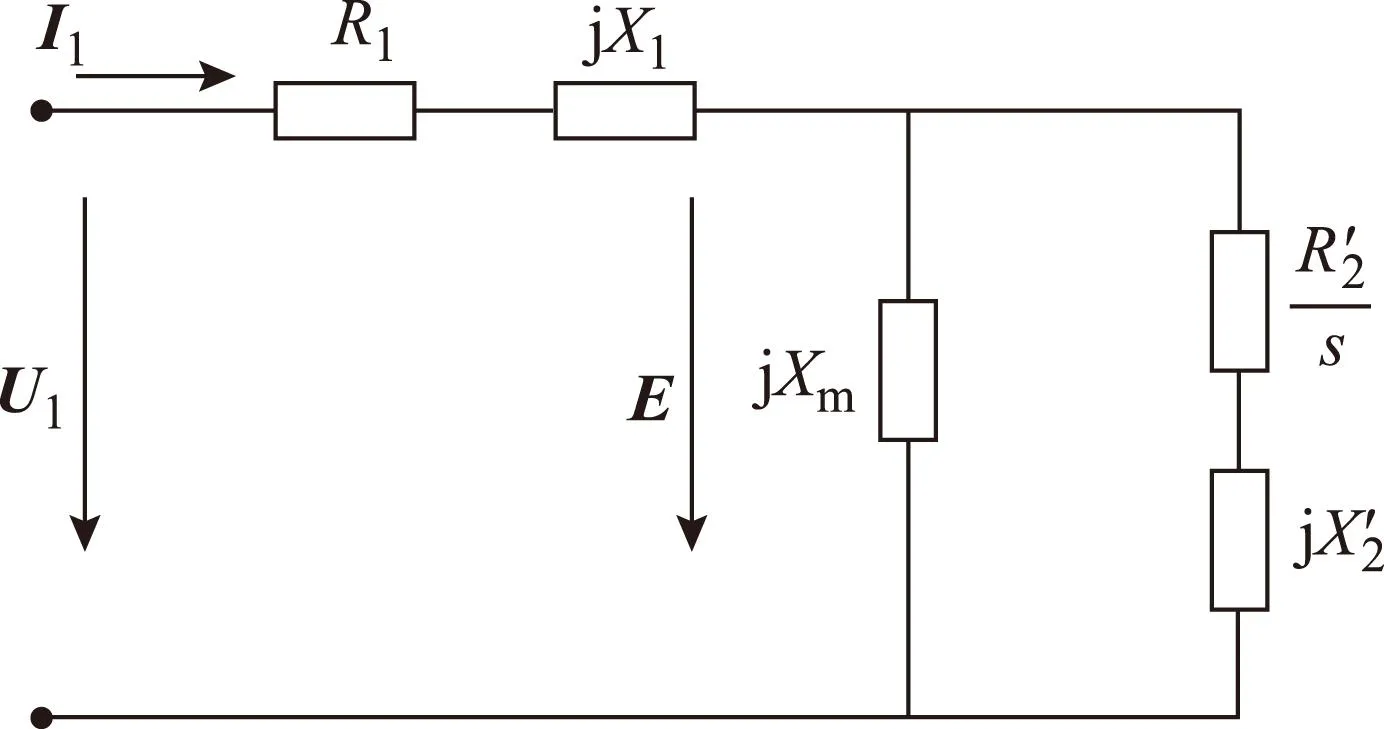
图2　空心杯异步电机T形等效电路Fig.2　T type equivalent circuit of drag-cup machines

本文给出了空心杯异步电机的定子电阻、定子漏抗和励磁电抗的计算公式，通过解析法推导了转子阻抗的计算公式。在专门的试验电机上进行了参数测量试验，将计算结果与测量结果进行了对比。此外为进一步验证，还对负载条件下的定子端口阻抗进行了测量，与计算参数和测量参数代入等效电路得到的端口阻抗进行了对比，对比结果证明了得到的试验参数的正确性。本文给出的参数都是解析形式，便于用于空心杯异步电机的设计和优化设计中。

1　定子参数与励磁电抗的计算

空心杯异步电机与普通异步电机定子侧相似，可采用普通异步电机的参数计算方法，计算空心杯异步电机的定子电阻、定子漏抗和励磁电抗。

定子电阻的计算公式为

(1)

式中，R1为定子相电阻；N1为定子每相串联匝数；a为定子并联支路数；ρ为定子绕组电阻率；l1为定子绕组半匝长度；Sc为定子导线截面积；Nc为定子并绕根数。

定子漏抗的计算公式为

(2)

式中，X1为定子漏抗；μ0为真空磁导率；f为定子频率；p为极对数；q为每极每相槽数；lef为铁心计算长度；λs为定子槽比漏磁导；λe为定子端部比漏磁导；λt为定子齿顶比漏磁导；λh为定子谐波比漏磁导。各漏磁导的计算可参见文献[19]。

励磁电抗的计算公式为

(3)

式中，Xm为励磁电抗；m1为定子相数；Kw为定子基波绕组因数；τ为对应转子杯平均半径的极距；δ为等效气隙长度。

2　转子参数计算

2.1求解域与基本假设

为了考虑端部的影响并简化分析，将转子杯沿周向方向展开成平面，并将转子等效为充满整个气隙，即有

(4)

式中，σe为转子等效电阻率;σ2为转子电阻率；d为转子厚度。

考虑到转子的对称性和周期性，求解区域圆周方向取一对极的范围，轴向取电机轴向长度的一半，如图3所示，其中y方向为圆周方向，z方向为电机的轴向，出纸面的x方向为电机的径向，图中未标出x方向。图3中τ为极距，L为定子铁心长度，Le为转子杯单边伸出的长度；Ⅰ区为定子铁心覆盖的转子部分，Ⅱ区为无定子铁心覆盖的部分，即为转子端部。

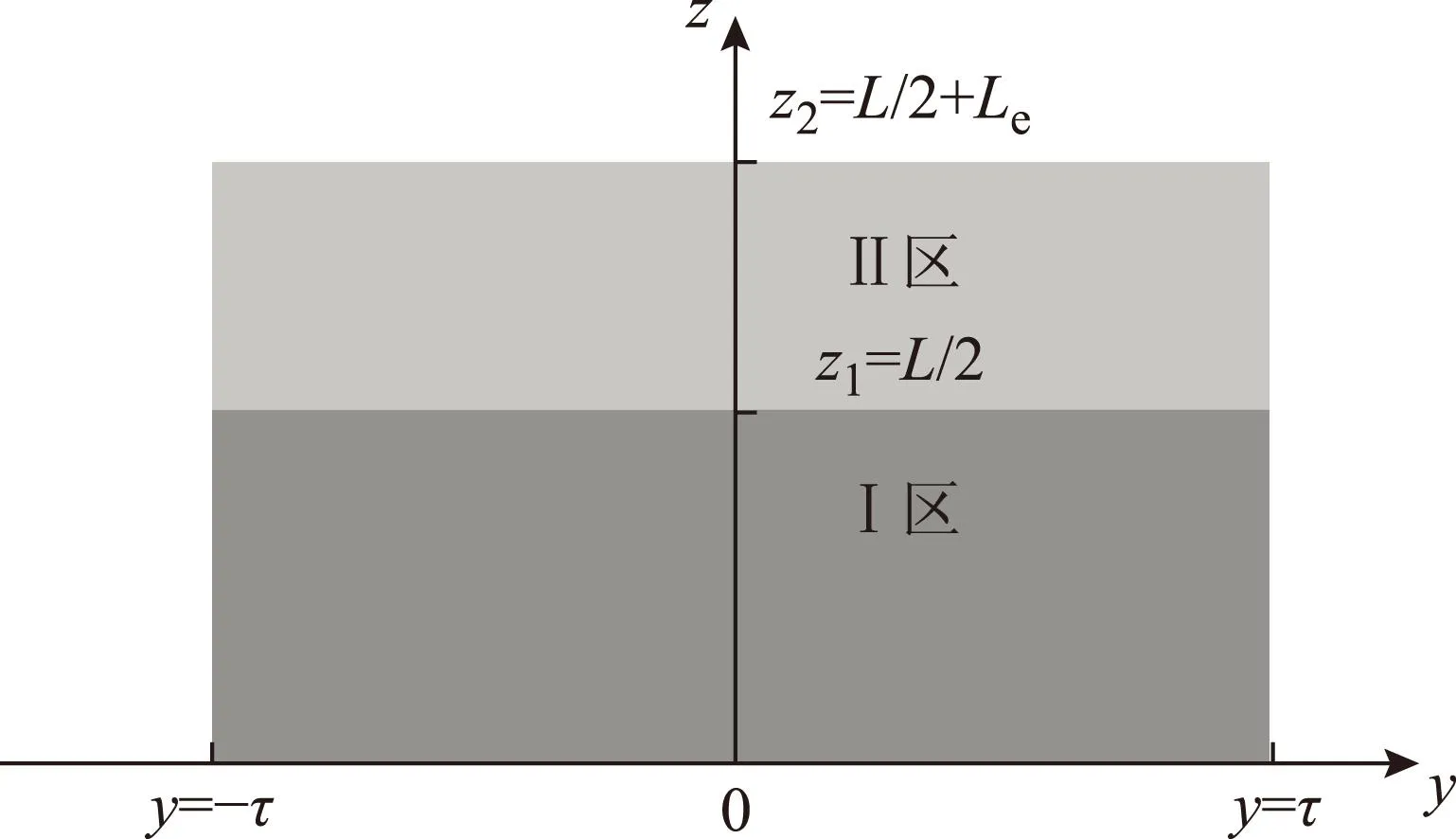
图3　求解区域Fig.3　Solving domain

在求解区域中，所有场量沿x方向均匀分布；所有场量均为正弦行波，幅值与y坐标无关；磁场只含有x分量，电场只含有y分量和z分量，在有定子铁心覆盖的部分即Ⅰ区存在一个由定子电流产生的外加H场，该H场为正弦行波，其分布与z坐标无关。

2.2边值问题的求解

为方便分析，令

(5)

在Ⅰ区中，设外加磁场强度为

Hs=Hmej(sωt-ky)

(6)

式中，s为转差率；ω为角频率。

设由转子电流产生的磁场强度为

Hr=Hpej(sωt-ky)

(7)

由麦克斯韦方程组可以导出Ⅰ区的磁场强度的方程为

(8)

方程的通解形式为

Hp=C1eλz+C2e-λz+CHm

(9)

式中，C1和C2为待定系数；λ和C的表达式分别为

(10)

(11)

Ⅰ区中电流密度的分布为

(12)

(13)

在Ⅱ区中，由于不存在外加磁场，则电位方程为拉普拉斯方程，令φ=φ(z)ej(sωt-ky)， 得到

(14)

方程的通解形式为

φ(z)=K1ekz+K2e-kz

(15)

式中，K1和K2为待定系数。

Ⅱ区中电流密度的分布为

(16)

(17)

式(9)和式(15)中的待定系数可通过边界条件来确定。

1)在z=0处，由于转子关于y轴对称，电流密度的y分量为0，由式(12)得

(18)

则有

C1=C2

(19)

2)在z=L/2+Le处，电流密度的z分量为0，由式(17)得

(20)

从而有

K2=K1ek(L+2Le)

(21)

3)在z=L/2的Ⅰ区和Ⅱ区分界处，Ⅰ区和Ⅱ区电流密度连续，由式(12)、式(13)、式(16)和式(17)得

jσek(K1ekL/2+K2e-kL/2)=λ(C1eλL/2-C2e-λL/2)

(22)

-σek(K1ekL/2-K2e-kL/2)=

jk[λ(C1eλL/2+C2e-λL/2)+CHm]

(23)

整理得

(24)

(25)

这样就得到了Ⅰ区的磁场强度和Ⅱ区的电位分布。

2.3转子阻抗计算

(26)

由于磁路相同，磁通与建立磁场的电流呈正比，所以Φs和Φδ的比值满足

(27)

在等效电路中有

(28)

由式(3)、式(26)、式(27)、式(28)整理得到

(29)

实际计算时，由于转子杯伸出了足够长，考虑到磁场的边缘效应，将转子杯有铁心覆盖部分的轴向长度等效增长2倍等效气隙长度，转子杯单边伸出的长度缩短1倍等效气隙长度，有

(30)

利用式(30)，结合式(4)、式(5)、式(10)、式(11)，便可计算出转子阻抗。

3　试验验证

3.1试验电机设计与基本参数

为了验证空心杯异步电机的参数计算方法，制造了一台铝杯异步电机进行试验。试验电机结构如图4所示。试验电机采用旋转电枢式结构，即电枢旋转，导电杯固定。这样可直接使用绕线转子异步电机的转子作为旋转电枢，方便试验电机的制造。为了方便叙述，下文中依然称旋转电枢为定子，铝杯为转子。试验电机的基本参数见表1。

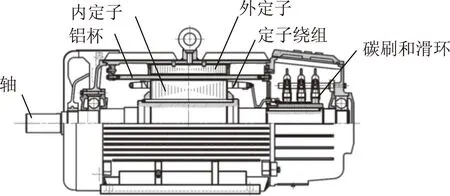
图4　试验电机结构Fig.4　The structure of the test machine

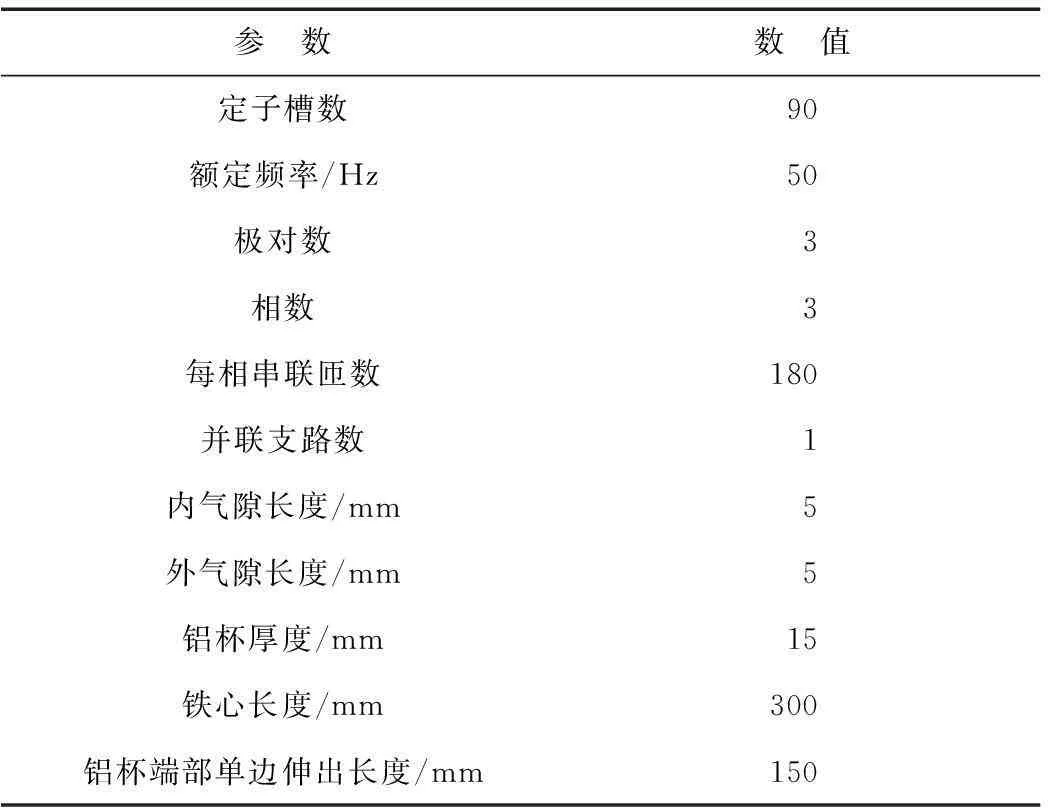
参 数数 值定子槽数90额定频率/Hz50极对数3相数3每相串联匝数180并联支路数1内气隙长度/mm5外气隙长度/mm5铝杯厚度/mm15铁心长度/mm300铝杯端部单边伸出长度/mm150

3.2本文计算方法得到的参数

采用第2节中的参数计算公式，计算得到的试验电机等效电路参数为：定子电阻0.51 Ω，励磁电抗5.9 Ω，定子漏抗2.32 Ω，转子电阻0.46 Ω，转子漏抗0.015 Ω，此处的电抗值均为定子频率50 Hz时的数值。

3.3通过试验测量参数

为了测量得到电机的参数，对试验电机进行堵转试验和转子同步速试验。进行同步速试验可得到严格空载情况下的试验数据，避免机械摩擦对参数测量造成影响。堵转试验共6组，定子频率从10 Hz变化到60 Hz，间距10 Hz。每组试验中控制定子电流从28 A均匀变化到5 A。同步速试验共3组，分别为：定子电压380 V，频率60 Hz，转速1 200 r/min；定子电压310 V，频率50 Hz，转速1 000 r/min；定子电压240 V，频率40 Hz，转速800 r/min。

在进行试验数据的分析时，对输入电压和电流波形进行傅里叶分解，得到电机输入端口的阻抗值。同步速试验时得到的端口电阻即为定子电阻，端口电抗即为励磁电抗与定子漏抗之和Xs。在堵转试验中，由T形等效电路可得到端口阻抗的表达式为

(31)

当定子频率较高时，励磁电抗远大于转子阻抗，此时近似有

(32)

取60 Hz堵转时得到的端口电抗作为定子漏抗与转子漏抗之和XL。考虑到高频时转子趋肤效应较明显，利用式(31)计算转子电阻时采用10 Hz堵转工况下的端口阻抗Ze1。

在试验测量中并未将定子漏抗和转子漏抗分开，从而难以直接得到定子漏抗、转子漏抗、励磁电抗、转子电阻等电路参数。利用3.2节中得到的定子漏抗和转子漏抗的比例，从XL中得到定子漏抗和转子漏抗。进一步地，从Xs中减去定子漏抗得到励磁电抗，由Ze1结合式(31)得到转子电阻。

从试验数据中测量得到的电路参数为：电枢电阻0.50 Ω，励磁电抗5.8 Ω，定子漏抗2.35 Ω，转子电阻0.48 Ω，转子漏抗0.015 Ω，电抗为50 Hz时的数值。

需要特别指出的是，试验测量的铁耗很小，这是因为试验电机的最大气隙磁通密度为0.1 T，气隙磁通密度很低。因此，在等效电路中忽略试验电机的励磁电阻的影响是合理的。

3.4负载试验与计算结果的对比与分析

为了进一步验证计算得到的参数的准确性，还进行了负载试验，利用计算和测量的参数计算负载情况下的端口等效电阻和等效电抗，与负载试验测量得到的端口电阻和电抗进行对比。负载试验共3组，分别为：定子电压380 V，频率60 Hz，转速1 200 r/min至1 120 r/min；定子电压310 V，频率50 Hz，转速1 000 r/min 至900 r/min；定子电压240 V，频率40 Hz，转速800 r/min至720 r/min。分别将本文计算方法计算得到的参数和试验测量得到的参数代入到T形等效电路中，计算出负载时的端口阻抗，与负载试验实际测得的端口阻抗值进行比较。

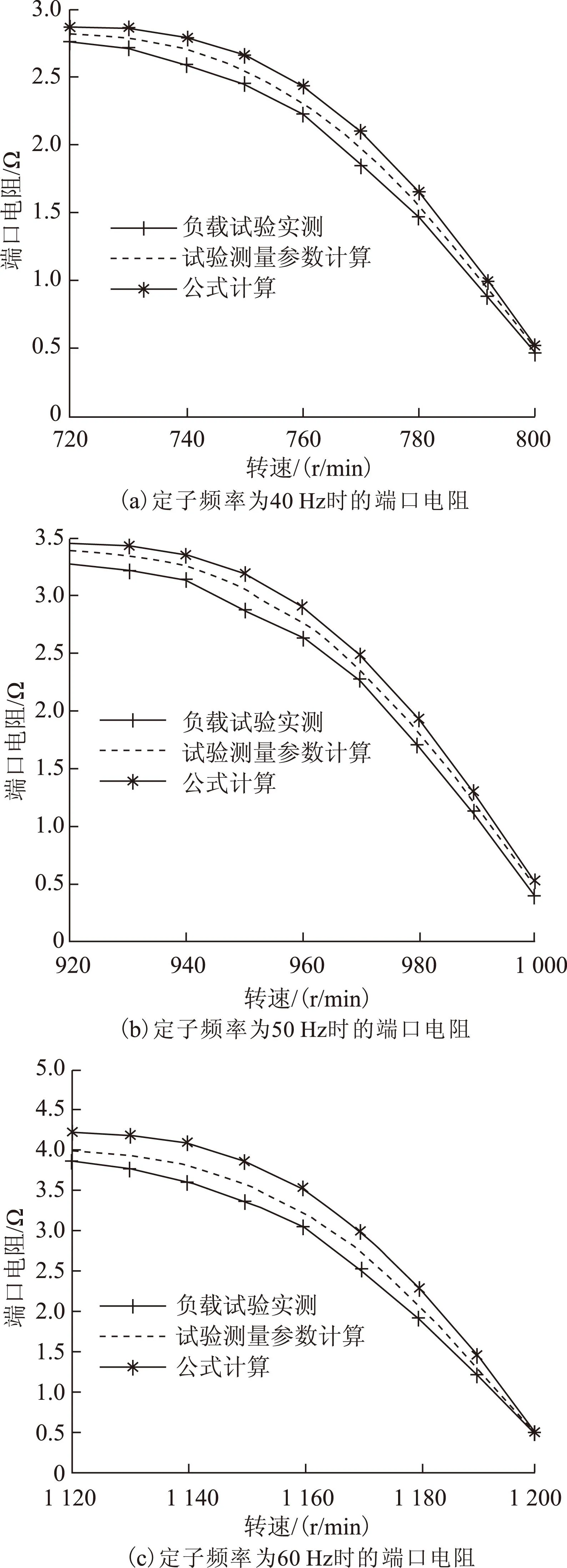
图5　定子端口电阻对比Fig.5　Comparison of the resistance of stator terminals

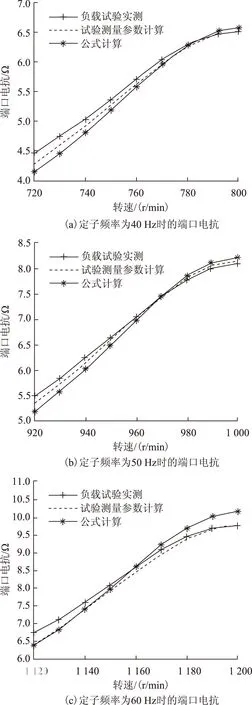
图6　定子端口电抗对比Fig.6　Comparison of the reactance of stator terminals

图5和图6分别给出了3种方法得到的端口电阻和端口电抗的比较，对比结果表明，本文计算方法计算得到的参数和试验测量的参数都是合理的。但与负载试验的测量结果相比较，通过公式计算和通过测量参数计算得到的端口电阻偏大，端口电抗也存在偏差,这样会导致进一步计算得到的功率因数和定子电流的误差。下面分别对两种方法误差产生的原因进行分析。

同步速试验和堵转试验的过程相对较短，定转子温升相对较低，而负载试验的过程较长，定转子温升相对较高。这样负载试验中实际的定转子电阻与通过同步速试验和堵转试验测得的定转子电阻相比要偏大,会对计算得到的端口电阻和端口电抗造成影响。式(32)中的近似也会对测量参数造成影响，从而影响端口电阻和端口电抗的计算。

在利用式(30)计算转子阻抗时，采用增加转子杯有铁心覆盖部分的轴向计算长度和减小转子杯端部伸出的计算长度的方法来等效气隙磁场的边缘效应。考虑到气隙长度较大，这样会引入转子阻抗的计算误差，从而导致计算得到的端口电阻和端口电抗的误差。另外，在计算励磁电抗时没有考虑曲率的影响，对计算结果也会造成影响。

4　结论

本文对空心杯异步电机T形等效电路参数进行了详细计算，特别是推导了转子参数的计算公式。设计制造了专门的试验电机，利用堵转试验和转子同步旋转试验测量了电机参数，将本文计算方法计算的参数与测量参数进行了对比。为了充分验证本文方法的正确性，还利用负载试验测量得到的定子端口等效阻抗与本文计算方法得到的参数和测量参数代入等效电路后得到的定子端口阻抗进行了对比，对比结果证明了本文计算和分析的正确性。本文的计算方法可应用于空心杯异步电机的设计和优化中。

[1]杜永红，邵定国，许路，等.基于三角形连接的空心杯电机无位置传感器控制方案[J].电机与控制应用，2008，35(6)：20-23.

Du Yonghong，Shao Dingguo，Xu Lu，et al.Sensorless control solutions based on delta-connection drag cup motor[J].Electric Machines & Control Application，2008，35(6)：20-23.

[2]方卫，杨香蕊，和苗.微型空心杯电机电磁兼容性研究[J].微电机，2013，46(12)：81-83.

Fang Wei，Yang Xiangrui，He Miao，et al.Research of electromagnetic compatibility for micro coreless motor[J].Micromotors，2013，46(12)：81-83.

[3]曾青山.面向外骨骼机器人的空心杯电机位置伺服控制研究[D].成都：电子科技大学，2013.

[4]姚永庆.水平井牵引机器人空心杯直流伺服电动机的研究[D].哈尔滨：哈尔滨工业大学，2006.

[5]徐荣泉，王双寿，张人群.异步测速发电机的剩余电压[J].微特电机，1976，1(1)：23-33.

Xu Rongquan，Wang Shuangshou，Zhang Renqun.Residual voltage of AC tacho-generators[J].Small & Special Electrical Machines，1976，1(1)：23-33.

[6]黄璞，王双寿，严关森.空心杯转子异步测速发电机的计算[J].微特电机，1976，1(4)：51-61.Huang Pu，Wang Shuangshou，Yan Guansen.Calculation of hollow cup AC tacho-generators[J].Small & Special Electrical Machines，1976，1(4)：51-61.

[7]吉崇庆，李仁发，王成山.异步测速发电机中转子漏抗对输出特性的影响[J].微电机，1985，1(3)：24-26.

Ji Chongqing，Li Renfa，Wang Chengshan.Influence of rotor leakage reactance on output characteristics in AC tacho-generators[J].Micromotors，1985，1(3)：24-26.

[8]Frazier R H.Analysis of the drag-cup AC tachometer by means of 2-phase symmetrical components[J].Transactions of the American Institute of Electrical Engineers，1951，70(2)：1894-1906.

[9]Bottauscio O，Casaro F，Chiampi M，et al.High-speed drag-cup induction motors for turbo-molecular pumps applications[J].IEEE Transactions on Magnetics，2006，42(10)：3449-3451.

[10]Terzic M V，Mihic D S，Vukosavic S N.Design of high-speed，low-inertia induction machines with drag-cup rotor[J].IEEE Transactions on Energy Conversion，2014，29(1)：169-177.

[11]王伟华，王红宇，许国瑞，等.基于时步有限元的抽水蓄能电机瞬态参数计算方法的对比[J].电工技术学报，2015，30(1)：89-97.

Wang Weihua，Wang Hongyu，Xu Guorui，et al.Contrastive study on calculation methods of transient parameters of pumped storage machine based on time-stepping finite element method[J].Transactions of China Electrotechnical Society，2015，30(1)：89-97.

[12]陈瑞广.分数槽集中绕组永磁同步电机的电感计算[J].电工技术学报，2014，29(3)：119-124.

Chen Ruiguang.Inductance calculation of permanent magnet synchronous machines with fractional-slot concentrated winding[J].Transactions of China Electrotechnical Society，2014，29(3)：119-124.

[13]杜治，马蕊，梁易乐，等.一种发电机励磁系统模型参数可辨识性分析方法[J].电力系统保护与控制，2014，42(22)：38- 44.

Du Zhi，Ma Rui，Liang Yile，et al.Analysis method on parameter identifiability for exciation system model of generator[J].Power System Protection and Control，2014，42(22)：38- 44.

[14]孙昊，王茂海，齐霞.基于PMU实测数据的同步发电机参数在线辨识方法[J].电力系统保护与控制，2014，42(3)：31-36.Sun Hao，Wang Maohai，Qi Xia.Synchronous generator parameters identification based on PMU data[J].Power System Protection and Control，2014，42(3)：31-36.

[15]Fuller B L，Trickey P H.Equivalent drag cup resistance[J].Transactions of the American Institute of Electrical Engineers，1962，81(3)：285-290.

[16]Fillmore R L.Calculation of eddy current paths in drag-cup induction motor rotors[J].Transactions of the American Institute of Electrical Engineers，1956，75(3)：922-926.

[17]姜杰，王学斌，殷家敏，等.基于感应电动机复数简化模型的参数辨识研究[J].电力系统保护与控制，2014，42(19)：87-92.

Jiang Jie，Wang Xuebin，Yin Jiamin，et al.Research on identification of induction motor based on its simplified complex quantity models[J].Power System Protection and Control，2014，42(19)：87-92.

[18]刘鹏，吴文进，苏建徽.一种异步电动机静止状态下参数辨识的改进方法[J].电工技术学报，2015，30(5)：42- 48.

Liu Peng，Wu Wenjin，Su Jianhui，et al.An improved parameters estimation algorithm for induction motor in the standstill state[J].Transactions of China Electrotechnical Society，2015，30(5)：42- 48.

[19]陈世坤.电机设计[M].北京:机械工业出版社，1990：50-63.

Parameter Calculation and Experimental Verification of High-Power Drag-Cup Induction Machines

Ni ShouhuiWang ShanmingHuang Ziguo

(State Key Lab oratory of Control and Simulation of Power System and Generation Equipments Dept.of Electrical EngineeringTsinghua UniversityBeijing100084China)

Despite the shortcomings of low power factor and high excitation current，drag-cup induction machines have practical values and prospects in some applications with special requirements，for their outstanding advantages of simple rotor structure，high reliability，coreless rotor and low rotor inertia.In order to analyze the performance and optimize the design of the machine，it is required that the parameters of the machine should be accurately calculated.This paper presents the method for calculating the parameters of drag-cup induction machines，and derives the formula of the rotor impedance using analytical method.Parameter measurement is conducted on a special test machine，and the calculated results are compared with the measured results.In addition，the impedances of the stator terminals are calculated from the calculated parameters and the measured parameters respectively，and are compared with the directly measured impedance of the load tests.The comparison results prove the validity of the calculation and analysis.

Drag-cup，induction machines，parameter calculation，experiment

2015- 04-15改稿日期2015- 06-18

TM315

倪守辉男，1990年生，硕士研究生，研究方向为电机设计与优化和电机磁场数值计算。

E-mail：nsh.dian82@163.com(通信作者)

王善铭男，1972年生，副教授，研究方向为特殊电机设计分析，发电机内部故障分析和电机电磁场分析。

E-mail：wangsm96@mails.tsinghua.edu.cn

国家自然科学基金资助项目(51177077)。