结构概率与非概率可靠度指标对应关系研究

夏　雨,张　娜,李　靖,徐　迪

(广西科技大学土木建筑工程学院， 广西柳州545000)



结构概率与非概率可靠度指标对应关系研究

夏雨,张娜,李靖,徐迪

(广西科技大学土木建筑工程学院， 广西柳州545000)

针对目前在[-1,1]区间内,由非概率可靠度理论无法判断结构的安全与失效的问题,基于3σ截断法则，建立概率可靠度指标与非概率可靠度指标之间的对应关系。由《建筑结构可靠度设计统一标准》(GB-50068-2001)规定的结构可靠性指标计算临界非概率可靠性指标，提出了非概率可靠度指标处于[-1,1]区间内的一种由临界非概率可靠度指标确定结构可靠性的方法，并结合算例验证了该方法的有效性。研究结果表明：利用概率可靠度指标与非概率可靠度指标间的对应转换关系，由临界非概率可靠度指标可有效处理非概率可靠性指标处于[-1,1]区间内的结构可靠性问题，以更方便地评价结构的安全度。

3σ截断法则；非概率可靠度指标；结构可靠性

0　引　言

可靠性是结构设计的基本问题，任何一项与结构设计有关的研究都涉及结构的可靠性。按照我国《工程结构可靠性设计统一标准》(GB50153-2008)的定义，结构可靠性为结构在规定的时间内、在规定的条件下，完成预定功能的能力[1]。

目前，结构可靠性理论主要发展成为概率可靠性、非概率可靠性分析和混合可靠性分析。20世纪40年代，Freudenthal[2]将概率论与数理统计学应用于结构安全度分析，迈出了结构概率可靠性分析的第一步。尹航等[3]给出了梯度投影算法解决非概率可靠性问题。祁武超等[4-5]提出基于区间分析的结构非概率可靠性优化设计。王睿星等[6]将概率可靠性方法与非概率可靠性方法作比较，认为在掌握原始数据较少的情况下，非概率可靠性方法是有优势的。姜潮等[7]基于概率可靠性模型和非概率可靠性模型，建立了一种新的可靠性分析的概率—非概率可靠性混合模型。樊建平等[8]提出空间搜索法来求解非概率可靠度指标。Gong Jinxin等[9]给出了结构可靠性的非梯度算法。非概率可靠度理论的发展促进其在各个研究领域的广泛应用，WANG Xiaojun等[10]提出损伤测量指标，把非概率可靠度理论用于损伤诊断。Guo Shuxiang等[11]利用区间模型理论，提出结构分析和设计的新方法。Meng Zeng等[12]结合非概率可靠度理论对薄壁强化壳体结构进行优化分析，取得了良好的效果。李兆军等[13]应用非概率可靠性理论，建立具有相关失效模式的水轮发电机组主轴系统非概率可靠性。Wang Qian等[14]构建了T-S模糊模型，通过算例分析显示在近似的非线性系统中有较高的精确性。

基于概率可靠性理论和非概率可靠性理论计算得到的是不同理论体系下对结构可靠性的描述。实际工程中，由于数据的随机性，信息不足以及结构状态中的模糊性等其他一些不确定性因素导致有时候只能计算出概率可靠度或者非概率可靠度。如果能找出概率可靠度指标与非概率可靠度指标的联系，就能从概率和非概率两个方面对结构安全度作出评价。例如：一个结构用概率可靠度理论来描述时，只知道它的失效程度，如果转换成非概率可靠度指标就可以具体知道结构是可靠还是不可靠；当用非概率可靠度指标描述抗力与荷载效应发生干涉的情况时，也即是非概率可靠性指标处于-1<η<1时，利用非概率可靠性的知识可以用积分法或者是几何面积比值的方法求解出非概率可靠度，这种情况的前提是需要知道非概率可靠度的安全范围，否则无法判断结构安全与失效。若是转化成概率就可以知道结构的失效概率，可以很容易得到非概率可靠度，从而判断出结构的安全情况，因此研究概率可靠度指标与非概率可靠度指标的联系就显得尤为重要。

1　概率可靠度指标与非概率可靠度指标的联系

1.1基于3σ截断法则下概率可靠度指标与非概率可靠度指标对应转换关系

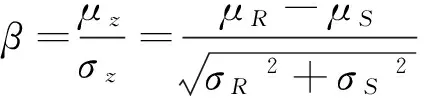
(1)

由非概率可靠度指标的定义：

(2)

由式(1)、式(2)则可以很容易得到β和η的关系：

(3)

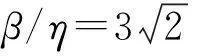
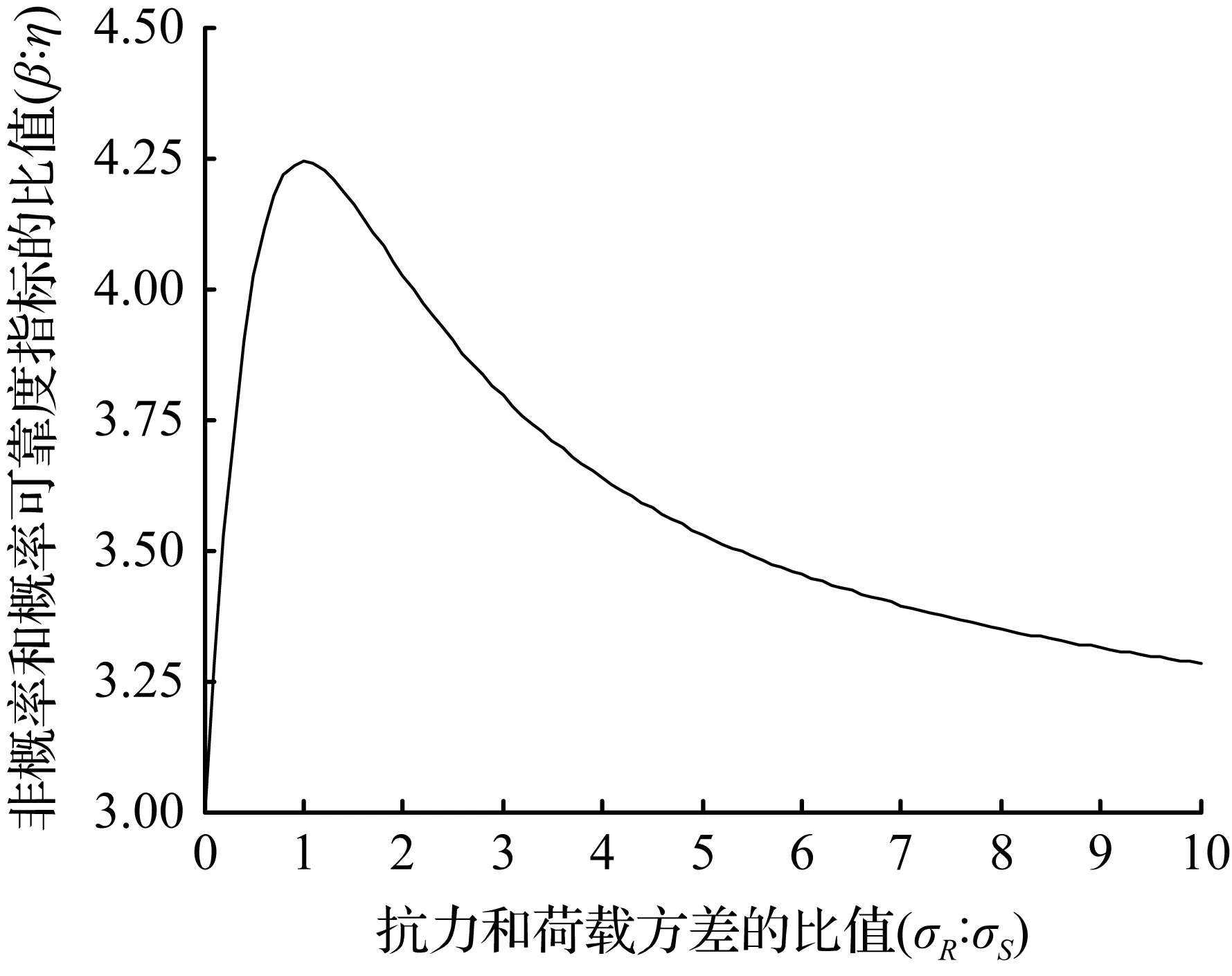
(a) [0,10]区间内非概率可靠度指标和概率可靠度指标关系

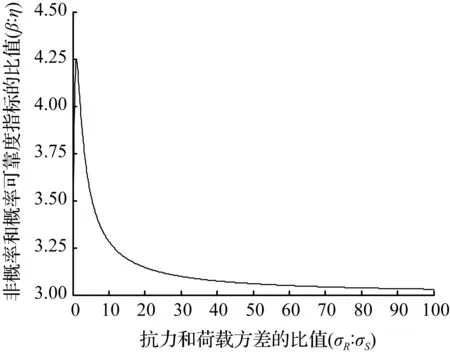
(b) [0,100]区间内非概率可靠度指标和概率可靠度指标关系

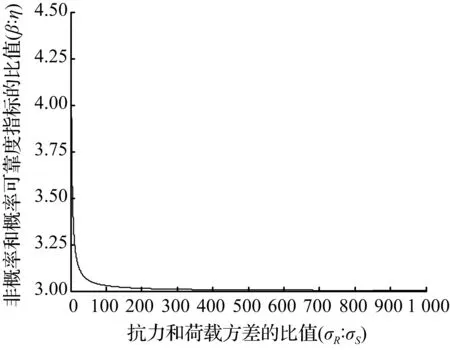
(c) [0,1 000]区间内非概率可靠度指标和概率可靠度指标关系

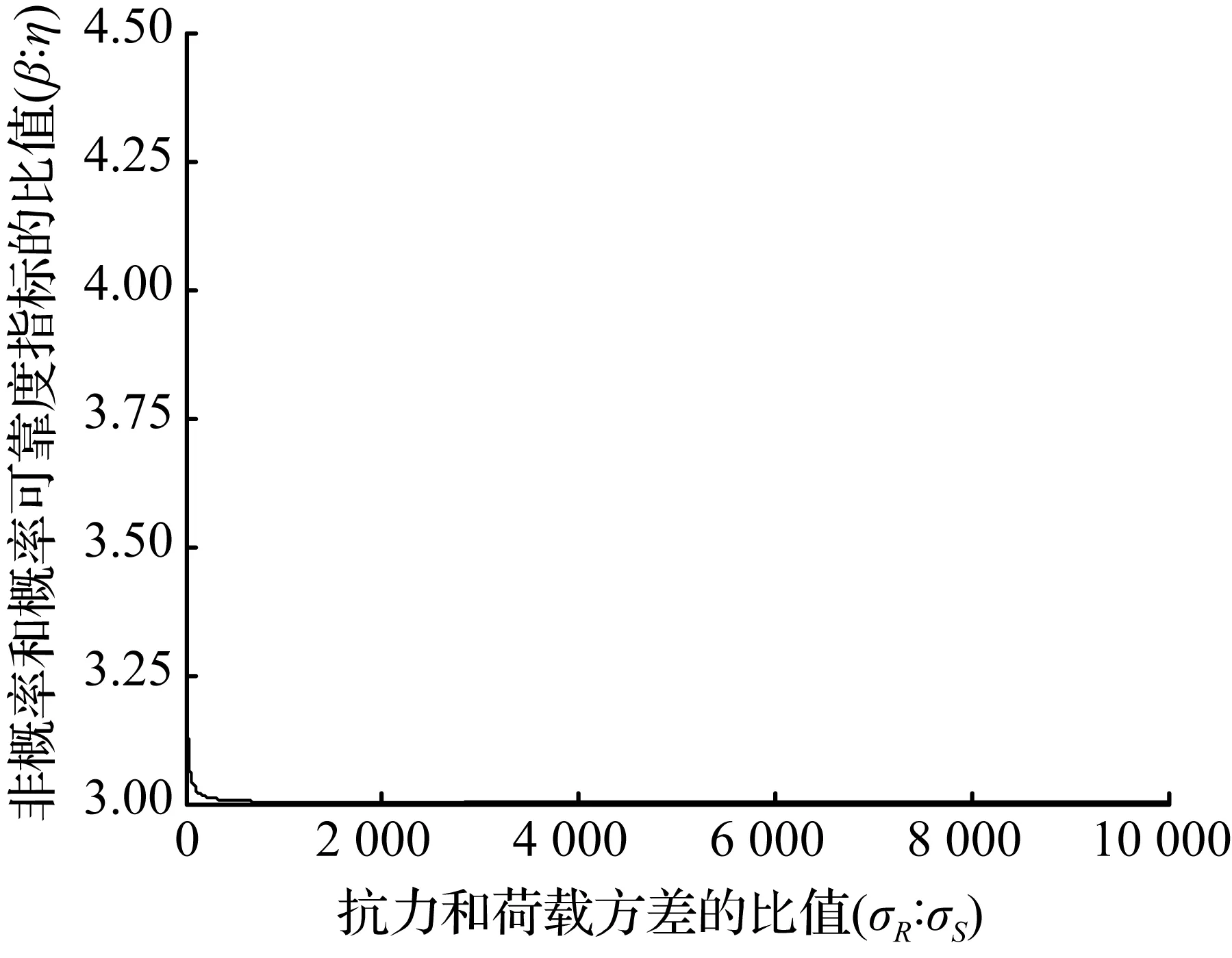
(d) [0,10 000]区间内非概率可靠度指标和概率可靠度指标关系

图13σ截断法则下σR∶σS和β∶η的关系

Fig.1The relationship betweenσR∶σSandβ∶ηunder the 3σrule

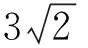
1.2定义域取(-∞,+∞)时概率可靠度指标与非概率可靠度指标对应转换关系

由概率论[15]的基本知识可知，变量R落在(μR-3σR,μR+3σR)之外的可能性还有0.26%，要使随机变量涵盖这0.26%，则正态随机变量的取值范围必须为(-∞,+∞)。要使随机变量取值为(-∞,+∞)，则抗力R和作用力S区间分布表示成R～(μR-nσR,μR+nσR)，S～(μS-nσS,μS+nσS), n∈N,n≥3，概率可靠度指标不变，而非概率可靠度指标则变为：

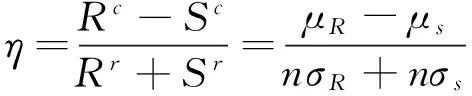
(4)

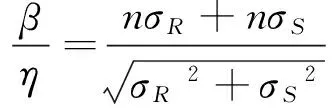
(5)

基于抗力R和荷载效应S离散程度比值变化规律下β/η的关系:

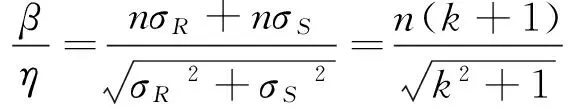
(6)

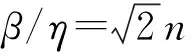
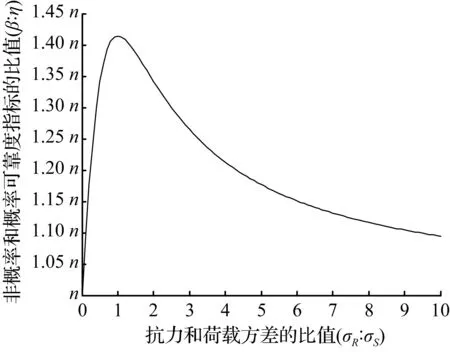
(a) [0,10]区间内非概率可靠度指标和概率可靠度指标关系

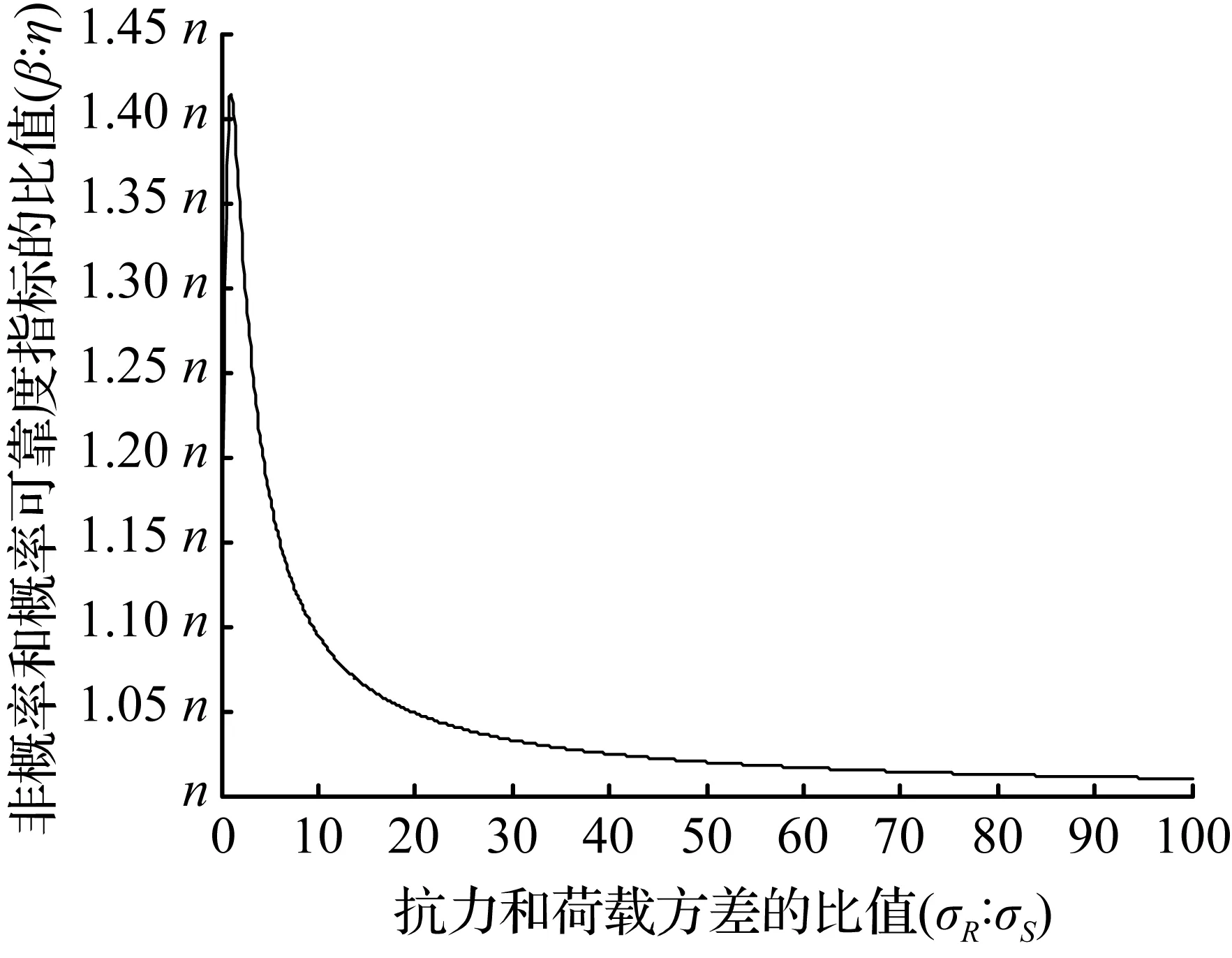
>(b) [0,100]区间内非概率可靠度指标和概率可靠度指标关系

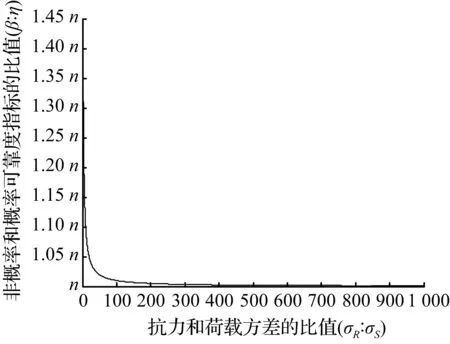
(c) [0,1 000]区间内非概率可靠度指标和概率可靠度指标关系

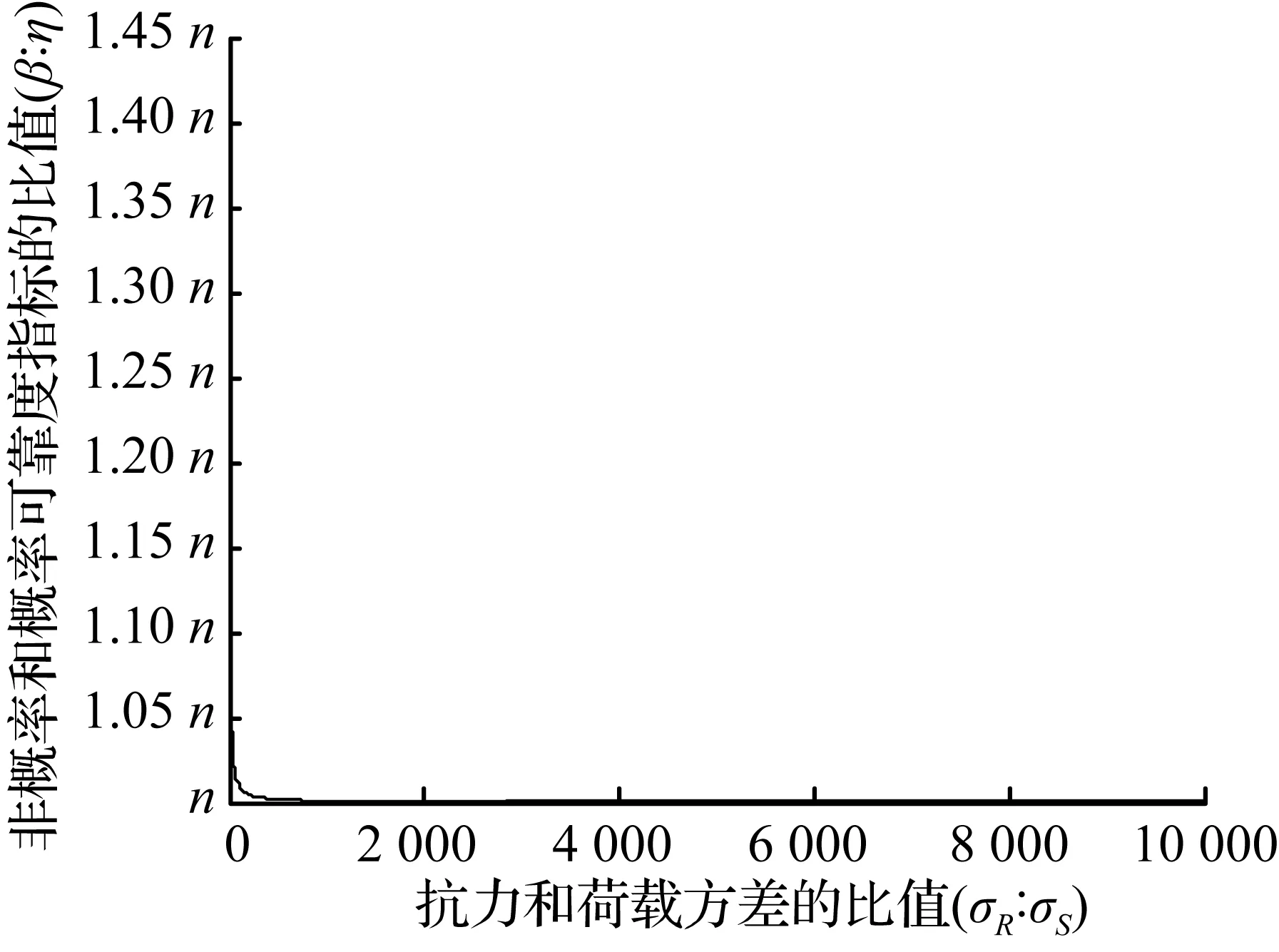
(d) [0,10 000]区间内非概率可靠度指标和概率可靠度指标关系

图2正态分布下σR∶σS和β∶η的关系

Fig.2The relationship betweenσR∶σSandβ∶ηunder the normal distribution

对比式(3)和式(6)发现：同一个结构，给定了期望和方差，概率可靠度指标β不变，随着n的增大(区间范围也增大)，不确定参数的离散程度也越大，概率可靠度指标与非概率可靠度指标之比也增大，非概率可靠度指标减小；也就是说变量区间越窄，η越高，非概率可靠性描述越安全(与概率可靠度描述越接近)；变量区间越宽，η越小，非概率可靠性描述越不安全(与概率可靠度描述越偏差大)。由此可得：基于非概率指标与概率可靠性指标的关系，可以得出非概率可靠度与概率可靠度描述的结构可靠度的适用性与安全性，合适的窄区间描述结构的非概率可靠性是符合工程实际的，而大区间描述往往是偏离概率可靠度的，此时用非概率可靠性指标去描述结构的可靠度是不符合实际的。

2　由临界非概率可靠度指标确定结构可靠性

结构功能函数表达式是M=R-S，抗力R和荷载效应S都服从正态分布，知道抗力R和荷载效应S各自的区间分布[RL,RR]和[SL,SR]，而此时通过区间变量计算出来的非概率可靠度指标是在[-1,1]区间内，此时无法判断结构可靠还是失效。

查《建筑结构可靠度设计统一标准》(GB-50068-2001)中3.0.11规定的结构构件承载能力极限状态设计时采用可靠度指标，是以建筑结构安全等级为二级时延性破坏的β值3.2作为基准，其他情况下相应增减0.5。可靠度指标β与失效概率的运算pf的关系见表1。

表1　可靠度指标及其对应的失效概率Tab.1　Reliability index and the corresponding failure probability

目标可靠度指标应综合各种因素，以优化方法确定。在公众心理，当结构在设计基准期内的失效概率在(1～7)×10-4(对应的β=3.2～3.7)的范围内，可以认为结构是安全的。通常定义一个建筑结构可以接受的失效概率为0.07%，将这个失效概率定义为结构临界失效概率，根据公式pf=Φ(-β)就可以求得临界概率可靠度指标βcr=3.2。

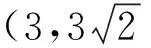
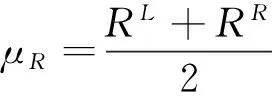
3　算例及其应用

一个结构其功能函数为M=R-S,其中抗力R服从区间分布[6,10]，同时荷载作用效应S服从区间分布[5,7]，试用非概率可靠度理论来判断结构所处的状态，或者用概率可靠度理论来描述结构的失效程度。

由非概率可靠度指标的定义，可求得非概率可靠度指标：

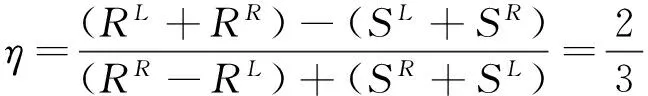
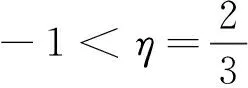
根据pf=Φ(-β)查正态分布表可得一个建筑结构概率可靠度指标临界点：

βcr=3.2。

抗力的方差与荷载效应方差之比k=2:

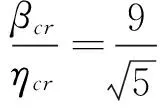
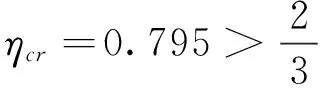
由此判定结构失效。

4　结　论

本文讨论了概率可靠度指标与非概率可靠度指标对应转换关系，并给出了其物理含义。然后研究了概率可靠度指标与非概率可靠度指标对应转换关系的应用，提出结合概率可靠度理论来解决非概率可靠性指标处于[-1,1]区间内无法确定结构可靠性的问题。基于非概率理论，本文运用概率可靠度指标与非概率可靠度指标的对应关系，结合我国《建筑结构可靠度设计统一标准》(GB-50068-2001)，通过转换，提出用临界非概率可靠度指标评价结构的安全程度的方法，并通过算例证明此方法的有效性。

[1]贡金鑫，魏巍巍，赵国藩.工程结构可靠性设计原理[M]. 北京: 机械工业出版社, 2007.

[2]FREUDENTHAL A M.The safety of structures[J]. Transactions of the American Society of Civil Engineers, 1947, 112:125-129.

[3]尹航，李世军，李小珍.梯度投影法的非概率可靠性应用研究[J]. 应用力学学报，2012，29 (6):718-722.

[4]祁武超，郑志平.基于区间分析的结构非概率可靠性优化设计[J]. 中国科学:物理学 力学 天文学，2013，43(1):85-93.

[5]王晓军，杨海峰，邱志平，等.基于非概率集合可靠性的结构优化设计[J]. 计算力学学报，2011，28 (6):827-832.

[6]王睿星，王晓军，王磊，等.几种结构非概率可靠性模型的比较研究[J]. 应用数学和力学，2013，34(8):871-880.

[7]姜潮，刘丽新，汤一飞.一种带区间变量混合模型的结构可靠性分析方法[J]. 汽车工程，2012，34(8): 727-732.

[8]樊建平，李世军，陈旭勇.非概率可靠性指标空间搜索算法[J]. 计算力学学报，2012，29(6): 831-840.

[9]GONG J X, YI P, ZHAO N.Non-gradient-based algorithm for structural reliability analysis[J]. Journal of Engineering Mechanics,2014,140(6): 682-694.

[10]WANG X J, XIA Y, ZHOU X Q.Structural damage measure index based on non-probabilistic reliability model[J]. Journal of Sound and Vibration, 2014, 333: 1344-1355.

[11]GUO S X, LU Z Z.A non-probabilistic robust reliability method for analysis and design optimization of structures with uncertain-but-bounded parameters[J]. Applied Mathematical Modeling, 2015,39: 1985-2002.

[12]MENG Z, HAO P, LI G, et, al.Non-probabilistic reliability-based design optimization of stiffened shells under buckling constraint[J]. Thin-Walled Structures, 2015,94:325-333.

[13]李兆军，刘福秀，邱旻，等.混流式水轮发电机组非概率可靠性模型[J]. 广西大学学报(自然科学版)，2014，39(2):258-264.

[14]WANG Q, SU Z G, BABAK R, et al.Constructing T-S fuzzy model from imprecise and uncertain knowledge represented as fuzzy belief functions[J]. Neurocomputing, 2015, 166:319-33.

[15]RAO M M.Probability theory with applications[M]. New York: Academic Press, 1984.

(责任编辑唐汉民梁健)

The relationship between probabilistic and non-probabilistic reliability index of structure

XIA Yu， ZHANG Na， LI Jing， XU Di

(School of Civil Engineering and Architecture, Guangxi University of Science and Technology, Liuzhou 545000, China)

When the non-probabilistic reliability index falls in the range of [-1, 1], it is unable to determine whether the structure is safe or not with the non-probabilistic reliability theory. Based on the 3σrule, the relationship between the probabilistic reliability index and the non-probabilistic reliability index is established. According to Unified Standard for Reliability Design of Building Structures (GB-50068-2001), a method to determine the safety of a structure based on the non-probabilistic reliability index when it is between -1 and 1 is proposed. An example proves the effectiveness and correctness of the proposed method. The study also shows that it is convenient to determine the structure’s safety by using the relationship of the probabilistic and the non-probabilistic reliability index.

3σ rule; non-probabilistic reliability index; structure reliability

2016-01-10；

2016-06-04

国家自然科学基金资助项目(51569005,51469005);广西自然科学基金资助项目(2015GXNSFAA139279)；广西研究生教育创新计划资助项目(YCSZ2015207)

夏雨(1979—)，男，河南南阳人，广西科技大学副教授，博士；E-mail：summ-rain@163.com。

10.13624/j.cnki.issn.1001-7445.2016.1279

TB114.3

A

1001-7445(2016)04-1279-06

引文格式：夏雨,张娜,李靖,等.结构概率与非概率可靠度指标对应关系研究[J].广西大学学报(自然科学版)，2016，41(4)：1279-1284.