三维Wilson元及在近不可压弹性问题中的应用

李真有,肖映雄

(湘潭大学土木工程与力学学院， 湖南湘潭411105)



三维Wilson元及在近不可压弹性问题中的应用

李真有,肖映雄

(湘潭大学土木工程与力学学院， 湖南湘潭411105)

为克服三维近不可压缩问题的体积闭锁现象，建立了两种基于六面体单元的Wilson非协调元计算格式，并将其应用于两类含混合边界条件的近不可压缩弹性问题的求解。数值结果表明:Wilson非协调元能有效克服三维体积闭锁现象，与相同规模下的协调元相比较，它具有更高的计算精度。在三维有限元分析中，剖分网格的质量将对计算精度影响很大，实际计算时若能采用各向同性网格，则对问题的分析将具有更好的收敛性。

近不可压缩问题；体积闭锁；Wilson非协调元；网格质量

利用通常的低阶协调有限元方法处理三维近不可压缩问题常出现体积闭锁现象。克服这种闭锁现象的方法很多，如混合有限元法[1-3]，非协调有限元法[4-6]，高阶协调元法[7-8]及减缩积分法[9-10]等。减缩积分使单元刚度矩阵秩降低，常引起多余的零能模式。与基于H-R变分原理的混合元格式相比，基于能量泛函极小的离散变分问题更容易被解决，并且有限元方程的系数矩阵是正定的，将给求解带来很大方便。对三维问题，若利用高阶协调元方法，要求单元阶次p≥8，这在实际计算中是不可取的。此时，常采用低阶非协调元(如二次元、线性元)来克服三维近不可压缩问题的闭锁现象[5,11]，这种方法具有自由度少、精度高的特点，可解决三维问题计算规模过大的困难。

在三维有限元分析中，常采用六面体网格剖分，这种网格在计算精度、划分数量、抗畸变程度等方面比四面体网格具有明显的优势。基于六面体单元的Wilson非协调元，它通过在单元内部设置附加自由度，以提高完全多项式的次数、改善计算精度。关于Wilson元的研究和应用，已有很多研究成果[12-15]。本文建立了两种基于六面体单元的Wilson非协调元，并将其应用于悬臂梁和Cook膜两类近不可压缩弹性问题的求解。数值结果表明：Wilson非协调元能有效克服三维体积闭锁现象，与相同规模下的协调元相比较，它具有更高的计算精度。还研究了有限元网格质量对Wilson元计算精度的影响，计算中若能采用各向同性网格，则对问题的分析将具有更好的收敛性。

1　近不可压缩问题和体积闭锁现象

考虑下述三维线弹性力学模型:

(1)

其中，Ω⊂R3，∂Ω=Γ0∪Γ1且Γ0∩Γ1=Φ, u为位移向量，f为外力，g为边界Γ1上的面力，n为边界Γ1的单位外法线向量，拉梅常数λ和μ可分别用杨氏模量E和泊松比ν表示为:

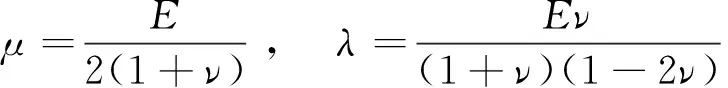
(2)

这里，泊松比ν∈[0,0.5)，当ν→0.5时，称相应的弹性力学问题为近不可压缩问题。

记Hm(Ω)={v|∂αv∈L2(Ω),|α|≤m}，则问题(1)对应的变分问题可描述为：

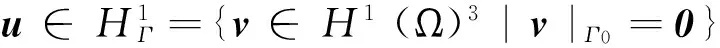
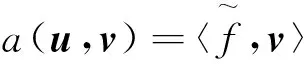
(3)

在有限元分析中，网格的划分及单元的选取是影响其计算精度的重要因素。四面体网格和六面体网格是三维有限元分析中常采用的两种网格类型，而六面体网格在计算精度、网格数量、抗畸变程度等方面比四面体网格具有明显的优势，已成为三维有限元分析中的首选网格。设Th是区域Ω上的六面体网格剖分，其中h为Th上所有剖分单元的最大直径。引入如下p次拉格朗日有限元空间：

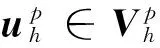
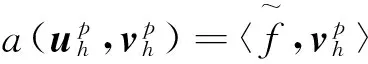
(4)

设变分问题(4)的p次有限元离散化线性系统的矩阵形式为:

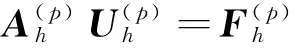
(5)

对近不可压缩问题，通常的低阶协调元(如三线性元、三二次元)解不再收敛到原问题的解或达不到最优收敛阶，即出现所谓的体积闭锁现象。下面，举两个例子来进行验证。

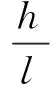
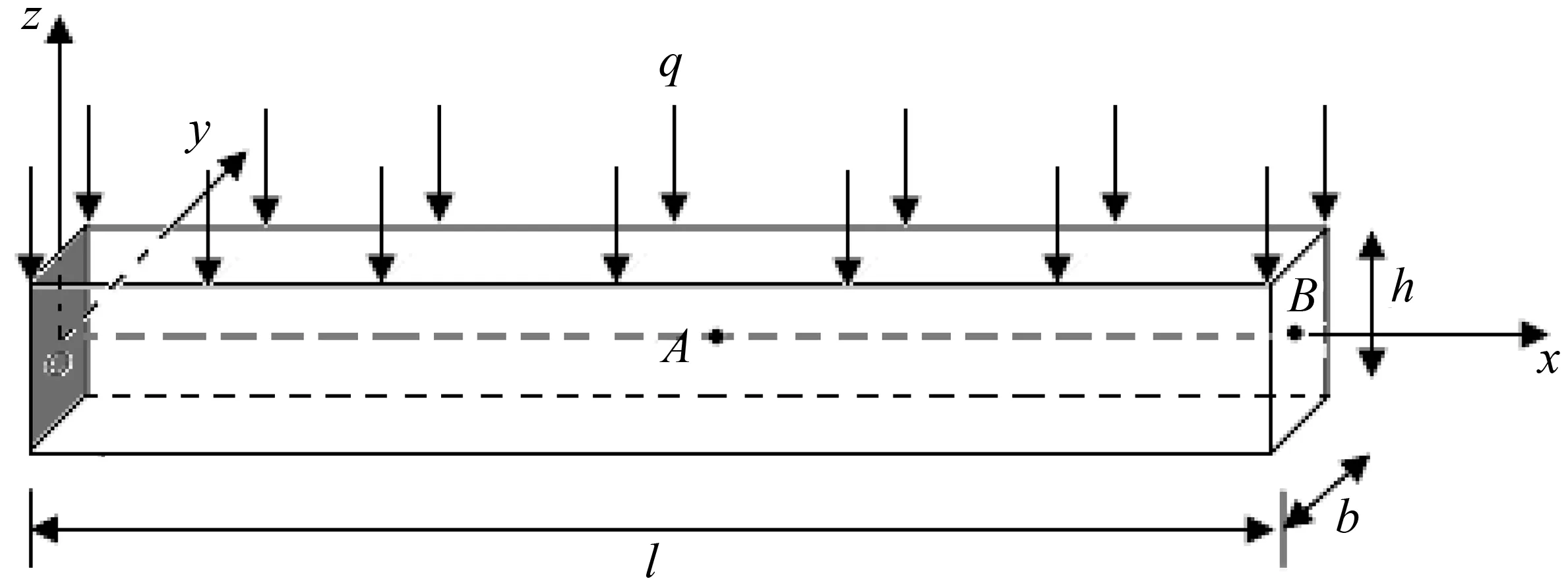
图1　悬臂梁几何结构示意图

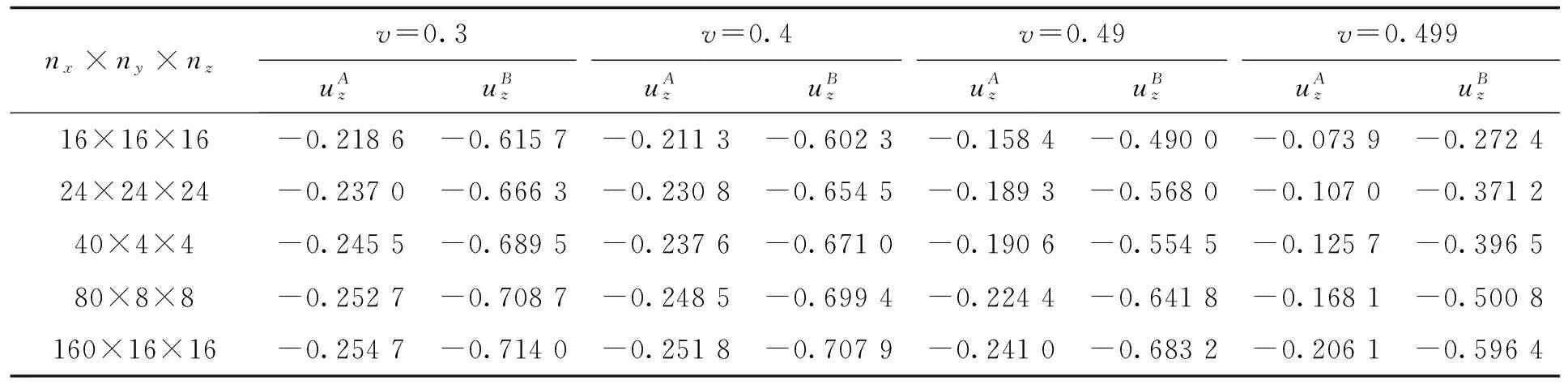
nx×ny×nzv=0.3v=0.4v=0.49v=0.499uAzuBzuAzuBzuAzuBzuAzuBz16×16×16-0.2186-0.6157-0.2113-0.6023-0.1584-0.4900-0.0739-0.272424×24×24-0.2370-0.6663-0.2308-0.6545-0.1893-0.5680-0.1070-0.371240×4×4-0.2455-0.6895-0.2376-0.6710-0.1906-0.5545-0.1257-0.396580×8×8-0.2527-0.7087-0.2485-0.6994-0.2244-0.6418-0.1681-0.5008160×16×16-0.2547-0.7140-0.2518-0.7079-0.2410-0.6832-0.2061-0.5964

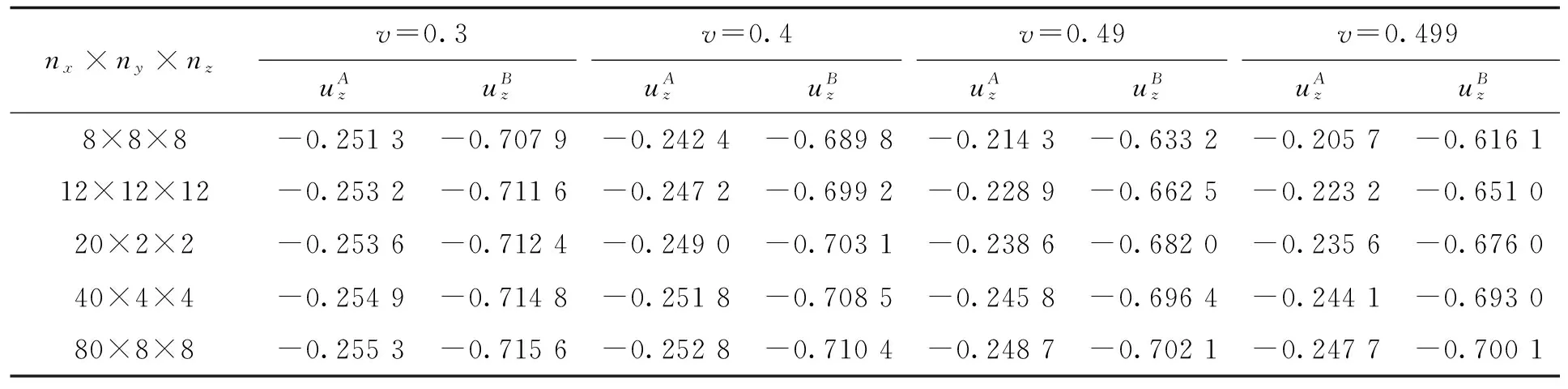
表2　悬臂梁轴线上A点和B点20节点二次元解Tab.2　The triquadratic element solutions of two typical points A and B on the cantilever axis

算例2(Cook膜问题)考虑如图2所示的三维Cook膜问题，其左侧面(即x=0)固定，右侧面上面力g=(0,0,t)T，其中，t=10N/mm2，弹性模量E=103N/mm2，不计自重。采用六面体网格进行剖分，分别采用8节点线三性元和20节点三二次元进行计算，相应的数值结果如表3和表4所示。

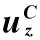
图2　三维Cook膜问题Fig.2　Three dimensional Cook’s membrane problems表3　结构网格下特征点C在z方向上的8节点线性元解Tab.3　The trilinear element solutions of on the structured meshes

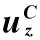
表4　结构网格下特征点C在z方向上的20节点二次元解Tab.4　The triquadratic element solutions of on the structured meshes

由上述数值结果可知：对于可压问题，随着网格规模的不断增加，特征点处的8节点线性元解均能收敛于理论解，而对近不可压缩问题，当ν→0.5时，8节点线性元解已不再收敛，20节点二次元解尽管收敛，但达不到最佳收敛结果，出现所谓的体积闭锁现象。另外，计算中所使用网格单元的质量也会影响计算结果的精度，如采用各向同性网格，则具有更好的计算精度。

克服这种闭锁现象的方法很多，如混合有限元法，非协调有限元法，高阶协调元法及减缩积分法等。对三维问题，常采用低阶非协调元(如二次元、线性元)来克服闭锁现象。这种方法具有自由度少、精度高的优点，可有效解决三维实际问题计算量过大的困难。

2　Wilson非协调元

六面体单元对应的位移模式不是完全多项式，而决定有限元解精度的是完全多项式的次数，非完全的高次项对改善精度不起作用，有时还可能会起相反的作用。Wilson非协调元通过在单元内部设置附加自由度，达到提高完全多项式的次数、改善计算精度的目的。这种单元的位移模式中包含了刚体位移和常量应变，但在相邻单元边界上不再保持连续性。笔者对如图3所示的局部坐标系o-ξηζ下的8节点和20节点六面体单元，分别建立Wilson非协调元计算格式。

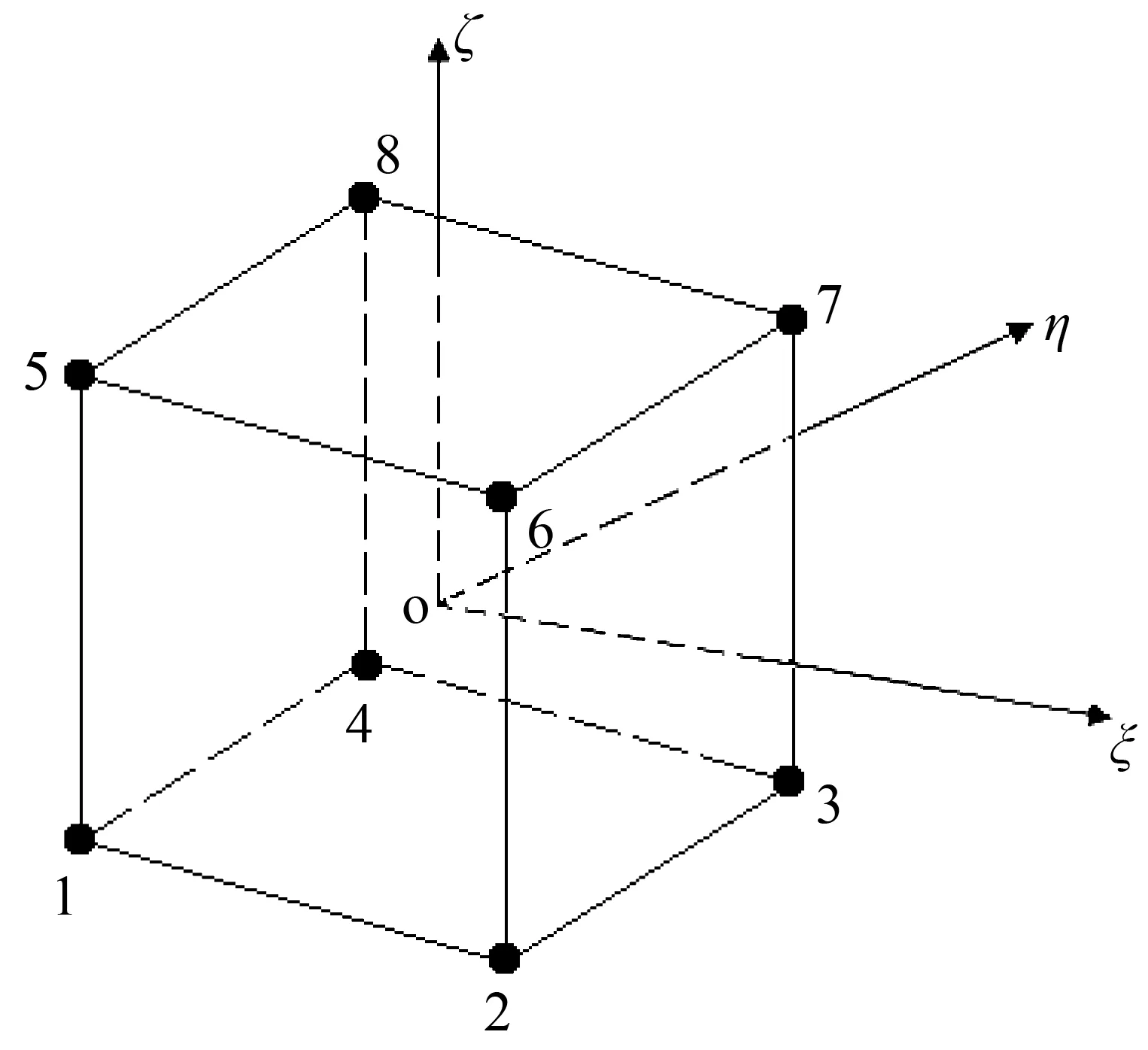
首先，设8节点六面体单元的非协调元位移模式为：

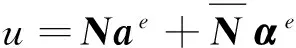
(6)

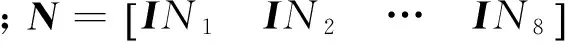
类似地，可得到20节点六面体单元形如式(6)所示的位移模式，其中：

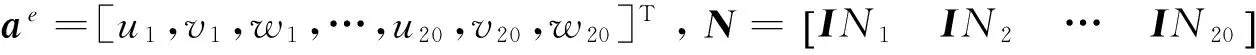
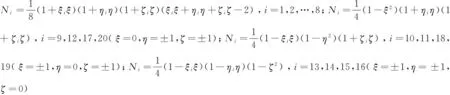
利用最小位能原理，可建立如下形式的单元刚度方程：

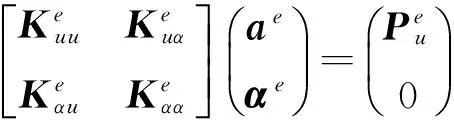
(7)

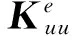
消去内部附加自由度αe，可得凝聚后的单元刚度方程为：

Keae=Pe,

(8)

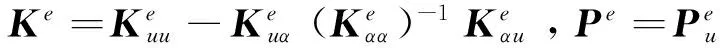
将上述8节点和20节点Wilson非协调元应用于两类近不可压缩问题：悬臂梁和Cook膜，以验证其有效性。

首先，对悬臂梁问题，当ν→0.5时，在不同网格规模和不同网格特性(各向同性网格和各向异性网格)下列出了悬臂梁轴线上A点和B点的两种Wilson非协调元解，总结如表5和表6所示。

表5悬臂梁轴线上A点和B点8节点Witson元解

Tab.5The 8-node Wilson element solutions of two typical pointsAandB

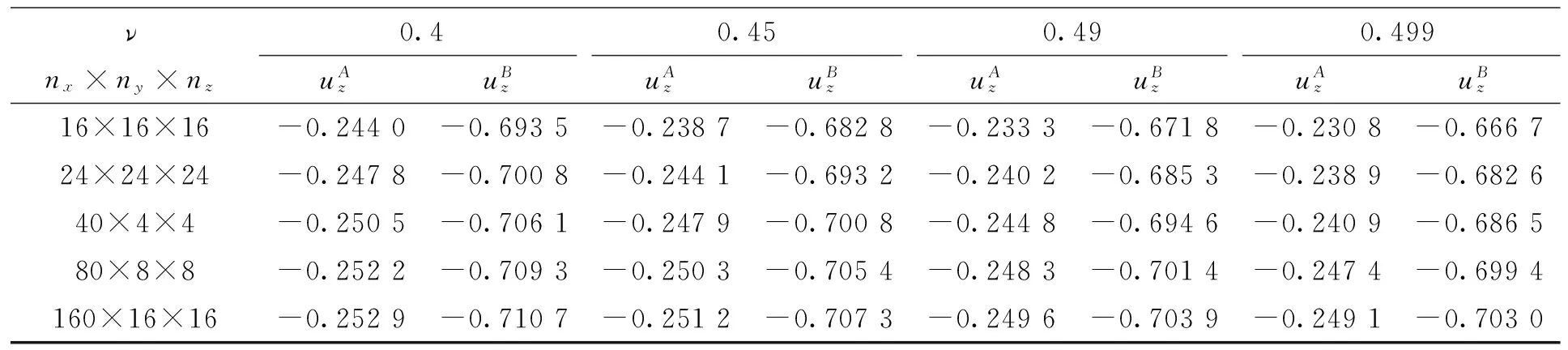
ν0.40.450.490.499nx×ny×nzuAzuBzuAzuBzuAzuBzuAzuBz16×16×16-0.2440-0.6935-0.2387-0.6828-0.2333-0.6718-0.2308-0.666724×24×24-0.2478-0.7008-0.2441-0.6932-0.2402-0.6853-0.2389-0.682640×4×4-0.2505-0.7061-0.2479-0.7008-0.2448-0.6946-0.2409-0.686580×8×8-0.2522-0.7093-0.2503-0.7054-0.2483-0.7014-0.2474-0.6994160×16×16-0.2529-0.7107-0.2512-0.7073-0.2496-0.7039-0.2491-0.7030

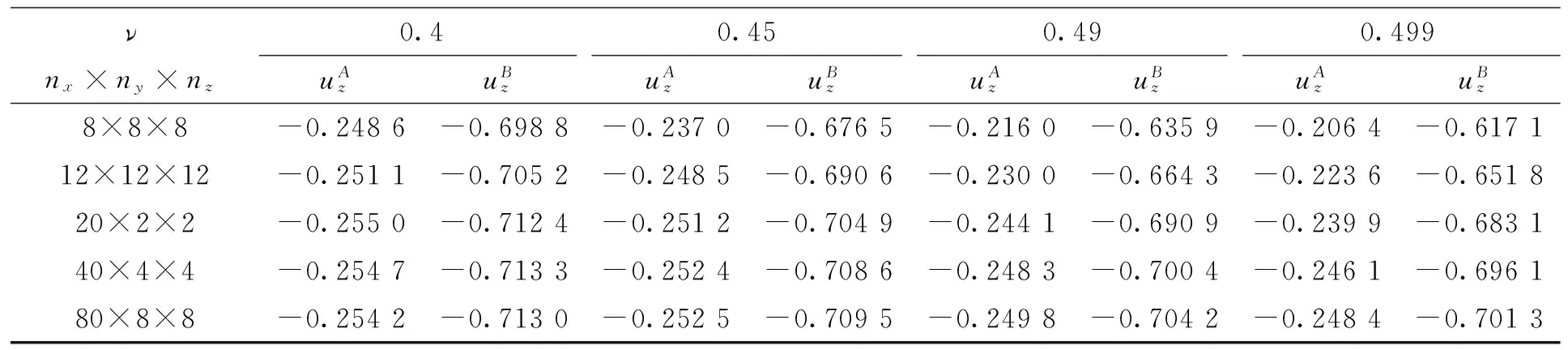
表6　悬臂梁轴线上A点和B点20节点Witson元解Tab.6　The 20-node Wilson element solutions of two typical points A and B

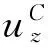
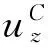
表7结构化网格下特征C在z方向上的8节点WILSON解

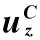
ν0.400.490.4950.4990.499516×16×163.954773.936903.932953.911783.9039124×24×243.977763.699743.967953.962543.957828×2×83.886813.829643.811363.725023.6493416×2×163.957153.941213.937593.922513.9083632×4×323.989303.985683.984773.982863.98116

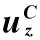
表8　结构化网格下特征点C在z方向上的20节点Wilson解Tab.8　The 20-node Wilson element solution of on the structured meshes

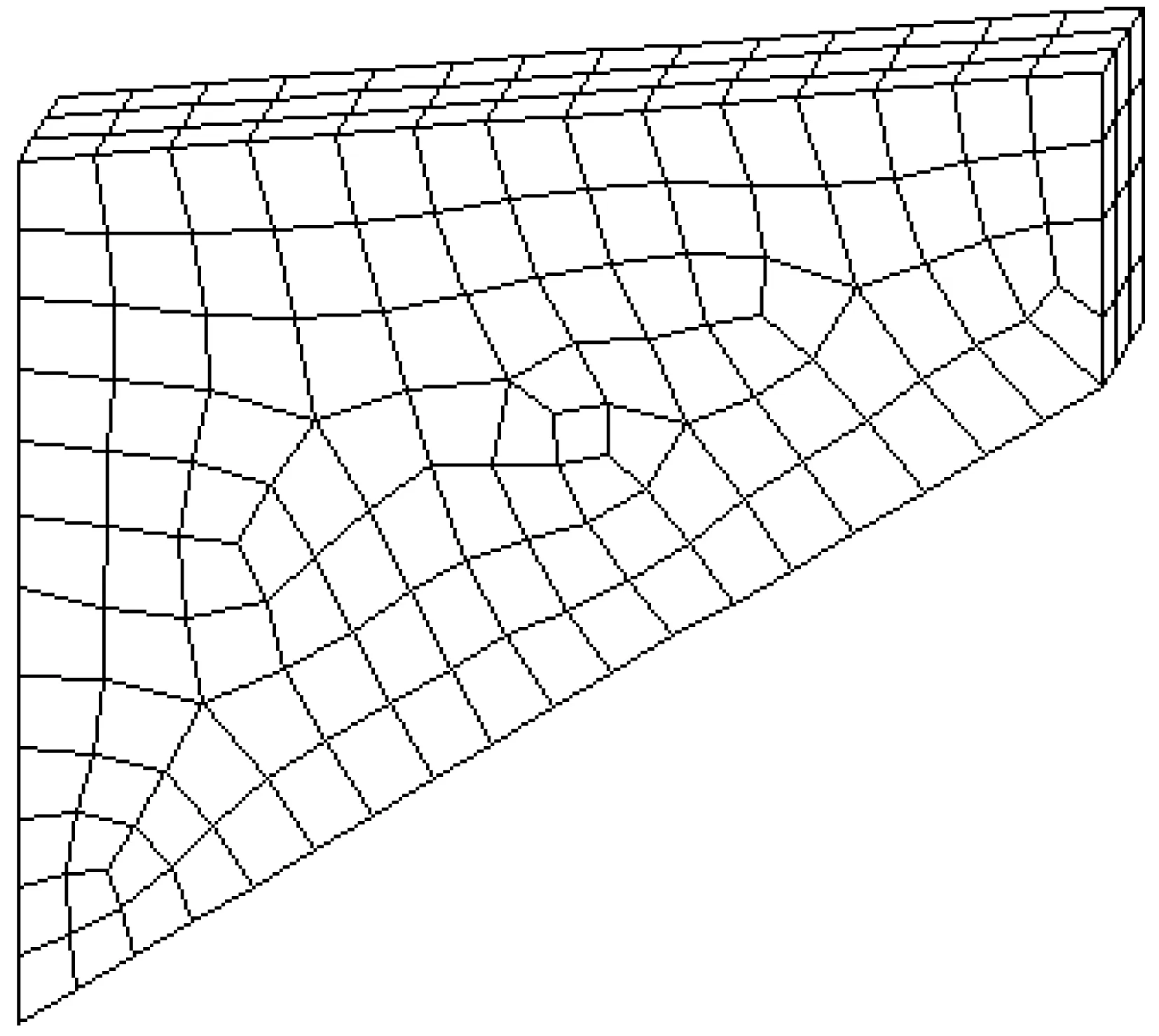
(a) 336个单元

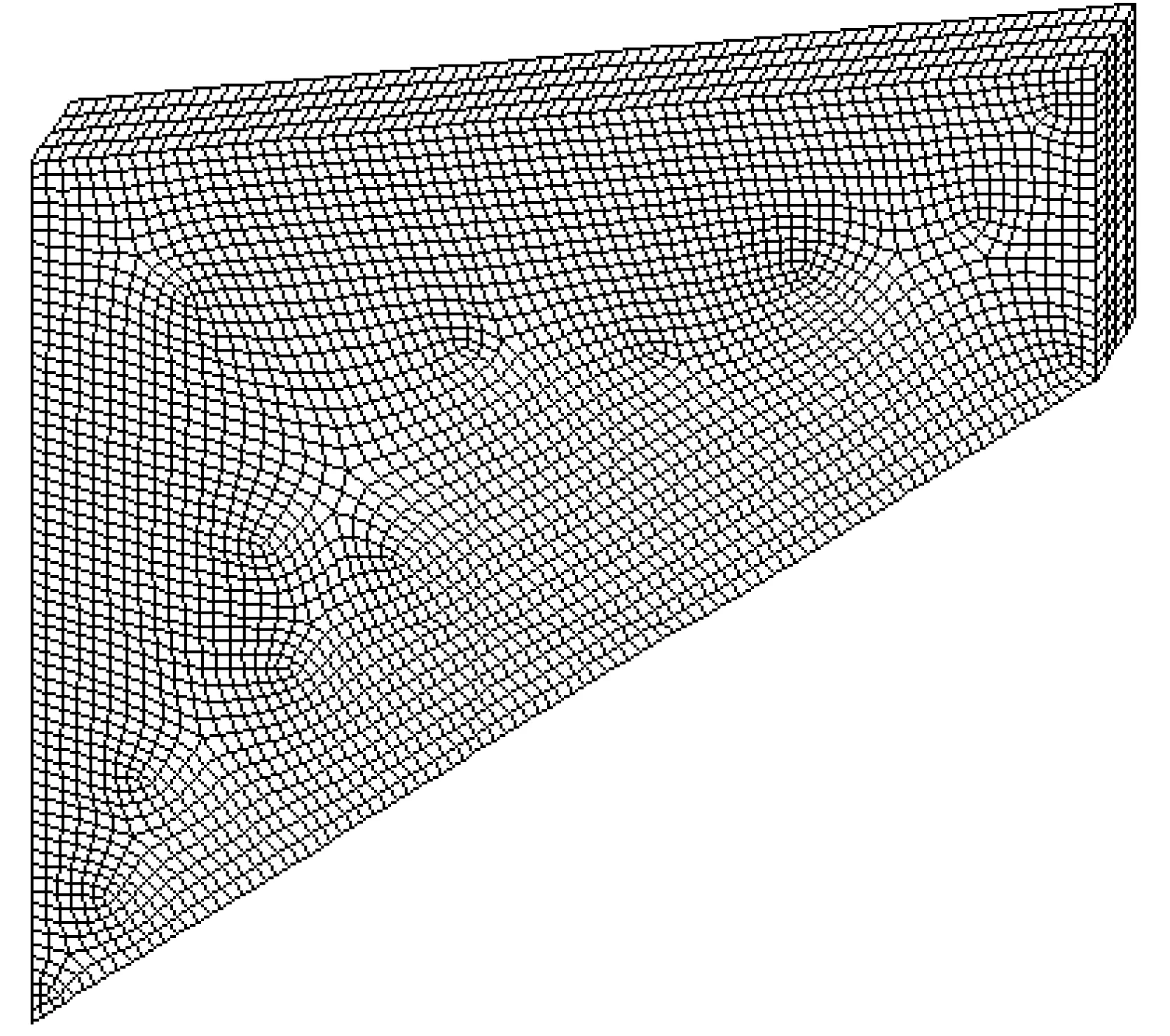
(b) 11 856个单元

图4三维Cook膜问题两种非结构化网格剖分

Fig.4Two unstructured meshes used for Cook’s membrane

表9非结构网格下特征C在z方向上的8节点Wilson解

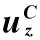
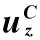
表10　非结构网格下特征C在z方向上的20节点Wilson解Tab.10　The 20-node Wilson element solution of on the structured meshes

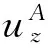
3　结　语

对三维近不可压问题，若利用通常的低阶协调元方法求解会出现所谓的体积闭锁现象。Wilson非协调元法是克服三维体积闭锁现象的一种有效方法，它具有自由度少、精度高的优点，可解决三维问题计算规模大的难题。Wilson非协调元对网格质量依赖性强，如何设计适用于任意六面体网格单元的低阶非协调元方法，将是我们进一步研究的问题之一。另外，针对这种非协调有限元分析中形成的大型的、稀疏的和高度病态的正定方程组，如何设计高效求解算法是一个非常困难的问题，将决定其有限元分析的整体效率，这也是我们今后将进一步研究的问题。

[1]CHEUNG Y K, CHEN W J.Hybrid element method for incompressible and nearly incompressible materials[J]. International Journal of Solids and Structures, 1989, 25(5): 483-495.

[2]MORLEY M.A mixed family of elements for linear elasticity[J]. Numerische Mathematik, 1989(55):633-666.

[3]CHAMA A, REDDY B D.New stable mixed finite element approximations for problems in linear elasticity[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 256: 211-223.

[4]WANG L H, QI H.A locking-free scheme of nonconforming rectangular finite element for the planar elasticity[J]. Journal of Computational Mathematics, 2004, 22: 641-650.

[5]FALK R S.Nonconforming finite element methods for the equations of linear elasticity[J]. Mathematics of Computation, 1991, 57: 529- 556.

[6]BRENNER S C.A nonconforming mixed multigrid method for the pure traction problem in planar linear elasticity[J]. Mathematics of Computation, 1994, 63: 435-460.

[7]SCOTT L R, VOGELIUS M.Conforming finite element methods for incompressible and nearly incompressible continua[C]//Large Scale Computations in Fluid Mechanics. Providence RI. American Mathematical Socity, USA: 1985, 22: 221-244.

[8]STENBERG R, SURI M.Mixed h-p finite element methods for problems in elasticity and Stokes flow[J]. Numerische Mathematik, 1996, 72: 367-390.

[9]HUGHES T J R.Equivalence of finite elements for nearly incompressible elasticity[J]. Journal of Applied Mechanics, 1977, 44: 181-183.

[10]MALKUS D S, HUGHES T J R.Mixed finite element methods-reduced and selective integration techniques: a unification of concepts[J]. Computer Methods in Applied Mechanics and Engineering, 1978, 15 (1): 63-81.

[11]QI H, WANG L H, ZHENG W Y.On locking-free finite element schemes for three dimensional elasticity[J]. Journal of Computational Mathematics, 2005, 23:101-112.

[12]鹿晓阳.Wilson 非协调元构造机理研究[J]. 工程力学，2000, 17(5): 58-62.

[13]张春生，龙驭球，须寅.三维内参型附加非协调位移基本项[J]. 工程力学，2000, 18(5): 58-62.

[14]陈震，林府标.三维Wilson元与特征值下界[J]. 南昌大学学报(理科版)，2010, 34(1): 19-23.

[15]王芬玲，石东伟，石东洋.拟线性Sobolev方程Wilson元解的超收敛分析及外推[J]. 工程数学学报，2012, 29(5): 720- 724.

(责任编辑唐汉民梁碧芬)

Wilson element and its application in nearly incompressible elasticity problems in three dimensions

LI Zhen-you, XIAO Ying-xiong

(Civil Engineering and Mechanics College, Xiangtan University, Xiangtan 411105, China)

In order to overcome the volume locking phenomenon of nearly incompressible problems in three dimensions, two types of Wilson nonconforming finite elements have been presented based on the hexahedral elements, and the resulting methods are then applied to the solution of two nearly incompressible problems with mixed boundary conditions.The numerical results have been shown that Wilson elements can effectively overcome the locking phenomenon, and it has higher accuracy compared with the conforming elements under the same mesh size.In three-dimensional finite element analysis, the quality of the mesh will have a great effect on the accuracy, and if the isotropic grids can be used in the practical calculations, the method will have better convergence.

nearly incompressible problem；volume locking；Wilson nonconforming element；mesh quality

2016-04-22；

2016-05-01

国家自然科学基金资助项目(10972191);湖南省自然科学基金资助项目(14JJ2063);湖南省教育厅资助科研项目(15A183)

肖映雄(1970—)，男，湖南城步人，湘潭大学教授；E-mail: xyx610xyx@xtu.edu.cn。

10.13624/j.cnki.issn.1001-7445.2016.1271

O343.2

A

1001-7445(2016)04-1271-08

引文格式：李真有,肖映雄.三维Wilson元及在近不可压弹性问题中的应用[J].广西大学学报(自然科学版)，2016，41(4)：1271-1278.