低周往复荷载作用下的空心桥墩抗震性能分析

申彦利，关　鹏,季春芳

(河北工程大学土木工程学院， 河北邯郸056038)



低周往复荷载作用下的空心桥墩抗震性能分析

申彦利，关鹏,季春芳

(河北工程大学土木工程学院， 河北邯郸056038)

为了研究不同因素对矩形空心桥墩抗震性能的影响，采用数值模拟方法，通过非线性静力分析，考察钢筋混凝土空心桥墩在低周往复荷载下的抗震性能。通过与已有试验数据比较，验证了数值模型的有效性及准确性。在此基础上研究轴压比、配箍率、配筋率、高宽比等因素对空心桥墩抗震性能的影响。结果表明，所建数值模型能够较好地模拟桥墩在低周往复荷载作用下的受力性能；在正常范围内稍稍提高轴压比可以提高桥墩的极限抗压承载能力；配筋率的提高也有利于桥墩的抗压承载能力的提升，而高宽比及配箍率的改变对桥墩的抗震性能影响不大。

低周往复荷载；空心桥墩；抗震性能；数值模拟

0　引　言

随着我国经济和社会的发展，高架桥梁的建设日趋普遍，尤其是在我国西南、西北等以山区居多的地区，山区的公路建设在地形复杂和陡峭的地方，很多桥梁都需要跨越河谷或者深沟，会采用到跨径不等的简支桥梁或者是大跨度的连续钢构桥，其桥墩高度往往会达到数十米甚至是上百米。我国属于地震频发的国家，地震所造成的损失是难以估量的。在交通系统中桥梁的作用是非常重要的，在发生地震时，主要是桥墩倒塌导致桥梁损毁，造成人员伤亡和财产的损失，所以，在桥梁抗震性能研究中，针对桥墩尤其是高墩的研究尤为重要。

Mander等[1]以空心矩形和圆形截面墩为研究对象，通过准静态实验研究其抗震性能。Pandey等[2]以15个钢筋混凝土空心桥墩为试验模型，分析比较了粘结纵筋桥墩和无粘结纵筋桥墩的破坏形式，发现无粘结纵筋混凝土的破坏形式为剪切破坏，而粘结纵筋桥墩的破坏形式为弯曲破坏；无粘结钢筋桥墩的刚度和耗能能力明显减小，屈服位移增加；两种桥墩的延性都随着配筋率增大而增大。杜修力等[3]以12个钢筋混凝土空心桥墩进行试验研究，结果表明，从承载力来看，矮墩的承载力最强，但是矮墩的刚度会退化得较快；配筋率可以明显提高桥墩的承载能力，轴压比大的桥墩承载力增加更明显。申彦利等[4]用OpenSees软件对空心桥墩在多维地震动作用下的抗震性能做了有限元分析。近几年，有关空心桥墩的试验研究有所增加，但针对试验的有限元模拟则不多见。为此，本研究从试验结果的有限元数值模拟出发，重点研究钢筋混凝土空心桥墩在低周往复荷载作用下的非线性静力响应，探讨不同因素对桥墩抗震性能的影响。

为了研究不同影响因素对空心桥墩的抗震性能的影响，本文采用有限元软件OpenSees进行数值建模，通过Pushover分析结果与试验数据的对比，验证了数值模型的有效性。在此基础上，对10个具有不同纵筋配筋率、轴压比、高宽比、体积配箍率的模型进行非线性静力分析，以探究不同结构特性参数对桥墩在低周往复荷载下抗震性能的影响。

1　桥墩数值模型

1.1基本参数

本研究基于北京工业大学空心桥墩试验的数据[6]及《桥梁相关抗震设计细则》(JTG/TB02-01-2008)[7]，建立2个墩高分别为2 880 mm及3 600 mm的矩形空心桥墩模型，外廓尺寸为500 mm×360 mm，空心尺寸为260 mm×120 mm，见图1。墩身混凝土等级选用C40，纵筋直径为8 mm，箍筋直径为6 mm，均为Ⅱ级钢筋，混凝土材料和钢筋材料的力学性能见表1，表2。

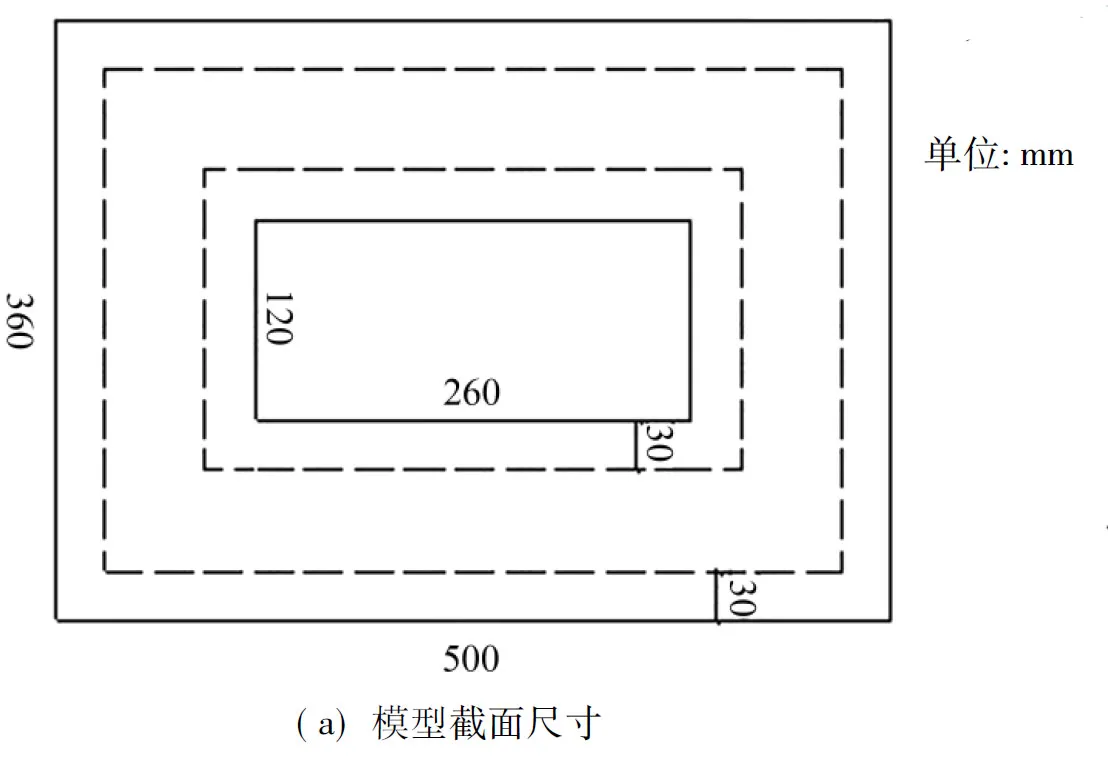
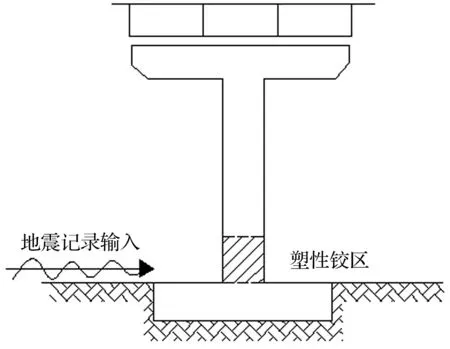
表2　钢筋材料力学性能Tab.2　Material Properties of Reinforcement

1.2基本假定

本研究采用OpenSees软件对模型进行数值分析[8-9]，为保证计算模型符合结构实际受力情况，选取了《桥梁抗震细则》(JTG/TB02-01-2008)[7]中对计算模型的相关假定： ①墩柱采用顶部质量集中的悬臂杆模拟；②桥墩为等截面，墩底设置塑性铰； ③不考虑桥面对桥墩的纵向约束作用，忽略支座与梁体的刚度耦合作用； ④不考虑基础或地基对结构的约束作用，采用刚性约束模式，计算结果偏安全。

1.3材料模型

在纤维截面模型中，OpenSees程序需对材料本构关系进行识别，使其具有实际材料的受力性能。混凝土本构关系滞回模型取自修正后的Kent-Park模型[10-12]，这类材料考虑了混凝土的残余强度及线性拉伸软化。混凝土滞回模型见图2。

钢筋本构关系滞回模型的选取对于往复荷载下的滞回曲线影响较大，合理选择钢筋受力机制是保证数值分析准确性的关键。实际试验中，纵筋的受力状态包括拉压屈服，甚至是被拉断，从而导致结构承载力完全丧失，与此同时，还存在明显的强度和刚度退化。本研究中所采用的模型是基于Chang等[13]提出的各向同性硬化钢筋模型，其骨架曲线可以通过简单的拉伸试验得到。这个材料模型考虑了钢筋的屈曲、低周循环时钢筋的强度和刚度退化情况，材料退化行为模拟主要依据以下两个参数：一个是Cf疲劳延性系数，其值控制循环加载次数，其值越大，钢筋断裂前能够承受的加载次数越多；另一个是Cd疲劳强度退化系数，其值控制循环加载导致的钢筋强度退化量，其值越大，强度退化越小。钢筋滞回模型见图3。

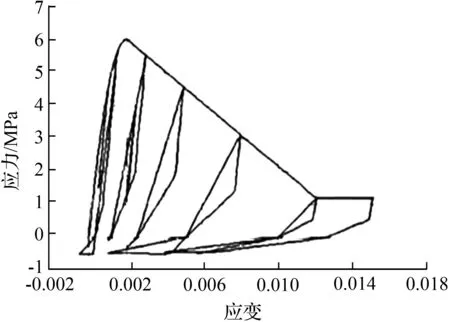
图2混凝土滞回模型

Fig.2Concrete hysteretic model

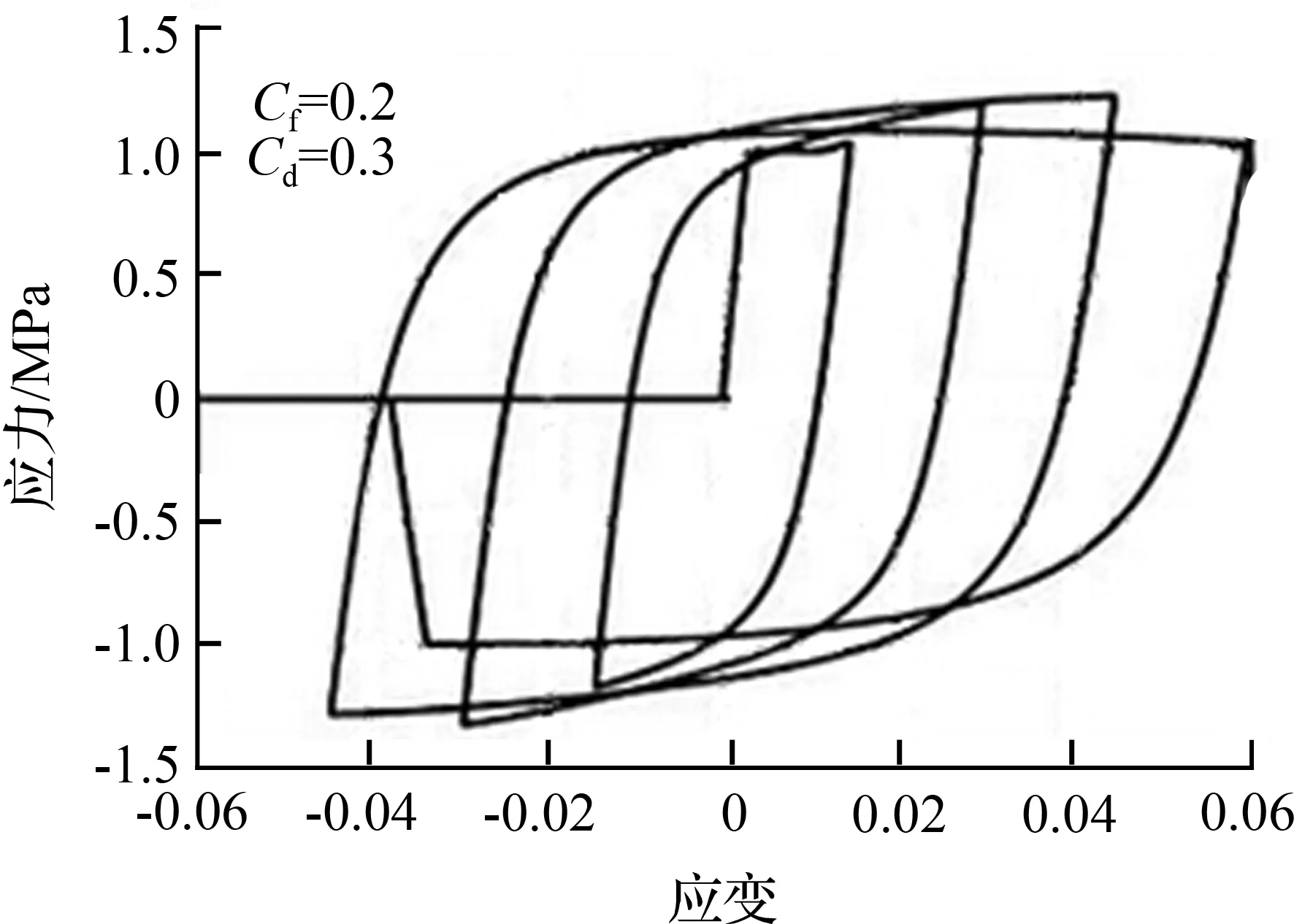
图3钢筋滞回模型

Fig.3Steel hysteretic model

1.4截面和单元模型

桥墩截面用纤维单元来划分，如图4(a)所示。将混凝土划分成矩形单元和钢筋分层，以便使弹塑性计算分析更加精确细致，使分析结果比较符合实际受力情况。

对于沿顺桥向的单自由度悬臂墩模型，其最大剪力及弯矩常出现在桥墩底部，因此，常将桥墩底部定义为塑性铰区域。当考虑地震作用时，等截面桥墩的塑性铰需设置在桥墩底部位置。桥墩非线性响应考虑构件延性，墩底设置了塑性铰区，见图4(b)。其中，高2 880 mm的桥墩塑性铰长度设置为340 mm，高3 600 mm桥墩塑性铰长度设置为398 mm。对单墩的模拟采用梁铰单元，上部为线弹性单元，底部为塑性铰单元，主要模拟桥墩的非线性响应，包括基底剪力、钢筋粘结—滑移等。材料本构关系设置在截面纤维条上[10-12]。

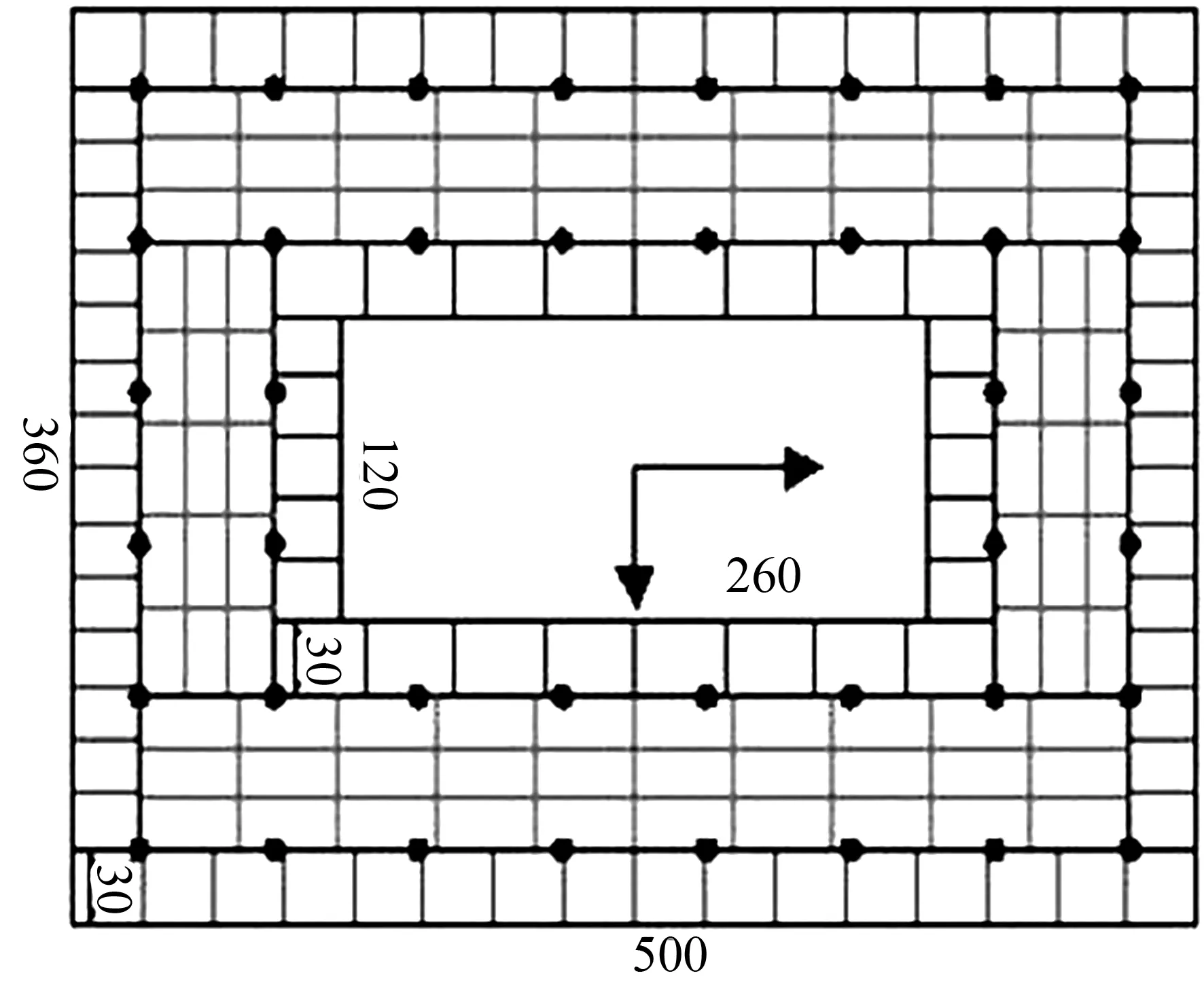
(a) 截面单元划分单位：mm

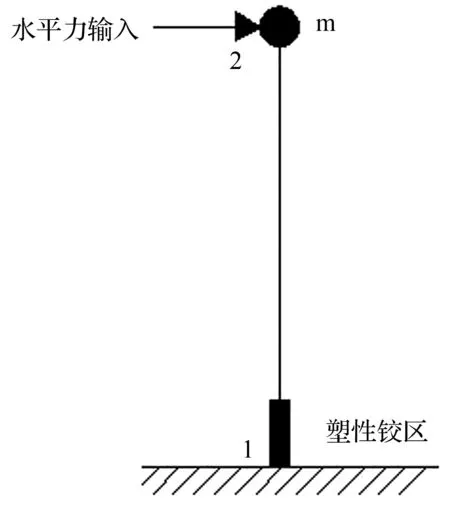
(b) 塑性铰区示意图

图4桥墩分析模型

Fig.4Piers analysis model

1.5边界条件及加载方式

本研究对不同墩高的2个空心桥墩模型进行非线性Push-over分析，其结构简化为空间悬臂杆件，计算体系为单自由度体系，结构响应模式以第一振型为主，截面形式保持不变。计算时，在模型自由端施加280 kN恒定竖向约束，采用位移增量控制加载，最大推覆侧移取0.05倍柱高，水平位移增量取0.000 01倍柱高，每个模型的分析步长为5 000步。

2　数值模拟的正确性验证

对已建好的数值模型进行静力加载分析[14-16]，可以得到模型在不同加载阶段的力—位移曲线。图5、图6所示分别为桥墩高2 880 mm和3 600 mm的力—位移曲线图模拟结果与试验结果。数值模拟结果与试验结果见表3、表4。

以墩高2 880 mm的桥墩为例，试验得到的屈服荷载Py为63.89 kN，数值模拟的屈服荷载Py为68.70 kN，误差7.1%；试验得到的屈服位移Uy为40.71 mm，数值模拟的屈服位移Uy为35.82 mm，误差达13.6%。从墩高3 600 mm的桥墩数值模拟结果与试验结果的对比可以看出，试验得到的屈服荷载Py为86.30 kN，数值模拟的屈服荷载Py为92.33 kN，误差率为6.5%；试验得到的屈服位移Uy为60.10 mm，数值模拟屈服位移Uy为55.09 mm，误差率为9.1%。两种墩高的最大荷载及最大位移的数值模拟与试验结果见表4。

从图5、图6可以看出，无论是高墩还是矮墩，从数值模拟的结果看，其屈服荷载、屈服位移、最大荷载以及最大位移都要偏高于试验数据，但其偏差数值都是在容许范围内。通过对比数值模拟和试验结果的两种力—位移曲线可以看出，所建有限元模型能够较好地模拟试验结果。

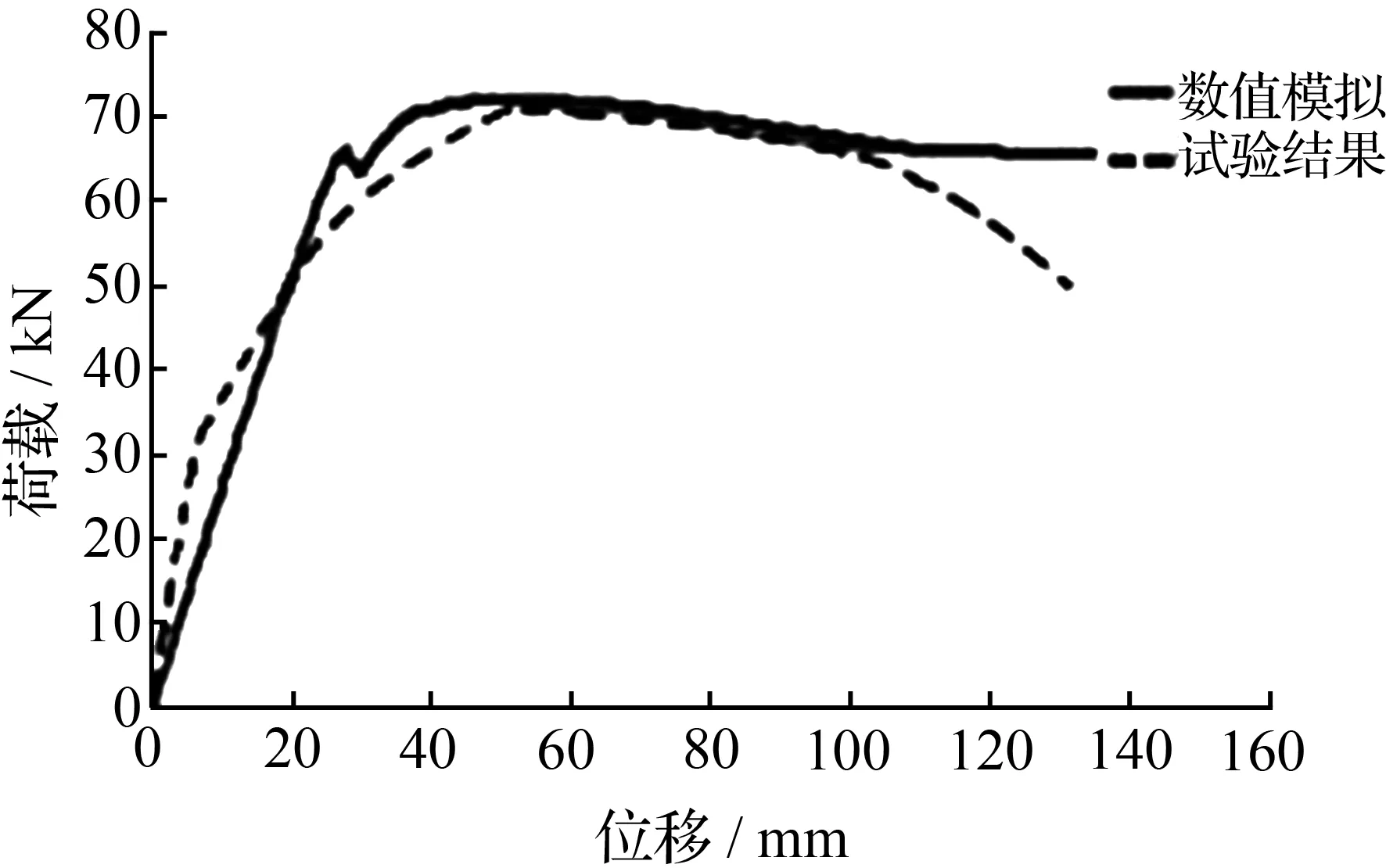
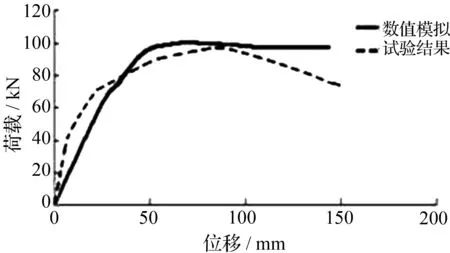
图5　2 880 mm墩高力—位移曲线Fig.5　Force and displacement curve of 2 880 mm high pier

表4　最大荷载与最大位移对比数据Tab.4　The maximum load and maximum displacement data comparison

3　影响参数的分析

矩形空心桥墩的抗震性能受多种因素影响。 为了进一步探究配筋率、轴压比、高宽比以及配箍率等不同因素对矩形空心桥墩抗震性能的影响，建立10个具有不同高宽比、轴压比、配筋率以及配箍率的钢筋混凝土矩形空心桥墩。其具体模型参数见表5。

在分析不同因素对桥墩抗震性能的影响时，本研究对以上模型采用低周往复循环加载方式，将得到的每次循环加载达到的水平力最大峰值的点相连所形成的轨迹则是骨架曲线，该曲线反映了构件受力与变形的各个不同阶段及特性(强度、刚度、延性、耗能及抗倒塌能力等)，通过分析所得骨架曲线来探究这些变量对桥墩抗震性能的影响。

3.1纵筋配筋率对桥墩抗震性能的影响

本研究主要对不同墩高的空心桥墩做非线性静力分析，通过绘制力位移骨架曲线来分析桥墩的抗震性能。图7和图8分别为不同墩高的柱子在纵向钢筋配筋率不同时的骨架曲线。可以看出，配筋率的改变对模型S1、S2和S6、S7的作用比较明显，但对S3、S4和S8、S9的作用并不明显。

由图7与图8可以看出，配筋率的提高对试件的承载力有一定的提高作用。在轴压比一定的情况下，提高配筋率的4组对比试件的屈服承载力分别提高4.1%、90.1%、0.4%、15.2%，对应的极限承载力则分别提高3.5%、86.2%、1.5%、11.5%。由此可以看出，较高配筋率与在正常范围内稍微增加的轴压比共同作用对试件的承载力影响较大，同时配筋率对试件早期的影响较大。

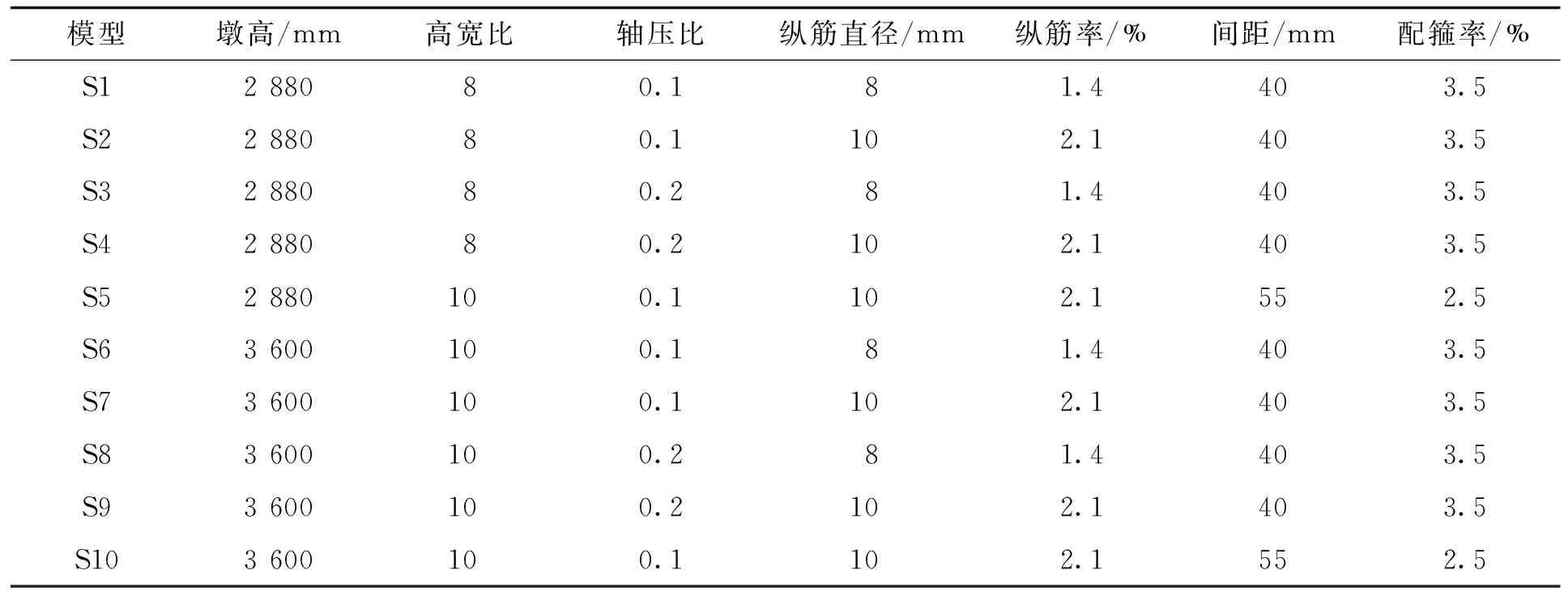
表5　模型设计参数Tab.5　Model design parameters

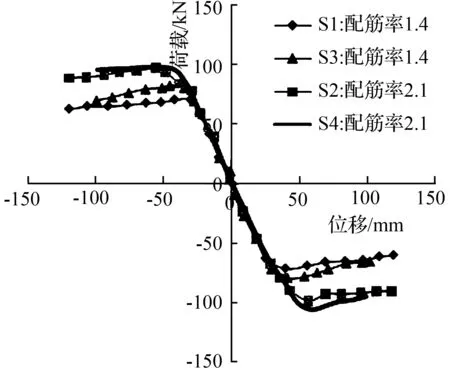
图72 880 mm墩高不同配筋率下的骨架曲线图

Fig.7Different reinforcement ratio skeleton curves of 2 880 mm high pier

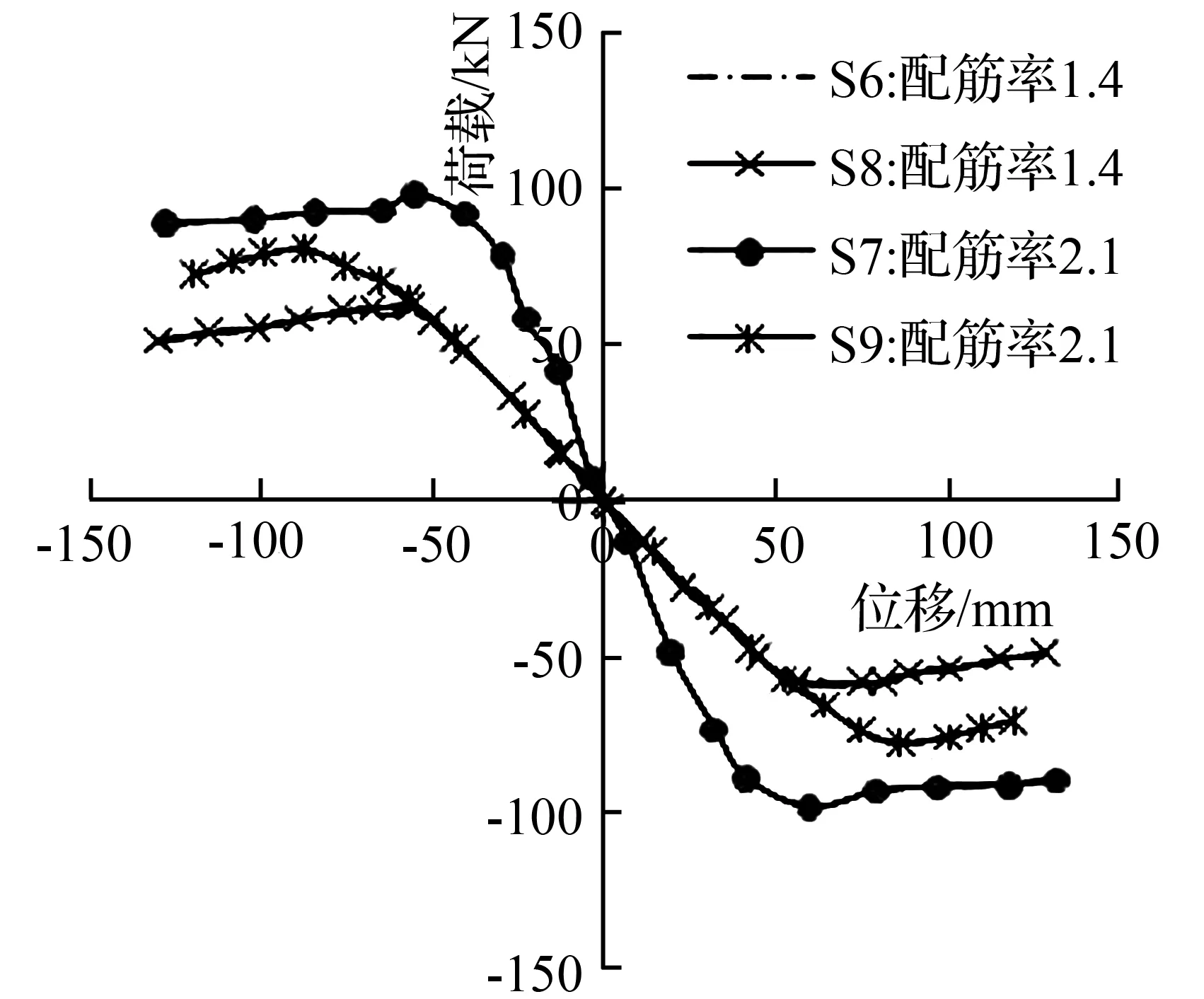
图83 600 mm墩高不同配筋率下的骨架曲线图

Fig.8Different reinforcement ratio skeleton curves of 3 600 mm high pier

3.2轴压比对桥墩抗震性能的影响

轴压比是反映构件延性性能和受压性能的一个重要指标，定义为：

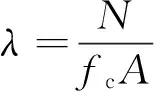
(1)

式中，N为轴压力，fc为混凝土轴向抗压强度，A为顶部面积。

图9和图10分别是墩高2 880 mm桥墩以及墩高3 600 mm桥墩在不同轴压比时的骨架曲线。从图9和图10可以看出，轴压比大小对不同墩高两试件的骨架曲线影响趋势一致，轴压比的变化对墩高2 880 mm桥墩的影响要大于墩高3 600 mm桥墩的。

之所以出现这种情况，是因为随着试件高度增加，轴向力对试件的约束减弱，同时，在桥墩较高的情况下，在较大轴压力的作用下，桥墩中部容易发生弯曲，从而影响其受力性能。两种高度的试件，轴压比相对大的试件其承载力都有较大提升。相较于S1模型， S3模型的屈服荷载及极限荷载分别提高49.2%和53.6%。而相较于S6模型，S8模型的屈服荷载和极限荷载分别提高9.1%和19.82%。

图92 880 mm墩高不同轴压比下的骨架曲线图

Fig.9The skeleton curve with different coaxial pressure of 2 880 mm high pier

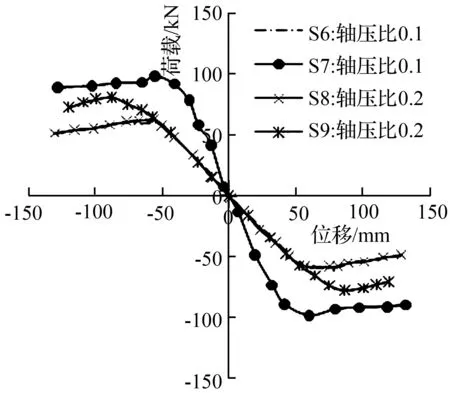
图103 600 mm墩高不同轴压比下的骨架曲线图

Fig.10The skeleton curve with different coaxial pressure of 3 600 mm high pier

3.3高宽比对桥墩抗震性能的影响

为研究高宽比对桥墩抗震性能的影响，分别建立了4组模型，控制其他参数不变并进行两两对比。图11是在配筋率为1.4的两个模型的骨架曲线对比图。从图11中不难看出，S1的骨架曲线要略高于S6的。图12是在配筋率为2.1的两个模型的骨架曲线对比图，与图11不同的是，这两个曲线重合在一起。

纵筋含量小时，高宽比的变化对构件的刚度影响较大，同时，当纵筋含量相对较高时，其对构件的整体刚度影响较小，反而对构件的截面刚度影响较大。

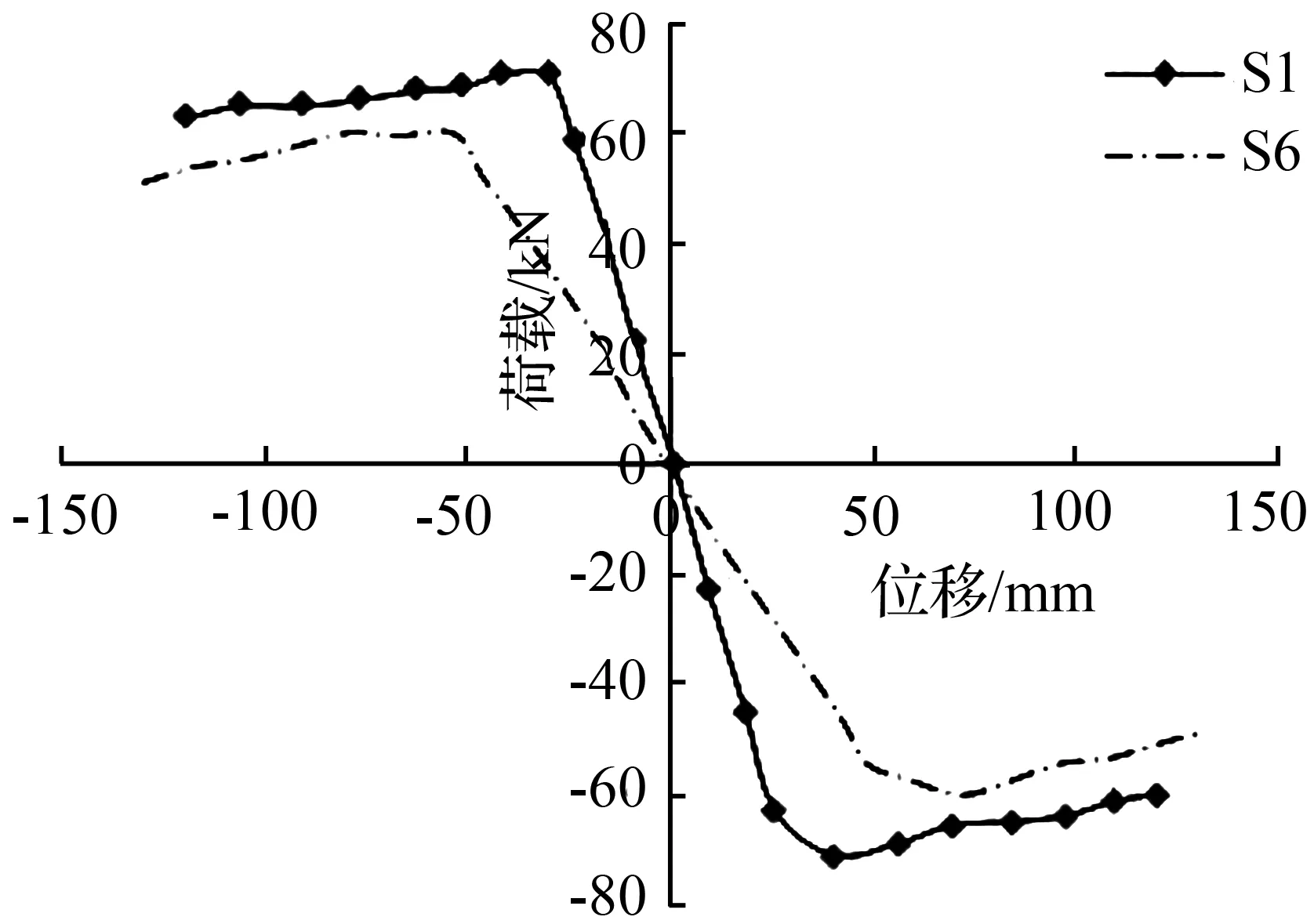
图11不同高宽比桥墩的骨架曲线图

Fig.11The skeleton curve with different height to width ratio of pier

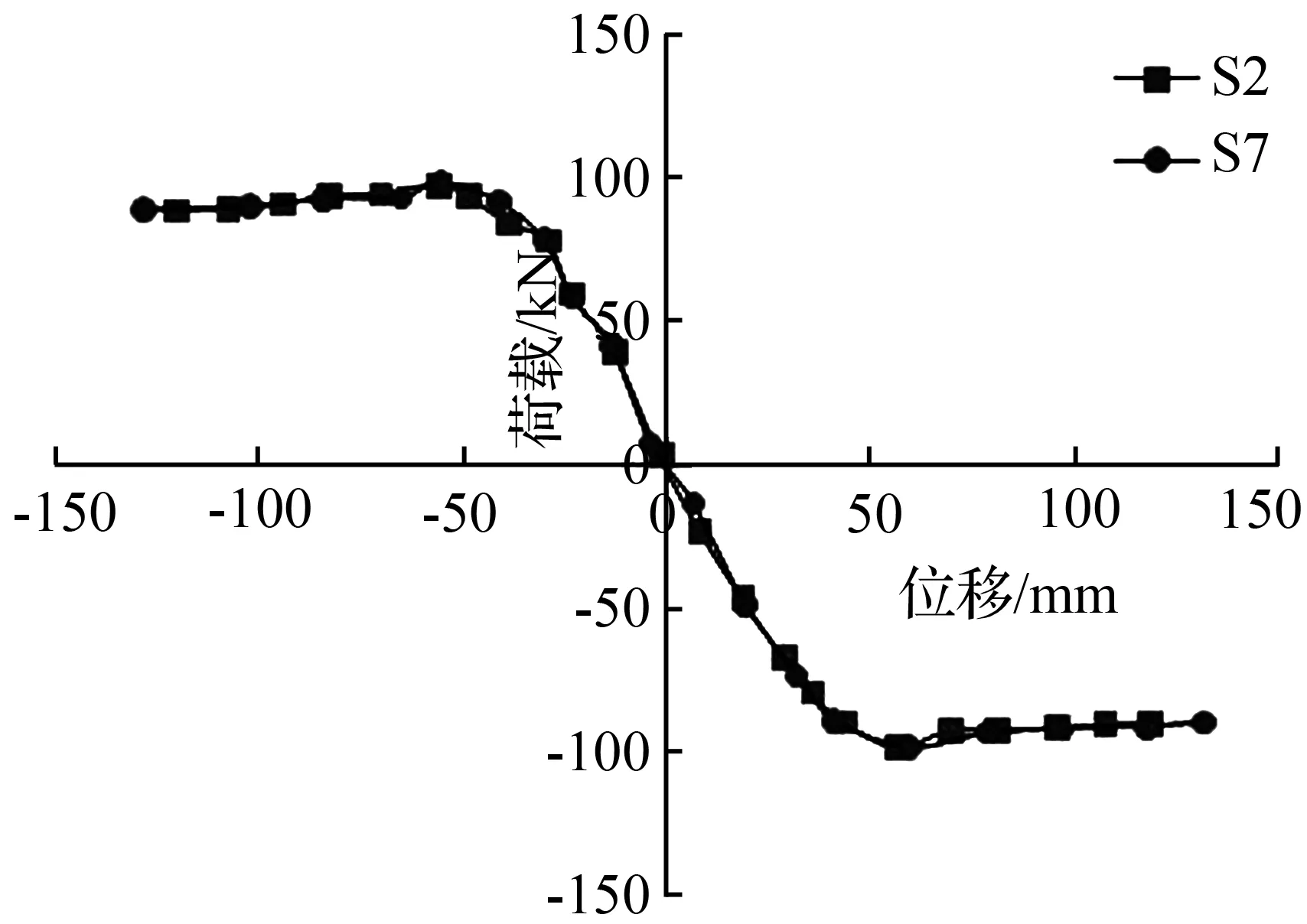
图12不同高宽比桥墩的骨架曲线图

Fig.12The skeleton curve with different height to width ratio of pier

3.4配箍率对桥墩抗震性能的影响

为研究配箍率对桥墩骨架曲线的影响，设计了0.35和0.25两种配筋率模型，其骨架曲线如图13、图14所示。从图13和图14可以看出，无论是2 880 mm墩高的模型还是3 600 mm墩高的模型，两种配筋率模型的骨架曲线基本重叠。

虽然配箍率不同，但是试件的承载力变化并不明显，也就是说，配箍率对矩形空心桥墩中的影响并不显著。

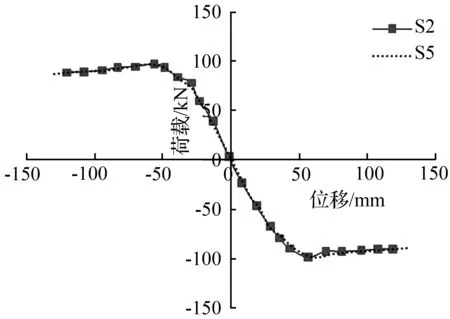
图13不同配箍率桥墩的骨架曲线

Fig.13The skeleton curve with different stirrup ratio of pier

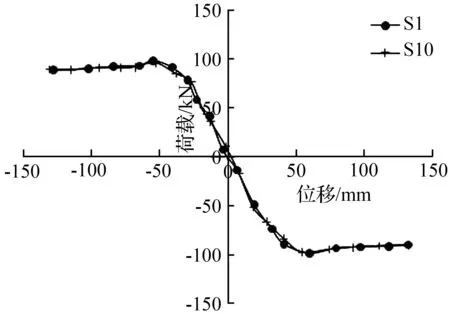
图14不同配箍率桥墩的骨架曲线

Fig.14The skeleton curve with different stirrup ratio of pier

4　结　语

本研究利用 OpenSees 中的梁铰纤维单元建立10个钢筋混凝土空心桥墩数值模型，进行了非线性静力分析，通过比较模拟结果与试验结果来验证数值模型的有效性，并在此基础上进一步研究不同因素对桥墩抗震性能的影响，得到如下主要结论:

①本研究采用Chang等提出的各向同性硬化钢筋本构关系模型对桥墩的骨架曲线有良好的模拟效果。

②从10个桥墩的模拟结果来看，轴压比和配筋率对桥墩的抗震性能影响较大，无论是高墩还是中墩，在高轴压比为0.2、配筋率为2.1时，其极限承载力提高幅度分别为86.2%，90.1%。高宽比以及配箍率对试件抗震性能的影响微乎其微。

本研究不足之处在于骨架曲线无法反应桥墩的耗能能力。这有待下一步研究桥墩的滞回曲线，以便全面分析桥墩的抗震性能。

[1]MANDER J B .Seismic design of bridge piers[D]. New Zealand：The University of Canterbury,1983.

[2]PANDEY G R, MUTSUYOSHI H.Seismic performance of reinforced concrete piers with bond-controlled reinforcements.[J]Suctural Journal,2005,102(2):295-304.

[3]杜修力,陈明琦,韩强.钢筋混凝土空心桥墩抗震性能试验研究[J]. 振动与冲击，2011，30(11)：254-259.

[4]申彦利,赵雪.钢筋混凝土空心桥墩抗震性能分析[J]. 广西大学学报(自然科学版),2014,39(1)：48-53.

[5]凌炯.面向对象开放程序OpenSees在钢筋混凝土结构非线性分析中的应用与初步开发[D]. 重庆：重庆大学，2004.

[6]陈明琦.钢筋混凝土空心桥墩抗震性能试验研究[D]. 北京：北京工业大学，2011.

[7]中华人民共和国交通运输部.JTG/T B02-01-2008 公路桥梁抗震设计细则[S]. 北京：人民交通出版社，2008.

[8]KOWALSKY M J.Deformation limitstates of circular reinforced concrete bridge columns[J]. Journal of Structural Engineering, 2000, 126(8): 869-878.

[9]王建民，朱晞.圆截面RC桥墩曲率极限状态和延性的概率分析[J]. 土木工程学报，2006, 39(12): 88-94.

[10]KENT D C, PARK R.Flexural members with confined concrete[J]. Journal of the Struetural Division, 1971, 97(7): 1969-1990.

[11]MAZZONI S, MCKENNA F, FENVES G L.OpenSees command language manual[Z]. Berkeley: University of California, 2007.

[12]李贵乾，郑罡，高波.基于OpenSees的钢筋混凝土桥墩拟静力试验数值分析[J]. 世界地震工程，2011, 27(1): 110-114.

[13]CHANG G A, MANDER J B. Seismic Energy Based FatigueDamage Analysis of Bridge Columns Part I-Evaluation of Seismic Capacity[R]. New York: State University of New York, 1994.

[14]邓江东，郑茂金.OpenSEES在混凝土桥墩滞回性能分析中的应用[J]. 福建建筑，2011, 157(7): 99-102.

[15]汪大绥，贺军利，张凤新.静力弹塑性分析(Pushover Analysis)的基本原理和计算实例[J]. 世界地震工 程，2004, 20(1): 45-53.

[16]ANIL K, RAKESH K.Capacity-demand-diagram methods for estimating deformation of inelasticstructures SDF systems[R]. Berkeley:University of California, 2002-03-27.

(责任编辑唐汉民裴润梅)

Study on seismic performance of hollow pier under low cyclic reversed loading

SHEN Yan-li, GUAN Peng, JI Chun-fang

(School of Civil Engineering, Hebei University of Engineering, Handan 056038, China)

In order to study the influence of different factors, such as axial compression ratio, reinforcement ratio, the ratio of height to width, on the seismic performance of rectangular hollow bridge piers, the seismic behavior of reinforced concrete hollow bridge piers under low cyclic reversed loading is investigated by a numerical simulation. The validity and the accuracy of the finite element model were verified by comparing the simulation results with the experimental data. The analysis results show that the numerical model can simulate the mechanical behavior of piers under low cyclic reversed loading. The ultimate compressive capacity of bridge piers can be improved with higher axial compression ratio. The higher reinforcement ratio can also improve the ultimate compressive capacity of bridge piers. However, the change of height to width ratio and stirrup ratio has little effect on the seismic performance of the bridge piers.

low cyclic reversed loading；hollow pier；seismic performance；numerical simulation

2016-01-10；

2016-05-28

国家自然科学基金资助项目(51378169)；河北省自然科学基金资助项目(E2013402072)

申彦利(1956—)，男，河北邯郸人，河北工程大学副教授，博士；E-mail：shenyanli@hebeu.edu.cn。

10.13624/j.cnki.issn.1001-7445.2016.1255

U442.5

A

1001-7445(2016)04-1255-09

引文格式：申彦利，关鹏,季春芳.低周往复荷载作用下的空心桥墩抗震性能分析[J].广西大学学报(自然科学版)，2016，41(4)：1255-1263.