纯铜中心孔板拉伸断裂的实验研究
2016-08-30蔡德良秦胜欢刘贵龙张克实
蔡德良,秦胜欢,高 柳,刘贵龙,张克实
(广西大学土木建筑工程学院, 工程防灾与结构安全教育部重点实验室, 广西南宁530004)
纯铜中心孔板拉伸断裂的实验研究
蔡德良,秦胜欢,高柳,刘贵龙,张克实
(广西大学土木建筑工程学院, 工程防灾与结构安全教育部重点实验室, 广西南宁530004)
为了测试材料在应力三轴度接近1/3时的断裂应变,对9种不同厚度不同孔径的T2纯铜中心孔板试样,在MTS试验机上进行系列拉伸试验。结合数值模拟和显微观测,确定孔板试样的裂纹萌生位置及其应力三轴度数值及断裂应变。在此基础上,参照比较光滑试样拉伸试验,进一步探讨了对材料应力三轴状态与断裂应变的关系。研究发现:①材料断裂应变随应力三轴度减少而减少,似不服从以往基于孔洞模型研究总结出来的韧性材料断裂规律;②孔表面实际变形很不均匀,按连续介质力学方法估计的孔边断裂应变要明显低于其实际值。
T2纯铜;大应变拉伸;数值模拟;应力三轴度;断裂应变
很早人们就发现韧性材料的断裂与三轴应力作用下材料中微孔洞的形核、长大和聚合有关。McClintock[1]、 Rice等[2]分别通过研究长柱孔洞和球形孔洞的成长过程,试图用含微孔洞材料的体胞模型分析来解释材料的韧性断裂机理,并发现相同等效应变情形下远场应力三轴度越大则微孔洞长得越大。由于微孔洞长大与孔洞周围局部应变有关,因此得出较大的应力三轴度导致较小的断裂应变的结论。这里应力三轴度Rσ的定义为:

(1)

Bao等[16]用金属2024-T351铝板进行了一系列试验研究,得到了涵盖从压缩应力状态到三轴拉伸应力状态范围的等效断裂应变和应力三轴度的关系(应力三轴度从-1/3到0.95)。该结果表明,在应力三轴度大于零的范围内,最大断裂应变是在光滑圆棒单轴拉伸时达到的,此时应力三轴度约为0.4。而应力三轴度在大于等于0但小于0.4的区间和大于0.4的区间,断裂应变随应力三轴度变化有所不同。在前者区间内是单调增加,在后者区间内是单调减小。但李柳等[12]对T2纯铜平板斜缺口拉伸剪切试验的结果表明,在应力三轴度远低于单轴拉伸颈缩断裂发生时光滑圆棒试样颈部应力三轴度(约0.63)的情形,拉伸剪切试验断裂应变与光滑圆棒拉伸断裂应变相当,并无明显下降。因此,Bao等的结果不一定具有普遍性,而且他们的研究对一些试样的应力状态和断裂应变的定义位置没有给出清楚说明,其结论还有待进一步认识。
本研究将对9种不同孔径不同厚度的纯铜中心圆孔板试样进行单轴拉伸试验(这种试样破坏区域在变形过程中应力三轴度始终约为1/3),用有限元方法计算试样的应力应变场。结合试验与数值模拟,确定孔板试样的起裂位置、该处应力三轴度数值以及断裂应变。在此基础上,对材料应力三轴状态与断裂应变的关系开展更进一步的研究,旨在找出金属材料的应力三轴度与断裂应变关系准则。
1 拉伸试验与模拟
1.1材料与试验设备
采用T2纯铜棒材(直径26 mm)进行试验,其化学成分见表1,力学性能见表2。加工试样前将材料在高温电炉中加热到620 ℃保温1 h,然后采用自然冷却进行退火处理(属于再结晶退火)。采用线切割加工试样,然后进行表面抛光。试样尺寸见图1。试样按孔径d和厚度t的尺寸编号,形式为“dmtn”,m和n是尺寸(单位为mm,例如,d3t4表示d=3 mm,t=4 mm),相应的韧带宽i=0.5w(试样宽)-0.5d(孔径)。试样开圆孔后,拉伸试验时试样破坏将从孔边开始。因为开孔板试样韧带颈缩很少,而且孔边位于自由表面,该处变形过程中近似为单轴应力状态,其应力三轴度保持接近于1/3。
试验在室温下采用MTS809材料拉扭试验机上进行,试验机最大静载荷为250 kN。所有试验用位移控制加载方式加载,加载速率为0.02 mm/s。引伸计轴向标距为25 mm,其最大应变量程为20%。

表1 工业纯铜(T2)的化学成分(质量分数)Tab.1 Chemical composition of commercially pure copper-T2 (mass fraction) %

表2 纯铜(T2)的力学性能Tab.2 Mechanical properties of pure copper-T2

图1孔板试样几何尺寸(w=20 mm)
Fig.1Specimen geometry and size
1.2拉伸试验结果与分析
对各试样实测的位移—荷载曲线进行处理,得到相同孔径下的单位面积位移—载荷曲线,如图2所示,曲线终点为试样起裂点(即孔边表面出现深度≥1 mm裂纹的时刻)。由图2可知,对相同孔径而厚度不同的试样,其单位面积载荷峰值和名义断裂应变的差异都不大,其均值的最大偏离<4%。该结果表明厚度增加对名义断裂应变影响基本可以忽略。

(a) 孔径3 mm
1.3对试样拉伸试验过程的有限元数值模拟
1.3.1材料模型及模型参数标定
描述单调加载过程时,各向同性材料的力学行为可采用与Mises屈服函数相结合的等向强化模型:

(2)


(3)
有限元数值模拟采用ABAQUS。模型网格采用C3D8单元,为精准计算颈缩过程,颈缩段网格采用细化网格,见图3。与实验加载一致,试样一端固定,另一端进行位移加载。应用上述模型还需要真应力—对数塑性应变曲线。该曲线颈缩前的部分可由光滑圆棒试样单拉试验记录的位移—载荷曲线换算得到,如图4所示。拉伸过程中试样出现局部颈缩之后,试样标距段的应变分布不再均匀,对应这一过程的应力应变曲线需要参照实测位移—荷载曲线记录通过有限元模型计算来标定[17]。标定得到完整的真应力—对数塑性应变曲线,见图4。将该曲线用于数值模拟可得到位移—荷载曲线和颈缩局部轮廓线。与相应实测结果比较,数值模拟与实测结果吻合很好,如图5和图6所示,从而证实了图4标定后曲线的合理性。

图3 光滑圆棒试样模型网格划分

图4标定前后材料的应力—应变曲线
Fig.4True stress vs.plastic strain curve before and after calibration
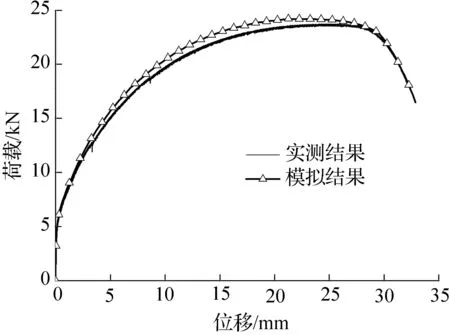
图5光棒试验和数值模拟的位移—载荷曲线
Fig.5Force vs.displacement curve of test and numerical simulation

图6 光棒试样试验和数值模拟得到的颈缩轮廓比较Fig.6 Comparing the outline of specimen necking area between test and computation
1.3.2孔板试样宏观变形的有限元模拟
孔板试样的有限元模型网格以d12t4模型为例,见图7,单元类型为C3D8R。d3t4模型单元数最少,为5 112个,d12t8模型单元数最多,为13 616个。为得到更精确的孔边应力应变分布,划分网格时在孔边处进行细化。为提高计算效率,利用试样几何和受力的对称性,只取试样的1/8建立模型。在试样3个对称面上,采用相应的法向位移约束来保证对称性。与实际情形一致,数值模拟用位移方式控制加载。各试样的试验和数值模拟得到的位移—载荷曲线见图8。由图8可知数值模拟与试测结果吻合较好。

图7 d=12 mm,t=4 mm试样的有限元模型

(a) 孔径3 mm
孔边是试样变形最大的区域,在纵向拉伸作用下圆孔变成了椭圆孔,试验中孔长轴与短轴之比的变化过程见图9。可通过比较各试样实测和数值模拟起裂时刻孔的长轴与短轴之比值的差异来检验数值模拟结果的合理性。由图10可见,各试样圆孔变形数值模拟与实测结果吻合较好,偏差最大的d6t4试样的误差也在5%以内。

图9试验过程孔长短轴之比(a/b)的变化
Fig.9The change of the ratio of longest/shortest axis length of the hole for different specimens

图10裂纹萌生时数值模拟与实测试样孔长短轴之比值的比较
Fig.10Comparison of longest/shortest axis length ratio for the holes of specimens between test and simulation at the crack initiation
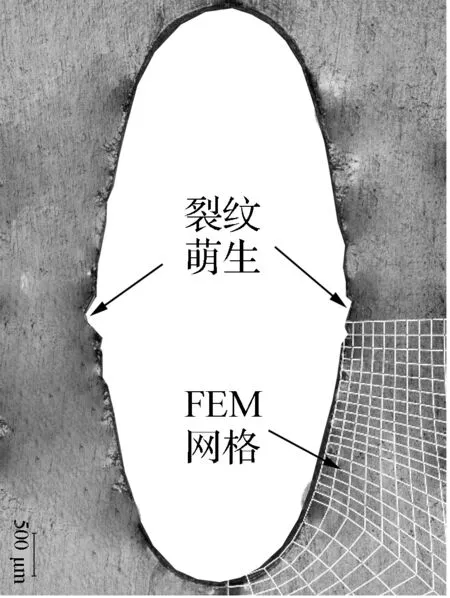
图11 孔板裂纹萌生时孔的变形——实测与数值模拟的比较Fig.11 Comparing the deformed hole of a center-hole specimen between test and simulation at the crack initiation
试样圆孔被拉长变形后,其实测与模拟结果对比情况见图11(限于篇幅,只给出一个典型结果)。
2 试样起裂位置
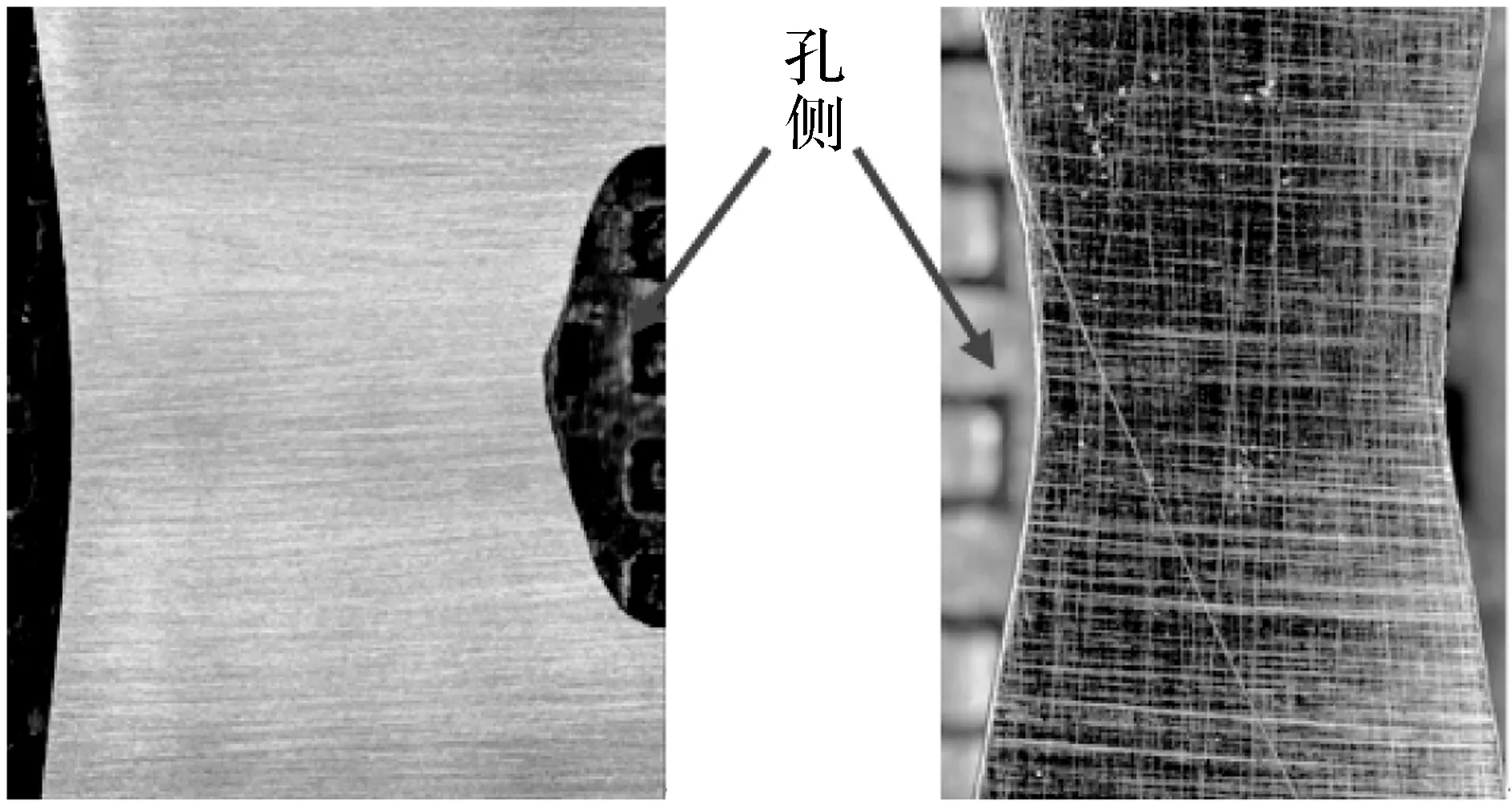
每种试样都进行了3次拉伸试验,且分别停止于不同时刻。当观察到试样裂纹萌生并且长度达到1 mm时停止第一次试验,此时裂纹都出现在试样最小横截面/纵平面交线与圆孔边相交处,见图11。为检查试样内部是否有裂纹,用线切割方法将试样在一半厚度处对称切开,抛光后在超景深三维显微系统下均没有观察到有裂纹,见图12(限于篇幅,仅给出孔直径为3 mm和12 mm、厚度为4 mm试样的剖面照片)。因此,可认为孔板试样均自孔边表面起裂。当表面出现较为明显裂纹后停止第二次试验。当试样拉伸至完全断裂时停止第三次试验。
(a) d3t4 (b) d12t4
(c) 试样剖切示意图
图12当裂纹在表面萌生时两个试样的厚度对称剖面
Fig.12The symmetric section of two specimens in thickness direction corresponding to crack initiation on specimen surface
观察上述试验,可将试样裂纹发展趋势展示于图13。可见,所有试样均沿最小截面断裂,裂纹萌生前该区域先经历了不同程度的颈缩。而裂纹扩展可分为两种类型。孔径为3 mm和6 mm的试样属第一种,如图13(a)所示[限于篇幅,将孔径3 mm、厚度4 mm的试样停止于3个时刻的局部照片展示于图13(a)]。可见,裂纹在纵向表面/最小截面交线与孔的交界处萌生后,厚度为4 mm和6 mm的试样,裂口先沿厚度方向发展直至贯穿,再沿最小截面韧带方向发展直至拉断;而厚度为8 mm的试样,裂口沿着厚度方向发展时,其孔厚度中心也会产生裂纹,再与孔边上下表面的裂口相贯通,之后沿最小截面韧带方向扩展直至拉断。孔径为12 mm的试样属第二种,如图13(b)所示。试样最小横截面/纵平面交线与圆孔边相交处裂纹萌生后,裂口中间区域很快也产生裂纹并迅速沿孔边厚度方向贯穿。此时裂纹沿韧带发展有所滞后,而试样在继续加载过程中继续颈缩,进而最小截面外边缘也出现裂口,由外而内最后整个截面迅速断开。
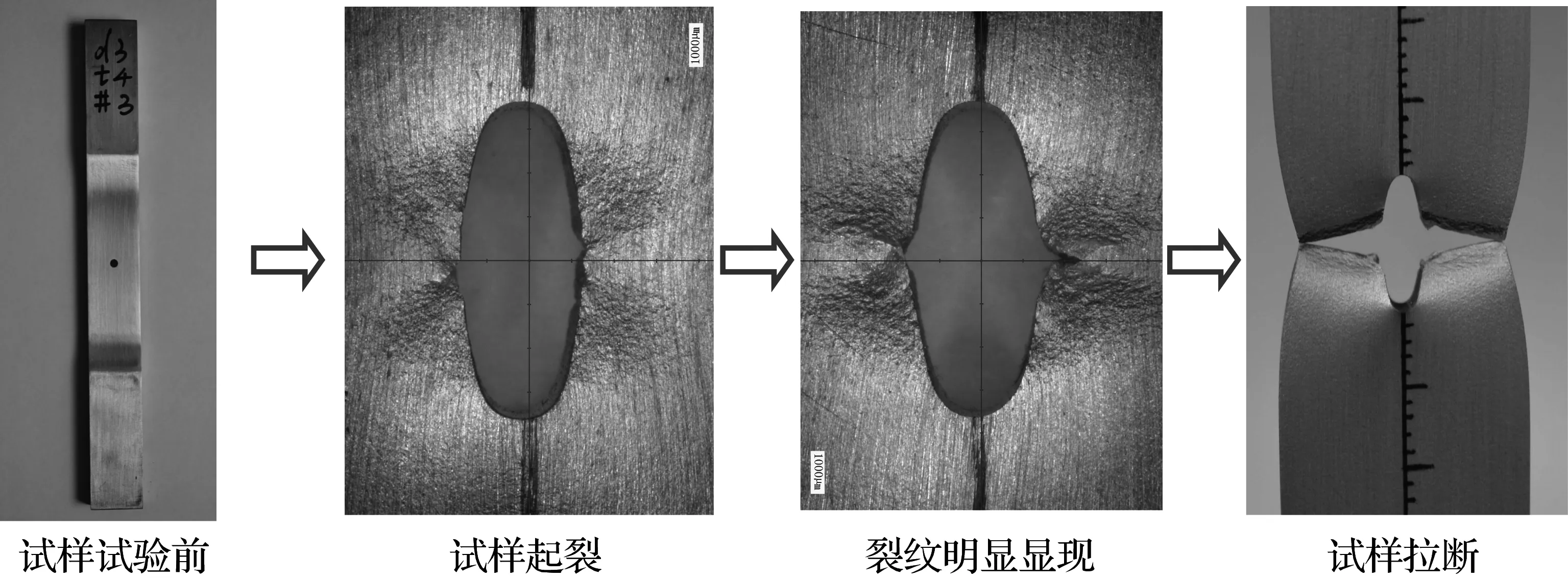
(a) 裂纹发展类型一

(b) 裂纹发展类型二
3 试样起裂处的断裂应变与应力三轴度
3.1断裂应变与应力三轴度的对应关系
材料的断裂应变是指材料试样起裂处在裂纹萌生时的应变,其数值与应力状态有关。断裂应变与应力三轴度的关系按以下步骤确定:①根据拉伸试验曲线和观测到的裂纹萌生时刻在试验曲线上确定破坏发生位置,该位置对应的试样标距段伸长记为ΔLf;②对各试样拉伸变形全过程进行有限元数值模拟,获得试样起裂时的应力应变分布;③参照实测试样起裂点,从数值模拟结果读出模型相应位置等效应变和应力三轴度数据,绘出等效应变—位移和应力三轴度—位移曲线;④按试样的ΔLf数值,确定该试样的断裂应变和对应的应力三轴度数值。于是,可描绘出用带中心圆孔平板拉伸试样的断裂应变—应力三轴度关系,如图14所示。
按有限元计算估计,图14中不同孔径中心孔板试样起裂时对应的应力三轴度在0.339~0.349,差别很小,小孔径试样孔边应力三轴度略大一些;而断裂应变值在0.72~1.1,孔径越小则断裂应变越大。该结果表明带中心圆孔平板拉伸试样的断裂应变对应力三轴度变化很敏感,随应力三轴度的增加而呈现明显的增加趋势(注意不是减小)。
将光滑圆棒试样和平板光滑试样测试计算数据[12]加入图14。可见,对应于图14中应力三轴度区间,断裂应变随应力三轴度增加是增加的,与Bao等[9]的结果定性相符。该结果与GTN模型、Rice-Tracey模型和McClintock模型所述的“应力三轴度提高导致材料的断裂应变下降”的结论是不同的。

图14 试样断裂应变与应力三轴度的关系
3.2韧带上的塑性应变与应力三轴度分布
考察韧带上的应变(包括等效应变和最大主应变)与应力三轴度的分布,可以探讨塑性应变和应力三轴度与材料断裂的相关性。由图15(a)和图15(b)中沿试样韧带—对称面交线的应力三轴度和应变分布曲线可知,裂纹萌生部位应力三轴度数值可近似看为1/3,而该处应变最大(孔边表面为自由表面,其与韧带交汇处近似于单轴拉伸状态,所以应力三轴度接近1/3)。孔造成的应变集中使得孔边应变远大于其他部位,因而裂纹萌生自孔边开始。此结果表明带孔平板试样可用于测试应力三轴度接近1/3时的材料断裂应变。
裂纹萌生始于韧带—孔边交线两个顶点(起裂点)。由图15(c)和和图15(d)中孔边厚度方向的应变和应力三轴度的分布可看出,大多数试样起裂发生时厚度中心处的应力三轴度和等效应变的数值均比起裂点的高,只有试样d12t4(厚度中心处应力三轴度比起裂点低)和试样d12t8(厚度中心处与起裂点相差不大)例外。因此可知,沿韧带/孔边交线,大部分试样裂纹萌生是在应力三轴度和应变都较小处。造成此现象的原因可能是:在拉伸过程中,圆孔表面特别是靠近韧带处因不均匀变形而变得非常粗糙(见图16),而起裂点处于两个自由表面交界处变形不均匀更为严重。而数值模拟没有考虑材料细观不均匀造成的变形不均匀,因此,裂纹萌生处实际应变要远较模拟计算的大。

(a) 韧带方向应力三轴度的分布
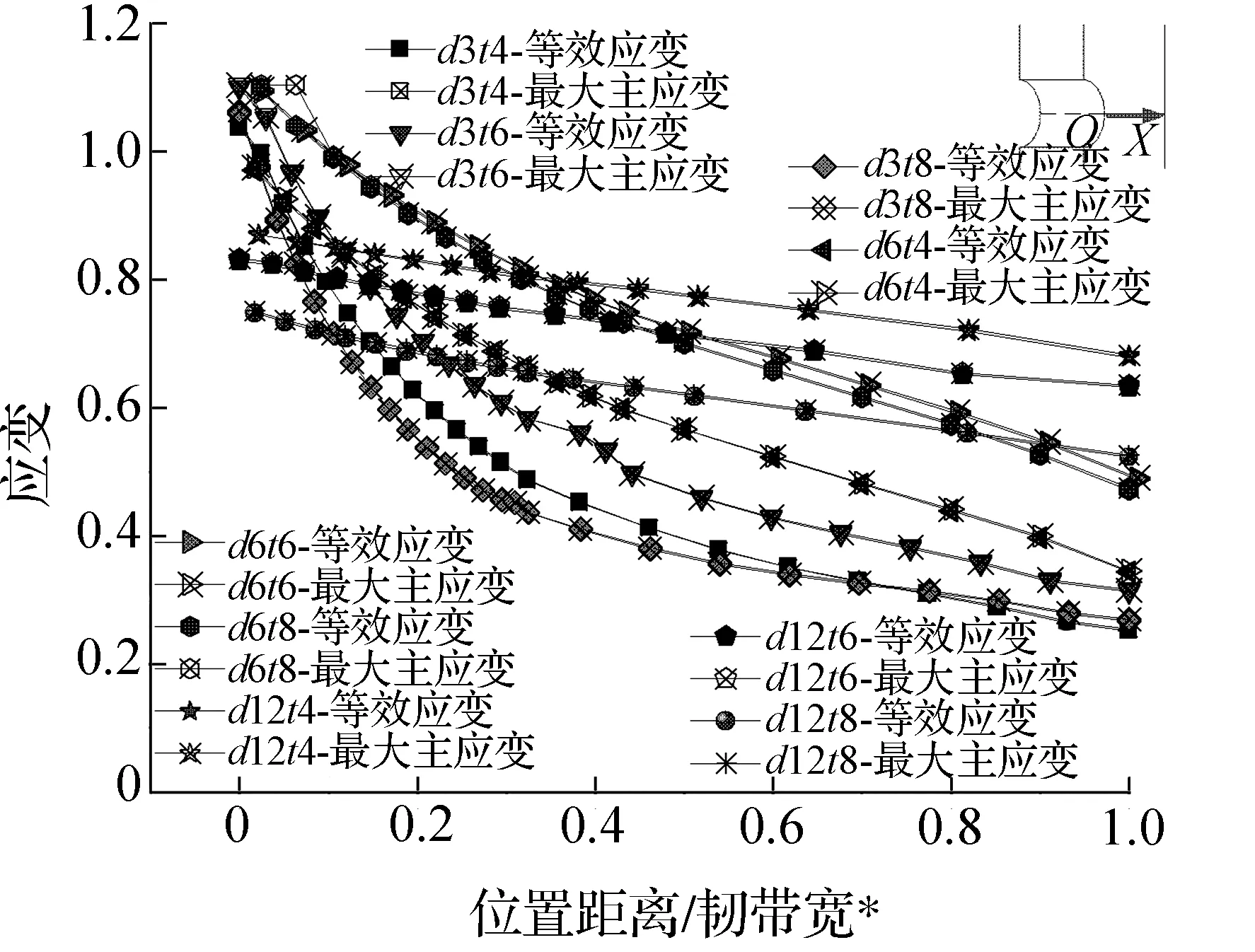
(b) 韧带方向应变的分布
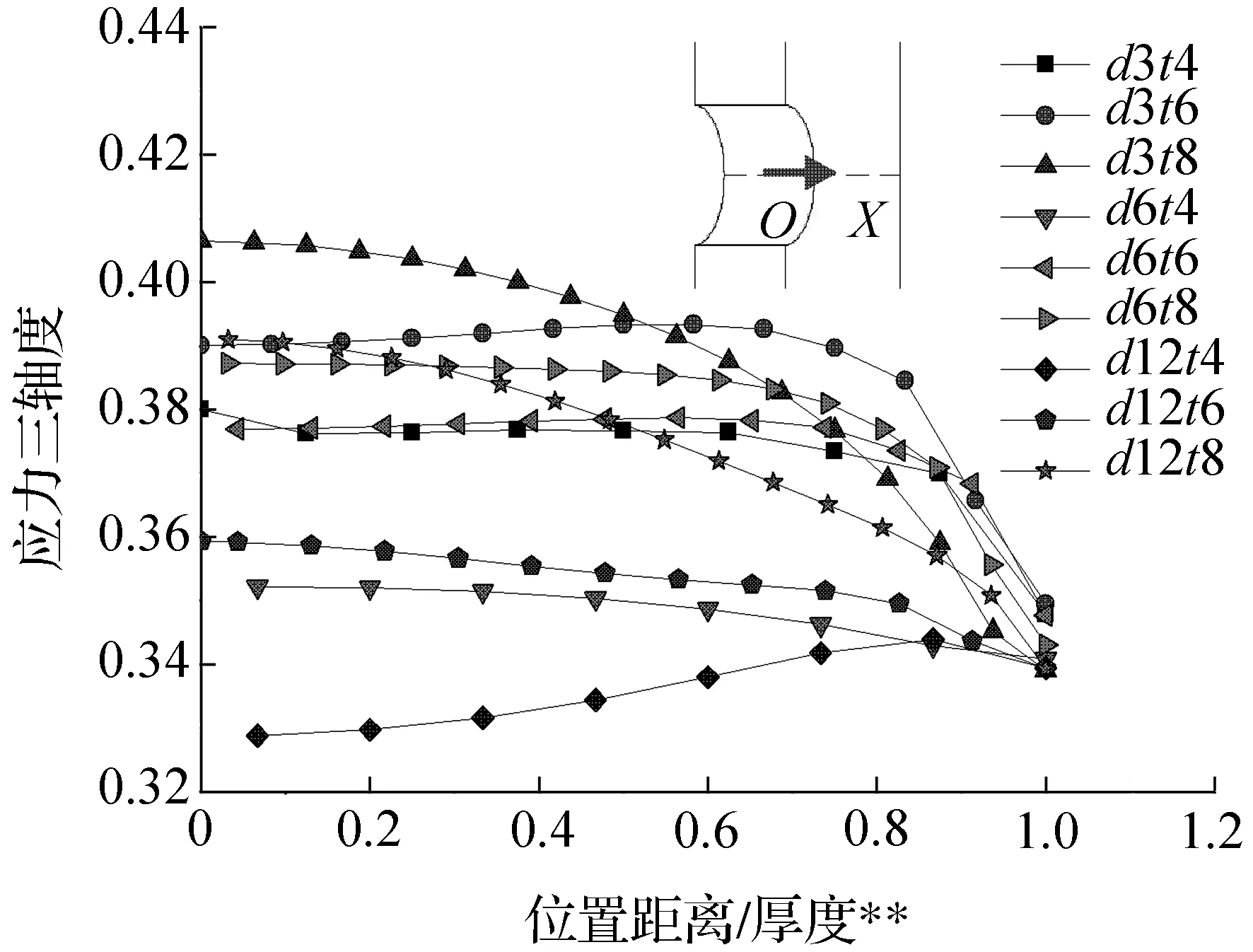
(c) 厚度方向应力三轴度的分布

(d) 厚度方向应变的分布
*.无量纲化横坐标(距离与试样韧带宽之比值),图中箭头OX所指方向为韧带方向;**.无量纲化横坐标(距离与试样厚度之比值),图中箭头OX所指方向为厚度方向
图15裂纹萌生时孔边韧带方向(厚度方向)的应力三轴度与应变分布
Fig.15Distribution of the stress triaxiality and strain along the ligament direction(thickness direction)at the crack initiation

图16 试样裂纹萌生处的粗糙表面
4 结 论
通过对9种不同厚度、不同孔径的纯铜中心孔板试样在MTS试验机上进行的系列单轴拉伸试验,结合数值计算和起裂点实测结果,对应力三轴度在1/3附近时的材料断裂应变进行了研究,根据带圆孔平板拉伸试样、光滑圆棒拉伸试样和文献[12]中的光滑平板拉伸试验的测试分析结果,得到以下结论:
①采用中心孔板试样可测得纯铜在应力三轴度数值为1/3时的断裂应变,而该应变远小于光滑平板和圆棒试样对应于应力三轴度在0.6~0.7的断裂应变。
②实测结果表明,材料断裂应变随应力三轴度减小而减小,与采用负指数函数描述断裂应变与应力三轴度关系的GTN和Rice-Tracey等模型明显不符。按这些模型估计的中心孔板试样的断裂应变应较光滑平板和圆棒试样拉伸试验测得数值明显偏大。
需要指出,带孔平板试样孔边表面粗糙,实际变形很不均匀,按连续介质力学方法估计的孔边断裂应变与实际值有误差,更准确的断裂应变估计需要进行细观力学分析。
[1]MCCLINTOCK F A.A criterion of ductile fracture by the growth of holes[J]. Journal of Applied Mechanics, 1968, 35: 363-71.
[2]RICE J R, TRACEY D M.On the ductile enlargement of voids in trixial stress fields[J]. Journal of the Mechanics and Physics of Solids, 1969,17: 201-17.
[3]GURSON A L.Continuum theory of ductile rupture by void nucleation and growth: Part I-Yield criteria and flow rules for porous media[J]. Journal of Engineering Materials & Technology, 1977, 99(1):2-15.
[4]TVERGAARD V, NEEDLEMAN A.Analysis of the cup-cone fracture in a round tensile bar[J]. Acta Metallurgica, 1984, 32(1): 157-169.
[5]周梦成, 冯飞, 胡建华,等.AZ31B镁合金断裂应变与应力三轴度的关系研究[J]. 中国机械工程, 2015,5:694-698.
[6]MALCHER L, ANDRADE PIRES F M, CÉSAR DE SJ M A.An extended GTN model for ductile fracture under high and low stress triaxiality[J]. International Journal of Plasticity, 2014, 54: 193-228.
[7]YU Q M.Influence of the stress state on void nucleation and subsequent growth around inclusion in ductile material[J]. International Journal of Fracture, 2015, 193(1): 43-57.
[8]黄西成, 陈裕泽, 朱建士.缺口试件拉伸试验中的材料失效函数确定方法[J]. 固体力学学报, 2008, 29(4): 385-388.
[9]BAO Y, WIERZBICKI T.A comparative study on various ductile crack formation criteria[J]. Journal of Engineering Materials & Technology, 2004, 126(3): 314-324.
[10]聂义珠.应力状态对材料破坏影响的试验和数值模拟研究[D]. 南宁:广西大学, 2008.
[11]张丽敏, 张克实, 石艳柯.纯铝试样厚度与缺口深度对拉伸破坏的影响[J]. 广西大学学报(自然科学版), 2009, 34(4): 438-443.
[12]李柳, 秦胜欢, 熊再银,等.T2纯铜平板剪切试样的大变形破坏试验研究[J], 广西大学学报(自然科学版),2015, 40(4): 890-896.
[13]汤安民, 王静.几种金属材料断裂形式变化规律的试验分析[J]. 实验力学, 2003, 18(4): 440-444.
[14]LI H, FU M W, LU J, et al.Ductile fracture: experiments and computations[J]. International Journal of Plasticity, 2011, 27(2): 147-180.
[15]贾东.镁合金MB2破坏模式与应力状态的关系[D]. 北京:中国工程物理研究院, 2013.
[16]BAO Y, WIERZBICKI T.On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanics Sciences,2004, 46(1): 81-98.
[17]ZHANG K S, LI Z H.Numerical analysis of the stress-strain curve and fracture initiation for ductile material[J]. Engng Fract Mech, 1994,49:235-241.
(责任编辑唐汉民裴润梅)
Study on tensile fracture of pure copper plate with a center hole
CAI De-liang, QIN Sheng-huan, GAO Liu, LIU Gui-long, ZHANG Ke-shi
(College of Civil Engineering and Architecture,Key Laboratory of Ministry Education of Engineering Disaster Prevention and Structural Safety, Guangxi University,Nanning 530004,China)
In order to study the fracture strain under a stress triaxiality close to 1/3, tensile experiments were conducted on a series of pure copper plate specimens with a center hole and different thickness. Numerical study and microscopic observations were carried out to determine the location where the fracture initiated, the value of stress triaxiality and the fracturet strain. On this basis, further investigations on the relationship between stress triaxiality and fracture strain of a material was carried out by comparing the experimental results with those from the smooth specimens under tension. The analysis results show that: ① Material fracture strain decreased with the decrease of stress triaxiality, which is seemly different from the ductile fracture law derived from void models; ②The actual deformation of the hole surface is very inhomogeneous, which is significantly higher than the value calculated by the continuum mechanics methods.
T2 copper;large strain tensile;numerical simulation;stress triaxiality;fracture strain
2016-03-17;
2016-04-20
国家自然科学基金资助项目(11472085,11272094);广西科技开发计划项目(1599005-2-5)
张克实(1954 —),男,广西桂林人,广西大学教授,博士,博士生导师;E-mail: zhangks@gxu.edu.cn。
10.13624/j.cnki.issn.1001-7445.2016.1178
O346.1+2
A
1001-7445(2016)04-1178-09
引文格式:蔡德良,秦胜欢,高柳,等.纯铜中心孔板拉伸断裂的实验研究[J].广西大学学报(自然科学版),2016,41(4):1178-1186.
