橡胶试验方法(五十九)
——摘自日本《ゴム試驗法》
2016-08-30王作龄张卓娅编译
王作龄 张卓娅 编译
橡胶试验方法(五十九)
——摘自日本《ゴム試驗法》
王作龄张卓娅编译
附录1 测定值的处理方法
附1.1 前言
在通常的试验或实验中,通过严格地遵从预先规定的程序可得到1个或多个测定结果。
这些测定值可以是连续的或离散的。且无论使用怎样精巧的仪器,怎样细心地观察,怎样正确地执行规定地程序,几次重复测定时得到的结果总是在某一特定值的左右产生离散变动。其主要原因有测定精度的局限和测定对象本质上的几率统计特点的影响。
就这样,测定值构成了实验的采样空间,按特定的分布函数分布。因此,如能采用某种方法找出该分布函数,则能够确定测定结果的最佳值,并能对测定结果的可信性进行评价。在此,从其侧面对试验和测定值的处理方法进行叙述。另外对客观判定测定值是否妥当的方法也一并加以介绍。
附1.2 求解测定值
附1.2.1 测定值的基本性质
(1)误差
测定值的变动是测定值与实际值的差引起的。误差的分类如附表1所示。

表1 误差分类
偶然误差是在完全不知其原因的情况下产生的。通过重复几次相同的测定可推断偶然误差的大小,求出接近实际值的测定结果。对实际值存在具有一定规律的测定误差时,该误差称为系统误差。系统误差分为三类,一是因测定设备不完善引起的机械误差,二是因测定者自身的一定习惯、性格引起的个人误差,三是因试验或实验条件规定或设定的不充分引起的理论误差。在弄清原因或倾向的情况下可以从测定值中除去误差值,但难以完全除去。一方面,正如从测定管理和共同实验所见,有时是把相同的试样分配给各实验室,再把得到的测定值收集到一处进行处理,例如在评价新提出的试验方法、试验装置的稳妥性而实施用于确认实验室内、实验室之间的重复性、再现性的ITP(Inter Laboratory Test Program)时就是如此。得到的测定值通常进行平均化操作。求取该测定值的平均值是从众多的测定值中求取最接近实际值的近似值的操作。平均操作意味着测定值的离散仅存在因偶然误差引起的情况。例如,因测定时的误差而出现与其他数据产生较大偏离的测定值时,不能把其拿来平均。因此,取平均值时,必须仔细琢磨是否存在偶然误差以外因素引起的离散数据。但是,是自己的设施时查明原因比较容易,而是别人的设施时就未必容易了。因此,在实施ITP时,首先必须要充分管理各实验室内的精度,提高并保持精密度。在精密度不够的情况下,作为评价实验室间再现性而提出的测定值未必能说是代表值。用于评价实验室间再现性而收集的测定值其室内重复性好当然是必要的,但属于实验室之间时,不容易排除仪器差、测定值、测定环境的影响。最终难以排除系统误差。产生极端偏离的测定值时,必须对提供该值的实验室进行查询,调查其有无技术性的异常原因。在不能确定原因时,妥当的做法是根据统计性校准来决定是否采用该偏离值。
(2)偏离值的确定
对极端偏离的测定值是否加以平均化操作必须用客观的方法判断。即进行统计性校准。作为偏离值的判断方法。在ISO 5725、JIS Z8402中记载了采取Grubhs校准、Cohcran校准、Mandelh、k统计量的校准方法[1]。在此于附 1.5.7节对Mandel方法进行介绍。
(3)测定精度
测定方法有直接测定和间接测定两种。前者是直接测定待测对象,把测定值作为直接结果,而后者是测定与待测对象有关的几个量,并通过计算测定值得出结果。测定精度因测定方法不同而异,但仅根据误差的大小进行讨论是不充分的。在直接测定中,相对误差定义为用实际值X与测定值x的差δX即绝对误差除以实际值得到的商ε[见式(1)]用来表示测定精度。但是由于 X值不能直接测定,而δX与x相比,绝对值较小。所以可以用式(2)表示。因此直接测定中的测定精度是由测定仪器能读取的最小单位δX与测定值的大小决定的。

间接测定中是欲求取的量Y与直接测定的量X1、X、X3…存在如式(3)的关系。

对式(3)进行全微分可得式(4).因此,
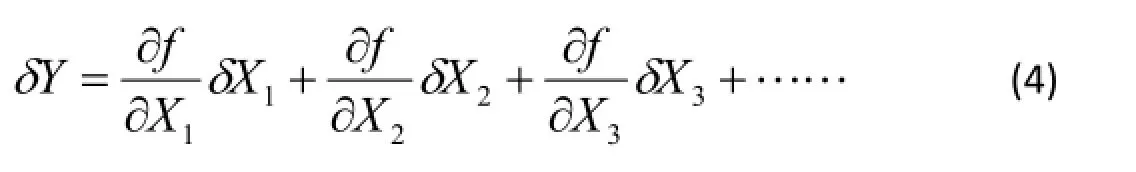
ε可表示为式(5),另外,如把y规定为Y
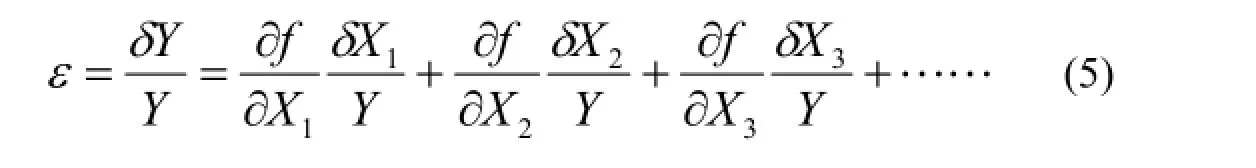
的间接测定值,则可得到测定精度的近似值,见式(6)。

例:研讨JISK6262中压缩永久变形率的测定精度。压缩永久变形率(%)可以由式(7)得到[2]。

式中,CS为压缩永久变形率(%);t0为试样初始厚度(mm);t1为试样从压缩装置取出 30min后的厚度(mm);t2为隔板厚度(mm)。现在,若设定以5%的精度测定CS(%)时,就必须研讨以何种精度分别测定 t0、t1、t2。如设:t0=12.70mm, t1=11.90mm、t2=9.52mm(则CS=25%)。
在这种情况下对式(7)两边取自然对数,以t0、t1、t2分别看作变量进行微分后可得式(8)。

因δ[CS]/[CS]的测定精度是5%,所以有

设 t0=12.70mm,t1=11.90mm,t2=9.52mm时,则:
δt0<0.06mm,δt1<0.04mm,δt2<0.16mm。因此,测定时一般采用可以读取至 0.01mm的标度测厚计就很好了。但试样在试验前后的厚度测定值必须有0.04~0.06mm的区别。
一般在试样标准和试验方法中对这些问题多已研究过了,测定方法也进行了合理的规定。但是在以解释新的现象为出发点而进行数据解析时,测定精度问题当然是重要事项。
附1.2.2 测定值的表示
(1)有效数字
读取至可测定的最小单位的测定值的数值称作有效数字,其位数称有效数字的位数。有效数字和有效数字位数在测定值的最终表示和测定值计算中的处理是非常重要的。
(2)测定结果的表示
测定结果的表示中必须考虑有效数字及其位数。例如:

在上例中,如果设2200的有效数字为前三位,则此三位数部分可从0.1~1000之间选择,然后添加上10的整幂数表示。如根据JISZ8203-2000[国际单位制(SI)及其使用方法][3],在此时的单位中采用组合单位Hz,则规定可以用10的整数幂或接头词来表示(表2)。

表2 接头词
(3)测定值之间的数值计算
有效数字问题在测定值之间进行数值计算时是重要的问题。
不用必要位数以上的测定值不是因为不需要高精度,而是测定精度不明确。相反,随意删除有效数字的位数可降低实验精度。一般来说,有效数字的位数随着数值计算的进行而减少。在四则运算中,有效数字的取舍方法如
①加减运算中,对测定值有效数字最后1位以后的数值进行计算没有意义。
②乘除运算中,需进行计算的两个测定值的有效数字位数不同时,计算结果的位数由最初的两个测定值中有效数字位数少的决定。
这样一来,最终结果的有效数字位数应该考虑各测定值的有效数字位数来确定[4]。
附1.3 测定结果的评价
测定值根据测定对象的性质依各种分布函数产生统计变化。但一般情况下,分布函数多为正态分布。因此,一般测定值的最可几值的求法及其可信度的评价方法以正态分布为前提。其详细内容在JIS Z9041-1999(数据统计解释方法)[5]中有规定。所以在此只作简要的摘录。
附1.3.1 频率分布
设某测定对象的实际值为 X,在排除系统误差后通过n次重复直接测定得到x1、x2、x3、…xn。作为数据的要约,首先必须抓住其整体性质。这时,制成频率分布图(也称直方图,柱形图,是对应于测定值x的频率/的分布)是有用的。根据该结果,可以知道①测定分布中心的倾向;②分布宽窄的程度;③分布变形的程度;④分布峰的程度等统计量的要点。据此应读能够捕捉到测定的代表值和大致的可靠性。
附1. 3.2 统计量的计算
(1)对测定值分布中心的倾向的测量
根据代表值的分布行为,式(9)可用于算术平均值、中位数、最可几值(方式)的计算。
算术平均值

(2)对测定值分布波动的测量——代表值的可信度
偏差平方和

分散

标准偏差

式(10)~式(12)的计算结果取0或正值,数值越大表示测定值的波动越大。
(3)表示测定值分布性质的测量——代表值的可信度
原点周围的一次因素

平均值周围的一次因素

这些数值被用于表示测定值分布的左右对称、变形和峰等的性质。
附1.3.3 分布函数
上述统计量的测量在测定值的要约方面的作用依测定值的性质或其统计行为稍微有些不同。例如:表示类似断裂物理量的极限性质的物理量测定值普遍遵从非正态分布的特殊分布函数,作为其测定代表值,最可几值比算术平均值更恰当。但在JIS K6251中设定的拉伸强度、伸长值的测定值采用比平均值更恰当的中心值,虽然测定值的最可几值是正确的。
下面给出代表性分布与代表值的关系。
(1)离散分布
a.二项分布 某事件A发生的几率在尝试1次时取P,在该尝试独立进行n次重复时,设事件A出现的次数为X(x=0,1,2…n),X=x的几率见式(15),平均值、标准偏差分别见式(16)、式(17)。

b.泊松分布 几率变量X取0、1、2、…,n,X=x时的几率用式(18)表示时,平均值、标准偏差分别用式(19)、式(20)表示。
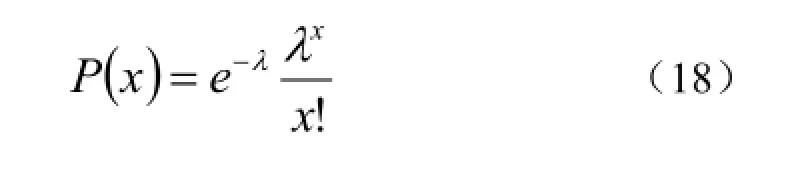
(2)连续分布
a.正态分布(Gauss)几率函数X的密度函数f(x)如式(21)时,平均值、标准偏差分别为式(22)、式(23)。
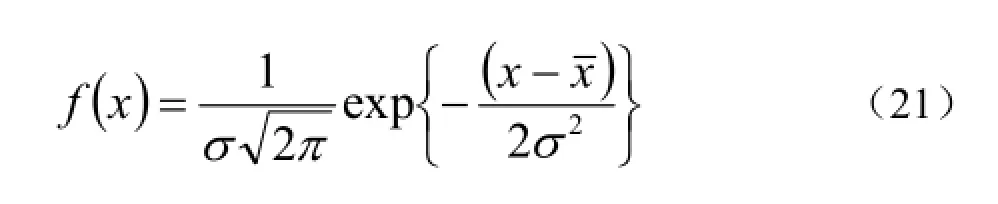
b.指数分布 几率密度函数、平均值、标准偏差分别为式(24)~式(26)。

c.γ分布 几率密度函数、平均值、标准偏差分别为式(27)~式(29)。

(未完待续)
10.3969/j.cn.12-1350(tq).2014.05.006
