基于PSO的抗扰动最少拍控制器设计
2016-08-29范孟豹吴根龙王禹桥杨雪锋
范孟豹, 吴根龙, 王禹桥, 杨雪锋, 李 威
(中国矿业大学 机电工程学院, 江苏 徐州 221116)
基于PSO的抗扰动最少拍控制器设计
范孟豹, 吴根龙, 王禹桥, 杨雪锋, 李威
(中国矿业大学 机电工程学院, 江苏 徐州221116)
在输入和扰动共同作用下,提出了基于粒子群优化(PSO)算法的最少拍控制器的自动设计方法。基于扰动作用下最少拍控制器的设计理论构建修正等式,然后根据等式两边对应项系数相等以建立适应度函数,进而应用粒子群优化算法求解修正等式中的未知数,以实现最少拍控制器的自动化设计。实例仿真发现,应用该算法和手工计算的结果一致,验证了该方法的可行性和准确性。研究结果为最少拍控制器的教学和工程应用提供了一种计算机辅助设计工具。
计算机控制; 最少拍控制器; 扰动抑制; 粒子群优化算法; 仿真
计算机控制技术是高端装备制造业的核心技术之一,计算机控制技术课程可使学生掌握综合运用所学的单片机、控制工程基础、测试技术、液压和电机等基础知识,解决工业生产中的控制问题的能力,从而提高企业自动化水平和生产效率[1-3]。
最少拍控制器是计算机控制技术课程的教学重点和难点内容之一,是控制器数字化设计方法的典型代表[4-5]。最少拍控制是指在最短的时间内使系统达到稳态,能全面改善控制系统的快速性、准确性和稳定性,在工业中有着广泛的应用。Tsuyoshi K等[6]采用最少拍控制实现了单相多功能交互式逆变器与基于FPGA的硬件控制器;叶凌云等[7]运用最少拍无波纹算法实现了高精度动态标准源反馈控制;文献[8]介绍
了最少拍控制器在滞后一拍输出方式下逆变器控制中的应用;文献[9]介绍了三相脉宽调制整流器的最少拍控制器设计。与常规的PID控制器相比,最少拍控制器的独特之处在于需要根据系统的输入信号类型、被控对象传递函数及采样周期而设计。因此,当上述条件中的任意一个发生变化时,最少拍控制器均需要重新设计,以使系统性能达到最优。现有教材和文献几乎均是以手工计算的方式完成最少拍控制器设计,存在计算量大、重复设计等缺点。
在文献[10]提出了最少拍无波纹控制器的自动设计算法,但是该算法的设计并没有考虑扰动抑制。很多情况下影响控制系统输出的不仅有输入信号,还有扰动信号,因此控制器的设计需要考虑对输入的跟踪性能和对扰动的抑制能力,最少拍控制器的设计亦是如此。针对最少拍控制器手工设计方法的不足,在只考虑输入作用的前提下,作者提出了基于粒子群算法的最少拍控制器的设计方法。当考虑输入和扰动两类信号时,最少拍控制器设计分两步[1]:第一步在不考虑扰动的情况下设计控制器;第二步验证设计的控制器是否可以使扰动引起的稳态误差为零,如果为零,则设计结束,如果不为零,则需要修改设计的控制器。修改最少拍控制器需要确定若干未知参数,且当设计条件发生变化时控制器的修改设计也需要重新进行。鉴于此,在前期的工作基础上,本文将粒子群算法用于输入和扰动共同作用下最少拍控制器的设计,以实现控制器设计的自动化。
1 考虑扰动的最少拍控制器设计理论
通常,存在干扰作用的计算机控制系统原理框图见图1。
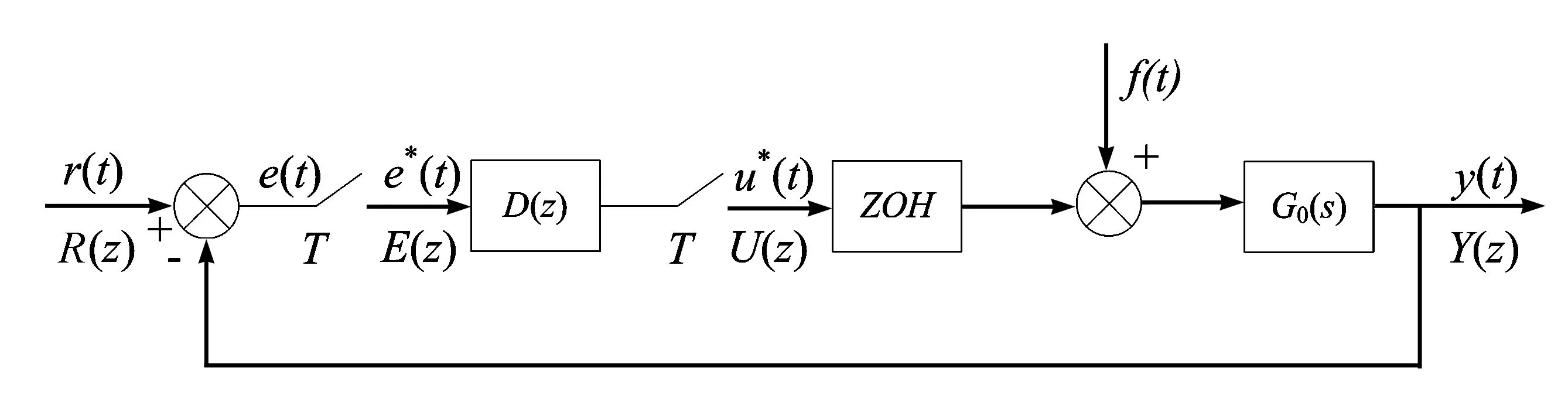
图1 存在干扰作用的计算机控制系统的原理框图
参考输入R(z)和扰动作用F(z)共同作用下,最少拍控制器D(z)设计如下[1]:
(1) 不考虑扰动作用,仅考虑输入作用下控制器D(z)设计,则有
(1)
式中W(z)为系统闭环Z传递函数,We(z)为误差闭环Z传递函数,G(z)为被控对象的Z传递函数。
(2) 扰动信号与被控对象在复数域的乘积离散化化为G0F(z),仅考虑扰动作用时系统Z传递函数:
(2)
验证Wf(z)是否满足扰动抑制要求,即稳态误差为0。若使扰动作用下的稳态误差为0,需满足:
(3)
式中:m由扰动信号Ff(z)的型次决定,m=1,单位阶跃信号,m=2,单位速度信号,m=3,单位加速度信号;Ff(z) 为不含(1-z-1)因子的关于z-1的有限多项式。
如果Wf(z)满足式(3),则扰动控制下的与不考虑扰动作用下最少拍控制器相同,不需要修改。
若Wf(z)不满足式(3),则需要修正控制器,修正等式为
(4)
式中A(z)为所设关于z-1的多项式,其包含Wf(z)中所有极点,不失一般性,A(z)和Ff(z)可设为如下形式:
(5)
式中pi为Wf(z)中的第i个极点,Q1(z)=1+k1z-1+…+km+v-uz-(m+v-u),u为Wf(z)的零点个数,v为不稳定极点个数。
具有扰动抑制能力的数字控制器表达式为
(6)
2 粒子群优化算法
根据前文的控制器设计理论,最少拍控制器自动设计的难点在于求解修正等式(4)中的未知系数。粒子群优化算法PSO(particle swarm optimization)最早由Eberhart教授和Kennedy博士[11]受鸟群觅食行为启发于1995年提出的一种迭代优化算法,具有简单、收敛速度快、精度高且适应性强等优点,已广泛用于求解工程优化问题[12-13]。
针对标准粒子群算法存在的不足,Cheng等提出了社会学习粒子群优化算法(SLPSO)[14]。社会粒子群优化算法在求解问题时,会将每个粒子按照自己的适应度值大小进行排序,根据每个粒子的学习可能性定义其更新速度,这是社会学习粒子群算法区别于常规粒子群算法的关键,粒子的更新速度更合理,从而大大提高了最优解搜索速率。

p(j,:)为粒子位置,每个粒子的初始速度均为0。首先将空间中每个粒子经评价函数对应的适应度值存入适应度值矩阵中,该矩阵为r行1列,其中适应度值顺序与群空间中粒子的顺序一一对应。然后对适应度值矩阵中数据由大到小进行排序,并按照新的顺序将粒子位置和速度也重新排序。通常,适应度值越小解越接近最优解。因此每次迭代之后全局最佳适应度值bestf=fitness(r),与此同时,对应的最优解为bestp=p(r,:)。
粒子排序之后,其他粒子向拥有最佳适应度值的粒子学习。拥有最佳适应度值的粒子将不进行学习,定义第i个粒子的学习可能性为[14]
(7)
式中系数α通常小于1,现取α=0.5。根据粒子学习可能性定义每个粒子的速度更新公式为
(8)
式中,v1为每个粒子的速度更新公式,其与自身学习可能性相关,表达式如下:
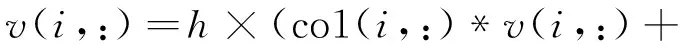
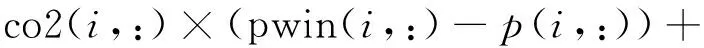
(9)
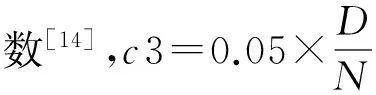
(10)
为了保证更新后的粒子位置和速度限定在最优解可能存在的空间内,必须要设定粒子位置和速度的变化范围。当随机产生的位置或者速度超出变化范围时,要及时进行约束,以避免结果发散。粒子位置的约束条件为
(11)
粒子速度的约束条件为
(12)
粒子群算法通过反复迭代计算以获取待求问题的最优解。每次迭代之后全局最佳适应度值和全局最优解都需要更新,其更新方式如下:
全局最佳适应度值更新公式为

(13)
全局最优解更新公式为:

(14)
3 最少拍控制器
3.1适应度函数建立
由式(4)和式(5)可以看出,考虑扰动的最少拍控制器的设计关键在于确定A(z)的未知参数k1, … ,km+v-u与Ff(z)未知参数a0,a2, … ,av,即多维函数优化问题。鉴于此,可以将粒子按顺序编码为(k1,…,km+v-u,a1,a2, … ,av)。A(z)和Ff(z)满足Wf(z)修正等式:Wf(z)A(z)=(1-z-1)mFf(z)。
根据上式,适应度函数定义为修正等式左右两边对应项系数差的绝对值。显然,当适应度值越小,说明控制参数越接近期望稳定值。当适应度值等于0时,等式(4)两边对应项系数相等。此时,粒子群算法的最优解即为式(4)中的待求参数值。
3.2算法流程
考虑扰动作用下,应用粒子群优化算法设计最少拍控制器的算法流程如下:
Step1:将系统开环传递函数G0(s)离散化为Z传递函数G(z),根据分析输入信号类型选择对应的闭环Z传递函数W(z)和闭环误差Z传递函数We(z)。
Step2:由扰动信号类型得到G0F(z),进而通过式(2)可求得Wf(z),计算Wf(z)的零点、极点和增益。
Step3:根据Step2中提取的零点中是否含有m个1来判断Wf(z)是否满足式(3),如果满足,则控制器D(z)由式(1)来计算;否则,继续向下运算。
Step4:初始化粒子群种群规模、迭代次数、初始位置的边界、最佳适应度值、最优解位置等参数,并随机产生粒子位置和速度。
Step5:计算并将每个粒子的适应度值存放在适应度值矩阵fitness中,然后对fitness中数据按从大到小排序,同时把粒子位置和速度也按照更新后的fitness顺序重新排列,再根据式(13)和式(14)更新群体最佳适应度值和群体最优解。
Step6:根据式(8)和式(10)更新粒子速度和位置,计算每个粒子的学习可能性PL。
Step7:若满足循环跳出条件,则结束运行,输出最终结果,否则返回Step5。
4 数值仿真及结果分析
设定被控对象的传递函数为:
采样时间0.025 s,设计最少拍有波纹控制器,扰动为单位阶跃信号。设定粒子群算法的粒子基群规模N=50,迭代次数M=30,加速因子h=0.8。
4.1输入为单位阶跃信号
在输入为单位阶跃信号时,经验证控制器不满足扰动抑制扰动的要求,需要修改。根据式(4)和(5)可知,需要求解3个未知参数k、a、b,其参数的取值范围分别为[0, 3],[-2, 0]和[-1, 2],最大迭代次数为30。应用手工和本文所提算法得到的参数k、a和b的值见表1。修正后的最少拍无波纹控制器为
(15)
算法运行过程中,适应度函数值及待求参数k、a和b值的变化分别如图2和图3所示。从表1可知,应用本文算法求得的参数k、a和b值与手工计算结果完全一致,证实了本文算法的可行性与准确性。

表1 单位阶跃信号时手工与本文算法计算的控制参数对比
由图2可以看出,算法大约经过20次迭代之后,适应度值趋近于0,适应度值满足要求,未知参数也趋于稳定,稳定值即为待求的参数值。

图2 输入为单位阶跃信号时适应度值变化曲线

图3 输入为单位阶跃信号时待求参数变化曲线
为了进一步验证算法的正确性,利用simulink仿真工具建立的仿真原理结构见图4。单位阶跃输入和单位扰动共同作用下的系统输出见图5。分析发现,系统在短暂振荡之后达到稳态,且稳态误差为0,符合系统设计要求。
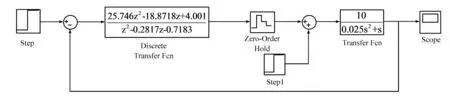
图4 考虑扰动的最少拍控制系统仿真原理结构

图5 输入为单位阶跃信号的系统输出响应
4.2输入为单位速度信号
输入为单位速度信号时,经验证控制器不满足扰动抑制扰动的要求,需要修改。根据式(4)和(5)可知,需要求解3个未知参数k、a、b,其参数的取值范围分别为[0, 2],[-1, 1]和[0, 2],最大迭代次数为30。应用手工和本文所提算法得到的参数k、a和b的值见表2。修正后的最少拍无波纹控制器为
(16)
算法运行过程中,适应度值及待求参数k、a和b值的变化分别如图6和图7所示。从表2可知,应用本文算法求得的参数k、a和b值与手工计算结果完全一致,证实了本文所提算法的可行性与准确性。

表2 单位速度信号时手工与本文算法计算的控制参数对比
由图6可以看出,算法大约经过20次迭代之后,适应度函数值趋近于0,适应度值满足要求,控制参数也达到稳定状态,稳定值即为所求控制参数值。
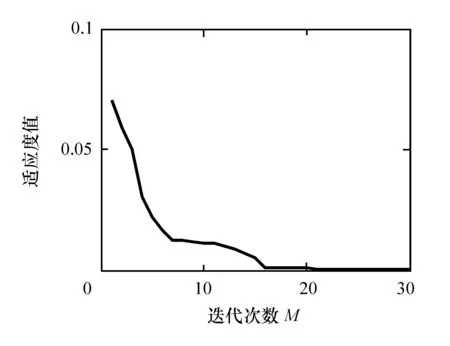
图6 输入为单位速度信号时适应度值变化曲线
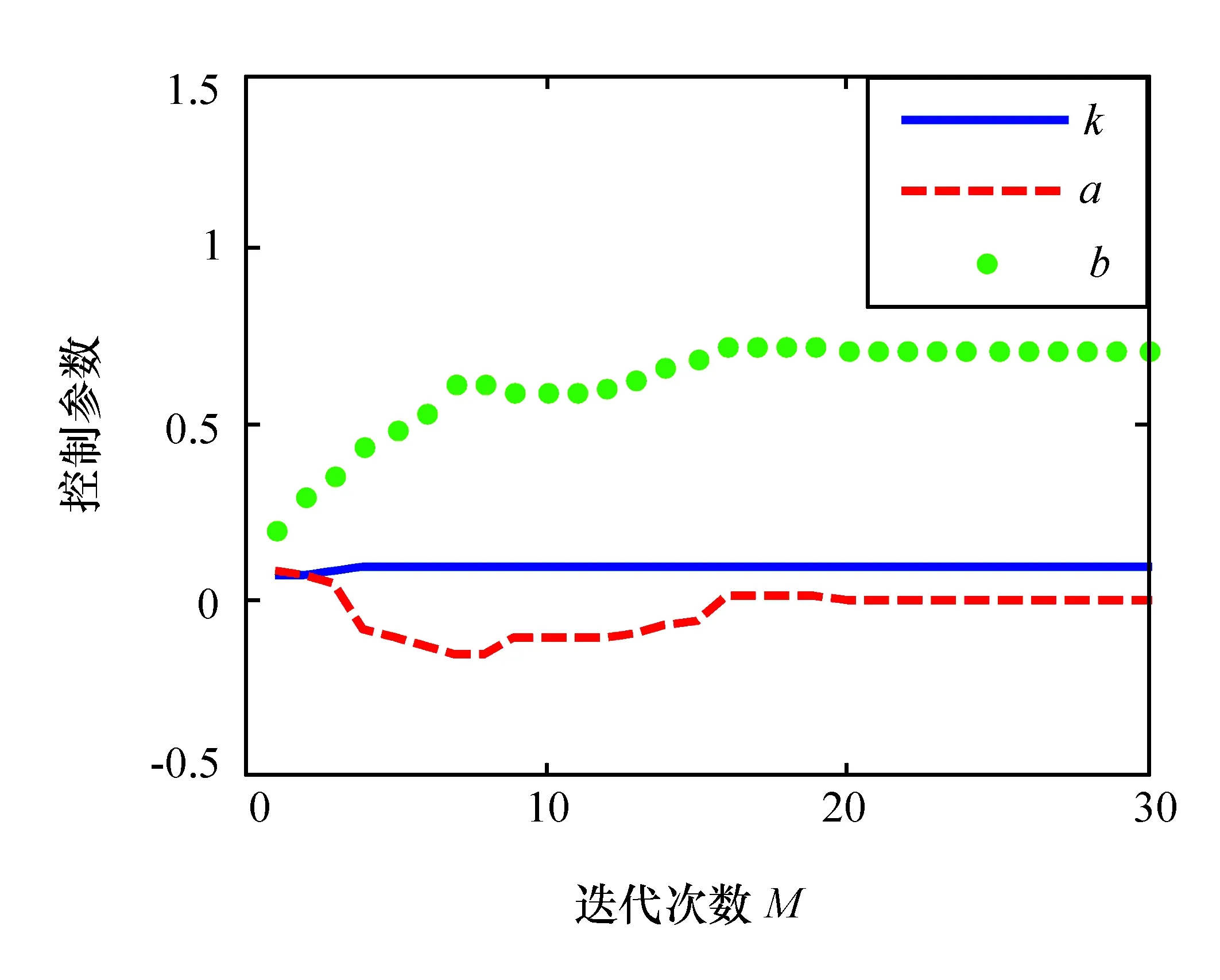
图7 输入为单位速度信号时待求参数变化曲线
为了进一步验证算法的正确性,利用simulink仿真工具构造的仿真原理结构见图8。单位阶跃输入和单位扰动共同作用下的系统输出如图9所示。分析发现,系统在短暂振荡之后达到稳态,且稳态误差为0,符合系统设计要求。
5 结论
根据扰动作用下最少拍控制器的设计理论,在控制器需要修正的情况下构造了修正等式,且构造的修正等式两边对应项系数应相等。据此建立了适应度函
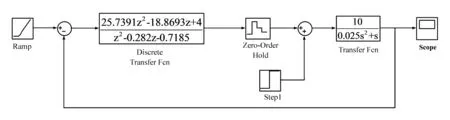
图8 输入为单位速度信号、考虑扰动的最少拍控制系统仿真原理结构图
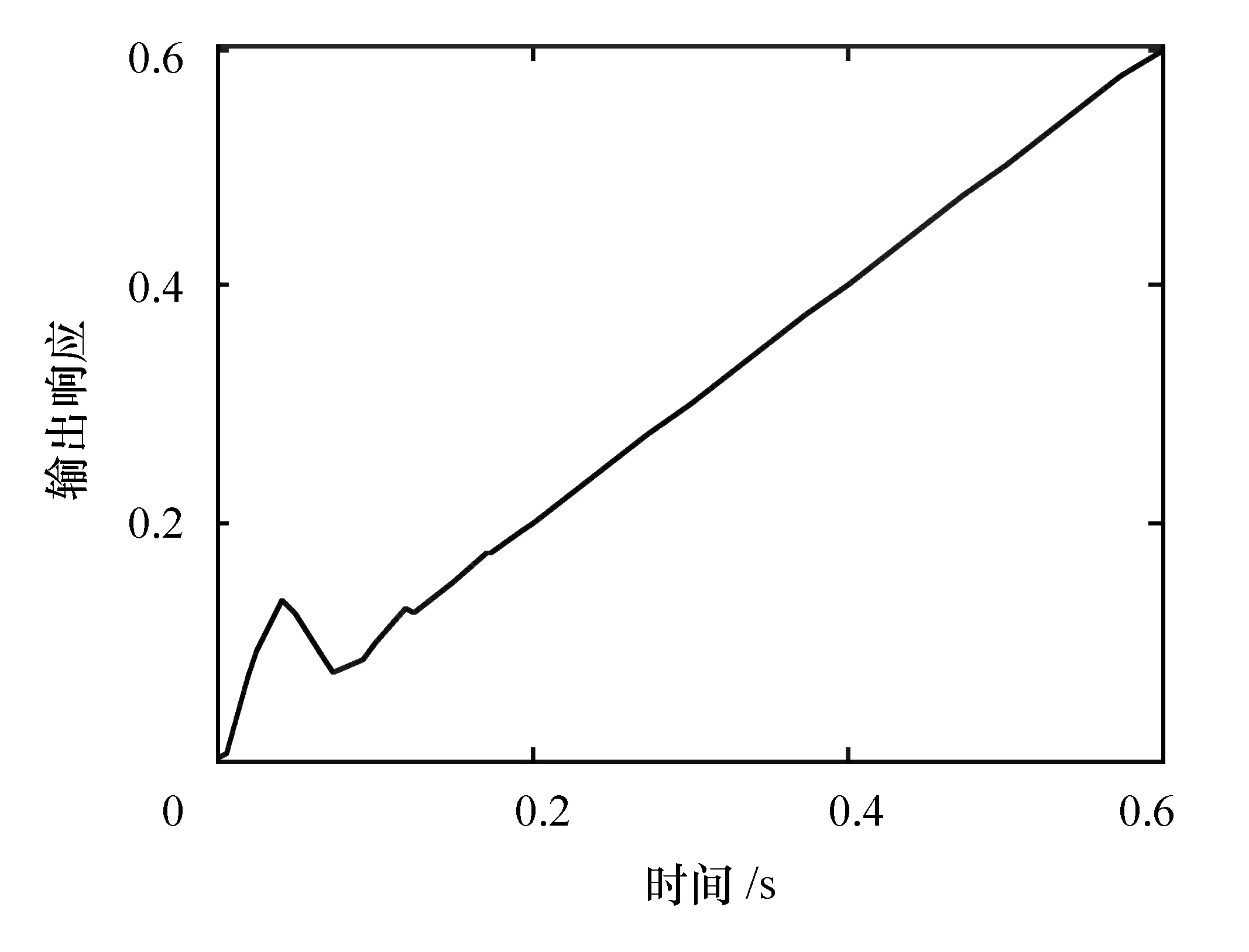
图9 输入为单位速度信号的系统输出响应
数,并应用社会学习粒子群优化算法求得修正等式中的未知系数,从而实现最少拍控制器设计的自动化。实例仿真结果表明,手动方法与本文所提算法得到的结果是一致的,验证了本文算法的可行性与准确性。本文研究结果为计算机控制技术课程教学中考虑扰动的最少拍控制器的理论与实验教学、工程应用提供了一种计算机辅助设计工具,解决了最少拍控制器设计过程中由于对象参数、采样周期变化需要重复计算导致的计算量大的问题。
References)
[1] 姜学军, 刘新国, 李晓静.计算机控制技术[M].2版.北京: 清华大学出版社, 2010.
[2] 王富昕, 曲学楼, 李双丰. 创新型计算机控制实验教学系统的研制及实现[J]. 实验室研究与探索, 2011,30(3):77-79,99.
[3] 高兴泉, 王立国. 基于SIMULINK/SIMSCAPE的计算机控制系统仿真实验平台[J]. 实验技术与管理, 2013,30(9):88-92.
[4] 马常旺, 林卫星, 谢建军, 等. 计算机控制技术实验课的改革与实践[J]. 实验技术与管理, 2004, 21(2):125-128,138.
[5] 张智焕, 张惠娣. 机械工程控制的虚拟仿真实验教学实践[J]. 实验技术与管理, 2014,31(7):102-103,111.
[6] Tsuyoshi K, Kenji A, Eigo S, et al. Current Control Method Using Voltage Deadbeat Control for Single Phase Utility Interactive Inverter with FPGA based Hardware Controller[C]//IECON 2004. 30th Annual Conference of IEEE, 2004:1594-1599.
[7] 叶凌云, 陈波, 张建, 等. 基于最少拍无波纹算法的高精度动态标准源反馈控制[J]. 浙江大学学报:工学版,2013,47(9):1554-1558.
[8] 姚玮, 吕征宇. 滞后一拍输出方式下逆变器的最少拍控制[J]. 电力自动化设备, 2014,34(7):9-14.
[9] Zhang Yongchang, Xie Wei, Zhang Yingchao. Deadbeat Direct Power Control of Three-phase Pulse-width Modulation Rectifiers[J]. IET Power Electronics, 2013, 7(6):1340-1346.
[10] 范孟豹, 董事, 王禹桥, 等. 基于粒子群算法的最小拍无波纹控制器设计[J]. 实验技术与管理, 2015, 32(9):80-83,87.
[11] Kennedy J, Eberhart R. Particle Swarm Optimization[C]//Proceedings of IEEE International Conference on Neural Network. Piscataway, N J,1995:1942-1948.
[12] 李爽, 王志新, 王国强. 基于改进粒子群算法的PIDNN控制器在VSC-HVDC中的应用[J]. 中国电机工程学报, 2013,33(3):14-21.
[13] 史永丽, 侯朝桢, 苏海滨. 基于粒子群优化算法的自抗扰控制器设计[J]. 系统仿真学报, 2008, 20(2):433-436.
[14] Cheng Ran, Jin Yaochu. A Social Learning Particle Swarm Optimization Algorithm for Scalable Optimization[J]. Information Sciences, 2015(291):43-60.
Design of disturbance rejection deadbeat controller based on PSO
Fan Mengbao,Wu Genlong, Wang Yuqiao, Yang Xuefeng, Li Wei
(School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China)
The aim is to propose an method for automatic design of disturbance rejection deadbeat controller based on PSO(particle swarm optimization). Firstly, an equation, which contains unknown variables to be determined, was developed to modify deadbeat controller for improvement of disturbance rejection according to the design theory of deadbeat controller. Secondly, the fitness function was created, as coefficient of the left-hand side term with the same power should be equal to that of the right-hand side term for the developed equation. Thirdly, the unknown variables were determined automatically using particle swarm optimization without any manual intervention. Finally, simulations demonstrate that the results from the presented method are equal to those from manual design, which verifies the feasibility and effectively of the presented method. This work offers a valuable CAD tool, and it facilitates the teaching, experiment and practical application of deadbeat controller.
computer controlled system; deadbeat controller; disturbance rejection; PSO(particle swarm optimization); simulation
DOI:10.16791/j.cnki.sjg.2016.04.011
2015- 10- 21修改日期:2016- 01- 16
国家863计划资助项目(2012AA041806);国家自然科学基金资助项目(51307172);江苏省六大人次高峰资助项目(ZBZZ-041);江苏省自然科学基金资助项目(BK2012567);高等学校博士学科点专项科学基金项目(20120095120027)
范孟豹(1981—),男,山东高唐,博士,副教授,系主任,研究方向为控制理论及应用、电磁无损检测技术.
E-mail:wuzhi3495@cumt.edu.cn
TP273
A
1002-4956(2016)4- 0038- 05
