陶瓷谐振器特性分析与参数测量

刘小艳, 陆延丰

(清华大学 电子工程系实验教学中心, 北京　100084)



陶瓷谐振器特性分析与参数测量

刘小艳, 陆延丰

(清华大学 电子工程系实验教学中心, 北京100084)

采用等效电路模型和组合测量法研究陶瓷谐振器的特性,测试其等效电路参数。实验结果表明,该方法完全可行,且简单实用,电路实验室一般均具备实验条件。该方法可供使用者了解陶瓷谐振器的特性或用于电路的CAD仿真,也可用于压电材料和元器件的特性参数测试,该实验研究的内容也非常适用于电子电路实验教学。

陶瓷谐振器； 等效电路参数； 组合测量法； Matlab计算

当外加一交流电场时,陶瓷谐振器和石英晶体就会产生机械振动；反之,若外加一机械压力,陶瓷谐振器和石英晶体会产生电场,这种物理现象称为压电效应。当外加交流电场的频率与它们的谐振频率相当时,机械振动的振幅比其他频率时大得多,这种现象称为压电谐振[1]。陶瓷谐振器和石英晶体均具有高稳定、无需调节、抗干扰性强等特点,广泛应用于各种电子产品如玩具、家电、数码产品中,用来产生频率稳定度很高的基准时钟信号、选频和稳频等[2]。石英晶体的频率精度要高于陶瓷谐振器,但成本也比陶瓷谐振器高。

随着近年来压电陶瓷技术的发展和压电陶瓷新材料的涌现,能达到的工作频率越来越高,随之而来的应用也越来越广泛[3-7]。压电元器件特性的测量技术也得到更多关注,已成为高校教学实验研究的重要内容[8-11]。本文采用一种简单实用的实验方法研究陶瓷谐振器的特性,利用组合测量法实现其等效电路模型参数的测试。一方面这些模型参数可用来进行陶瓷谐振器的CAD仿真以指导具体电路的应用,另一方面该实验所用的测试方法和电路也非常适用于高校电子电路实验教学。

1　实验原理与电路

1.1陶瓷谐振器的等效电路

陶瓷谐振器的电特性在其谐振频率附近可用图1(a)的等效电路表示,电路符号如图1(b)所示[12]。当不振动时,相当于一个平板电容,用C0表示,C0称为静态电容；R为振荡损耗等效电阻；C为弹性等效电容；L为机械振动等效电感。

图1　陶瓷谐振器的等效电路与电路符号

1.2陶瓷谐振器的电抗频率特性

在图1(a)的等效电路中,一般损耗电阻R远小于其他电抗值,故忽略R,得出它的入端电抗为

(1)

式中ω为角频率。

根据谐振的定义,谐振时端口的电压与电流同相,因此谐振时入端阻抗或入端导纳的虚部为零,即公式(1)的分子或分母为零,即:

陶瓷谐振器的串联谐振频率为

(2)

并联谐振频率为

(3)

ωs也就是L、C、R串联谐振回路的谐振频率,此时串联谐振回路的等效阻抗为纯电阻R,因为C0的值很小,它的容抗比电阻R大得多,所以可近似认为在串联谐振时陶瓷谐振器呈纯阻性,且阻抗最小。

当频率高于ωs时,L、C、R串联谐振回路呈感性,与C0构成并联谐振回路,谐振频率就是ωp。由于C≪C0,所以ωp与ωs非常接近。

从上述分析可定性画出陶瓷谐振器的电抗频率特性曲线见图2。图中X=0时ω=ωs是陶瓷谐振器的串联谐振频率,X=∞时ω=ωp是陶瓷谐振器的并联谐振频率。

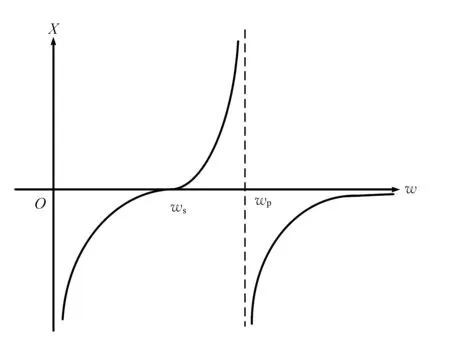
图2　陶瓷谐振器等效电路的电抗频率特性

1.3陶瓷谐振器参数测试方法和电路

陶瓷谐振器在生产过程中,需要对其参数进行测试,根据测试结果进行分类和比较。在实际使用陶瓷谐振器之前,也需要对其进行参数测试,以了解其主要性能。陶瓷谐振器的测试方法有很多[8-11],本文采用一种简单实用的实验方法实现其参数的测试,测试电路见图3。

图3　陶瓷谐振器参数的测试电路

图3中R1为分压电阻,R2为电流取样电阻,一般较小,主要用来调整陶瓷谐振器X串联谐振时的输出电压,使得通过观察vo1与vi同相来测量串联谐振频率更容易些。vi为输入的正弦信号,vo1和vo2均为输出信号(幅值分别为Vo1和Vo2),通过改变输入信号的频率计算该电路的电压增益大小AV1(AV1=Vo1/Vi,Vi为输入信号vi的幅值)和AV2(AV2=Vo2/Vi)即可得到陶瓷谐振器的等效电路参数。

(1) 陶瓷谐振器X串联谐振时的输出信号vo1与输入信号vi同相,且此时的vo1最小,此时的电压增益最小记为Av1min,为

(4)

根据式(4)可求出R。

串联谐振时输入信号的频率记为fs,则有

(5)

(2) 陶瓷谐振器X并联谐振时的输出信号vo2与输入信号vi同相,且此时的vo2最大,并联谐振时输入信号的频率记为fp,则有

(6)

(3) 根据式(5)和式(6),有3个未知量L、C、C0,故还需要至少一组数据或是一个方程式。在图3的测试电路中,电压增益Av2:

(7)

忽略R的Z(w)(见式(1)),将其代入式(7)得到:

(8)

进而根据式(1)、式(5)和式(6),将式(8)变换得到

(9)

从式(9)可以看出,实验中至少测试出一组频率f和Av2的数据,就可以计算出L,然后代入式(5)、式(6),即计算求出C和C0。因此计算L值是关键。本实验利用组合测量法得到L值。在组合测量中,通常测量的次数要远大于待测量的数目,即方程式的个数多于未知量的数目,测量次数多可大大提高测量结果的准确度,因此这里多测几组频率f和Av2的数据代入式(11),该方程式的求解通常借助计算机完成。

2　实验结果与分析

2.1实验结果

实验电路如图3所示。其中R1选用10 kΩ电阻,R2选用100 Ω电阻,X选用日本村田制作的CSB455E型陶瓷谐振器,其振荡频率标称为455 kHz,广泛应用于红外遥控电路中[13]。CSB455E型陶瓷谐振器标称的等效电路参数为常温下L≈7.1 mH、C≈18 pF、C0≈260 pF,R≈7.5 Ω[12]。

实验时,用UT56型数字万用表测得R1=9.984 kΩ,R2=98.35 Ω。输入信号vi为Tektronix AFG310型函数信号发生器产生的幅度为2 000 mV的正弦交流信号。调整该函数信号发生器改变输入信号频率,用AgilentDSO-X 2012A型数字示波器观测输入信号与输出信号的幅度,其中观测输出信号使用的示波器探头型号为Agilent N6862B,接入该探头后的示波器输入阻抗为10 MΩ/15 pF。输入信号频率点选择的一般原则为:离谐振频率点近处取点较多,离谐振频率点远处取点较少。实验测得图3电路的结果如下:

(1) 串联谐振频率fs约为442.0 kHz,此时的vo1与vi同相且最小,幅度约为18 mV,计算得到Av1min≈0.009；

(2) 并联谐振频率fp约为456.7 kHz,此时的vo2与vi同相且最大,幅度约为1 950 mV,电压增益Av2max≈0.975；

(3) 改变输入信号vi的频率,测得对应的输出信号vo2的幅度见表1。

表1　实验数据

2.2计算与分析

根据标称值计算得到的串联谐振频率fs约为445.2 kHz,并联谐振频率fp约为460.4 kHz,实验测得的结果与它们之间的相对误差分别为 0.7%和0.8%。

根据表1的实验数据和公式Av2=Vo2/Vi,计算得到不同频率时的Av2见表2,画出Av2随输入信号频率f变化的曲线见图4中的圆标注的曲线1。

从表1的实验数据可以看出,在并联谐振频率fp附近处Av2大小变化很明显,因此在fp附近取4个频点,分别为:453.0、455.1、456.7、464.0 kHz,分别代入式(11),利用Matlab的非线性最小二乘拟合函数lsqnonlin计算得到陶瓷谐振器的L≈6.9 mH,其余参数也通过Matlab计算得到:C≈19 pF,C0≈277 pF,R≈7.7 Ω。将这些值代入式(9)计算得到不同频率时的Av2记作Av2＇,见表2。Av2＇随输入信号频率f变化的曲线见图4中的正方形标注的曲线2。可以看出,曲线1和2吻合得很好,说明利用组合测量法和Matlab计算的模型可行。

表2　Av2和频率对应的数据列表

表2(续)

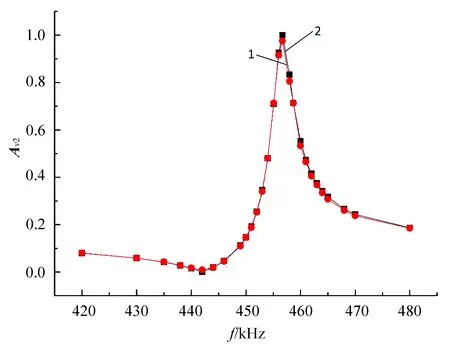
图4　Av2随输入信号频率f变化曲线

实验测得的等效电路参数与厂家标称的等效电路参数也很接近,但存在一些偏差,这主要是由于实际的陶瓷谐振器等效电路参数和厂家标称的等效电路参数存在偏差所致。需要说明的是由于测量时示波器的探头端输入电容约15 pF,因此实验测得的C0值应减去15 pF才是陶瓷谐振器的实际的C0值。

3　结语

文中提出的研究陶瓷谐振器的特性及其测试参数

的实验方法简单实用,对实验仪器的要求较低,该方法也可用于研究其他压电材料和压电器件的特性,比如超声波传感器和石英晶体等。另外该实验研究的内容也非常适用于高校电子电路实验教学中,使学生加深对压电器件特性的理解,引导学生使用组合测量和计算相结合的方法进行实验结果分析等。

References)

[1] 李玲远,田化梅,宋立新. 电子技术基础教程(模拟部分)[M]. 武汉:湖北科学技术出版社,2000:151-152.

[2] 于歆杰,朱桂萍,陆文娟. 电路原理[M]. 北京: 清华大学出版社, 2007:300-303.

[3] 李月国,范坤泰,张录州,等.高频压电陶瓷谐振器的研制[J]. 压电与声光,2001,23(3):183-186.

[4] 范坤泰,朱传琴,张录周,等.片式压电陶瓷谐振器的研制[J]. 压电与声光,2006,28(4):423-425.

[5] 肖洪地,王成建,马洪磊.高频压电陶瓷谐振器的制备与性能[J]. 电子元件与材料,2003,22(1):33-35.

[6] 王红梅,温艳兵,王毅刚. C波段高稳定陶瓷谐振振荡器的设计[J]. 电子设计工程,2011,19(22):101-103.

[7] 蒙延庆. 压电陶瓷换能器的研究与应用[J]. 山东轻工业学院学报,2012,26(3):56-58.

[8] 高龙琴.陶瓷谐振器多参数扫频测试法研究与实现[J]. 仪表技术与传感器,2008(11):81-83.

[9] 于振欢,李东,王艳林.石英晶体自动测试及分选系统设计[J].计算机测量与控制,2011,19(6):1284-1286.

[10] 王晓彦,李东,王艳林.用于石英晶体测试的双通道鉴相系统设计[J].现代电子技术,2015,38(6):133-135.

[11] 袁金库. 基于ARM7的压电陶瓷换能器导纳圆测量仪的研制[D]. 天津:天津大学,2010.

[12] 朱俊鑫. 陶瓷谐振器[J]. 压电与声光,1991,13(6):24-30.

[13] 李北建,傅兴华,何智杰. 红外遥控电路中455kHz陶瓷谐振电路的设计[J]. 电子设计应用, 2005(10):80-82.

Characteristic analysis and parameter measurement of ceramic resonator

Liu Xiaoyan, Lu Yanfeng

(Electronic Engineering Department, Tsinghua University, Beijing 100084, China)

This paper studies the characteristics of ceramic resonator by equivalent circuit model and measurement of the equivalent circuit parameters by the combined measurement method. The experimental results show that the method is not only feasible, but also simple and practical.College circuit laboratories are generally equipped with the experimental instruments. The method can be used for understanding the characteristics of ceramic resonator, the CAD simulation of the circuit, and testing of the characteristic parameters of piezoelectric materials and components.In addition, the content of this experiment is very suitable for the experimental teaching of electronic circuits in colleges.

ceramic resonator; equivalent circuit parameters; combined measurement method; Matlab calculation

DOI:10.16791/j.cnki.sjg.2016.04.013

2015- 09- 02修改日期：2016- 01- 19

刘小艳(1983—),女,湖南衡阳,硕士,工程师,主要从事电子电路方面的实验教学和科研.

E-mail：xyl@tsinghua.edu.cn

TN710

A

1002-4956(2016)4- 0046- 04