灌区重力式挡土墙初始应力作用有限元分析

孔维龙（中国市政工程西北设计研究员有限公司，甘肃　兰州730000）

灌区重力式挡土墙初始应力作用有限元分析

孔维龙
（中国市政工程西北设计研究员有限公司，甘肃兰州730000）

近年来我国修建工程的区域范围越来越大，遇到的工程问题也越来越多，特别是在灌区修建重力式挡土墙的初始应力作用下的变形问题，一直是困扰工程进度的难题。本文利用有限元软件ADINA针对昌马灌区某一重力式挡土墙在重力作用下的初始变形进行了分析。结果表明：基于瞬态重力作用下ADINA的数值模拟可知，重力作用下由于地基反力的作用使得挡土墙的竖直方向z的应力（σ）与变形（D）都大于水平向y这与实际是一致的。

重力式挡土墙；应变；有限元；ADINA

伴随着我国经济的不断发展，灌区规模的不断扩大，土地利用效率越来越高，特别是在河西走廊地区，当灌区渠线遇到小的山包时，往往需要挡土墙去支护，这使得挡土墙在重力作用下的初始应力变形问题成为困扰着工程健康发展的难题。

挡土墙的分类方法很多，一般的结构形式主要有三种：重力式、悬臂式和扶壁式。其中重力式挡土墙由于其施工方法简单，施工效率高而被广泛的运用。本文利用有限元软件ADINA针对昌马灌区某一重力式挡土墙在重力作用下的初始变形进行了分析，从而为以后的灌区挡土墙设计提供科学经济有效的方法［1～3］。

1　有限元理论模型与方法

随着计算机技术的发展，有限单元法成为现在解决工程问题的主流，有限元法主要是将分析域进行离散化处理，然后根据变分原理将力学分析中的控制方程基边界条件转化为等效的代数方程组，从而确定求解域内连续的场函数问题转化为求解有限各离散点处的场函数值问题。有限元法概括起来包括以下六个步骤：

（1）连续体的离散化［4］。离散化即是将给定的连续体分割成等价的有限单元组合，单元体只有在结点处相互连接，构成一个单元的集合体，用以代替原来的结构。

（2）选择位移模式［5］。对单元中位移的分布做出一定的假定，假定位移是坐标的某种简单的函数，即位移模式，就可以导出用结点位移表示单元内任一点位移的关系式，其矩阵形式是：

式中：｛f｝—单云内任一点位移列阵；

｛δ｝ε—单元的结点位移列阵；

［N］—形函数矩阵，它的元素是结点位置坐标的函数。

（3）利用变分法（或虚功原理）推导单元刚度矩阵，根据几何方程，由位移的表达式（1）导出用结点位移表示单元应变的关系式

式中：｛ε｝—单元内任一点位移列阵；

［B］—单云应变矩阵。

再根据物理方程，由应变表达式（2）导出用结点位移表示单元应力的关系式：

式中：｛σ｝—单元内任一点应力列阵；

［D］—与单元材料有关的弹性矩阵。

根据变分原理，建立作用于单元上的结点力与结点位移之间的关系，即单元的平衡方程，即可得到单元的刚度矩阵

式中：［δ］e—单元刚度矩阵；

｛F｝e—单元结点力列阵。

（4）计算等效结点荷载［6］。利用虚工原理，将作用在单元上的边界力、表面力以及体积力等转换为等效节点荷载加到节点上。

（5）进行整体分析，综合整个离散化连续体的代数体的代数方程式组，建立平衡方程将各个单元的刚度矩阵集合成整个结构的整体刚度矩阵［k］；再将作用于各单元的等效结点力列阵集合成总的荷载列阵［k］。通过集合所有单元的平衡方程得到整体平衡方程：

式中：［k］—整体刚度矩阵；

［δ］—整体结点位移列阵；

｛F｝—整体荷载列阵。

（6）求解。通过求解整体平衡方程得出结点位移，并根据以上应变、应力与结点位移之间的关系分别得出相应的结果。

3　实例分析

本文以甘肃昌马灌区某一重力式挡土墙为研究对象，对其在重力作用下的初始变形进行数值模拟仿真计算。

3.1工程的基本资料及有限元模型的建立

昌马灌区渠道重力式挡土墙有限元模型如图1所示。

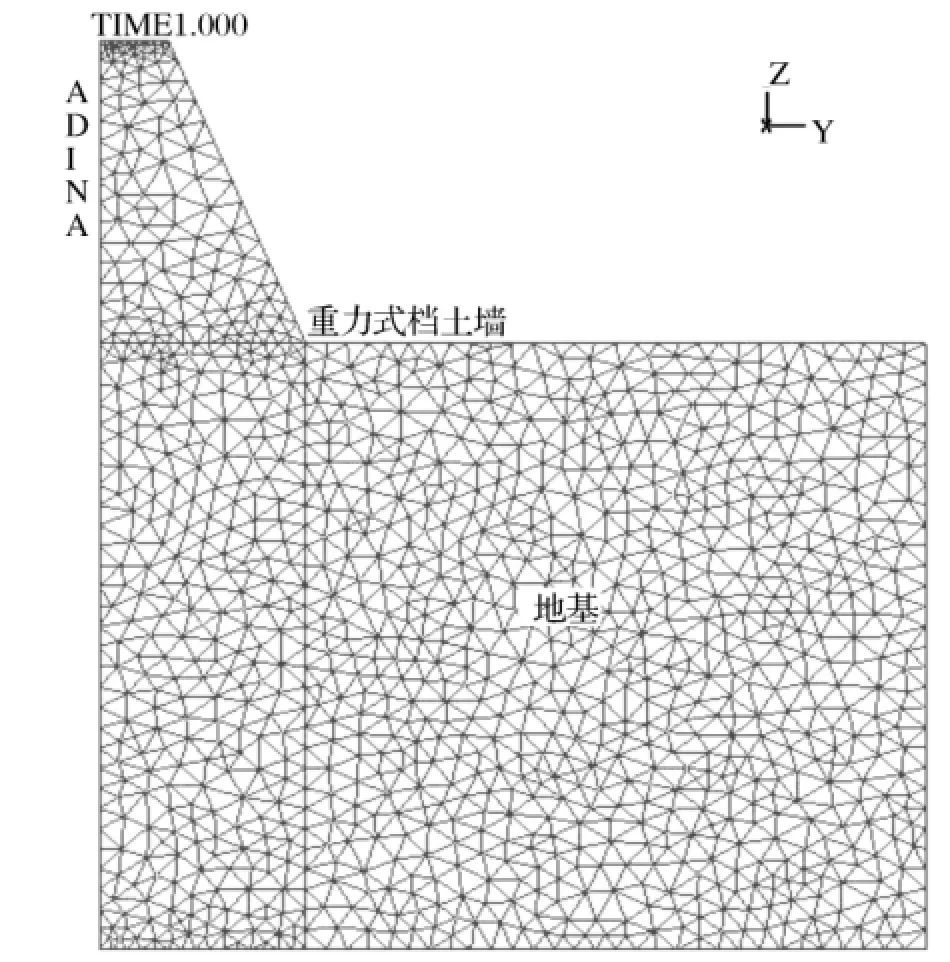
图1　重力式挡土墙有限元模型

挡土墙采用C25素混凝土浇筑，其中相关材料参数表，见表1：

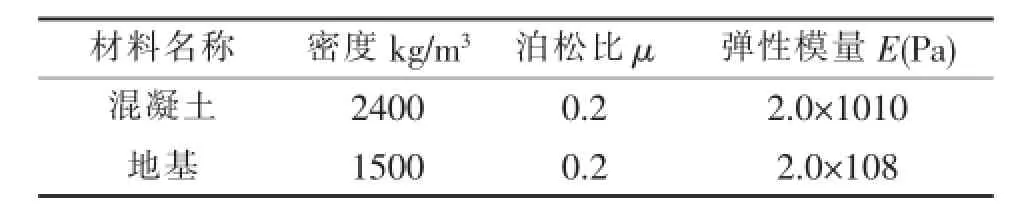
表1　相关材料力学参数表

4　重力作用下挡土墙初始应力应变模拟及数值模拟结果分析

4.1重力作用下初始位移（D）有限元分析结果

从图2、图3中可以看出在重力的作用下，重力式挡土墙y方向变形很小，其中Dymax=1.1mm，但是由于地基的限制以及重力式挡土墙自身的重力作用，其z向的变形较大，Dzmax=30mm这与实际是相符合的。

图2　挡土墙Dy向变形等值线图

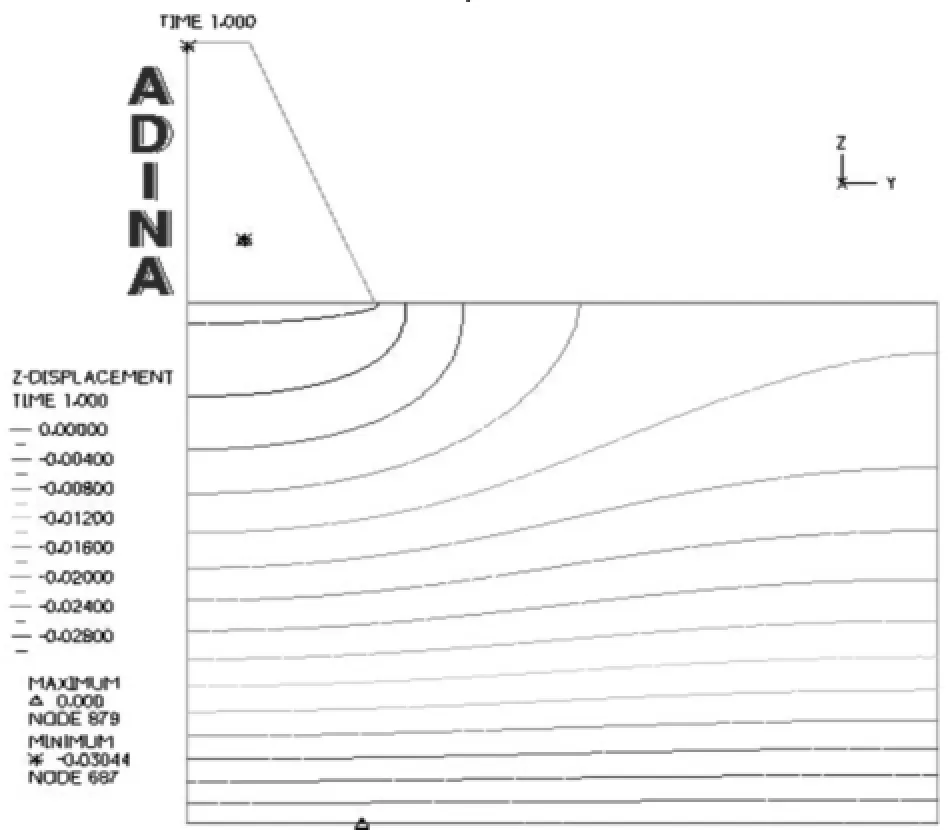
图3　挡土墙Dz向变形等值线图

图4　挡土墙σy身应力等值线图

图5　挡土墙σz向应力等值线图

4.2初始应力（σ）有限元分析结果

从图4、图5中可以看出在重力的作用下，重力式挡土墙y方向应力较小，其中σymax=1.4MPa，但是由于地基的限制以及重力式挡土墙自身的重力作用，其z向的应力较大，σzmax=1.9MPa，且其最大应力出现在墙角处，这与实际是相符合的。

6　结论

（1）基于瞬态重力作用下ADINA的数值模拟可知，重力作用下由于地基反力的作用使得挡土墙的竖直方向z的应力（σ）与变形（D）都大于水平向y这与实际是一致的。

（2）通过有限元软件分析出了重力作用下的挡土墙变形的各个方向的变形与应力为以后的工程实践提供理论依据。

（3）通过有限元软件模拟分析得出，地基的限制以及重力式挡土墙自身的重力作用，其z向的应力较大，σzmax=1.9MPa且其最大应力出现在墙角处，这与实际是相符合的。

［1］李磊.水工钢筋混凝土结构［M］.北京：水利电力出版社，1975.

［2］王元占，王海龙，张文忠.挡土墙压力分布［J］.中国港湾建设.2000（4）：1-5.

［3］胡玉银.挡土墙抗倾覆稳定性分析［J］.同济大学学报，1995（3）.

TV476+.4