页岩储层复杂裂缝扩展研究

潘林华，张烨，陆朝晖，邓智，柳凯誉（1.国土资源部页岩气资源勘查重点实验室（重庆地质矿产研究院），重庆 400042；2.重庆市页岩气资源与勘查工程技术研究中心（重庆地质矿产研究院），重庆 400042；.中国石油集团公司长城钻探公司井下作业分公司，辽宁 盘锦 124000）



页岩储层复杂裂缝扩展研究

潘林华1，2，张烨1，2，陆朝晖1，2，邓智1，2，柳凯誉3
（1.国土资源部页岩气资源勘查重点实验室（重庆地质矿产研究院），重庆 400042；2.重庆市页岩气资源与勘查工程技术研究中心（重庆地质矿产研究院），重庆 400042；3.中国石油集团公司长城钻探公司井下作业分公司，辽宁 盘锦 124000）

页岩储层孔隙度和渗透率低，岩石脆性大，天然裂缝发育。大规模水力压裂过程中，页岩储层易发生张性破坏和剪切破坏相结合的复合破坏，形成复杂网状裂缝，而网状裂缝的展布形态关系到页岩压裂方案的设计和压后产能的评估。针对页岩储层网状裂缝扩展问题，基于流-固耦合方程和损伤力学原理，建立了二维网状裂缝扩展有限元模型。综合研究认为：水平主应力差增大，压裂裂缝分布长度增加，分布宽度降低，长宽比增大；压裂施工排量降低，压裂裂缝复杂程度降低，压裂裂缝分支数减少，分布长度增加，分布宽度降低，长宽比增大；水平井“多段分簇”压裂可能出现多裂缝干扰问题，部分压裂裂缝在延伸过程中止裂或者沟通两端射孔簇的压裂裂缝；水平井“多段分簇”压裂过程中，各个射孔簇形成的压裂裂缝分支长度差别较大，部分裂缝分支长度明显大于其他裂缝分支。

页岩气；天然裂缝；裂缝扩展；网状裂缝；损伤力学；有限元

0　引言

四川盆地富含泥页岩，且分布广泛，页岩气资源潜力巨大［1-4］。重庆地区是页岩气勘探开发的主战场之一，目前，涪陵、黔江、城口、秀山等区块正在进行勘探开发。其中，中石化涪陵页岩储层由于其独特的地质构造和储层特性［5-7］，已经成为我国页岩气勘探与开发的主要示范区。重庆地区页岩储层埋深在500～4 000 m，水平井“多段分簇”压裂是主要的压裂增产模式，部分勘探井或者极浅的页岩气开发井采用直井压裂进行产能评估和预测。页岩储层脆性矿物体积分数高，岩石脆性大，天然裂缝发育，压裂过程中，可能发生张性破坏和剪切破坏相结合的混合破坏［8］，从而导致复杂网状裂缝的形成，而网状裂缝的展布形态直接关系到页岩储层压裂施工方案的制定与压后产能评估。因此，压裂裂缝的形态确定，对于水力压裂至关重要。

常规压裂裂缝扩展模拟方面已经进行了大量研究，形成了许多裂缝扩展模型，但常规的裂缝扩展模型不适用于页岩复杂裂缝扩展。对于复杂裂缝扩展，国外也已进行了多种模拟方法的研究［8-10］，而国内对复杂裂缝扩展的研究相对较少，总体处于探索阶段［11-12］。目前，裂缝扩展数值模拟最主要的有5种方法：1）常规有限元法。主要利用损伤力学原理进行裂缝扩展模拟，包括预设黏结单元法［13］和材料属性动态改变法［14］。其中，后者利用损伤准则，适时改变材料单元属性以模拟裂缝扩展，计算精度易受单元尺寸的影响，但处理复杂裂缝扩展问题比较方便。2）扩展有限元法［15］。将天然裂缝和压裂裂缝的表征独立于计算网格外，利用位移不连续函数表征裂缝特征。该方法模拟精度高，裂缝处理方便，但裂缝条数过多时，计算速度慢，收敛性较差。3）边界元法［16］。处理裂缝随机扩展有一定的优势，但处理流-固耦合问题时存在一定的难度。4）无单元法［17］。计算过程中不需要网格划分，利用任意分布的坐标点构造控制方程，模拟复杂裂缝扩展方便，但成熟性和稳定性有待加强，计算效率有待提高。5）解析模型解法［10］。根据应力-应变关系，构建裂缝扩展的判断解析公式，模拟方法精度低。

本文以重庆地区页岩储层作为主要研究对象，根据损伤力学的基本原理，考虑流-固耦合算法，采用动态改变单元的材料属性模拟裂缝扩展，对页岩储层复杂网状裂缝扩展机理进行了研究，分析了水平主应力差和施工排量等对网状裂缝展布形态和展布特征的影响。

1　裂缝扩展模型

1.1裂缝扩展平衡方程

基于Biot理论，考虑流体流动方程、基质几何方程及连续性方程（流体和基质），可以获得流-固耦合的控制方程。流体和基质的平衡方程［18］分别为

式中：φ为孔隙度，无因次；Ct为基质压缩系数，1/Pa；p为孔隙压力，Pa；α为Biot系数；u为位移张量，m；t为压裂液注入时间，s；K为渗透率，10-3μm2；μ为液体黏度，Pa·s；λ，G均为拉梅常量；xi为节点坐标，m。

1.2本构方程

页岩储层脆性大，失效前塑性变形小。本文将页岩储层假设为线弹性材料，模拟过程中不考虑塑性变形作用。应力-应变关系式［19］为

式中：σ为应力张量，Pa；E0为页岩初始弹性模量，Pa；ε为应变张量，无因次。

存在损伤的基质、压裂裂缝和天然裂缝的本构关系［20］：

式中：D为损伤变量，无因次；E（1-D）为损伤单元的弹性模量，Pa。

将天然裂缝视为损伤材料［21］，在本文的模拟中，天然裂缝的初始损伤值设定为0.5，天然裂缝的弹性模量设为基质单元的0.5倍，渗透率根据参考文献［22-23］中的公式进行计算。

1.3渗透率-应力-损伤耦合方程

对天然裂缝和压裂裂缝，本文参考文献［22-23］中的处理方法。这主要基于以下3点：1）裂缝的形成方式相同，流体压力导致裂缝失效；2）本构模型基于脆弹性理论；3）破坏方式相近，拉伸破坏和摩尔-库伦剪切破坏共同决定裂缝的扩展。

本文对裂缝失效的判断，主要依据拉伸失效准则和摩尔-库伦失效准则，渗透率-应力-损伤的耦合方程的具体处理方式参照文献［22-23］。

1.4裂缝损伤单元处理方法

利用损伤力学原理进行复杂裂缝形态模拟，国内外学者进行了大量的探索和研究。文献［21］研究了单条水力裂缝遇到天然裂缝后的裂缝转向情况，定义了天然裂缝单元和水力压裂裂缝损伤单元的力学参数的取值，但是没有考虑损伤单元的渗透率动态变化问题。文献［14，19-20］利用损伤力学原理进行了渗流-应力-损伤条件下的裂缝扩展模拟。模型考虑了力学参数和渗透率的弱化，可以进行压裂裂缝扩展模拟，但是裂缝的损伤主要还是通过液体压力或者应力控制，没有实现液体流量控制条件下的裂缝损伤扩展，与现场水力压裂过程存在一定的差别。本文综合了上述模型的处理方法，模拟过程中，所有单元均采用相同的单元类型，对天然裂缝、压裂裂缝流体单元采用不同的材料属性。天然裂缝单元的弹性模量较基质低，泊松比、孔隙度、渗透率较基质单元高，压裂裂缝流体单元孔隙度、渗透率极高，泊松比接近0.5，弹性模量较低。为此，本文利用流量进行孔隙压力控制，使模拟过程更加接近真实的水力压裂过程。

1.5模型的求解

根据流-固耦合基本方程，考虑模型的初始条件和边界条件，利用有限元法对控制方程进行离散，形成方程矩阵，最后进行求解。矩阵求解过程中，将应力-应变和渗流划分成2个独立系统，分别进行迭代求解。根据裂缝失效判断准则，适时改变单元的材料属性。

2　数值模型的建立

本文数值模型的建立，主要参考国内外相应模型的处理方法，对于损伤单元，进行了力学参数的弱化和渗透率的增强。为了更加接近现场的水力压裂过程，本文模型采用注入流量进行压力控制。为了保证模型的精度，本文的模型对裂缝可能存在的区域进行了网格加密，每个计算模型的网格数在50×104～80×104。

根据重庆地区部分页岩气井的水力压裂微地震解释结果，垂直井的水力裂缝长度一般小于200 m，水平井“多段分簇”压裂的最大裂缝长度一般小于300 m。因此，本文的计算模型中，垂直井模型的长度和宽度取200 m，水平井模型长度和宽度取300 m。根据重庆地区某水平井储层实际情况，对水平井“多段分簇”射孔压裂中的1个压裂段进行模拟，模拟射孔段的长度为100 m，共4簇射孔。垂直井压裂的计算模型如图1a所示，水平井“多段分簇”压裂的计算模型如图1b所示。射孔端附近边界采用对称位移、不渗透边界，其他的边界采用位移、孔压边界。

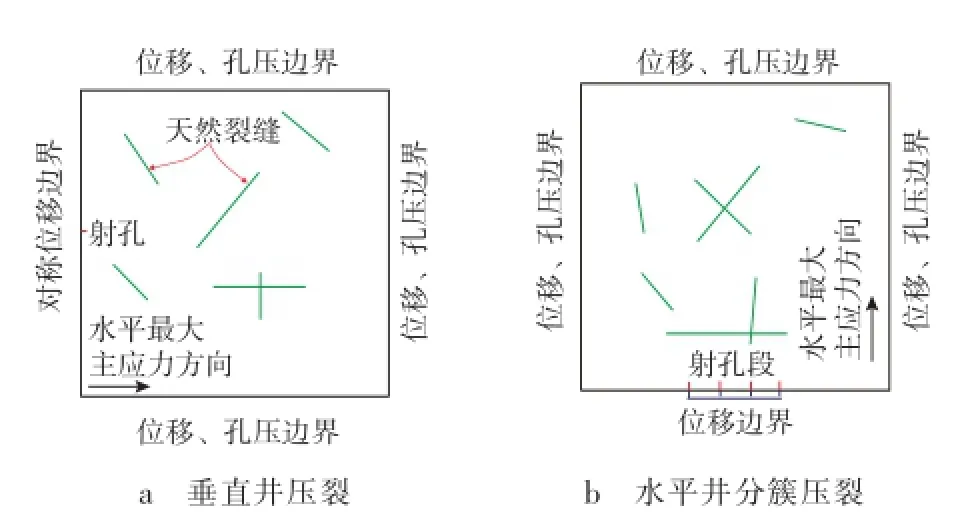
图1　计算模型示意

数值模型的计算参数主要通过室内实验和现场施工获得（见表1）。为了研究某些参数对页岩裂缝扩展的影响，后续的模拟过程中部分参数可能发生改变。

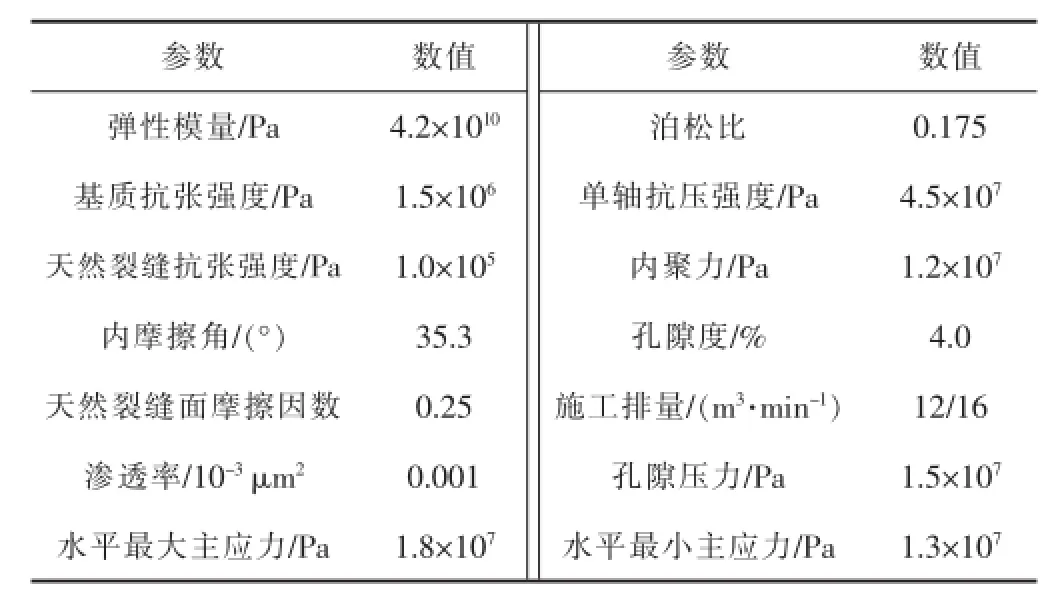
表1　模拟过程选取的计算参数

3　水力压裂裂缝扩展模拟结果

页岩水力压裂裂缝的复杂程度受储层地质条件（如水平主应力差）和施工参数（压裂液量、施工排量）的共同影响。本文主要考虑水平主应力差、压裂施工排量对页岩储层水力压裂体积裂缝扩展的影响。

3.1水平主应力差对网状裂缝的影响

利用所建立的页岩复杂裂缝扩展模型，进行了一系列不同水平主应力差条件下的裂缝扩展模拟，可以获得相应条件下的复杂裂缝形态和展布情况（见图2）。

图2　垂直井和水平井的天然裂缝分布和裂缝扩展结果

垂直井和水平井压裂模拟的天然裂缝分布形态如图2a，2c所示。在此天然裂缝分布条件下，水平主应力差为5 MPa时的垂直井裂缝扩展结果如图2b所示。压裂过程中，压裂裂缝形成了2个明显的主裂缝分支，近井筒附近形成了网状裂缝。水平主应力差为5 MPa时，水平井“多段分簇”压裂的裂缝扩展结果如图2d所示。压裂过程中，各个射孔簇形成了压裂裂缝的长度差别较大，两端的射孔簇形成了2个主要的压裂裂缝分支，中间射孔簇形成的压裂裂缝长度较小。

不同水平主应力差条件下，水平井“多段分簇”压裂的裂缝扩展形态和裂缝参数见图3。

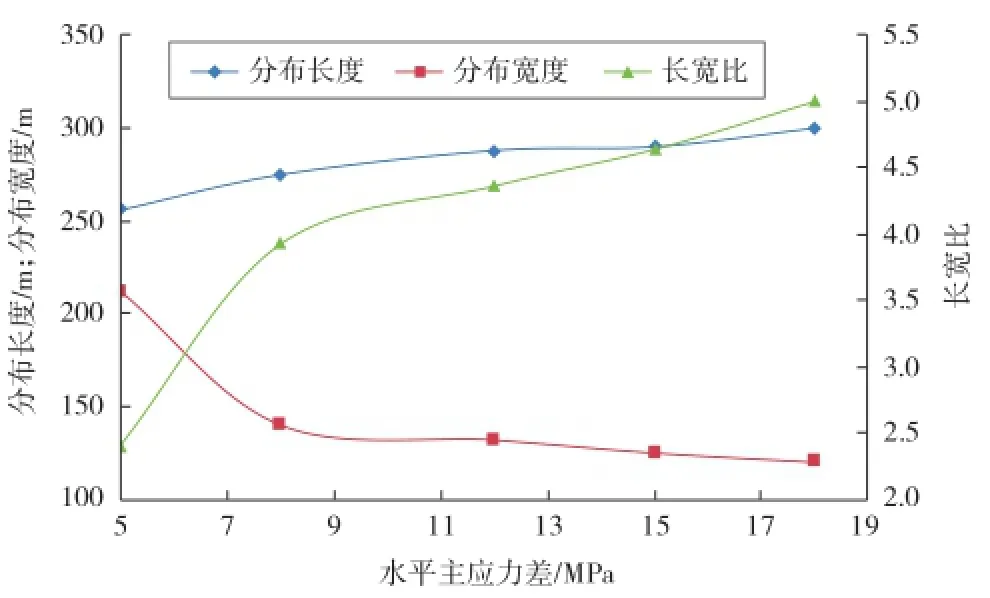
图3　不同水平主应力差条件下的裂缝展布情况

由图3可知：施工液量相同，水平主应力差增大，压裂裂缝的分布长度增加，但分布宽度降低，压裂裂缝的长宽比（长宽比=2×分布长度/分布宽度）增大。此种情况下，主裂缝分支周围的小裂缝分支较多，中间射孔簇形成的压裂裂缝延伸距离较短，近井筒附近形成了网状裂缝。

不同水平主应力差条件下，垂直井压裂的裂缝形态和展布特征与水平井压裂裂缝形态具有类似的规律。

3.2施工排量对网状裂缝的影响

水平主应力差5 MPa、不同施工排量条件下，垂直井水力压裂和水平井“多段分簇”压裂过程中形成的压裂裂缝的分布形态和长宽比如图4所示。由图4a可以看出：垂直井水力压裂中，施工排量降低，压裂裂缝复杂程度明显降低，分支数减少，分布长度增加，分布宽度降低，长宽比增加。由图4b可以看出：水平井“多段分簇”压裂中，施工总液量相同，施工排量降低，裂缝的分布长度增加，分布宽度降低，长宽比增加。

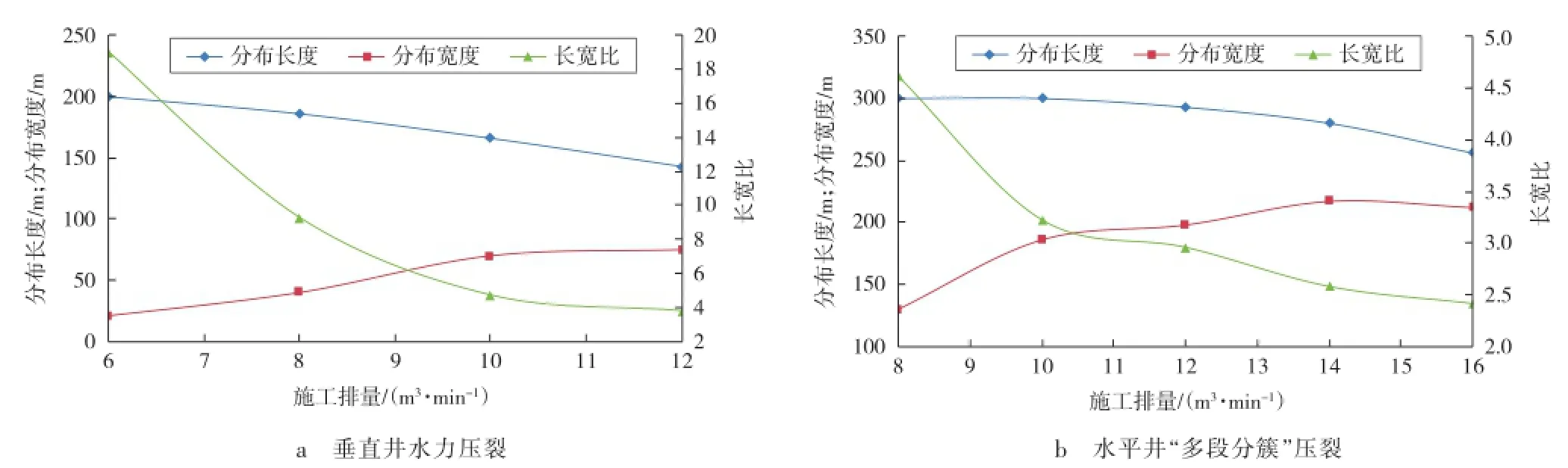
图4　不同施工排量条件下的裂缝展布结果

3.3水平井“多段分簇”压裂多裂缝干扰

水平井“多段分簇”射孔压裂过程中，各个射孔簇之间可能发生干扰现象，中间射孔位置的裂缝延伸过程中可能发生止裂，也有可能发生转向，裂缝连通两端射孔压裂裂缝。

不同水平主应力差条件下，水平井“多段分簇”压裂4个射孔簇形成的裂缝长度见表2。

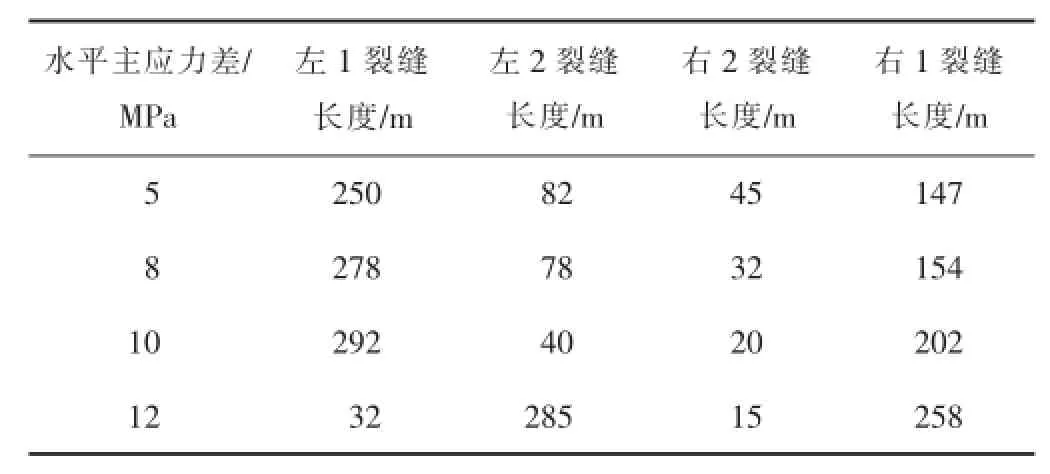
表2　不同水平主应力差下4个射孔簇形成的裂缝长度

表2中“左1裂缝”表示的是4簇射孔中最左端的射孔形成的裂缝，其他依此类推。由表2可以发现：施工排量和施工液量相同、水平主应力差不同时，4簇射孔形成的压裂裂缝长度差异较大；除了水平主应力差为12 MPa时，左2裂缝成为压裂主裂缝以外，其他条件下所有压裂主裂缝分支均为两端的射孔簇形成的裂缝，中间射孔簇形成的裂缝长度相对较小且容易发生转向，沟通两端射孔簇形成的裂缝；同时，压裂过程中形成的多个主裂缝分支长度差别较大，某一主分支裂缝的长度明显大于其他裂缝分支。

4　结论

1）基于流-固耦合基本方程和损伤力学原理，建立了页岩复杂裂缝扩展模型，研究了页岩复杂裂缝扩展规律。

2）水平主应力差增大，压裂裂缝的分布长度增加，分布宽度降低，长宽比增大。

3）施工排量降低，压裂裂缝复杂程度降低，压裂裂缝的分支数减少，分布长度增加，分布宽度降低，长宽比增加。

4）水平井“多段分簇”射孔压裂可能造成多裂缝干扰，部分裂缝在延伸过程中止裂或者沟通两端射孔簇的压裂裂缝。

5）水平井“多段分簇”压裂过程中，各个射孔簇形成的压裂裂缝分支长度差别较大，某一主分支裂缝的长度明显大于其他裂缝分支。

［1］罗健，戴鸿鸣，邵隆坎，等.四川盆地下古生界页岩气资源前景预测［J］.岩性油气藏，2012，24（4）：70-74.

［2］黄籍中.四川盆地页岩气与煤层气勘探前景分析［J］.岩性油气藏，2009，21（2）：116-120.

［3］余川，程礼军，曾春林，等.渝东北地区下古生界页岩含气性主控因素分析［J］.断块油气田，2014，21（3）：296-300.

［4］梁榜，何生，陈学辉，等.鄂西渝东地区东岳庙段页岩气勘探潜力研究［J］.断块油气田，2015，22（1）：36-41.

［5］周德华，焦方正，郭旭升，等.川东南涪陵地区下侏罗统页岩油气地质特征［J］.石油与天然气地质，2013，34（4）：450-454.

［6］王志刚.涪陵页岩气勘探开发重大突破与启示［J］.石油与天然气地质，2015，36（1）：1-6.

［7］尹俊，严文芬，林琳.涪陵地区大安寨段优质泥页岩地震预测［J］.断块油气田，2015，22（3）：334-337.

［8］Olson J，Taleghan A D.Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures［R］. SPE 119739，2009.

［9］ Cipolla C，Weng X，Ganguly U，et al.Integrating microseismic mapping and complex fracture modeling to characterize fracture complexity［R］. SPE 140185，2011.

［10］Weng X，Kresse O，Cohen C，et al.Modeling of hydraulic fracture network propagation in a naturally fractured formation［J］.SPE Journal，2011，26（4）：368-380.

［11］翁定为，雷群，胥云，等.缝网压裂技术及其应用［J］.石油学报，2011，32（2）：280-284.

［12］吴奇，胥云，王腾飞，等.增产改造理念的重大变革：体积改造技术概论［J］.天然气工业，2011，31（4）：7-12.

［13］张广明，刘合，张劲，等.储层流固耦合的数学模型和非线性有限元方程［J］.岩土力学，2010，31（5）：1657-1662.

［14］李林地，张士诚，张劲，等.缝洞型碳酸盐岩储层水力裂缝扩展机理［J］.石油学报，2009，30（4）：571-573.

［15］Belytschko T.Elastic crack growth in finite elements with minimal remeshing［J］.International Journal for Numerical Methods in Engineering，1999，45（5）：601-620.

［16］Olson J.Multi-fracture propagation modeling：Applications to hydraulic fracturing in shales and tight gas sands［R］.ARMA 08-327，2008.

［17］Moes N，Dolbow J，Belytschko T.A finite element method for crack growth without remeshing［J］.International Journal for Numerical Methods Engineering，1999，46（1）：131-150.

［18］Chen H Y，Teufel L W，Lee R L.Coupled fluid flow and geomechanics in reservoir study-I.Theory and governing equations［R］.SPE 30752，1995.

［19］杨天鸿，屠晓利，於斌，等.岩石破裂与渗流耦合过程细观力学模型［J］.固体力学学报，2005，26（3）：333-337.

［20］杨天鸿.岩石破裂过程渗透性质及其与应力耦合作用研究［D］.沈阳：东北大学，2001.

［21］Rahman M，Aghighi M，Rahman S，et al.Interaction between induced hydraulic fracture and pre-existing natural fracture in a poro-elastic environment：Effect of pore pressure change and the orientation of natural fracture［R］.SPE 122574，2009.

［22］李连崇，杨天鸿，唐春安，等.岩石水压致裂过程中的耦合分析［J］.岩石力学与工程学报，2003，22（7）：1060-1066.

［23］潘林华，程礼军，张士诚，等.页岩储层体积压裂裂缝扩展机制研究［J］.岩土力学，2015，36（1）：205-211.

（编辑李宗华）

Complex fracture propagation in shale gas reservoir

Pan Linhua1，2，Zhang Ye1，2，Lu Zhaohui1，2，Deng Zhi1，2，Liu Kaiyu3
（1.MLR Key Laboratory of Shale Gas Exploration，Chongqing Institute of Geology and Mineral Resources，Chongqing 400042，China；2.Chongqing Engineering Research Center for Shale Gas Resource&Exploration，Chongqing Institute of Geology and Mineral Resources，Chongqing 400042，China；3.Downhole Operation Company of Great Wall Drilling Company，CNPC，Panjin 124000，China）

Combination of tensile failure and shear failure is liable to occur in shale reservoir rock，which will generate complex network fractures in the process of large scale hydraulic fracture，because of the low porosity and permeability，high brittleness and massive natural fractures.Distributing features and fracture geometry of network fracture are related to the design of hydraulic fracturing scheme and the after fracturing productivity prediction.In order to investigate the propagation process of complex fracture network，a two dimensional finite element model is built based on fluid-solid coupling equations in porous medium and theory of damage mechanics.The comprehensive evaluation shows that:the distribution length of network fracture will increase while the distribution width decreases with the increase of the horizontal stress difference，which means the distribution length to width ratio of the network fracture will increase；as the pump rate decreases，the distribution length and the length to width ratio will increase，but the branches，fracture complexity and distribution width will decrease；fractures interference will occur in the process of multiple clusters staged horizontal well，partial fracturing fractures of some perforation clusters will stop propagating or connect the fractures of both ends perforation clusters；there is a great difference in the fracture length of hydraulic fracture generated from every perforation cluster，and the branches of some fractures are much longer than those of the other branches.

shale gas；natural fracture；fracture propagation；network fracture；damage mechanics；finite element method

国家自然科学基金项目“页岩气储层低频脉冲水力压裂增渗机理研究”（51304258）；重庆市基础与前沿研究计划项目“页岩气储层低频脉冲水力压裂增渗机理研究”（cstc2013jjB90005）；重庆市国土局科研项目“重庆市页岩气勘探有利区带优选及资源量评价研究”

TE122.2+3

A

10.6056/dkyqt201601020

2015-07-26；改回日期：2015-11-16。

潘林华，男，1982年生，工程师，博士，主要从事岩石力学、地应力和压裂裂缝起裂和扩展等方面的研究工作。电话：023-88316034；E-mail：plh_cup@163.com。

引用格式：潘林华，张烨，陆朝晖，等.页岩储层复杂裂缝扩展研究［J］.断块油气田，2016，23（1）：90-94.

Pan Linhua，Zhang Ye，Lu Zhaohui，et al.Complex fracture propagation in shale gas reservoir［J］.Fault-Block Oil&Gas Field，2016，23（1）：90-94.