基于遗忘因子多新息随机梯度算法PMSM参数辨识

张建宇，吴定会

(江南大学 轻工过程先进控制教育部重点实验室,无锡 214122)

基于遗忘因子多新息随机梯度算法PMSM参数辨识

张建宇，吴定会

(江南大学 轻工过程先进控制教育部重点实验室,无锡 214122)

针对传统辨识算法结果不精确以及电机参数变化问题，提出了基于遗忘因子多新息随机梯度辨识算法。结合永磁同步电机系统电压方程，构建离散辨识模型。采用矢量控制方法控制电机，获得辨识模型输入输出数据，对转子电阻和电感参数进行在线辨识。仿真结果表明，该算法能够实现对永磁同步电机参数的辨识。

永磁同步电机；SVPWM矢量控制；遗忘因子；多新息随机梯度算法；参数辨识

0 引 言

永磁同步电机具有结构简单、安全可靠等优点、在伺服控制、风力发电等很多领域得到广泛应用[1]。在众多永磁同步电机控制方法中比较成熟的是矢量控制方法，矢量控制模型有电流环和速度环两个闭环回路，通过设定两个回路控制器的参数控制电机运行，控制器参数设定需要精确的电机参数(电阻和电感)。同时其他的控制策略，如直接转矩控制、弱磁控制、自适应控制等，也都离不开精确的参数[2-4]，然而永磁同步电机自身和周围环境的变化导致的参数不确定性以及模型中各参数之间的强耦合性导致控制算法不精确。为了得到精确的电机参数来更好控制电机的运行，需要找到合适的参数辨识算法进行参数辨识。

参数辨识分为离线辨识和在线辨识，在线辨识是对实时采集数据通过所采用的算法进行辨识，相对于离线辨识有实时性的优点。例如，递推最小二乘算法、随机梯度算法等都是在线辨识[5-7]。文献[5]将正交投影和递推最小二乘相结合对永磁同步电机参数在线辨识；文献[6]提出基于双滑模模型参考自适应系统构建两个滑模面,并通过滑模算法在线辨识转子速度和转子位置角度；文献[7]将神经网络与扩展卡尔曼滤波算法结合进行参数辨识。以上几种算法在提高辨识精度的同时，也存在一些缺点：比如增加了计算量或者损失了收敛速度等。如随机梯度算法的运算数据为标量，不用计算协方差阵，具有计算量小的优势，但同时它的缺点是收敛速度比较慢。将多新息理论与传统算法相结合得到新的辨识算法在一定程度上解决了这些问题，文献[8]研究了多新息最小二乘算法，限定了数据长度，不会出现数据大量累积的情况；文献[9-10]分析了多新息随机梯度算法，相对于随机梯度算法，增加了每次计算对数据的利用率，在减小计算量的同时又提高了收敛速度；文献[11]是将多新息随机梯度算法与神经网络结合进行研究。

永磁同步电机因其安全可靠，经常工作在比较恶劣环境中，电机参数很容易受到环境的影响，所以辨识算法除了能够精确辨识固定参数之外还必须具备实时和快速的特点来应对参数的变化。多新息随机梯度算法一方面能够通过设置新息长度随时舍弃旧数据，同时有很好的收敛速度和收敛精度，适合作为永磁同步电机参数固定和时变两种情况辨识的算法。

本文结合永磁同步电机d-q轴旋转坐标系下的系统电压数学模型构建离散回归模型，采用SVPWM矢量控制方法进行控制并采集数据，利用遗忘因子多新息随机梯度算法编写的在线辨识模块进行参数辨识。根据仿真实验得出的结论，遗忘因子多新息随机梯度算法对永磁同步电机的参数辨识在收敛速度和精度上都优于随机梯度算法，并逐渐增加新息长度P，其辨识效果逐渐接近递推最小二乘算法。

1 遗忘因子多新息随机梯度算法

对于下面线性回归模型：

式(1)中，v(t)∈R1为噪声向量。

根据梯度搜索原理极小化J(θ)得到式(2)～式(4)随机梯度算法(SG)：

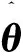
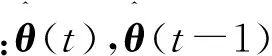
与最小二乘算法相比，随机梯度算法不需要计算协方差阵，大大减小了计算量，但是随机梯度算法的缺点是仅使用了当前时刻的数据，由于数据利用率低，所以存在收敛速度慢和收敛精度不精确的缺点，为了改善以上缺点，就要增加每次计算对数据的利用率，引入新息长度p，即增加数据长度，将原来的单新息量e(t)扩展到数据长度为p的多新息向量得[9-10]：

式中：y(t-i),φ(t-i)，i=1,2，...,p-1表示过去时刻的值。式(5)可以表示：

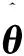
根据随机梯度算法得到多新息随机梯度算法(Multi-Innovation Stochastic Gradient Algorithm,MISG)：

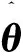
当新息长度p=1时，就变为随机梯度算法，所以多新息随机梯度算法是随机梯度算法的推广。相对于随机梯度算法和最小二乘算法，多新息随机梯度算法可以设定一定的数据长度p，既可以使数据得到比较充分的利用，又能避免最小二乘算法中的大计算量，是两种算法的折中。多新息随机梯度算法收敛性证明可参考文献[12]。

实际应用中，多新息随机梯度算法的收敛速度和精度并不十分理想，所以加入遗忘因子FF来提高收敛速度和精度，便得到遗忘因子多新息随机梯度算法，即将式(9)修改为式(10)：

2 永磁同步电机的数学模型

永磁同步电机转子中通过嵌入永磁体产生稳定的磁场，不需要外加励磁电流产生感应磁场，从而使电机模型大大简化。定子侧是三相对称的定子绕组，通过在定子侧通入三相对称电流产生旋转磁场与转子磁场相互作用产生电磁转矩实现转子的转动。

为了更方便的控制电机运转，忽略一些影响不大的因素，比如定子铁心饱和、永磁体的阻尼作用等情况。并将在此基础上建立的永磁同步电机的数学模型等效变换为直流电机形式的模型，即将数学模型由三相ABC静止坐标系转换到d-q旋转坐标系下。所以永磁同步电机在d-q轴旋转坐标系下的数学模型为[13]：

式中：ud，uq分别为d，q轴电压;id，iq分别为d，q轴电流;Rs为定子相电阻;Ld，Lq分别为d，q轴电感;ωr为电气角速度;ψf为转子磁链;p是微分算子。

选取转子结构为凸装式的永磁同步电机作为实验对象，它的特点是d，q轴同步电抗近似相等，即Ld=Lq=L。

对式(11)中的微分算子p进行离散化处理：

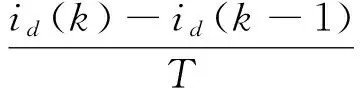
则：

于是可以得到永磁同步电机的自回归模型：

此处仅考虑d轴的电流电压情况，即：

所以永磁同步电机的自回归模型:

y(k)=φT(k)θ(k)

其中：

3 仿真实验

矢量控制是将定子侧三相电流正交分解为磁链方向和磁链正交方向两个电流分量，可以通过分别独立控制两个分量改变电流矢量的幅值和方向来调节转速，大大提高了电机的调速性能。

在Simulink中搭建永磁同步电机矢量控制模型，实时获得数据通过遗忘因子多新息随机梯度辨识模块进行参数辨识，如图1所示。

该模型是基于磁场定向控制，采用SVPWM矢量控制方法[14-15]，id=0和电流环与速度环双闭环控制策略。id=0控制方法是将永磁同步电机的d轴电流控制为零，当id=0时，电机的电磁转矩只与iq相关，可以只通过控制q轴电流大小控制电机运行，同时也进一步简化了永磁同步电机的数学模型。给定转速ω=2 000 r/min，采样时间T=0.001 s，将采集到的数据经过低通滤波器处理，以减少噪声对实验的干扰，低通滤波器截止频率设置为80 rad/s通过M文件编写在线辨识模块进行在线辨识。电机模型参数如下：

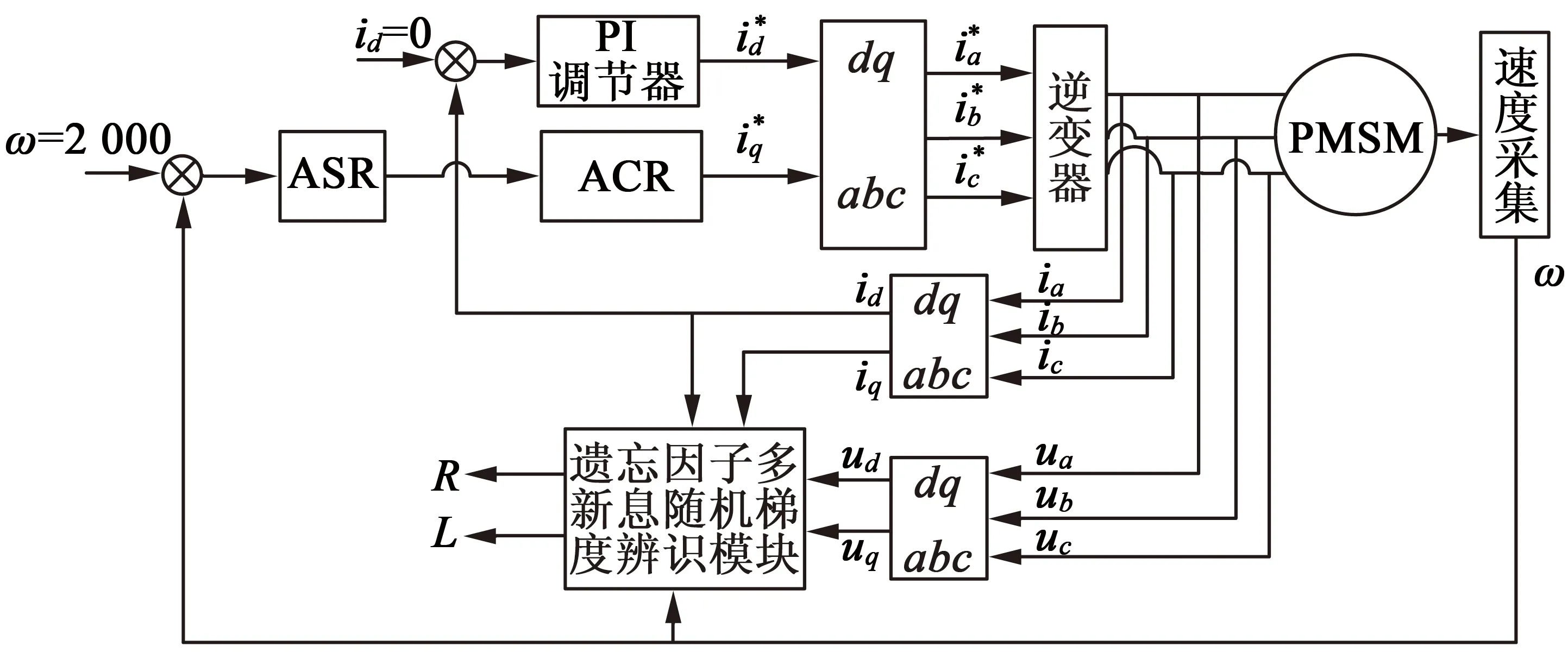
图1 矢量控制系统框图

表1 电机模型参数

图2表示的是电机起动的过程，达到设定的转速后，稳定在2 000 r/min，该矢量控制模型有很好的控制效果，同时也可以通过修改设定值进行调速。

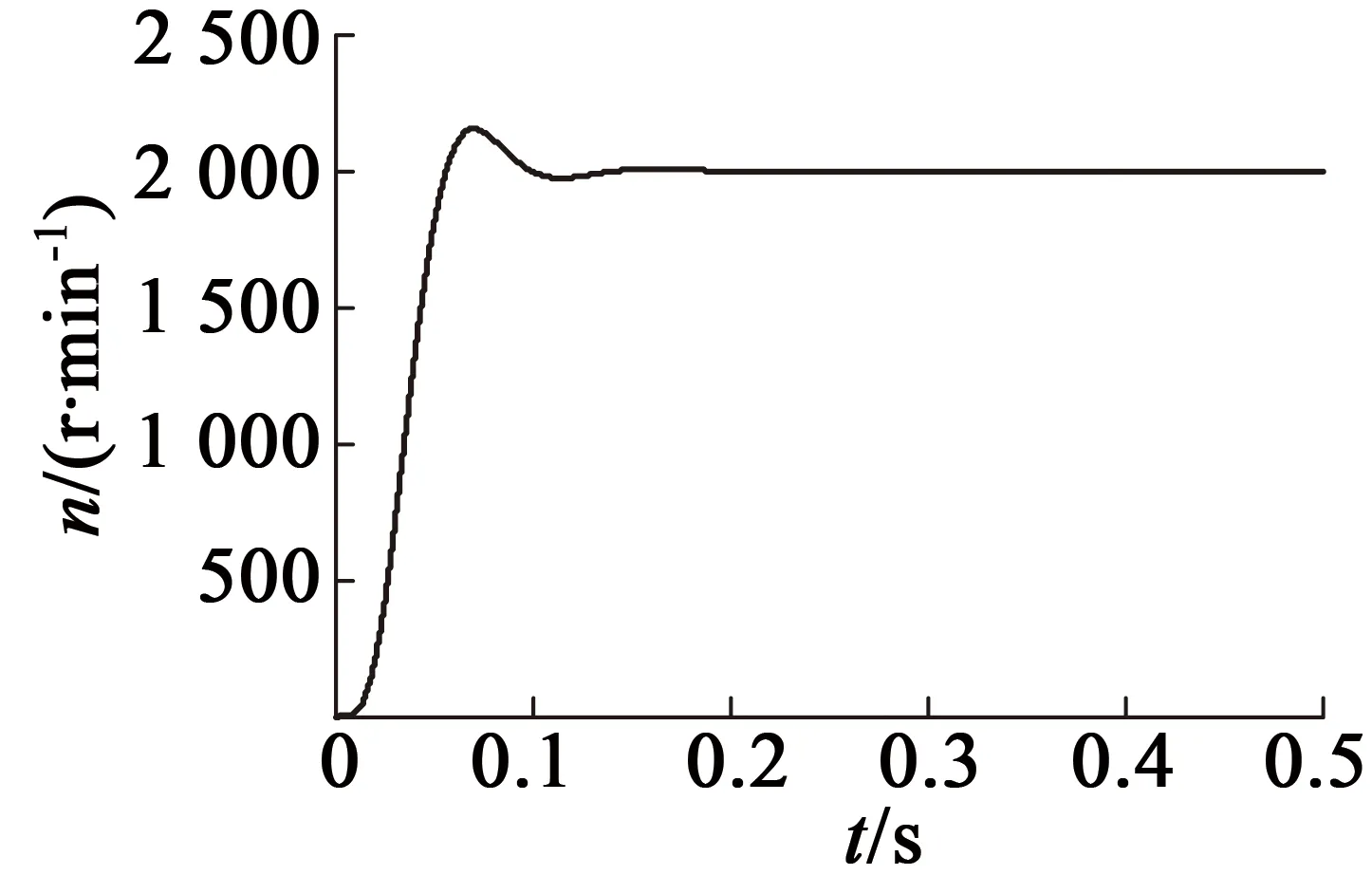
图2 速度响应(n=2 000 r/min)

参数辨识步骤：

1)采集电机中电流id，iq电压Ud，电气角速度ωr，采样周期T等数，并进行滤波处理：

2)根据式(12)、式(13)的值构造y(k),φ(k)；

3)根据式(6)、式(7)构造Φ(p,t),Y(p,t)；

4)根据式(5)计算E(p,t)，根据式(10)计算r(t)；

6)在线采集新数据，t=t+1，返回步骤2)。

3.1固定参数辨识

图3为遗忘因子随机梯度算法、遗忘因子多新息随机梯度算法、递推最小二乘算法(RLS)估计误差δ的收敛曲线。可以看出，遗忘因子多新息随机梯度算法比随机梯度算法在收敛速度和收敛精度上优势明显，并且当数据长度p=8时，收敛速度已经可以与递推最小二乘算法相当，收敛精度稍优于递推最小二乘算法。

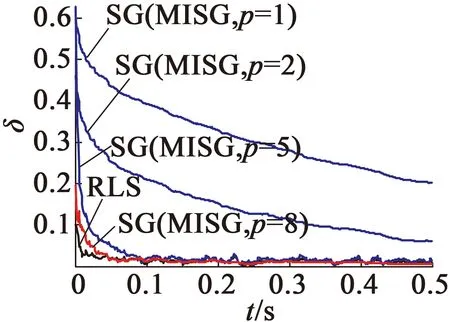
图3 SG，MISG和RLS算法的估计误差δ

图4、图5分别为用遗忘因子多新息随机梯度算法对电阻和电感在固定参数情况下在线辨识的结果。可以看出，固定参数情况下，电阻收敛快速，精度理想，与实际值基本吻合。电感的收敛速度和精度理想。

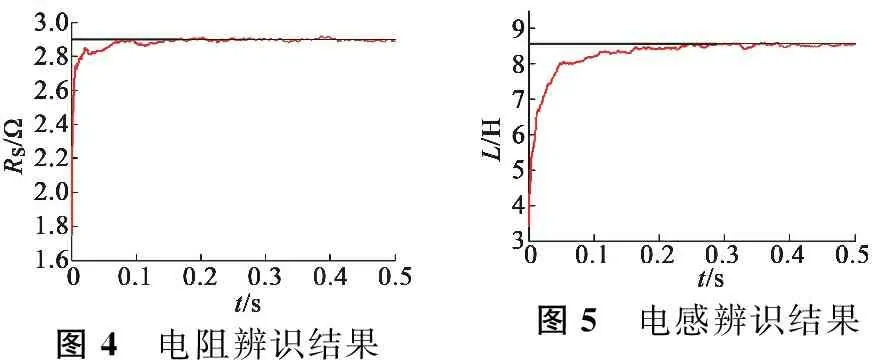
图4 电阻辨识结果图5 电感辨识结果

3.2变参数辨识

电机的运行情况十分复杂，容易受到环境的影响。表现比较明显的是电机的电阻和电感在温度变化时会受到影响。假定实验周围环境是随时间均匀变化的，将电阻、电感设定为随时间均匀增加，电阻的变化范围是2.875～3 Ω，电感的变化范围是0.008 5～0.008 9 H。通过采集到的数据进行参数辨识，得到电阻、电感的辨识效果如图6、图7所示。

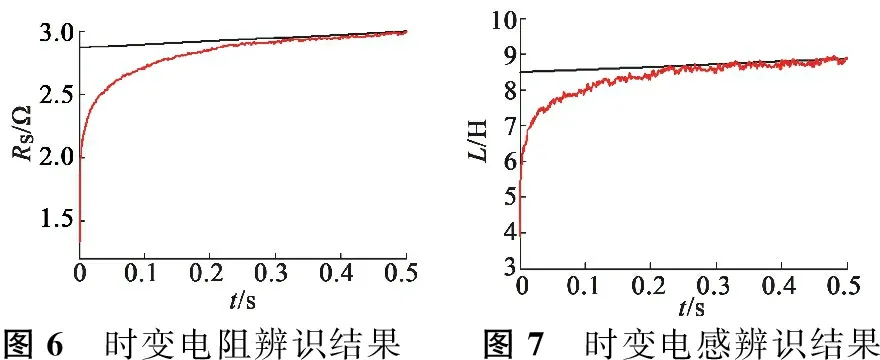
图6 时变电阻辨识结果图7 时变电感辨识结果

图6、图7分别是电阻和电感在随时间均匀增加情况下的辨识过程。可以看出辨识过程开始阶段，误差较大，随着新数据的更新，误差迅速减小，短时间内达到跟踪电阻和电感的变化，表明遗忘因子多新息随机梯度算法有很好的收敛速度和收敛精度。

4 结 语

本文介绍了基于遗忘因子多新息随机梯度算法的永磁同步电机参数辨识。将永磁同步电机数学模型转换为自回归模型，通过采集需要的数据，用上述算法精确辨识出定子电阻和定子电感。并且当电阻电感随温度等条件发生变化时，辨识结果能够精确跟踪电阻电感的变化趋势。综合以上结论，经过遗忘因子多新息随机梯度算法辨识得到的结果能够精确收敛到真实值，较随机梯度算法有较大优势，在精度上基本可以和递推最小二乘算法相媲美。

[1] 殷战稳,司纪凯.永磁直线同步电机应用现状综述[J].微电机,2012,45(1):76-80.

[2] 李高林,罗德荣,叶盛,等.基于电动车的永磁同步电机的弱磁控制[J].电力电子技术,2010,44(6):88-89.

[3] CAO Rongmin,ZHOU Huixing Z,HOU Zhongsheng,et al.Low-speed performance research for permanent magnet synchronous linear motor based on nonparametric model-learning adaptive control[C]//2011 International Conference on Electrical Machines and Systems (ICEMS).IEEE,2011:1-5.

[4] 邱鑫,黄文新,杨建飞,等.一种基于转矩角的永磁同步电机直接转矩控制[J].电工技术学报,2013,28(3):56-62.

[5] YOUSEFI I,GHANBARI M.Parameter estimation of permanent magnet synchronous motor using orthogonal projection and recursive least squares combinatorial algorithm[J].Mathematical Problems in Engineering,2015(1):1-7.

[6] 王庆龙,张兴,张崇巍.永磁同步电机矢量控制双滑模模型参考自适应系统转速辨识[J].中国电机工程学报,2014,34(6):897-902.

[7] 曹杨.永磁同步电机参数辨识研究[D].济南：山东大学,2014.

[8] DING F,CHEN H,LI M.Multi-innovation least squares identification methods based on the auxiliary model for MISO systems[J].Applied Mathematics and Computation,2007,187(2):658-668.

[9] 丁锋,萧德云,丁韬.多新息随机梯度辨识方法[J]. 控制理论与应用,2004,20(6):870-874.

[10] DING F,CHEN T.Performance analysis of multi-innovation gradient type identification methods[J].Automatica,2007,43(1): 1-14.

[11] 刘英玉,申东日,陈义俊,等.基于前向神经网络的多新息随机梯度辨识算法[J].哈尔滨商业大学学报:自然科学版,2006,22(2):83-86.

[12] 于丽,丁锋,张佳波.多新息随机梯度辨识方法的收敛性研究[J].科学技术与工程,2007,7(21):5475-5478.

[13] 王伟华,肖曦,丁有爽.永磁同步电机改进电流预测控制[J].电工技术学报,2013,28(3):50-55.

[14] HEMALATHA G,CHINNAIYAN V K.Performance analysis of permanent magnet synchronous motor using SVPWM technique[C]//2014 International Conference on Green Computing Communication and Electrical Engineering (ICGCCEE).IEEE,2014:1-5.

[15] GU M,OGASAWARA S,TAKEMOTO M.Sensorless IPMSM position estimation based on multi SVPWM with elimination of inverter nonlinear effects[J].IEEJ Transactions on Electrical and Electronic Engineering,2014,9(2):219-227.

ParameterIdentificationforPMSMBasedonForgettingFactorMulti-InnovationStochasticGradientIdentificationAlgorithm

ZHANGJian-yu,WUDing-hui

(Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Jiangnan University, Wuxi 214122,China)

In view of the problem that the results of traditional identification algorithm are not accurate and parameters variation of motor, a new algorithm based on the forgetting factor multi-innovation stochastic gradient identification algorithm is proposed. Combined with permanent magnet synchronous motor (PMSM) system voltage equation, a discrete identification model is constructed. By using vector control method, the input and output data of the identification model are obtained to identify the rotor resistance and inductance. The simulation results show that this identification algorithm can obtain the accurate parameters of the PMSM model.

permanent magnet synchronous motor (PMSM); SVPWM vector control; forgetting factor; multi-innovation stochastic gradient algorithm; parameter identification

2015-09-14

国家高技术研究发展计划项目(2013AA040405)；江苏省食品先进制造装备技术重点实验室项目(FM-201408)；江苏省“六大人才高峰”项目(WLW-008)

TM351;TM341

：A

：1004-7018(2016)11-0066-04

张建宇(1992-)，男,硕士研究生。