有限元法结合压痕法估算BNKT薄膜的压电应力常数*
2016-08-26郑学军
王 巍, 苏 亮, 郑学军,3*
(1.上海理工大学 环境与建筑学院,上海 200093;2.湘潭大学 机械工程学院,湖南 湘潭 411105;3.上海理工大学 材料科学与工程学院,上海 200093)
有限元法结合压痕法估算BNKT薄膜的压电应力常数*
王巍1,苏亮2,郑学军2,3*
(1.上海理工大学 环境与建筑学院,上海 200093;2.湘潭大学 机械工程学院,湖南 湘潭 411105;3.上海理工大学 材料科学与工程学院,上海 200093)
考虑基底效应的影响,将压电应变系数与压电应力常数的关系式作为补充方程,通过有限元法结合纳米压痕法估算了横观各向同性0.85Na0.5Bi0.5TiO3-0.15K0.5Bi0.5TiO3(BNKT)薄膜的压电应力常数.在正向分析中,通过无量纲分析和有限元模拟,得到最大压痕荷载、加载曲线指数与BNKT薄膜压电应力常数之间的无量纲方程.在反向分析中,利用纳米压痕实验得到沉积在硅基底上BNKT薄膜的压痕曲线,将实验数曲线中的最大压痕荷载和加载曲线指数代入正向分析建立的无量纲方程,联立补充方程进行求解,得到多组不同误差下的解,取误差最小时相应的解e15= 0.28 C/m2, e31= 7.72 C/m2, e33=18.26 C/m2为BNKT薄膜的压电应力常数.
纳米压痕;压电应力常数;有限元法;横观各向同性压电薄膜
压电薄膜是一种用人工方法合成的,通常以沉积在基底上的形式存在,其厚度在纳米至微米量级.压电薄膜材料作为一种功能材料,具有优异的力电耦合性能,广泛应用于微电机系统中的制动器、传感器和位移器等电子元器件,还应用于微机装配、自动控制、精密仪器等领域[1,2].由于压电薄膜的广泛应用,正确表征压电薄膜的力电性能显得十分重要.压痕技术是表征材料力学性能的有效手段,传统的压痕技术通过压痕测试过程中所得到的压痕载荷、投影接触面积和压痕深度等一系列的实验数据来评价材料的力学性能[3].传统的压痕测试方法将薄膜看成各向同性材料,这样简化不能表征纳米薄膜的横观各向同性材料.Zheng等利用正反向分析,采用Berkovich形状的压头进行纳米压痕实验结合有限元的方法,表征了纳米薄膜材料的弹性力学参数[4].
本文考虑基底效应的影响,将压电应变系数与压电应力常数的关系式作为补充方程,通过无量纲分析和有限元模拟研究了压电应力常数对压痕响应过程中最大压痕载荷和加载曲线指数的影响,得到最大压痕载荷、加载曲线指数与压电应力常数之间的无量纲方程.利用纳米压痕实验得到沉积在硅基底上BNKT薄膜的压痕曲线,将实验数曲线中的最大压痕荷载和加载曲线指数代入无量纲方程,联立补充方程,估算横观各向同性BNKT薄膜压电应力常数.
1 压痕模型
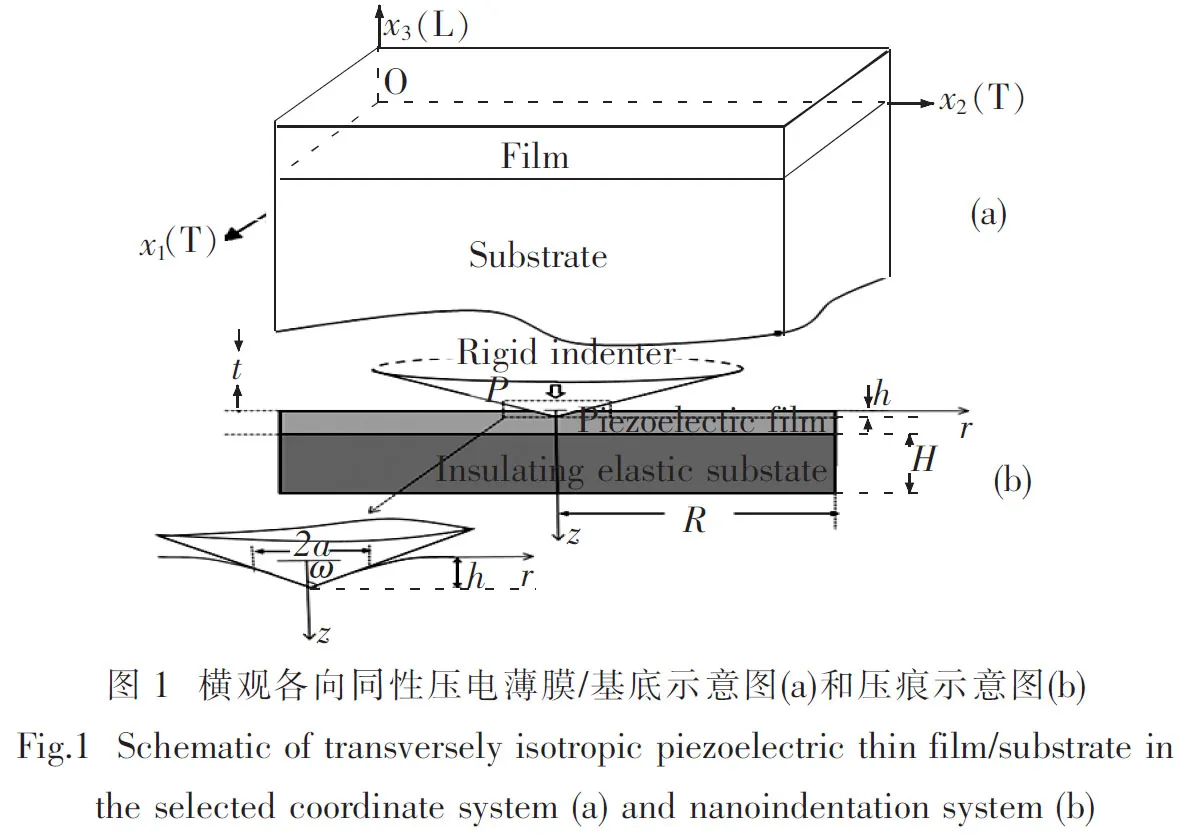
BNKT薄膜属于横观各向同性材料,它常常以沉积在基底表面的形式存在,如图1所示.x1-x2为横观各向同性面,x3为垂直于横观各向同性面的纵向对称轴,下标1和2表示横向同性方向(T),3表示纵向对称轴方向(L).图1(b)为膜/基底体系的压痕示意图,其中P和h分别表示压痕载荷和压痕深度,t、H和R分别是薄膜厚度以及基底的厚度和半径.纳米压痕实验中,Berkovich压头是应用较为广泛的一种,为了方便地处理压头的几何模型,可由半角为70.3°的刚性圆锥型压头来代替[4].另外,假设薄膜与基底之间的结合面为理想结合面,且压头与薄膜之间的摩擦力可以忽略不计[5].
对于横观各向同性压电材料,其本构方程为[4]

(1)
式中,sij为弹性顺度系数,dkj为压电应变系数,ξkl为介电系数,Dk为电位移,El为电场强度.其中压电应变系数可以由压电应力常数ekj表示为dkj=ekisji,弹性顺度系数矩阵可以描述为[4]

(2)
式中,ET、EL分别表示横向和纵向弹性模量,GT、GL分别表示横向和纵向剪切模量,νTL、νLT和νT是材料的泊松比,以上七个弹性力学参数之间并非独立的,其中,νTL/ET=νLT/EL,且GT可由ET和νT表示[4].
由本构方程(1)和(2)知,横观各向同性材料的特征参数包括5个弹性模量、3个压电应力常数和2个介电系数[4].本文求解的是材料的压电应力常数,而材料的特征参数有10个独立参数,因此需要对材料模型进行简化,将未知的材料特征参数的个数减少到只剩3个压电应力常数.对于横观各向同性材料,泊松比νTL和νLT之和被认为是横向面内泊松比νT的两倍[6].一般近似取νT为0.3[4].当材料的弹性模量和介电系数已知时,则横观各向同性材料未知的特征参数就只剩3个压电应力常数.
2 正向分析
2.1压痕响应的无量纲分析

F=Fm(h/hm)x.
(3)
纳米薄膜/基底体系的压痕实验表明,最大压痕载荷Fm和加载曲线指数x是与材料参数和实验数据相关的函数[4,9].当压电纳米带材料的弹性模量和介电系数作为已知量时,影响压痕响应的独立未知材料参数有纳米薄膜的压电应力常数(e15,e31,e33)、基底的弹性模量Es、纳米薄膜的厚度t以及最大压痕深度hm.于是,Fm和x可表达为
Fm=α0(e15,e31,e33,t,Es,hm),
(4)
x=β0(e15,e31,e33,t,Es,hm),
(5)
其中,Es、t和hm通过纳米压痕实验获得.为了模拟数值加载曲线,将这些参数当作已知对待,而最大压痕载荷和加载曲线指数可以通过压痕实验加载曲线提取.根据π定理[4],对(4)和(5)式进行无量纲分析可得

(6)
x=β(e15/e33,e31/e33).
(7)
根据(6)和(7)式,只能解出e15/e33和e31/e33两个参数.为了确定每个压电应力常数,需要一个补充方程.
压电应变系数d33是表征压电材料压电性能的参数,其与压电应力常数存在如下关系[10]
d33=2e31s13+e33s33,

(8)
其中,弹性顺度系数s13和s33可由(2)式求得,d33值通过测试可得.将方程(8)作为求解压电应力常数的补充方程.
2.2有限元模拟及无量纲方程拟合
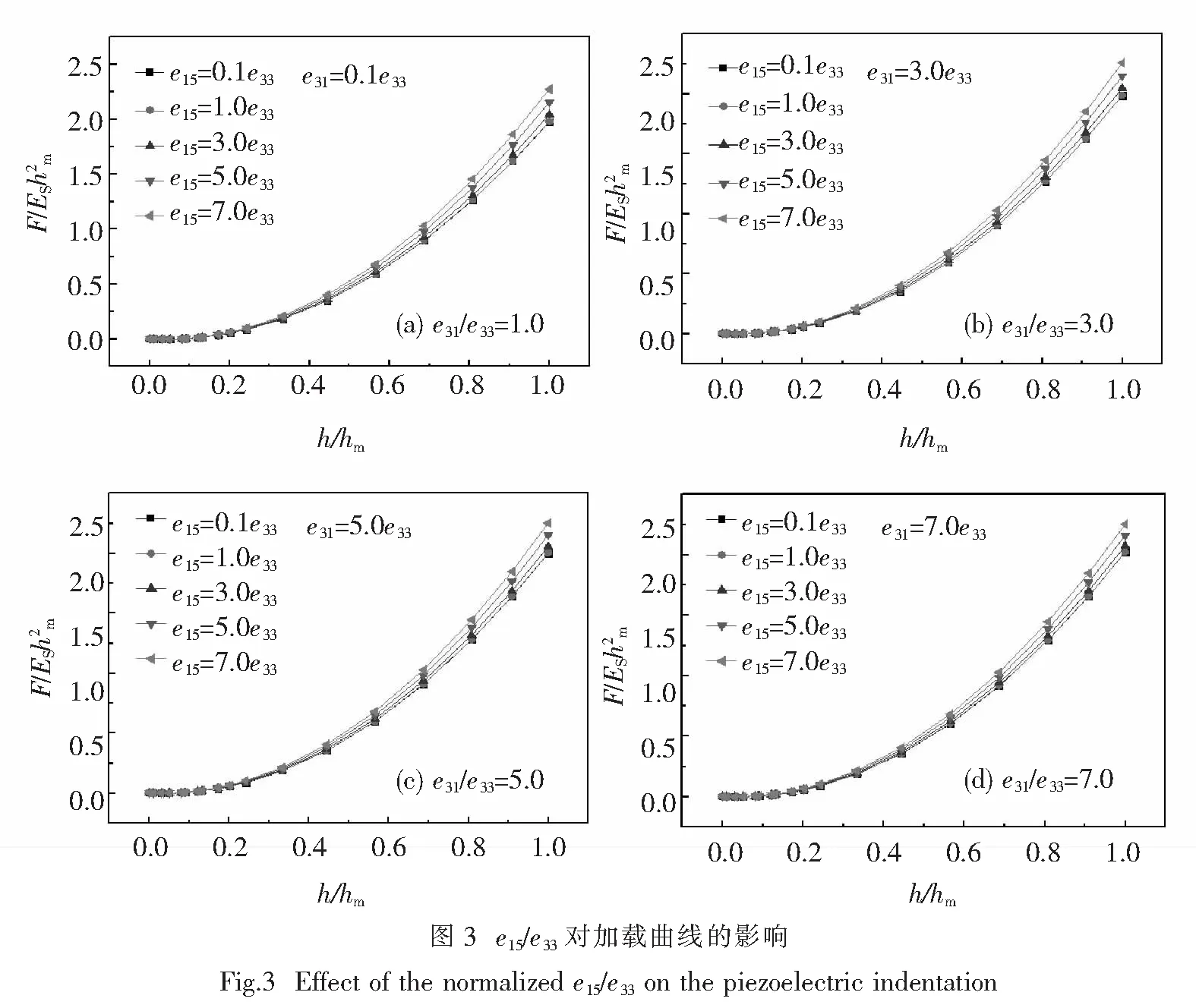
利用有限元软件ABAQUS建立二维轴对称膜/基体系的模型,网格划分如图2所示.模型中BNKT薄膜的参数t=350 nm,ET=113.5 GPa,EL=169.5 GPa,GL=60 GPa,介电系数κ11=2.04×10-10F/m,κ33=10.9×10-10F/m[9,11,12],最大压痕深度hm为40 nm.考虑到涵盖较大的材料范围,选择较宽的材料范围0 (9) x=β(A,B)=L1+L2A+L3A2+(L4+L5A+L6A2)B+(L7+L8A+L9A2)B2, (10) 表1 方程(9)和(10)中的拟合系数Tab.1 The fitting coefficients of Eqs. (9) and (10) 其中,A=e15/e33和B=e31/e33,方程(9)和(10)中拟合系数Ki和Lj(i=1,2,…,9,j=1,2,…,9)的具体数值列于表1. 3.1估算BNKT压电薄膜的压电应力常数 表2 BNKT薄膜反向分析的多组解Tab.2 The multiple solutions to reverse analysis for BNKT film 3.2验证解的合理性 为了验证解的合理性,将S1、S2和S3对应的模拟数值加载曲线与实验加载曲线对比,如图6所示.误差最小(S3)对应的数值加载曲线最接近实验加载曲线;将S3对应的压电应力常数与文献[11]中的压电应力常数e15=0.3 C/m2,e31=7.699 C/m2和e33=19.62 C/m2相比,相对误差为0.2%~6.9%.因此,本文估算的结果是合理的. 在考虑基底效应的情况下,将压电应变系数与压电应力常数关系式作为补充方程,提出有限元模拟结合纳米压痕实验来确定压电薄膜压电应力常数的方法.正向分析,通过无量纲分析和有限元模拟得到了压痕响应过程中最大压痕载荷、加载曲线指数和压电应力常数之间的无量纲方程;反向分析,利用纳米压痕测试,得到BNKT压电薄膜材料的最大压痕载荷和加载曲线指数,代入无量纲方程,结合补充方程估算BNKT压电薄膜的压电应力常数.将所求得的结果反代回有限元软件ABAQUS得到数值加载曲线与实验加载曲线,对比发现符合较好,并与文献中报道的结果比较接近,这说明通过结合有限元模拟和纳米压痕实验可以有效地确定横观各向同性压电薄膜材料的压电应力常数. [1]HE J H, TE HO S, WU T B, et al. Electrical and photoelectrical performances of nano-photodiode based on ZnO nanowires[J]. Chemical Physics Letters, 2007, 435(1): 119-122. [2]ZHENG X J,CHEN Y Q,ZHANG T,et al. A photoconductive semiconductor switch based on an individual ZnS nanobelt [J]. Scripta Materialia, 2010, 62: 520-523. [3]BOCCIARELLI M, BOLZON G, MAIER G. Parameter identification in anisotropic elastoplasticity by indentation and imprint mapping [J]. Mechanics of Materials, 2005,37:855-868. [4]WANG J S, ZHENG X J, ZHENG H, et al. Identification of elastic parameters of transversely isotropic thin films by combining nanoindentation and FEM analysis[J]. Computational Materials Science, 2010, 49(2): 378-385. [5]CHEN W M, CHENG Y T, LI M. Indentation of power law creep solids by self-similar indenters[J]. Materials Science and Engineering: A, 2010, 527(21): 5 613-5 618. [6]NAKAMURA T, GU Y. Identification of elastic-plastic anisotropic parameters using instrumented indentation and inverse analysis[J]. Mechanics of Materials, 2007, 39(4): 340-356. [7]ZHAO M, CHEN X, XIANG Y, et al. Measuring elastoplastic properties of thin films on an elastic substrate using sharp indentation[J]. Acta Materialia, 2007, 55(18): 6 260-6 274. [8]WANG J S, ZHENG X J, ZHENG H, et al. Evaluation of the substrate effect on indentation behavior of film/substrate system[J]. Applied Surface Science, 2010, 256(20): 5 998-6 002. [9]ZHENG H, ZHENG X J, SONG S T, et al. Evaluation of the elastic modulus of thin film considering the substrate effect and geometry effect of indenter tip[J]. Computational Materials Science, 2011, 50(10):3 026-3 031. [10]DAMJANOVIC D. Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics[J]. Reports on Progress in Physics, 1998, 61(9): 1 267. [11]ISUPOV V A. Ferroelectric Na0.5Bi0.5TiO3and K0.5Bi0.5TiO3perovskites and their solid solutions[J]. Ferroelectrics, 2005, 315(1): 123-147. [12]ZHAN K, ZHENG X J, PENG J F, et al. Effects of potassium content on the electrical and mechanical properties of (Na1-xKx)0.5Bi0.5TiO3thin films[J]. Ceramics International, 2015, 41(3): 3 474-3 480. [13]SONG S T, ZHENG X J, ZHENG H, et al. Evaluation of engineering/piezoelectric constants of piezoelectric thin film by combining nanoindentation test with FEM[J]. Computational Materials Science, 2012, 63: 134-144. [14]ZHENG H, ZHENG X J, WANG J S, et al. Evaluation the effect of aspect ratio for Young’s modulus of nanobelt using finite element method[J]. Materials & Design, 2011,32(3):1 407-1 413. 责任编辑:罗联 Evaluation of the Piezoelectric Stress Constants of BNKT Film by Combining Nanoindentation Test with Finite Element Method WANGWei1,SULiang2,ZHENGXue-jun2,3* (1.School of Environment & Architecture, University of Shanghai for Science & Technology, Shanghai 200093;2. School of Mechanical Engineering, Xiangtan University, Xiangtan 411105;3.School of Materials Science & Engineering, University of Shanghai for Science & Technology, Shanghai 200093 China) With assistance of the substrate effect, the piezoelectric constitution is used to establish the supplemental equation, in which the piezoelectric strain constants are related with the piezoelectric stress constants, so that the piezoelectric stress constants of transversely isotropic 0.85Na0.5Bi0.5TiO3-0.15K0.5Bi0.5TiO3(BNKT) thin film can be evaluated by combining nanoindentation test with finite element method (FEM) simulation. In the forward analysis, the nanoindentation responses are simulated by using FEM to extract the numerical maximum indentation loads and the loading curve exponents, and they are used to establish two dimensionless equations related with the piezoelectric stress constants of BNKT thin film /substrate system. In the reverse analysis, the experimental indentation curves performed on BNKT thin film in nanoindentation test are fitted as the power function to obtain the maximum indentation loads and the loading curve exponents, and they are substituted into the dimensionless equations. The multiple solutions are obtained by using the simultaneity of dimensionless and supplemental equations, and the combination of piezoelectric stress constants is taken as the ultimate solution with the smallest total error. The results show that the piezoelectric stress constants of the BNKT thin film are determined as e15=0.28 C/m2, e31=7.72 C/m2,and e33=18.26 C/m2. nanoindentation; piezoelectric stress constants; finite element method; transversely isotropic piezoelectric thin film 2015-10-07 国家自然科学基金项目 (51272158);教育部创新团队滚动资助项目(IRT-14R48);教育部“长江学者计划”特聘教授项目([2009]17) 郑学军(1963-),男,湖南 株洲人,教授,博士生导师. E-mail:zhengxuejun@xtu.edu.cn TB303 A 1000-5900(2016)01-0015-06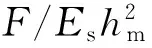

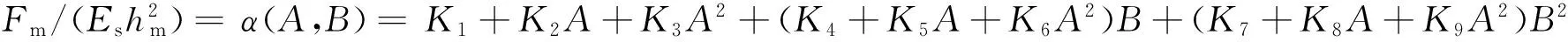

3 反向分析


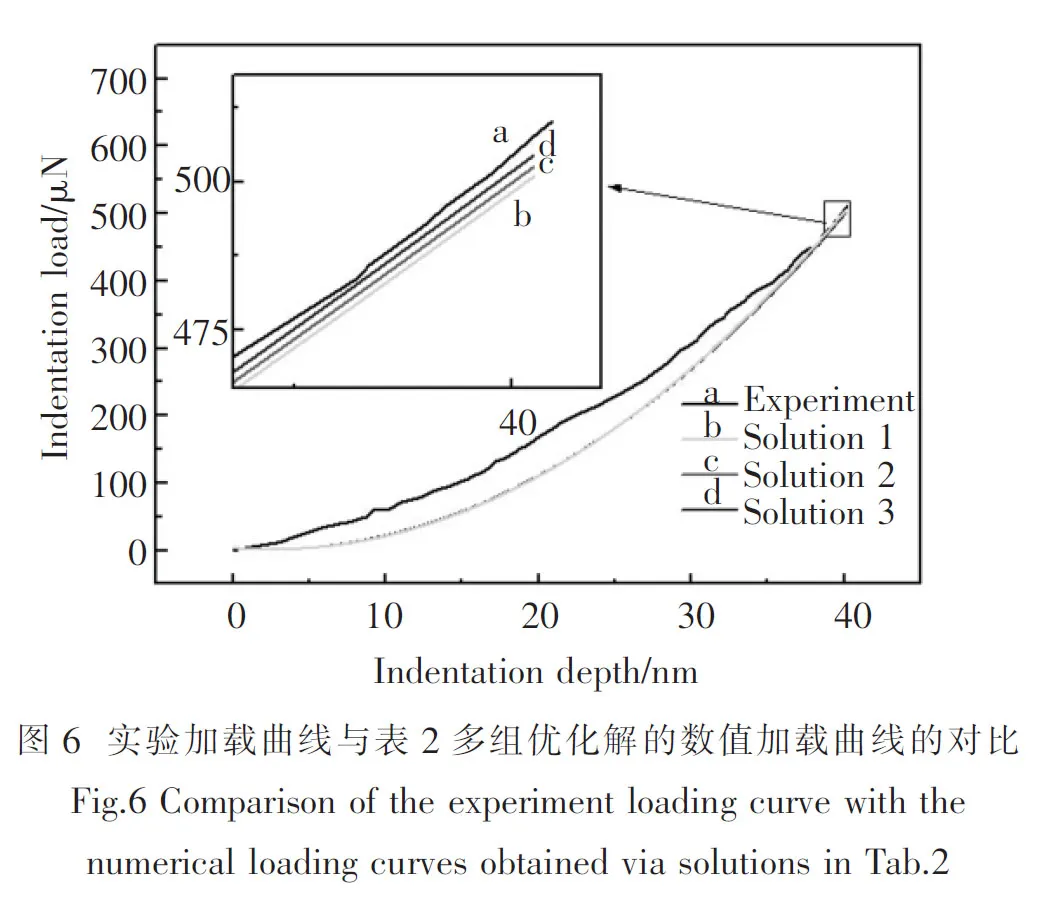
4 结 论
