三自由飞行模拟器的动力学分析与仿真

韩红伟，党淑雯，何法江HAN Hong-wei，　DANG Shu-wen，　HE Fa-jiang（.上海工程技术大学 机械工程学院，上海 060；.上海工程技术大学 航空运输学院，上海 060）

三自由飞行模拟器的动力学分析与仿真

韩红伟1，党淑雯2，何法江2
HAN Hong-wei1，DANG Shu-wen2，HE Fa-jiang2
（1.上海工程技术大学 机械工程学院，上海 201620；2.上海工程技术大学 航空运输学院，上海 201620）

建立精确的动力学模型是飞行模拟器研制开发和提高模拟性能的重中之重。以3-RPS并联机构的三自由度飞行模拟器运动平台为研究对象，考虑到机构质量、荷载、转动惯量和惯性力的影响，建立了基于Kane方法的改进型多刚体动力学方程。采用ADAMS和UG联合仿真，在运动平台中心分别施加随时间变化的力和额定荷载，得出升降、俯仰、横滚飞行姿态下，各个驱动系统的受力以及相应旋转副的转矩。仿真结果表明：飞行模拟器运动平台的承载能力足够，满足模拟运动的技术指标要求；各个驱动缸受力和所受转矩均衡，从而验证了动力学模型建立的正确性和运动平台结构设计的合理性。该研究方法适用于其他并联机构和模拟器的动力学研究，具有一定的推广意义。

三自由度飞行模拟器；动力学模型；承载能力；ADAMS

0　引言

飞行模拟器是模拟飞行员飞行训练的机构，因其安全、经济、有效等特点近年来得到了广泛关注。选用三自由度并联机构作为飞行模拟器的运动平台，该类运动平台多用于地面训练所用的飞行模拟器。

动力学模型是对机构进行动力学分析和研究的基础，并联机构作为飞行模拟器的运动平台，动力学模型关系到飞行姿态动力控制的精度、飞行性能的分析以及优化，因此建立准确的动力学模型至关重要。求解并联机构动力学方程的方法有牛顿欧拉法（Newton-Euler）、拉格朗日方程法（Lagrange）、凯恩方程法（Kane）、虚功原理等。牛顿欧拉法和拉格朗日法主要针对单刚体系统或者刚体较少的系统。凯恩法和虚功原理适用于多刚体系统。文献［1～3］分别考虑支链绕自身轴线的转动、静态摩擦、重力及关节处的各种摩擦力给并联机构运动平台动力学模型带来的误差，建立了精确的动力学模型。文献［4，5］先后对6-DOF并联机器人的Newton-Euler动力学模型进行简化并针对Lagrange动力学模型做出改进。文献［6］选取动平台中心点的速度和角速度分量为广义速率，以Kane方程为基础推导出并联机器人的动力学方程。文献［7］考虑到运动副之间的间隙和摩擦，建立了精确的动力学方程并对其进行了分析。

由于Kane方法只需要求导，对矢量的点积进行计算，计算过程中不出现内力，计算速度较快，文中以3-RPS运动平台为基础的飞行模拟器整体为多刚体系统，故选用Kane方法建立精确的动力学模型时，综合考虑了动平台连同载重的质量、驱动支链的质量、惯性力以及其绕自身轴线的转动所带来的影响。基于该动力学模型用ADAMS和UG联合仿真，在动平台中心处添加随时间变化的力，校核飞行模拟器在各种飞行姿态下的承载能力，在此基础上测得额定荷载下，模拟飞行姿态驱动支链的受力和所受转矩情况，从而验证模型结构的合理性。

1　动力学方程的建立

三自由度并联机构是少自由度并联机构的典型，3-RPS机构作为三自由度并联机构中的一种，近年来也被广泛关注。其结构简图如图1所示，由一个动平台、一个定平台、三个驱动支链组成，其中驱动支链系统为电动缸。由于三个驱动支链系统结构相同，所以只需对一个支链进行分析，即可得到整个系统的动力学方程。

1.1坐标系的建立

为了方便描述3-RPS运动平台的特点，确定动平台和驱动支链之间的位置、速度、加速度关系，建立如图1所示的坐标系，包括一个动坐标系和一个静坐标系坐标系的建立利于动平台相对静平台的位置姿态的确立。通过三个驱动支链实现飞行姿态的改变，用指定的运动向量q表示，其中两坐标系的位置关系可用两坐标原点的位置矢量t表示。其中表示动平台在静坐标系下的欧拉角。

根据欧拉角旋转的先后顺序和不同坐标轴间的组合，可以形成多达24种不同的欧拉角组合［8］。本文采用XYZ（或称1-2-3）欧拉角来对运动平台的姿态进行描述。

XYZ欧拉角涉及到坐标系的三次连续旋转，如图2所示。

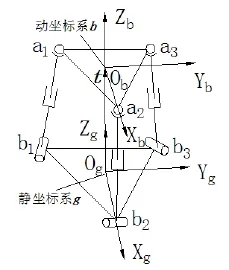
图1　3-RPS飞行模拟器运动平台结构简图

图2　坐标旋转变换

动平台的相对静坐标系在空间位姿可依据以上六个参数唯一确定。对于动平台铰接点相对动坐标系的坐标可以表示为用坐标矩阵表示，静平台铰接点相对于静坐标系的坐标可以表示为用坐标矩阵表示。

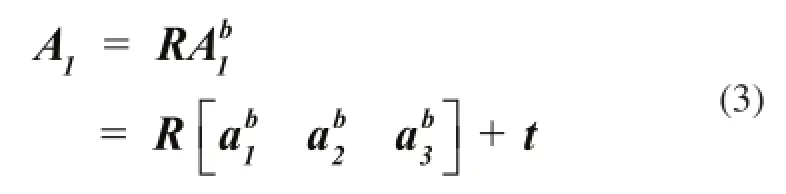
电动缸由定缸和动缸两个刚体组成，其中上部分为动缸、下部分为定缸，矢量图如图3所示。

图3　支链矢量图

1.2运动学分析

根据空间矢量关系，三个电动驱动缸长度矢量li（i=1，2，3）可表示为：

从而电动缸的长度可表示为：

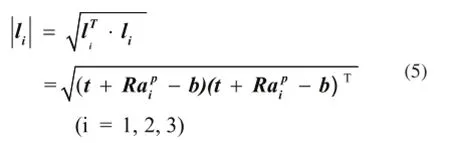
若设各个电动缸的初始长度为l0，则电动缸的伸长量为：

动平台在静坐标系中的广义速度表示为：

式中ω为动平台相对静坐标系的角速度矢量。根据文献［9］可知，角速度矢量可分解为绕x，y'，z''各坐标轴的角速度的矢量和为：

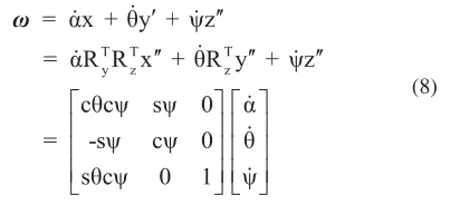
对式（5）两边同时求导整理得电动驱动缸上铰点的速度和加速度分别为：

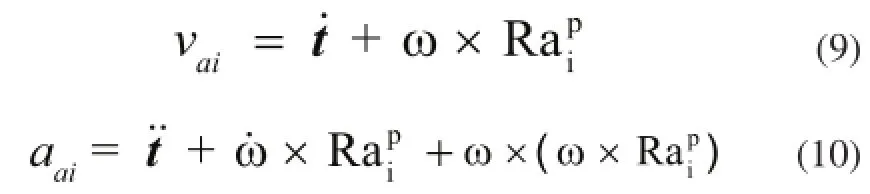
三个电动驱动缸的伸长速度为上铰点速度在伸长方向的投影表示为：

式中，Ln为三个电动驱动缸单位方向矢量组成的矩阵，Ap上铰点在静坐标系中的坐标矩阵，Jlq为动平台广义速度到电动缸伸长速度的雅可比矩阵。

由角速度的性质可知电动驱动缸的角速度和角加速度分别为：

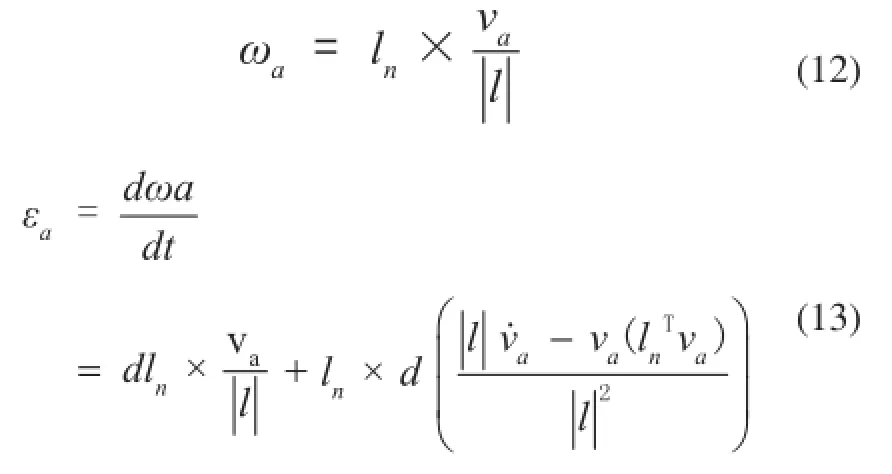
电动缸动缸在运动中既有平动又有转动，其质心ac到上铰点的距离为ra，而电动缸定缸在运动中只有转动，其质心bc到下铰点的距离为rb。其质心的速度和加速度表达式都可以通过va分别示：

1.3动力学方程的建立

1.3.1动平台及负载质量影响下的动力学模型［10］

由牛顿第二定律，建立动平台在平动方向的力平衡方程：

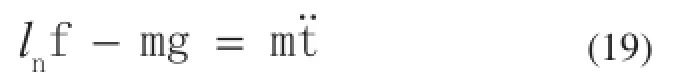
式中，f为电动缸产生的主动力矢量，m为上平台及负载的总质量，g为重力加速度向量

动平台在旋转方向的运动学方程表示为：

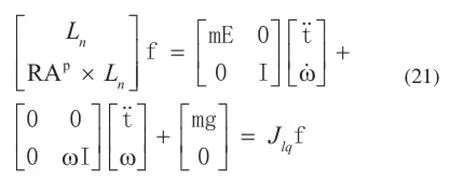
式中E为3×3的单位矩阵。

1.3.2电动缸质量及转动惯量影响下的动力学模型

设动缸质量为ma，定缸质量为mb，Ia为动缸在ac点绕垂直于电动缸轴线的惯量，Ib为动缸绕下铰点转动的惯量，则动缸相对于自身质心ac的平移惯性力记为fac则：

由式（16）电动缸平移运动时，动缸的平移惯性力在上铰点处的投影表示为：

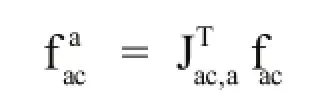
利用欧拉方程，并通过投影变换得到电动缸的定缸和动缸绕下铰点转动的惯性力的表达式。

把式（12）写成矩阵形式为：

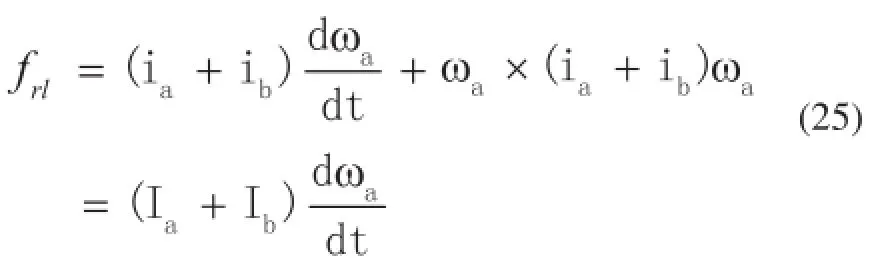
式中，ia，ib分别为电动缸动缸、定缸的质量矩阵。

将电动缸在下铰点转动惯性力向上铰点空间投影，可得到电动缸在上铰点转动的惯性力为：

将定缸和动缸的重力向上铰点投影得：

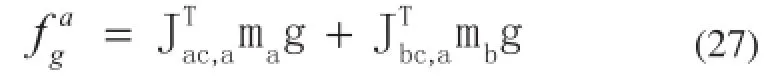
从而得该并联机构的精确的动力学方程 。

2　飞行模拟器的承载能力分析

参照模型飞行模拟器［11］，给出本文所设计的飞行模拟器技术参数，即：承载能力不小于3T且垂直瞬时加速度不小于0.5g。

由上述技术指标要求，驱动系统承受的静重W为3000kg，动平台的垂直瞬时加速度amax为0.5g，运动状态下，驱动系统的瞬时荷载F为45000N，单只电动缸的瞬时荷载f为15000N，即单只电动缸的额定荷载为15000N。宏观上，承载能力是指空间上的最大容量或力学上的最大限度。按照上述理解，飞行模拟器的最大承载能力可定义为飞行模拟器运动平台所能承受的最大外荷载［12］。

由文献［8］可得运动平台的力平衡方程：

式中，Gf为力映射矩阵；FG、FI分别为平台构件重力、惯性力；FE为外荷载；f为驱动力。

FE与运动平台构型、机构、驱动性能和机构运动状态有关，Gf由运动平台的机构构型和结构参数决定，反映了机构的本质。运动平台在某一确定姿态下，FG、FI与构件本身的结构和具体运动的运动状态有关，Gf不会改变。由于运动平台构件重力和惯性力相对其承载力所占比例较小，这里忽略不计，将式（30）可以改写为：

从上式可以看出f取得极值时，F的取值完全可以反映运动平台的承载能力。

2.1导入模型

本文采用UG环境下建立三维数据模型，然后以ADAMS/View识别较好的Parasolid格式导入，得到ADAMS/View的仿真模型，把各个零部件重新命名并赋予其质量。设定动、静平台的外接圆半径分别为r1、r2和电动缸的定缸、动缸的长度分别为l1、l2。

2.2添加约束

按照UG中建模的先后顺序，静平台固定不动和大地相连，在静平台上添加固定副，在电动缸的定缸和静平台之间添加转动副，在电动缸的定缸和动缸之间添加移动副，在动缸和动平台之间添加球副。考虑到各驱动支链绕固定转轴的转动和自身的转动，分别设置各支链在对应转轴处的转动惯量。所得到的虚拟样机如图4所示。

2.3承载能力分析

虚拟样机的四个结构尺寸分别为：r1=1154.7mm，r2=1443.4mm，定缸长度l1=750.096mm，动缸长度l2=803.3607mm。各个零部件的质量如下：静平台的质量为846.63kg，电动缸的定缸质量为14.67kg，动缸的质量为8.37kg，动平台的质量为548.34kg。这里规定飞行模拟器座舱安装方位为驱动支链2位于前端，1、3位于后端。在三个驱动支链的移动副上分别添加驱动，在其中的两个移动副添加传感器限制移动副，传感器的表达式为位移，限制移动副的行程为-220mm～220mm，仿真时间设置为1s，步长为30［13］。动平台的中心施加竖直向下的力为F=60000×time，分别模拟飞行模拟器在升降、俯仰、横滚三种姿态下，各个电动驱动缸在沿X、

Y、Z方向的受力情况，根据沿X、Y、Z轴线方向驱动支链达到最大额定荷载时刻，运动平台中心所对应的力来判断飞行模拟器的承载能力［14］。

2.3.1升降运动

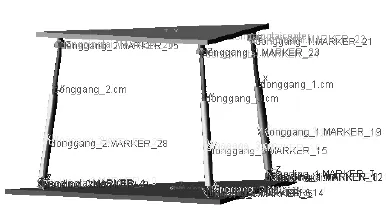
图4　虚拟样机

驱动支链1、2、3的在X、Y、Z方向的受力情况如图5所示。

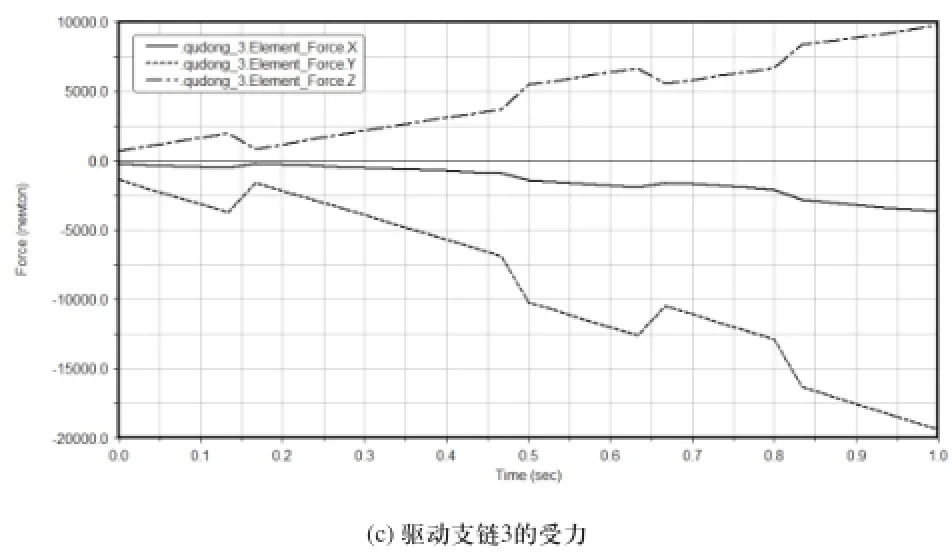
图5　驱动支链受力图

从图5升降运动驱动支链受力仿真结果可以看出，各驱动支链的在沿各个轴线方向受力曲线图中，沿Y轴方向受力最大，这里给出各驱动支链Y轴的受力数据分析，如表1所示。

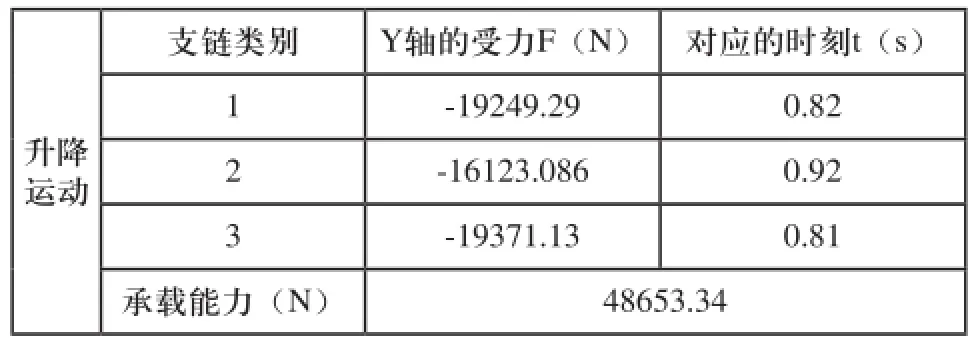
表1　升降运动下各支链受力情况

2.3.2俯仰运动

驱动支链1、2、3的在X、Y、Z方向的受力情况如图6所示。

图6　俯仰运动驱动支链受力

从图6俯仰运动驱动支链受力仿真结果可以看出，各驱动支链的在沿各个轴线方向受力曲线图中，沿Y轴方向受力最大，这里给出各驱动支链Y轴的受力数据分析，如表2所示。

表2　俯仰运动下各支链受力情况

2.3.3横滚运动

驱动支链1、2、3的在X、Y、Z方向的受力情况如图7所示。

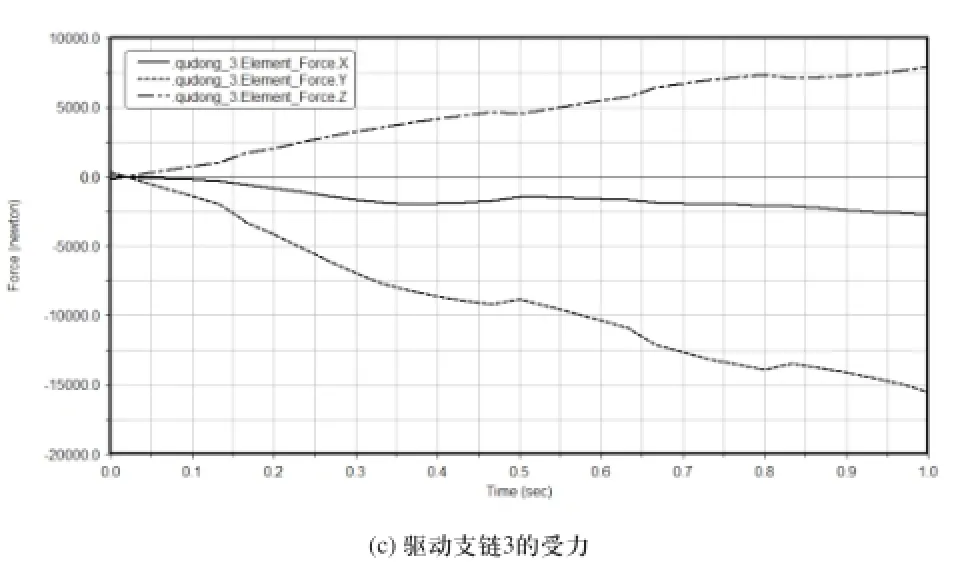
图7　横滚运动驱动支链

从图7横滚运动驱动支链受力仿真结果可以看出，各驱动支链的在沿各个轴线方向的受力曲线图中，沿Y轴方向受力最大，这里给出各驱动支链Y轴的受力数据分析，如表3所示。

表3　横滚运动下各支链受力情况

综上飞行模拟器在三种姿态下模拟飞行的最小承载力为48019.80N，远远大于额定荷载30000N，据此可得所设计的飞行模拟器的承载能力满足技术指标要求。

3　模型结构分析

给飞行模拟器运动平台施加额定的荷载，在三种飞行姿态下，测得各驱动支链的力矩和受力情况，以此来判断模型结构的合理性［15］。

3.1升降运动

由图8（a）支链受力图知飞行模拟器的升降运动在额定荷载下，各驱动支链沿轴线方向受力的数值大小差别很小，没有出现单个支链应力集中的情况。从图8（b）支链转矩图知，各驱动支链在X、Y、Z三个轴线方向所受转矩数值大小差别不大，没有出现单个支链所受转矩数值较大的状况。

3.2俯仰运动

由图9（a）支链受力图知，俯仰运动在额定荷载下，各驱动支链在X、Y、Z轴线方向的受力基本均衡。由图9（b）各支链转矩图知，沿X轴线方向，驱动支链1、3所受转矩数值大小基本均衡，相比之下驱动支链2所受转矩较小；沿Y轴线方向，驱动支链1、2、3所受转矩大小差别不大；沿Z轴线方向，驱动支链1、3所受转矩数值大小基本相等，驱动支链2所受转矩较小。由于俯仰运动姿态的特殊性，模拟飞行器前端先俯后仰，所以出现转矩在驱动支链1、3较大。

3.3横滚运动

由图10（a）支链受力图知，飞行模拟器在额定荷载下，做横滚运动时，各驱动支链所受力沿X、Y、Z轴线受力均衡。从图10（b）支链转矩图可以看出，沿X轴线方向，驱动支链1、2所受转矩数值大小差别很小，驱动支链3所受转矩较小；沿Y轴线方向，驱动支链1、2、3所受转矩数值大小差别不大；沿Z轴线方向，驱动支链1、2所受转矩数值差别很小，驱动支链3所受转矩数值大小较小。由于横滚运动姿态的特殊性，驱动支链1对应运动平台的边先下俯而后上仰，所以出现驱动支链1所受转矩较小。

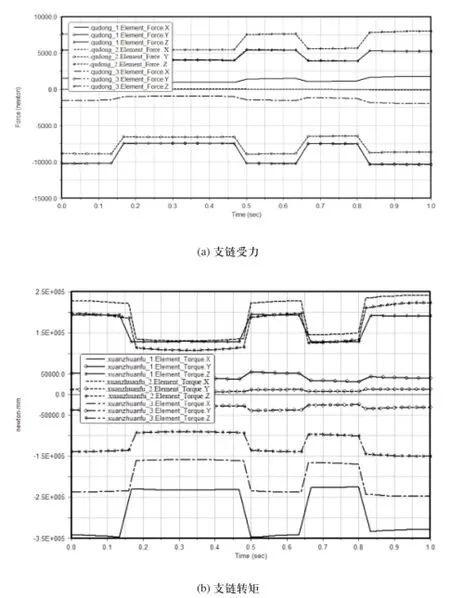
图8　升降运动

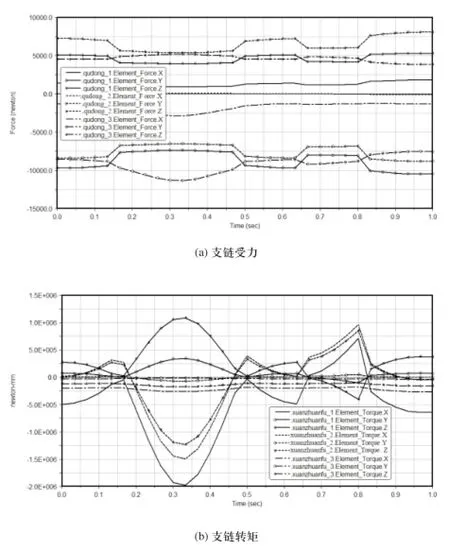
图10　横滚运动

4　结束语

采用Kane的方法建立精确简单的动力学模型，在此模型下，通过UG和ADAMS联合仿真，方便快速地验证了平台的承载能力，简单明了地判断出模型结构设计的合理性。仿真结果表明该飞行模拟器模型结构合理、承载能力足够，满足模拟飞行运动的要求。该研究方法有助于飞行模拟器的设计研发。

【】【】

［1］ 李长春，延皓，张金英，等.一种改进的6自由度运动模拟器逆动力学模型［J］.兵工学报，2009，30（4）:446-450.

［2］ 季晔，刘宏昭，原大宁，等.含驱动摩擦的四自由度并联机构动力学分析［J］.中国机械工程，2012，23（8）:910-914.

［3］ Sanders G H W，Manz A.Chip-based microsystems for genomic and proteomic analysis［J］.TRAC-Trends in Analytical Chemistry，2000，19（6）:364-378.

［4］ 韩佩富，王常武，孔令富，等.改进的6-DOF并联机器人Newton-Euler动力学模型［J］.机器人，2000，22（13）:315-318.

［5］ 王常武，孔令富，韩佩富.改进的6-DOF并联机器人Lagrange动力学模型及其并行处理［J］.计算机工程与应用，2000，（3）:78-79.

［6］ 张国伟，宋伟刚.并联机器人动力学问题的Kane方法［J］.系统仿真学报，2004，16（7）:1386-1391.

［7］ Xuchong Zhang，Xianmin Zhang ，Zhong Chen. Dynamic analysis of a 3-RRR parallel mechanism with multiple clearance joints［J］. Mechanism and Machine Theory，2014，3（5）:105-115.

［8］ 黄真，赵永生，赵铁石.高等空间机构学［M］.北京:高等教育出版社，2006.

［9］ 张策.机械动力学［M］.2版，北京:高等教育出版社，2008.

［10］ 曲展龙.六自由度并联机构的仿真与结构优化［D］.哈尔滨:哈尔滨工业大学，2013.

［11］ 刘显峰.某型战机飞行模拟器三自由度运动平台的设计［D］.哈尔滨:哈尔滨工业大学，2010.

［12］ 苑飞，赵铁石，赵延治.并联机构承载能力分析［J］.中国机械工程，2015，26（7）:871-877.

［13］ Jian-jun Bu，Xing-bo Wang. ADAMS Modeling and Dynamics Simulation of Mosaic Particle’s Motion State［J］.IEEM ，2014 （10）:239-244.

［14］ 刘彦武，孙立宁，曲东，等.基于ADAMS的并联机器人承载能力仿真［J］.制造业自动化，2007，29（7）:79-81.

［15］ 徐炜.基于Pro/E和ADAMS的三自由度运动平台仿真分析［J］.现代制造工程，2010（8）:69-72.

Analysis and simulation of dynamics model for 3-DOF flight simulator

TH12

A

1009-0134（2016）06-0097-07

2016-02-11

国家自然科学基金面上项目（51175321）；教育部人文社会科学研究专项任务项目（15JDGC017）

韩红伟（1990 -），男，河南驻马店人，硕士研究生，研究方向为飞行模拟器运动平台运动学和动力学仿真、CAD/CAM在机电产品中的应用。