基于Matlab和lingo对生产过程中机器设备布局的优化
2016-08-23张广铖
张广铖
基于Matlab和lingo对生产过程中机器设备布局的优化
张广铖
(南京农业大学 工学院,南京 210031)
现下很多工厂生产产品时,不同的生产线共用同一组机器设备很是常见,不同生产线下所需机器加工的顺序不尽相同,因此合理布局一组机器设备,是减少加工过程物料搬运步数的关键。本文针对线图模式下的机器设备布局,利用matlab程序和lingo算法,求解出最佳的布局方式,有一定的推广意义。
布局优化 最小步数 matlab lingo
引言
现今大多数的工厂中,一组机器设备会负责生产几条甚至更多的生产线。这样的生产方式原因来自于两方面,第一,可以增加机器的工作效率,降低其闲置率;第二,节约企业成本。这样的生产方式固然可降低成本,但随之带来的是生产线之间存在等待时间,物料搬运复杂度变高,导致生产效率降低和物料搬运成本的增高。那么如何在机器设备少的情况下,减少其物料搬运成本,使成本达到最低?本文针对一个具体实例,用matlab和lingo对其布局进行分析,合理安排机器设备的位置,使物料搬运成本最低。一组零件及其生产流程如表1所示,每个机器设备之间距离为1,试给出较合理布局。
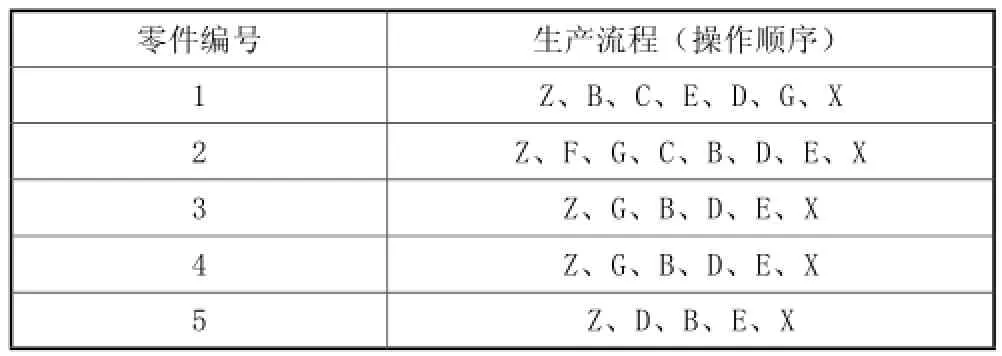
表1 零件及其生产流程的布局
1 基于matlab程序对生产流程的优化
对于上述的问题,5个零件工序,都是从Z开始,至X结束。可将Z看做原材料入口,X看做生产线出口,其中B、C、D、E、F、G看做不同的机器设备。进一步分析可知,要使搬运步数最少,即为各个零件工序各个加工步骤总步数最少,所以将中间6个机器设备看做变量随机排序,6个变量的取值为2,3,4,5,6,7中的一个且各不相等,以此法排列,共有66A种,即720种排序方式。第一道工序Z赋值为1,最后一道工序X赋值为8,共同赋给一个720×8的矩阵,这个矩阵包含了所有的机器设备排列,之后用一个for循环,求出所有可能情况下的步数。matlab程序如下:

end
zuijia=min(ss)
上述程序中分别将Z、B、C、D、E、F、G、X分别看作是变量a1、a2、a3、a4、a5、a6、a7、a8,其中a1、a8分别为常量1和8,程序中的变量lujing代表最短路径时B、C、D、E、F、G在最佳排列方式下的位置,变量qq则为最佳排列方式,变量zuijia为最佳排列时的总步数。
最后得到结果:
zuijia=51,qq='Z''F''G''C''B''D''E''X'。
2 基于lingo算法对生产流程的优化
Lingo算法的思想与上述所说的matlab思想相同,以5个零件的生产步数为目标函数,以6个变量的取值为2,3,4,5,6,7中的一个且各不相等为约束条件,lingo算法如下:

min=@a b s(a(1)-1)+@a b s(a(2)-a(1))+@ abs(a(4)-a(2))+@abs(a(3)-a(4))+@abs(a(6)-a(3))+@ abs(8-a(6))+@abs(a(2)-1)+@abs(a(4)-a(2))+@ abs(a(3)-a(4))+@abs(a(1)-a(3))+@abs(8-a(1))+@ abs(a(5)-1)+@abs(a(6)-a(5))+@abs(a(2)-a(6))+@ abs(a(1)-a(2))+@abs(a(3)-a(1))+@abs(a(4)-a(3))+@ abs(8-a(4))+@abs(a(6)-1)+@abs(a(1)-a(6))+@ abs(a(3)-a(1))+@abs(a(4)-a(3))+@abs(8-a(4))+@ abs(a(3)-1)+@abs(a(1)-a(3))+@abs(a(4)-a(1))+@ abs(8-a(4));
@for(bushu(i):a(i)=@sum(zhi(j):credit(i,j)*fla g(i,j)));
@for(zhi(j):@sum(bushu(i):flag(i,j))=1);
@for(bushu(i):@sum(zhi(j):flag(i,j))=1);
@for(links:@bin(flag));
end
上述lingo程序中a(1)、a(2)、a(3)、a(4)、a(5)、a(6)分别表示B、C、D、E、F、G在最佳排列方式下的位置,credit为位置矩阵,flag为0-1矩阵。最终结果为
a(1)=5,a(2)=4,a(3)=6,a(4)=7,a(5)=2,a(6)=3,即B位于第五个位置,C位于第四个位置,D位于第六个位置,E位于第七个位置,F位于第二个位置,G位于第三个位置,最后的排列顺序额为Z―F―G―C―B―D―E,目标函数的值为51,和matlab结果相同。
3 模型的推广
本文中所介绍的matlab程序和lingo算法,只针对于同一条直线上的机器设备布局优化,在此基础上,不论生产线条数的多少,机器设备的多少,均适用,具有一定的推广意义。
[1]刘佳.大学数学教学中MATLAB的应用[J].常州信息职业技术学院学报,2011,10(6):67-70.
[2]管梅.LINGO在运筹学实践教学中的应用[J].科技视界,2015,(12):19-20.
Matlab and Lingo of the Production Process Optimization Based on Equipment Layout
ZHANG Guangcheng
(Nanjing Agricultural College Institute of Technology,Nanjing 210031)
Holding many lessons when many factories producing products, different production lines share the same set of equipment is very common, the order required for machining in different production lines are not the same, so a group of rational distribution of equipment, material handling process is key to reducing the number of steps . In this paper, machinery and equipment layout diagram mode, using matlab procedures and lingo algorithms for solving the optimal layout, there are some promotional sense.
layout optimization, the smallest number of steps, matlab, lingo
