基于RD－RISR的单基地MIMO雷达DOA估计方法

党晓方 张 辉

(1.西安电子工程研究所西安710100;2.陆航军代局驻西安地区军代室西安710065)

信号数据处理

基于RD－RISR的单基地MIMO雷达DOA估计方法

党晓方1张 辉2

(1.西安电子工程研究所西安710100;2.陆航军代局驻西安地区军代室西安710065)

针对单基地MIMO雷达的到达角估计，提出了基于迭代最小均方差准则的降维重复迭代超分辨算法。首先利用降维矩阵将高维接收数据降维，然后利用重复迭代超分辨算法估计目标角度。该算法在不需要提前估计目标数，在少快拍情况下估计性能并未出现明显下强，在相干目标的情况下(如多径)可能很好的估计目标数目与角度，仿真结果验证了本文所提算法的有效性。

MIMO雷达;降维;重复迭代;超分辨

0 引 言

MIMO雷达［1］起源于MIMO通信系统，其利用多个发射天线同时发射相互正交的信号，在接收端利用多个接收单元接收目标回波信号。与相控阵雷达相比，MIMO雷达具有更好的参数分辨力［2］，更高的自由度［2］以及角度估计精度等优点［3］。根据雷达布阵方式的不同，MIMO雷达可以分为分布式［3，4］与单基地两种模式［5］:分布式雷达发射天线与接收天线间隔较远，可以有效的克服目标RCS闪烁;而单基地MIMO雷达发射阵与接收阵相隔较近，相对于目标的角度是相同的，根据发射阵子与接收阵子间的相位差，单基地MIMO雷达可以形成一个虚拟的长孔径阵列，从而得到窄带宽，低旁瓣，高角度分辨力与角度估计精度的优点［5，6］。

现有的MIMO雷达的角度估计算法很多。针对双基地MIMO雷达，文献［7］中提出两维Capon算法估计目标的波离角与波达角;为了降低运算量，文献［8］提出了一种多项式求根算法;文献［9］与［10］分别提出了2维MUSIC算法与降维MUSIC算法;为了进一步降低算法运算时间，文献［11］提出了利用ESPRIT算法估计目标角度。

然而，上面所提算法都要首先估计目标数目，然后利用接收数据估计数据协方差矩阵，再进行特征值分解，最后估计目标的角度参数。当目标的角度随时间变化较快，可用的快拍书就会减少，这样估计的数据协方差矩阵就不准确，最终导致目标角度信息的不准确;特别当在相干目标情况下，上面所提算法就会失效。针对以上缺点，本文提出一种降维重复迭代超分辨算法，该算法不需要估计数据协方差矩阵以及特征值分解，可以实现目标数，角度与幅度的同时估计，同时该算法在多径条件下仍然能够取得良好的表现。

1 单基地MIMO雷达信号模型

考虑一个单基地MIMO雷达，其发射阵列是阵元数为的均匀线阵，阵元间距为半波长，接收阵列的阵元数为，亦为距为半波长的均匀线阵，接收阵列和发射阵列放置的足够近，使得对于远场目标而言，目标的波离方向DOD和波达方向DOA是相同的，在阵列远场同一距离单元有个目标。如图1所示。

图1 单基地MIMO雷达天线位置示意图

这样，在接收端匹配滤波器的输出信号可以写成［7］

其中αk是第k个目标的复幅度;αt(θk)=［1 e－jπsinθk…ej(M－1)πsinθk］T∈CM×1和 αr(θk)=［1

ejπsinθk…ej(N－1)πsinθk］T∈CN×1分别是第 k个目标的发射和接收导向矢量;S∈CM×N是发射的正交信号，N∈CN×N是高斯白噪声。由于发射信号是正交的，所以在接收端可以用SH对接收信号进行匹配滤波，这样，输出信号就可以表示为［12］

其中珚N=NSH为噪声项。假设接收和发射导向矢量在L个快拍内是不变的，这样多个快拍的接收信号可以写为

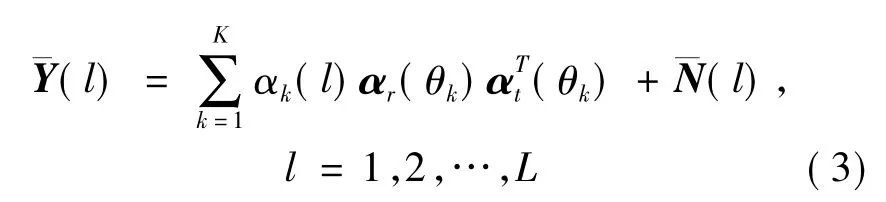
将珔Y(l)按列依次排列，可以将式(3)中的接收矩阵矢量化为如下形式

其中g(θk)=αr(θk) αt(θk)∈CMN×1为发射－接收合成导向矢量。

2 基于RD－RISR算法的角度估计

由文献［13］可知，发射－接收合成导向矢量g

(θ)中仅仅有M+N－1个不相同的元素:［1

ejπsinθk…ej(M+N－1)πsinθk］∈C(M+N－1)×1，所以 g(θ)可以重新写成这M+N－1个不同元素的线性组合

其中 b(θ)=［1 ejπsinθk…ej(M+N－1)πsinθk］T是一个M+N－1维的Vandermonde矢量，T是一个MN ×(M+N－1)维的变换矩阵:

将式(5)代入式(4)后，接收信号可表示为

从式(7)可以看出，接收信号 珔Y(l)中的目标信号位于由Tb(θk)张成的低维信号空间。因此，可以将高维的接收数据转化至该低维空间，然后再估计目标角度。定义D为降维矩阵，此时接收数据重新写为如下形式:

其中span{D}=span{T}，即由D展开的空间与T展开的空间是相同的。注意到额外的噪声项N(l)变为DHN(l)，为了保证DHN(l)仍然是一个均值为0，方差矩阵为σ2IM+N－1的高斯白噪声，将D构造为［13］

将式(9)代入式(8)，可以得到

注意到b(θ)=［1 ejπsinθk…ej(M+N－1)πsinθk］T是由目标的角度信息θ和降维后的阵列个数M+N－1共同决定的，而从式(10)中可以看到，目标角度的估计可以看成是在第l次快拍下对K个目标在θ空间下的定位。这个过程可以通过将接收数据Y珘(l)近似参数化完成，如:

其中，B是一个(M+N－1)×Q维的矩阵，通常情况下Q远远大于M+N－1，其是由b(θ)构造而成的，形式如下

其中Q的含义是将整个θ空间平分为Q等份，即将2π量化为Q个离散量，相邻等份的角度间隔为θΔ=2π/Q。很明显，为了得到更好的角度估计精度，就需要对2π更细致的量化，意味着需要Q更大。在式(11)中，α(l)是矩阵B中Q个导向矢量的复幅度矢量，其维数为Q×1。比较式(10)与式(11)，可以看到，如果对θ空间量化的足够细致，α(l)会仅仅在K个目标所在的角度处不为0，而在其他位置处均为0。因此，目标的角度估计问题就转化为搜索矢量α(l)的峰值位置。在这里注意到，对于MUSIC和ESPRIT算法，目标的个数需要在处理之前通过其他方法估计，而该算法下目标的数量仅仅需要通过确定α(l)的峰值个数就可以获得，而且，峰值的幅度就是目标回波的幅度。

对α(l)的估计可以转化为最小化如下最小均方差

其中W(l)为一个(M+N－1)×Q维的最小均方差匹配滤波器组。通过式(13)可以得到W (l)的形式如下

假设目标回波和噪声是统计独立的，将式(11)代入式(14)可以得到

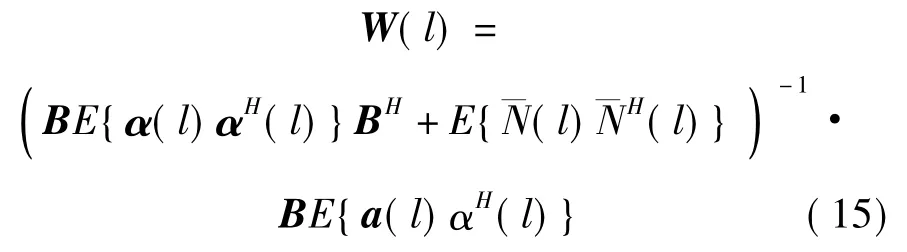
在式(15)中，E{珚N(l)珚NH(l)}为噪声协方差矩阵，定义为R，注意到，噪声的方差为σ2，所以可以简化为R=σ2I;而对于信号相关项BE{α(l)αH(l)}BH，假设 中各个元素都在时间上是不相关的，这是由于RD－RISR算法在本质上是对每个快拍数据进行独立处理，所以该算法并不关心目标在时间上是否相关，因此与子空间类算法不同，RD－RISR算法也可以估计相关目标的角度。为了保证α(l)中各个元素都在时间上是不相关的假设，空间谱分布矩阵可以定义为如下形式

其中P(l)的对角元素组成了空间能量分布谱，IQ×Q是一个R=σ2I维的单位阵。将式(16)和代入到式(15)中可得

注意到上式中P(l)是未知的，在迭代过程中需要对P(l)求得一个初始值，而P(l)的形式可以看到要得到其初始估计，就要求对α(l)进行初始估计，而α(l)的初始估计可以通过将量化后的接收信号与一个匹配滤波器组相乘得到，在这里，导向矢量矩阵B可以作为该匹配滤波器组，这样就可以得到

因此，P(l)的初始估计如下

然后根据式(20)得到第i次 的最小均方差估计

根据式(21)得到的第i次估计

式(19)、(20)和(21)构成了RD－RISR算法的第i次迭代的基本形式。当迭代够事先决定的次数或者时，整个迭代过程停止，其中 ε为事先定义的极小值。这时的对角元素就是RD－RISR谱，给出了K个目标的幅度和角度信息。

前面所有的讨论均是在单次快拍的情况下讨论的，然而，当目标的功率谱分布在给定的时间内是不变的时，RD－RISR同样也可以处理多个快拍数据。同时实验表明多次快拍下的估计性能要比单次快拍下好的多。

当目标的功率谱分布在L个快拍数据内是不变的时候，可以用一个总的匹配滤波器组对L个快拍的接收数据+l－1)］处理，得到

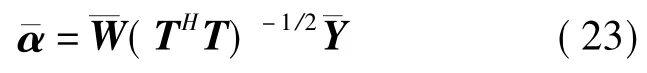
在第i次迭代中，用式(24)中的平均功率估计代替式(20)中的，然后求得第i次总最小均方差滤波器组而式(17)中最初的滤波器组依然是矩阵B。可以看到单个快拍下的RDRISR算法其实是多次快拍下额特例，在下面的讨论中，该算法均是对L个快拍数据进行处理。

为了方便，RD－RISR的角度估计步骤如下: 1.用SH对接收信号进行匹配滤波，得到数据矢量

4 计算机仿真

仿真中单基地MIMO雷达的发射阵列与接收阵列均为间距半波长的等距线阵，M=N=10。其测角的均方根误差表示如下

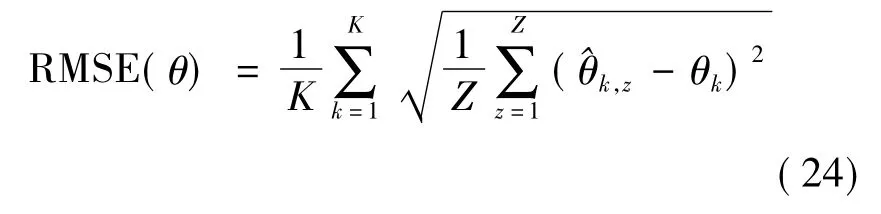
其中Z为MonteCarlo次数，^θk，z为第K个目标角度θk的第z次估计。

仿真1 算法收敛性验证

本仿真中考虑两个非相关目标，目标一的角度为θ1=10°，信噪比SNR=20 dB，目标二角度为θ2=14°，信噪比SNR=10 dB;快拍数L=5，角度空间量化量Q=3600。图2分别给出了初始的，经过2、10和17次迭代的RD－RISR谱。从图中可以看出经两次迭代之后RD－RISR谱的旁瓣基本被消除，并且大概可以看到两个目标;经过10次迭代之后两个目标已经可以清晰的分辨出来;经过17次迭代之后，RD－RISR谱仅仅在目标所在的角度处是非0值，这说明在没有目标个数的先验信息下，RD－RISR谱中非零值的个数就是目标的个数，在对角度估计的同时也完成了对目标个数的估计。并且，可以观察到目标的幅度也分别是真实的20dB和10dB。

图2 RD－RISR算法收敛性

仿真2 分辨率与角度估计精度验证

仿真条件如仿真1，不过在仿真2中快拍数L分别为2、3、5、8和10，为了不将错误的测角信息也进行比较，所以在做测角精度仿真的同时也要做分辨率的仿真，仅仅当成功分辨之后才将测角结果记入RMSE估计。由图3可以看到，在同信噪比下，随着快拍数的增多，RD－RISR算法的分辨率会变好，特别可以看到当快拍数从2到3时，算法的分辨率有了明显的提升。而从图4中可以看到，在同信噪比下，随着快拍数的增多，目标的测角精度也随之提高，同时也可以看到，当SNR＞15dB时，快拍数L等于5、8和10的性能相同，而且不再降低，这是由于测角精度的下限受到角度量化值Q的限制，其无法突破2π/Q。

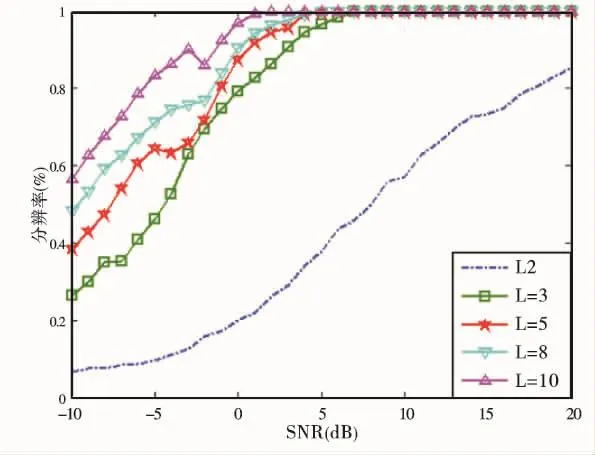
图3 分辨率随SNR变化图

图4 角度估计RMSE随SNR变化图

仿真3 相关源估计能力验证

在本仿真中，假设有三个相关源，其角度分别为θ1=－10°，θ2=10°和θ3=15°，信噪比SNR= 10dB，快拍数L=5。在图5中，同时给出了RDMUSIC谱和 RD－CAPON谱用以比较算法性能。从图中可以看到由于相关源的存在，RD－MUSIC和RD－CAPON算法并不能分辨出三个目标，这是由于三个目标的特征值相同，导致数据协方差矩阵是秩亏损的，而RD－RISR算法可以清楚的分辨出三个相关源的位置与幅度。图6给出了当目标相关时不同快拍下目标角度估计精度随SNR的变化图，如同非相关目标，在相同信噪比下，随着快拍数的增加，RD－RISR算法的测角精度也随之提高，在低信噪比和少快拍数的情况下，目标的估计精度也是可以得到保证的。

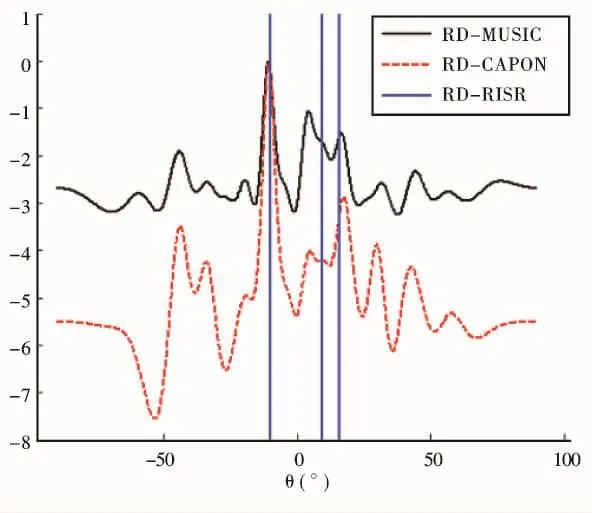
图5 相关目标算法谱图

图6 相关目标角度估计RMSE随SNR变化图

图7 角度估计RMSE随信噪比变化图

仿真4 角度估计性能比较

目标信息如仿真一，快拍数L=100，角度空间量化量 Q=18000，也就是测角精度的下限为0.02°。从图中可以看到，RD－RISR算法的估计性能优于RD－Capon算法。

3 小 结

本文针对单基地 MIMO雷达提出了 RDRISR算法，该算法在降低计算量的同时，可以对目标的数量、幅度和角度信息同时完成估计，并且该算法可以实现对相关目标的估计，仿真结果验证了算法的有效性。

［1］E.Fishler，A.Haimovich，R.Blum，D.Chizhik，L.Cimini，R.Valen－zuela，MIMO radar:an idea whose time has come，in:Proceedings of the IEEE Radar Conference，Philadelphia，PA，USA，2004，(1):71－78.

［2］I.Bekkerman，J.Tabrikian，Target detection and localization using MIMO radars and sonars，IEEE Transactions on Signal Processing，2006，54(10):3873－3883.

［3］E.Fishler，A.Haimovich，R.Blum，L.Cimini，D.Chizhik，R.Valenzuela，Spatial diversity in radarsmodels and detection performance，IEEE Transactions on Signal Processing 54(3)(2006)823－838.

［4］A.M.Haimovich，R.Blum，L.Cimini，MIMO radar with widely separated antennas，IEEE Signal Processing Magazine，2008，25(1):116－129.

［5］J.Li，P.Stoica，MIMO radar with colocated antennas，IEEE Signal Processing Magazine 24(5)(2007)106－114.

［6］L.Z.Xu，J.Li，P.Stoica，Target detection and parameter estimation for MIMO radar system，IEEE Transactions on Aerospace and Electronic Systems，2008，44 (30):927－939.

［7］H.Yan，J.Li，G.Liao，Multitarget identification and localization using bistatic MIMO radar systems，EURASIP Journal on Advances in Signal Processing，2008，8 (1):283483.

［8］Rong Xie，Zheng Liu，Zi－jingZhang，DOA estimation for monostatic MIMO radar using ploynomial rooting，Signal Processing，2010，90:3284－3288.

［9］Gao，X.，Zhang，X.F.，Feng，G.P.，et al.(2009).On the MUSIC－derived approaches of angle estimation for bistatic MIMO radar.In International conference on wireless networks and information systems，343－346.

［10］Zahernia，A.，Dehghani，M.J.，＆ Javidan，R.(2011).MUSIC algorithm for DOA estimation using MIMO arrays.In 6th international conference on telecommunication systems，services and applications，149－153.

［11］C.Duofang，C.Baixiao，Q.Guodong，Angle estimation using ESPRIT in MIMO radar，Electronics Letters 44(12)(2008)770－771.

［12］H.Lv，D.Feng，H.Liu，Tri－iterative least－square method for bearing estimation in MIMO radar，Signal Processing 89(2009)2686－2691.

［13］L.Xu，J.Li，and P.Stoica，Adaptive techniques for MIMO radar，in:Proceedings of the 4th IEEE Workshop on Sensor Array and Multi－Channel Processing，Waltham，MA，2006:258－262.

RD－RISR－Based DOA Estimation Method of Monostatic MIMO Radar

Dang Xiaofang1，Zhang Hui2
(1.Xi’an Electronic Engineering Research Institute，Xi’an 710100; 2.Xi’an Representative Office of Army Aviation，General Armament Department，Xi’an 710065)

Aiming at DOA estimation of monostatic MIMO radar，a dimensionality reduction repeat iterative superresolution algorithm based on iterative least mean square error criteria is presented.Firstly，high dimension receiving data is reduced by using dimension reduction matrix，then，target angle is estimated by using repeat iterative superresolution algorithm.It is not needed to estimate target number and angle in advance by using this algorithm，the estimation performance is not decreased obviously in condition of absent snapshot，and in condition of coherent target(like multipath)，the target quantity and angle may be estimated favorably.The simulation result verifies effectiveness of the presented algorithm.

MIMO radar;dimension reduction;repeat iterative;super－resolution

TN

A

1008-8652(2016)04-031-06

2016-01-11

党晓方(1987－)，男，博士研究生。研究方向为MIMO雷达。