“概率”中蕴含的数学思想

李先永



思维训练营/思想方法
CHU ZHONG SHENG SHI JIE

“概率”中蕴含的数学思想

李先永

数学的精髓不在于知识本身，而在于数学知识中所蕴含的数学思想方法.数学思想也是知识转化为能力的桥梁.学习概率知识，也要重视数学思想方法的应用.现将初中概率中常见的数学思想举例如下.

一、方程思想

方程思想就是对所求的概率问题通过列方程（或方程组）求解的一种思想方法.

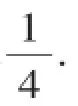
（1）取出白球的概率是多少？

（2）如果袋中的白球有18个，那么袋中的红球有多少个？

【分析】（1）因为取出的球不是白球就是红球，所以P（取出白球）+P（取出红球）=1；

（2）设袋中有红球x个，

解得x=6，

所以袋中的红球有6个.

【点评】利用概率公式建立方程可以求解已知概率而其他量未知的计算问题，这是解决概率问题的常用方法.

二、数形结合思想

“概率”的数形结合主要有：（1）有列表法或画树状图法试验的等可能的结果数；（2）几何图形中概率的问题；（3）结合点所在的象限、函数图像等求概率问题；（4）结合统计图表解决与概率有关的实际问题.

例2如图1，在平面直角坐标系中，正方形ABCD的边长为4.现做如下实验：将转盘划分成4个相同的小扇形，并分别标上1，2，3，4.转动转盘两次，转盘停止后，指针所指向的数字作为平面直角坐标系中点P的坐标（第一次作为横坐标，第二次作为纵坐标），指针如果指向分界线上，则重新转动转盘.

（1）请你用树状图或列表的方法，求P点落在正方形ABCD面上（含内部与边界）的概率；

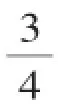
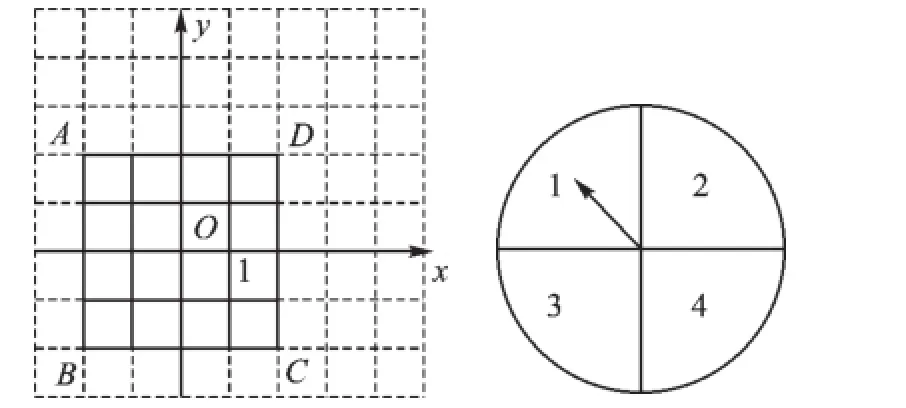
图1

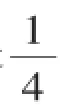
解：（1）列表如下：

1234 1　　（1，1）　　（1，2）　　（1，3）　　（1，4）2　　（2，1）　　（2，2）　　（2，3）　　（2，4）3　　（3，1）　　（3，2）　　（3，3）　　（3，4）4　　（4，1）　　（4，2）　　（4，3）　　（4，4）

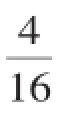
（2）略.

【点评】本题主要考查了概率的计算方法和正方形与平移的有关性质.要会根据正方形的性质得到所对应的点的坐标，利用列表法求符合条件的概率.用到的知识点为：概率=所求情况数与总情况数之比.

三、转化思想

在概率问题中，所有可能结果的概率之和等于1，因此求某个较复杂的随机事件或多个随机事件的概率之和时，可以先求出所有其他事件发生的概率，再用1减去这个概率，即可解决问题.

例3一只不透明袋子中装有两个红球、3个黄球，4个绿球，这些球除颜色外都相同.小明搅匀后从中任意摸出一个球，这个球是红球或绿球的概率是_______.

【分析】摸出的是黄球和摸出的是红球或绿球的概率和为1，所以可以先求出摸出的是黄球的概率，再用1减去这个概率就是摸出的是红球或绿球的概率.

【点评】本题也可以分别求出摸出红球和摸出绿球的概率，再相加便是摸出的是红球或绿球的概率.

四、分类讨论思想

分类讨论思想在概率中的应用，主要体现在将所有可能的情况一一列举出来.

例4某人的钱包内有10元、20元和50元的纸币各1张.从中随机取出两张纸币.

（1）求取出纸币的总额是30元的概率；

（2）求取出纸币的总额可购买一件51元的商品的概率.

【分析】（1）随机取出两张纸币的情形共有3种，即（10，20），（10，50），（20，50），其中取出纸币的总额是30的情况有1种. （2）取出纸币的总额大于51的情况有两种.

解：（1）随机取出2张纸币，共有3种情况，即（10，20），（10，50），（20，50），其中取出纸币的总额是30的情况有1种，

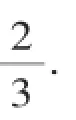
【点评】当符合要求的情形不止一种时，需要应用分类的思想来解答.

（作者单位：江苏省宿迁市宿豫区实验初级中学）