“锐角三角函数”学习要点
2016-08-22王竞进
王竞进
知识学习园/概念透析
CHU ZHONG SHENG SHI JIE
“锐角三角函数”学习要点
王竞进

“锐角三角函数”是初中数学重要内容之一,它揭示了直角三角形边角之间的函数关系.学习本章时,需要抓住以下几个要点.
一、认识四个基本概念
本章涉及的基本概念有正切、正弦和余弦以及解直角三角形.

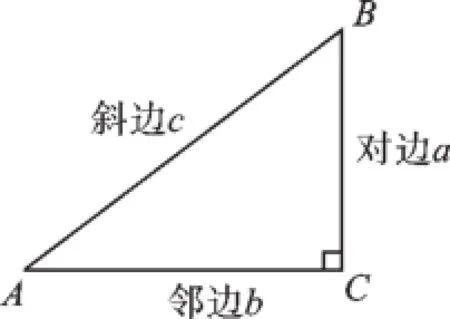
图1



例1(2015·曲靖)如图2,在半径为3的⊙O中,直径AB与弦CD交于点E,连接AC,BD.若AC=2,则cosD=_______.
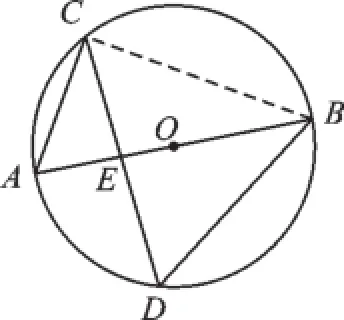
图2
【解析】连接BC,
∵AB为直径,
∴∠ACB=90°,
∵∠D=∠A,
【说明】本题应用圆周角的性质将∠D转化为∠A,使其转化到直角三角形ABC中,再应用余弦的概念求得结果.
由直角三角形的边、角中的已知元素,求出所有边、角中的未知元素的过程,叫做解直角三角形.在直角三角形中,除直角外的5个元素,至少知道包含1条边的两个元素就可以确定直角三角形中其余未知元素的值.
例2如图3,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC平分线,AD=20.求AB的长.

图3
【解析】∵在Rt△ABC中,∠C=90°,∠A=30°,∴∠ABC=60°.
∵BD是∠ABC平分线,∴∠DBC=30°,
∴∠BDC=60°,∠ABD=∠A=30°,
∴BD=AD=20.
∵在Rt△DBC中,
【说明】本题借助锐角三角函数的概念,使问题化归到直角三角形中,应用直角三角形的边角之间的函数关系,根据问题中的已知元素求得未知元素.
二、熟记三个特殊值
利用特殊的等腰直角三角形和含有30°角的直角三角形的性质,我们可以求得30°、45°、60°的三角函数值(如下表).
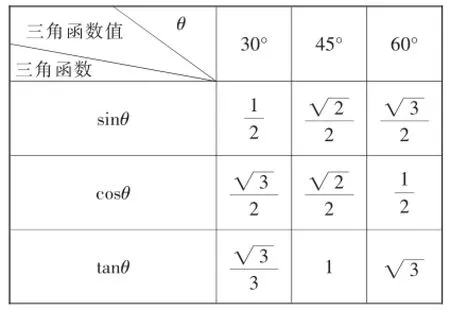
从表格中我们可以发现:sin30°、sin45°、sin60°值的分母都是2,分子可以看成是,正弦值随角度的增大而增大;cos30°、cos45°、cos60°值的分母都是2,分子可以看成是,余弦值随角度的增大而减小;tan30°·tan 60°= tan45°=1,正切值随角度的增大而增大.
∴α=30°,β=45°,
∴α+β=75°,所以本题答案为75°.
【说明】本题是一道考查同学们对特殊角的三角函数值和非负数的性质掌握的问题,解答这类问题,需要同学们熟练掌握特殊角的三角函数值.
三、掌握锐角三角函数解决实际问题
解直角三角形的知识广泛应用于测量之中,主要用于计算距离、高度和角度.
例4(2015·衡阳)如图4,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米到达F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为().

图4
【解析】根据题意可知:
∠ACE=30°,∠AEG=60°,CE=DF=100(米).
我们不妨设EG=x米,在Rt△AEG中,
∵∠AEG=60°,
在Rt△ACG中,
∵CE=DF=100,
∴x+100=3x,解得x=50,
(米),所以本题答案为C.
【说明】本题以测电视塔的高度为背景,考查解直角三角形的应用能力,求解时抓住图形中两个直角三角形的公共边建立相等关系式是解题的关键.
例5(2015·遵义)如图5,是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4米,AB=6米,中间平台宽度DE=1米,EN、DM、 CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31° ≈0.86,tan31°≈0.60)
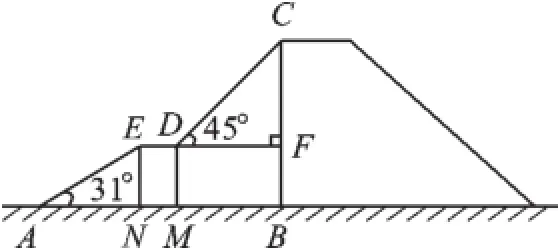
图5
【解析】设BM为x米,则DF=BM=x.
∵Rt△CFD中,∠CDF=45°,
∴CF=DF·tan45°=DF=x,
∴BF=BC-CF=4-x,
∴EN=BF=4-x.
∵Rt△ANE中,∠EAN=31°,
∵AN+MN+BM=AB,MN=DE=1,
答:DM和BC的水平距离BM的长度约为2.5米.
【说明】本题是一道典型的解直角三角形的应用问题,需要把实际问题转化为数学模型来解决.解决与直角三角形有关的应用题最常用的方法是作垂线,构造直角三角形,根据所给数据,选用恰当的三角函数求出有关的量或用含有未知数的式子表示有关的量进行求解.
(作者单位:江苏省建湖县汇文实验初中教育集团汇文校区)
