随机市场需求下双重易逝性产品的回收再造决策研究

曹 裕，郑其昀

(中南大学 商学院，长沙 410083)



【经济学研究】

随机市场需求下双重易逝性产品的回收再造决策研究

曹 裕，郑其昀

(中南大学 商学院，长沙 410083)

闭环供应链；双重易逝性产品；随机需求；消费认可差异

以闭环供应链为研究基础，在兼顾考虑回收价值的时间变化和消费者认可差异的情况下，探讨双重易逝性的产品在随机市场需求中的经营再造决策。研究得出：无论在何种情况下，企业的回收率都与回收规模参数成反比，与再造品节余成本成正比；随着再造品认可度的提升，企业的利润越大，回收力度越大，但最优回收时间却越来越晚。

易逝品(perishable goods)，一般指具有很强时效性的产品，由于其本身的特性和消费者的偏好，通常具有较短的销售周期，未售出产品则会失效或价值大打折扣，例如牛奶，报纸，机票等。一方面来说，随着一些高科技产品生命周期越来越短，更新换代越来越快，表现出易逝品的特性，例如手机和电脑等；另一方面，企业实行可持续发展，建立正向物流和逆向物流结合的闭环供应链，使得回收问题尤其是含有丰富科技元素和珍贵材料的高科技产品的回收受到重视。但是由于废旧产品的可利用价值会随时间迅速衰减，如果不能及时回收，则会丧失大部分再造价值，只剩下原材料残值。我们将这种在销售阶段和回收阶段都呈现出易逝特性的产品，称为双重易逝性产品(double-perishable goods)，也是本文研究的对象。

现有的关于废旧产品回收的模型研究一般都将废旧品的回收价值设为定值，没有考虑到现实状况下废旧产品的时间敏感性；个别研究虽考虑到了此点，但是仅从回收这一个阶段来构建企业的成本最小化模型，很少将销售阶段和回收阶段联合在一起考虑，无法给予企业更加完整和完善的决策建议。

本文尝试性地将销售阶段与回收阶段结合在一起，考虑回收的时间因素和消费者认可差异，研究企业面对随机市场需求该如何决定新产品的产量与定价，当新产品销售之后的一段时间，市场上开始出现废旧的该类产品，这时企业又应该如何通过选择恰当的回收时点和回收努力来决定再造品的数量与价格，通过数学建模的方法将这些复杂的关系一一表示出来，并以利润最大化为导向，为企业提供更加完善详尽的最优决策建议。本文从回收时间和消费者认可度这两个维度对制造企业的最优决策展开探究，同时考虑到了产品销售时和产品回收时的价值衰减性，并给出了计算公式。研究表明：(1)无论在何种情况下，企业的回收率都与回收规模参数成反比，与再造品节余成本成正比；(2)随着再造品认可度的提升，企业的利润越大，回收力度越大，但最优回收时间却越来越晚；(3)通过仿真计算验证结论的正确性。

1 问题描述和模型说明

双重易逝性产品在销售阶段和回收阶段都表现出价值易逝的特性，如果不能及时销售或者回收，都将只剩下原料残值。设产品的生命周期为T，初始企业以Pn的单价销售新产品，单位成本cn为，产量为Qn，市场需求为Dn。当市场上出现废旧或损坏的该类产品时，企业选定t时间(0≤t≤T)开始回收，回收努力系数为e，最终回收率为r，回收的产品用来再造，成本为Cr(再造品的成本节余Δ=cn-cr>0)，再造品以Pr的单价销售，产量为Qr，市场需求为Dr。此外，sn代表新产品单位残值；sr代表再造品单位残值；hn代表新产品单位缺货成本；hr代表再造品单位缺货成本；Π代表利润。其中，Pn，Pr，e，t，r为模型的决策变量，Π为目标函数。

假设 1 双重易逝性产品的生命周期为T，无论是新产品还是再造品在生命周期结束之后都被市场所淘汰，仅存原材料残值。

如果新产品和再造品认可度一致时，产品的总需求量也设为Dn，且此时根据线性的售价与需求量的关系来设定总需求量的表达式为：D=Q-pn。

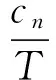
假设4 参考Porteus和Zhou的设定，e表明企业为回收产品做出的努力程度，此时回收成本为ke2，k代表大于零的规模参数。本文假定回收价格比较稳定，主要通过回收努力来影响回收数量。

假设5 无论是Minner等认为废旧产品是服从均匀分布的回收问题，还是Van等认为废旧产品的回收服从齐次泊松分布，都可以得出回收量是随回收时间增长的结论，故本文假设随着时间的流逝，相同努力系数能够回收到的废旧品数量是递增的，即回收率是回收努力和回收时间的增函数，又假设废旧产品回收利用率为100%，故回收量等于再造品产量，并且假设模型为简单的线性结构：Qr=(at+1)eQn,a为大于零的常系数，(at+1)e即为最终回收率，用r来代表最终回收率，且满足0≤(at+1)e=r≤1。

假设6 新产品和再造品制造速度趋于无限大，不考虑库存成本、运送时间等因素。

2 模型构建

2.1 不考虑时间和消费者认知差异的模型构建

企业在生产新产品和回收再造的过程中，新产品与再造品的性能、售价和消费者的认可程度都是相同的，所以企业只需要确定一个售价、回收努力和产量就可以了。此时，需要将废旧产品的回收易逝性也考虑到方程中，故企业的最终利润公式为：

(1)

式(1)中第一行公式代表过量生产情况下的收益，第二行公式代表缺货情况下的收益，第三行是回收努力成本，其中回收废旧产品而节约的总成本为rQnΔ，将节约的总成本分配到每个产品上，就会得到每个产品实际的平均生产成本，即为cn-rΔ，所以每个产品的收益为Pn-cn+rΔ。

2.2 考虑时间因素但不考虑消费者认知差异的模型

当企业开始考虑废旧品的价值和回收率的时间变动时，此时企业的最终利润公式变为：

(2)

式(2)中第一行公式代表过量生产情况下的收益，第二行公式代表缺货情况下的收益，第三行是回收努力成本，因为根据假设3，废旧品的衰减率为cn/T，当企业在t时开始回收时，废旧品仍然剩余的价值为cn(T-t)/T，从t时开始回收直到T时生命周期为止，用平均值来衡量废旧品的价值，即为cn(T-t)/2T，又回收率的表达为r=e(at+1)，所以得到了在考虑时间情况下产品的收益公式Pn-cn+e(at+1)cn(T-t)/2T。

2.3 考虑消费者认知差异但不考虑时间因素的模型

新产品和再造品虽然有时功能无差异，但是消费的心理认知程度还是有很大不同的，这就导致新产品和再造品得分开定价，同时还得考虑两者的替代作用和不同的需求情况，所以在不考虑时间因素的情况下，企业的最终利润公式为：

(3)

式(3)中第一行和第三行公式分别代表新产品和再造品过量生产情况下的收益，第二行和第四行公式分别代表新产品和再造品缺货情况下的收益，第五行是回收努力成本。因为新产品和再造品需要分开定价和预估需求量，所以不能采用上述平均成本思想来建模。

2.4 考虑消费者认知差异和时间因素的模型

跟2.2的情况一致，企业需要考虑回收率随时间的变化和废旧品的衰减情况，这里引入了不同认可度的新产品和再造品，情况就变得更加复杂，所以企业的最终利润公式为：

(4)

式(4)中第一行和第三行公式分别代表新产品和再造品过量生产情况下的收益，第二行和第四行公式分别代表新产品和再造品缺货情况下的收益，第五行是回收努力成本。

公式中同样采用平均生产成本思路来计算跟时间变化有关的再造品成本。当企业t时刻开始回收时，此刻的废旧品剩余的回收价值为cn(T-t)/T，平均节余成本为cn(T-t)/2T，将原成本减去节余的生产成为即为再造品的平均制造成本，即为cn-cn(T-t)/2T，所以经化简，再造品的收益公式为Pr-cn(T+t)/2T。

3 结果探究

结论1 对于企业的最大利润和各变量的最优解，可以通过KKT条件给出结果，但无明确的公式解，只能通过模型仿真来计算与验证。

证明 根据企业的最终利润公式(4)可以得出相应的海塞矩阵，这是一非常复杂的5×5矩阵，但是此海塞矩阵中含有决策变量，故无法作为判断式(4)是否有最优解的充分条件，只能作为最终解的验证条件，而现在一般的数学软件都可以直接判断出解是否是最优解，因此，本文不再单独讨论海塞矩阵。而是根据公式(4)和其约束条件得出拉格朗日乘式：

KKT优化条件如下：

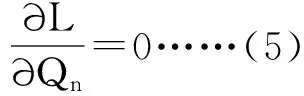
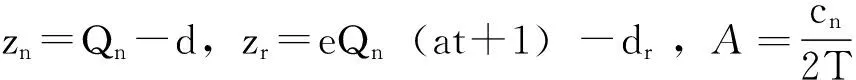
联立式(5)-(10)，可以解得各决策变量的最优解，但由于非线性规划相当复杂，无法用公式表达出结果，因此下面用四组算例给出最优数值结果。

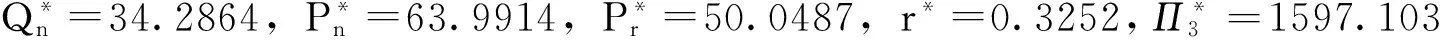
结论2 在保证利润公式有最优解的情况下，企业的回收率都与规模参数k成反比，与再造品节余的成本Δ成正比。

证明 因为本文研究的是非线性规划问题，很难求得解析解，因为无法给出回收的临界值分析，只能进行趋势分析。

对于上述研究的四种情况，由于式(2)和式(4)是将回收率分析成两个变量来研究的，不利于结果讨论，本文只讨论式(1)和式(3)，且这两种情况参数设定与(2)(4)是一致的，讨论的结果也是具有代表性的。

针对式(1)进行关于回收率r的求导，得：

针对式(3)进行关于回收率r的求偏导，得：

结论3 消费者对新产品的认可程度越高，企业的利润越大，回收力度越大，但回收时间却越来越短。

证明 本文对式(4)进行讨论分析，是因为在(4)的情况下，考虑的条件最为全面，能够提供更加详尽完整的参考建议。本文用数值仿真的方法Lingo软件进行计算。

算例如下：令x与y均服从在(0，4)上的均匀分布，k=120,α=3,T=10,hn=sn=6,hr=sr=2,Q=100,cn=25，结果如表1所示。

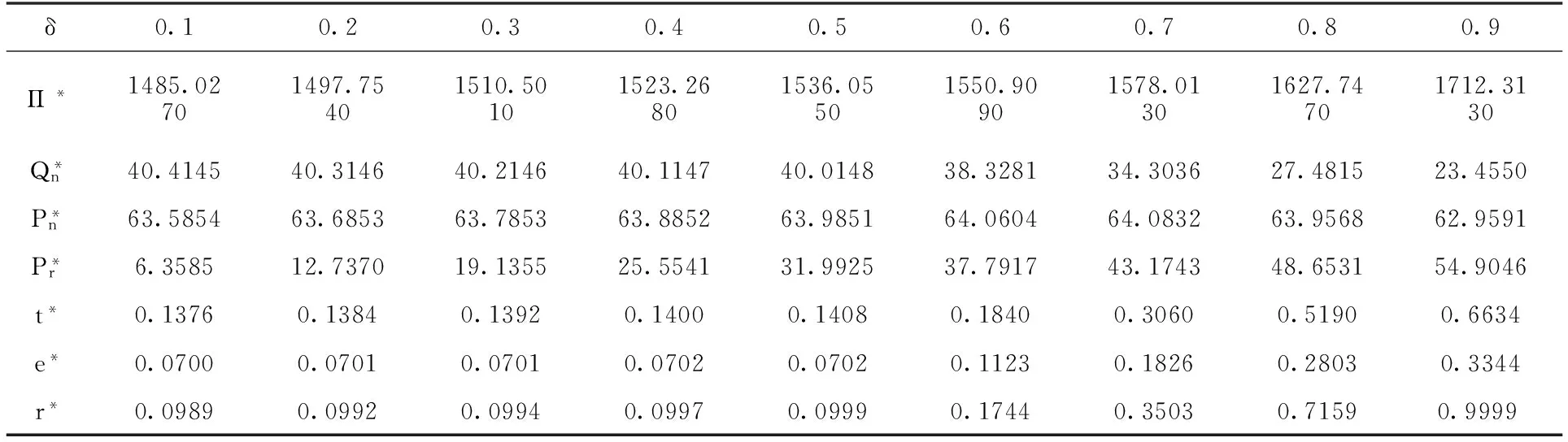
表1 再造品不同的认可度对企业各个变量的影响分析

根据上表的结果显示：①消费者对再造品的认可度越高，企业回收率越高，利润越大；②同时，新产品售价会略微上下浮动，变化不显著，而再造品的售价却随着认可度上升而显著提高；③企业新产品产量显著下降，但销售规模(新产品和再造品的总销售量)却有所上升；④值得注意的是，再造品的认可度越高，企业就越应相对晚些实行回收策略，而不是越有价值就越早回收，这对企业成本不一定有利。这是由于虽然损失部分回收价值，但在回收率上有所提高，这样企业可以通过回收再制造而出售更多的再造品，从而获得利润。所以，对于企业回收来说，如果再造产品的认可度比较低，企业应该更关注回收的可用价值，而如何再造品的认可度非常高，企业应该更关注回收的数量，这样才能获得最高收益。

[1] 计国君,黄位旺. 回收条例约束下的再制造供应链决策[J].系统工程理论与实践,2010,30(8): 1355-1362.

[2] Guide V D R,Souza G C,Van Wassenhove L N,et al. Time value of commercial product returns [J]. Management Science,2006,52(8): 1200-1214.

[3] Porteus E. Optimal lot sizing,process quality improvement and setup cost reduction [J]. Operations Research,1986,34(1): 137-144.

[4] Zhou S X,Yu Y. TECHNICAL NOTE—optimal product acquisition,pricing,and inventory management for systems with remanufacturing [J]. Operations research,2011,59(2): 514-521.

[5] Minner S,Kleber R. Optimal control of production and remanufacturing in a simple recovery model with linear cost functions [J]. OR-Spektrum,2001,23(1): 3-24.

[6] Van Der Laan E,Salomon M,Dekker R,et al. Inventory control in hybrid systems with remanufacturing [J]. Management Science,1999,45(5): 733-747.

[7] 肖迪,黄培清. 基于产品时间价值的闭环供应链库存策略研究[J]. 管理工程学报,2008,22(4): 146-148.

责任编辑：陆广品

Recycling and remanufacturing strategies of double-perishable products under the stochastic market demand

CAO Yu，ZHENG Qi-yun

(SchoolofBusiness,CentralSouthUniversity,Changsha410083,China)

closed-loop supply chain;double-perishable products;stochastic market demand;consumer recognition differences

Discussed the business operational decision of the double-perishable products in the stochastic market demand,which is based on the closed-loop supply chain as the research foundation,in considering both the recovery value of time variation and consumer acceptance of different circumstances. Conclusions: through the KKT condition given by nonlinear constrained optimization model and mathematical software,the optimal strategy of enterprise in various situations can be solved; in any case,the recovery is inversely proportional to the recycling of scale parameter ,but proportional to the remanufactured product cost saving; with the promotion of acceptance of remanufactured products,the profits of enterprise increase,the recovered strength enhances,but the optimal recovery time is postponed.

10.14182/j.cnki.j.anu.2016.06.012

2016-03-24；

2016-05-17

国家自然科学基金资助项目(71573281)；湖南省自然科学基金重点项目(12JJ2042)

曹裕(1985-)，女，湖南桃江人，副教授，博士生导师，研究方向为企业可持续运作管理、企业生命周期；郑其昀(1991-)，女，安徽宣城人，硕士研究生，研究方向为供应链可持续运作管理。

F224;274

A

1001-2435(2016)06-0743-07