依据断层摩擦准则估算的地壳主应力量值关系式及其参数分析

曹慧静　崔效锋　樊文杰

(中国地震局地壳应力研究所， 地壳动力学重点实验室， 北京　100085)



依据断层摩擦准则估算的地壳主应力量值关系式及其参数分析

曹慧静崔效锋*樊文杰

(中国地震局地壳应力研究所， 地壳动力学重点实验室， 北京100085)

基于Zoback(1992b)提出的估算地壳构造应力量值的思路和2个假设， 考虑了3个主应力分别为垂直主应力(对应3种构造应力类型)的情况， 比较系统地建立了依据应力形因子和断层摩擦强度估算构造主应力量值的关系式。讨论了摩擦系数、 孔隙压力系数和应力形因子对构造主应力量值的影响： 在最大主应力为近水平的情况下(应力类型为走滑型或逆断型)， 最大主应力量值(或随深度线性增加的斜率)随摩擦系数取值的增大而增大， 随孔隙压力系数取值的增大而减小。在最小主应力为近水平的情况下(应力类型为走滑型或正断型)， 最小主应力量值(或随深度线性增加的斜率)随摩擦系数取值的增大而减小， 随孔隙压力系数的增大而增大。并且， 3个参数对主应力量值估算的影响很大， 如果摩擦系数取值较大， 同时孔隙压力系数取值较小， 最大主应力随深度增加的斜率与最小主应力随深度增加的斜率之间的差异就大， 有可能导致不合理的结果出现。该方法只是对地壳岩石发生脆性破裂或摩擦滑动时的构造应力量值进行近似估算， 估算结果并不是地壳稳定状态下的构造应力量值。

应力量值摩擦系数孔隙压力应力形因子构造应力

0　引言

目前对地壳应力量值的研究较少， 尤其是地壳深部应力量值难以获取。 虽然原地应力测量可以直接获取浅层地壳应力状态， 得到地壳应力的大小和方向， 但由于技术难度大、 资金耗费高， 深部应力量值数据较少。有些学者尝试通过对浅层应力量值的回归分析推测地壳深部应力大小， 并且取得了一定的进展(王艳华等， 2012)。滑动方向拟合法的提出(Angelier， 1979； Gephartetal.， 1984； 许忠淮， 1985)， 使得人们不仅可以利用震源机制解、 断层擦痕、 跨断层形变观测等数据资料对地壳构造应力的方向进行反演计算， 而且可以得到反映主应力相对大小的应力形因子(谢富仁等， 1993， 2001； 崔效锋等， 2006； Hardebeck等， 2006； 张浪平等， 2014)。应力形因子为进一步研究分析应力量值提供了帮助。

Zoback(1992b)利用滑动拟合法给出的应力形因子， 提出了根据优势方位断层摩擦准则对地壳应力量值进行估算的思路， 该思路是估算分析地壳岩石发生脆性破裂或摩擦滑动时的构造应力量值的有效途径之一， 之后有学者采用该思路对多个地区的构造应力量值进行了估算分析(Plenefischetal.， 1997； 赵建涛等， 2002)。该思路需要借助岩石力学参数(摩擦系数、 孔隙压力)对构造应力量值进行估算； 因此， 科学合理地选取岩石力学参数就成为该方法中的1个重要问题。本文利用Zoback(1992b)提出的构造应力量值估算思路， 比较系统地建立了依据应力形因子和断层摩擦强度估算主应力量值的关系式； 在此基础上， 对影响主应力量值估算的岩石力学参数以及主应力量值估算关系式的适用性进行了初步讨论。

1　方法回顾

滑动方向拟合法是利用断面上的剪应力方向去拟合断面上的滑动方向， 从而获取平均偏应力张量的1种方法(Angelier， 1979； Gephartetal.， 1984； 许忠淮， 1985)。滑动方向拟合法在得到应力张量的3个主应力方向的同时， 还可以得到1个主应力量值之间比值的参数——应力形因子Φ：

(1)

式(1)中， σ1、 σ2、 σ3分别为最大主应力、 中间主应力和最小主应力。

增加2个约束条件， 就可以借助应力形因子Φ对3个主应力量值进行估算； 为此， Zoback提出了2个假设， 建立了2个约束条件(Zoback， 1992b)。2个假设为：

(1)若构造应力张量中有1个主应力方向近垂直， 则近垂直的主应力量值(用σv表示)近似于岩石静压力：

(2)

(2)地壳中最大应力差受优势方位断层摩擦强度所限(Byerlee， 1967； Jaegeretal.， 1979)：

(3)

式(2)、(3)中， ρ为岩石密度， g为重力加速度， μc为摩擦系数， h为地壳深度， P0为孔隙压力， σ1和σ3分别为最大主应力和最小主应力。

全球大陆多数地区的应力状态为走滑应力类型(Zoback， 1992a； 谢富仁等， 2003)。但也有一些地区存在不同的情况。以中国为例， 大量研究表明， 中国构造应力场在不同地区的应力作用方向和构造应力类型不同， 既有最大主应力为近水平的逆断应力类型和走滑应力类型， 也有最大主应力倾角很大的正断应力类型； 如山西地震带和鄂尔多斯周边地区多为正断应力类型， 而天山地区和龙门山地区则为逆断应力类型。因此根据不同的应力类型， 以不同的主应力作为垂直应力， 运用上述式(1)—(3)才可以对3个主应力量值进行合理的估算。

从式(1)—(3)还可以看出， 除垂直应力外， 摩擦系数、 孔隙压力等岩石力学参数的大小也对主应力量值的估算结果有很大的影响。 前人对这些岩石力学参数的影响没有做过细致分析， 只是根据相应的岩石力学参数研究结果， 选取一些特定的经验值或理论值对主应力量值进行估算； 如赵建涛等(2002)选取摩擦系数为0.85和0.6， 对唐山震源区的主应力量值进行了估算分析。本文对摩擦系数、 孔隙压力和应力形因子的取值大小对主应力量值的影响进行了初步分析。

2　主应力量值的估算关系式

上述估算方法的1个假设是构造应力张量中有1个主应力近垂直， 因此， 我们分别考虑3种构造应力类型： 1)走滑应力类型， 此时中间主应力σ2近垂直； 2)正断应力类型， 此时最大主应力σ1近垂直； 3)逆断应力类型， 此时最小主应力σ3近垂直。通过(1)—(3)3个等量关系式， 分别以σ1、 σ2或σ3代替σv， 即可得到估算3个主应力量值的关系式。

为了便于推导和分析， 令

(4)

则式(3)可表示为

(5)

式(4)、 (5)中A为与摩擦系数μc有关的参数， 并且A随着摩擦系数的增加而单调增加。

(1)应力类型为走滑型。此时σ2为垂直应力， 即σ2=σv； 其他2个主应力水平， 利用式(1)—(3)和式(5)可以推出计算式

(6)

(7)

(8)

对于孔隙压力， 可表示为1个比例系数乘以岩石静压力(陈颙等， 2009)：

(9)

本文称参数λ为孔隙压力系数。 一般来说，λ的取值范围为0～1， 其中几种特殊的情况为： 当λ=0时， 孔隙压力为零， 即相当于地壳岩石孔隙中无水干燥的情况； 当λ取0.4左右时， 孔隙压力近似为静水压力， 即地壳岩石中所有孔隙皆连通并且一直贯通至地面的情况。在不知道具体的孔隙压力时， 前人一般多用静水压力或相近值作为孔隙压力的近似值(Plenefischetal.， 1997； 赵建涛等， 2002)。当λ=1时， 孔隙压力等于岩石静压力， 因此在实际物理状态下，λ不可能为1。

将式(9)带入式(6)—(8)中， 则可以得到3个主应力量值随地壳深度变化的线性表达式：

(10)

(11)

(12)

从式(10)—(12)可以看出， 3个主应力量值随深度线性增加， 并受应力形因子、 摩擦系数和孔隙压力系数等3个参数的影响。另外， 当摩擦系数取值增大时，σ1值随之变大，σ3值随之变小； 当孔隙压力系数取值增大时，σ1值随之减小，σ3值随之变大； 当应力形因子取值增大时，σ1和σ3值随之变小。

(2)应力类型为正断型。此时σ1为垂直应力， 即σ1=σv； 其他2个主应力水平， 同样可以根据式(1)—(3)、 (5)、 (9)推出3个主应力量值随地壳深度变化的线性表达式：

(13)

(14)

(15)

从式(13)—(15)可以看出， σ2和σ3与摩擦系数呈反比关系， 当摩擦系数取值增大时， σ2和σ3值随之变小； σ2和σ3与孔隙压力系数呈正比关系， 当孔隙压力系数取值增大时， σ2和σ3值随之变大； 应力形因子只对σ2的变化有影响， 当应力形因子取值增大时， σ2值随之变大。

(3)应力类型为逆断型。此时σ3为垂直应力， 即σ3=σv； 其他2个主应力水平， 同样地根据式(1)—(3)、 (5)、 (9)不难推出3个主应力量值随地壳深度变化的线性表达式：

(16)

(17)

(18)

从式(16)—(18)可以看出， σ1和σ2与摩擦系数呈正比关系， 当摩擦系数取值增大时， σ1和σ2值随之变大； σ1和σ2与孔隙压力系数呈反比关系， 当孔隙压力系数取值增大时， σ1和σ2值随之减小； 应力形因子只对σ2的变化有影响， 当应力形因子取值增大时， σ2值随之变大。

虽然在式(1)—(3)中出现了3个参数， 即摩擦系数、 孔隙压力和应力形因子； 但当垂直应力为最大主应力或最小主应力时(即上文(2)和(3) 2种情况)， 最大主应力值和最小主应力值与应力形因子取值的大小无关， 中间主应力值随应力形因子取值的增大而增大。

3　讨论

3.1适用性讨论

本文基于Zoback(1992b)提出的估算地壳构造应力量值的思路， 推导了3种构造应力类型情况下的3个主应力量值随地壳深度变化的线性关系式。 该思路是建立在2个假设基础上的， 因此有必要对上述方法给出的应力量值做出说明。第1个假设是构造应力张量中的1个主应力接近垂直， 并用岩石静压力估算垂直主应力； 但实际情况中， 构造应力张量中的主应力方向并不完全是水平和垂直的(石耀霖， 2004)， 因此该方法只是对地壳构造应力量值进行估算， 并不能得到准确的地壳应力量值。第2个假设是地壳中的最大差应力受优势方位断层摩擦强度所限， 此时岩石为脆性， 因此该方法只是对地壳所能承受的最大应力量值进行估算。总的来说， 该方法只是对地壳岩石发生脆性破裂或摩擦滑动时的构造应力量值进行了近似估算， 估算结果并不是地壳稳定状态下的构造应力量值。

图1　岩石强度随应力变化示意图(据Kohlstedt et al.， 1995修改)Fig. 1　The change of rock strength with stress(adapted after Kohlstedt et al.， 1995).BDT为脆韧性转化处， BPT为脆塑性转化处

另外需要说明的是， 式(10)—(18)给出的3个主应力量值随地壳深度变化的线性表达式只对脆性的上地壳适用。地壳中影响岩石变形方式的因素有很多， 如围压、 温度、 孔隙压、 应变速率、 岩性、 结构等， 所以， 不同的学者对岩石变形的研究得到的结果不尽相同。在地壳中岩石干燥的情况下， 通常认为岩石脆韧性的转化发生在库伦准则和摩擦滑动曲线的相交处(Kohlstedtetal.， 1995； 图1)。由于随着地壳深度的增加， 温度和压力是上升的， 岩石状态会发生转化； 当地壳深部的岩石发生流动， 岩石发生明显的蠕变时， 地壳应力量值与蠕变速率及温度分布有关(Kohlstedtetal.， 1995； 图2)。结合图2 我们知道， 地壳中岩石脆性部分可能从地表延伸到十几千米深处， 在这部分脆性破裂区域， 才可以运用本文给出的关系式， 对地壳岩石脆性破裂或摩擦滑动时的构造应力量值进行近似的估算。

图2　大洋岩石圈和大陆岩石圈差应力随深度的变化图(据Kohlstedt et al.， 1995修改)Fig. 2　Change of differential stress with depth in oceanic lithosphere and continental lithosphere(adapted after Kohlstedt et al.， 1995).

3.2关于关系式中参数的讨论

由上节给出的关系式可以看出， 主应力量值随深度线性增加， 线性增加的斜率除了与岩石密度和重力加速度有关外， 还受摩擦系数、 孔隙压力系数和应力形因子取值的影响； 并且， 随着摩擦系数、 孔隙压力系数和应力形因子取值的不同， 主应力量值随深度线性增加的斜率存在着较大的变化。

3.2.1关于摩擦系数

在最大主应力σ1近水平的情况下(对应的应力类型为走滑型或逆断型)， 最大主应力量值(或随深度线性增加的斜率)随摩擦系数取值的增大而增大(式(10)、 (16))。在最小主应力σ3近水平的情况下(应力类型为走滑型或正断型)， 最小主应力量值(或随深度线性增加的斜率)随摩擦系数取值的增大而减小(式(12)、 (15))。当中间主应力σ2近水平时(应力类型为正断型或逆断型)， 摩擦系数对中间主应力量值的影响趋势与另一水平主应力相同(式(14)—(17))。

Byerlee(1978)在对岩石摩擦实验资料进行分析后提出， 当围压<200MPa时， 岩石的摩擦系数为0.85； 当围压≥200MPa时， 岩石的摩擦系数为0.6。近年来很多研究也发现， 某些地区断层或岩石的摩擦系数可能较低， 甚至可以低至0.1(Plenefischetal.， 1997； 单斌等， 2009； 何昌荣等， 2011)。如果摩擦系数可以在0.1～0.85范围内选取的话， 则最大主应力量值(或随深度线性增加的斜率)的变动范围就很大； 也就是说， 如果摩擦系数取值较大， 最大主应力量值(或随深度线性增加的斜率)就会很高。

为了清晰地展现摩擦系数对主应力量值估算的影响， 这里我们以走滑应力类型的关系式为例， 固定应力形因子和孔隙压力系数， 选取不同的摩擦系数估算主应力量值。图3 显示了当应力形因子和孔隙压力系数都取0.5， 摩擦系数分别取0.1、 0.4、 0.6和0.85时， 最大主应力和最小主应力量值的估算结果。 其中， 图3a清晰地展示了最大主应力量值与摩擦系数呈正比， 即当摩擦系数取值增大时， 最大主应力量值(随深度线性增加的斜率)随之变大； 图3b显示了最小主应力量值与摩擦系数呈反比， 即当摩擦系数取值增大时， 最小主应力量值(随深度线性增加的斜率)随之变小。

图3　摩擦系数对主应力量值估算结果的影响Fig. 3　The magnitude of principal stresses influenced by friction coefficient.a 最大主应力(σ1)量值估算结果； b 最小主应力(σ3)量值估算结果

3.2.2关于孔隙压力系数

孔隙压力系数对主应力量值的影响趋势与摩擦系数相反； 即在最大主应力σ1不是垂直应力的情况下(应力类型为走滑型或逆断型)， 最大主应力量值(或随深度线性增加的斜率)随孔隙压力系数取值的增大而减小(式(10)、 (16))。在最小主应力σ3不是垂直应力的情况下(应力类型为走滑型或正断型)， 最小主应力量值随孔隙压力系数的增大而增大(式(12)、 (15))。当中间主应力σ2为水平主应力时(应力类型为正断型或逆断型)， 孔隙压力系数对中间主应力量值的影响趋势与另一水平主应力相同(式(14)—(17))。

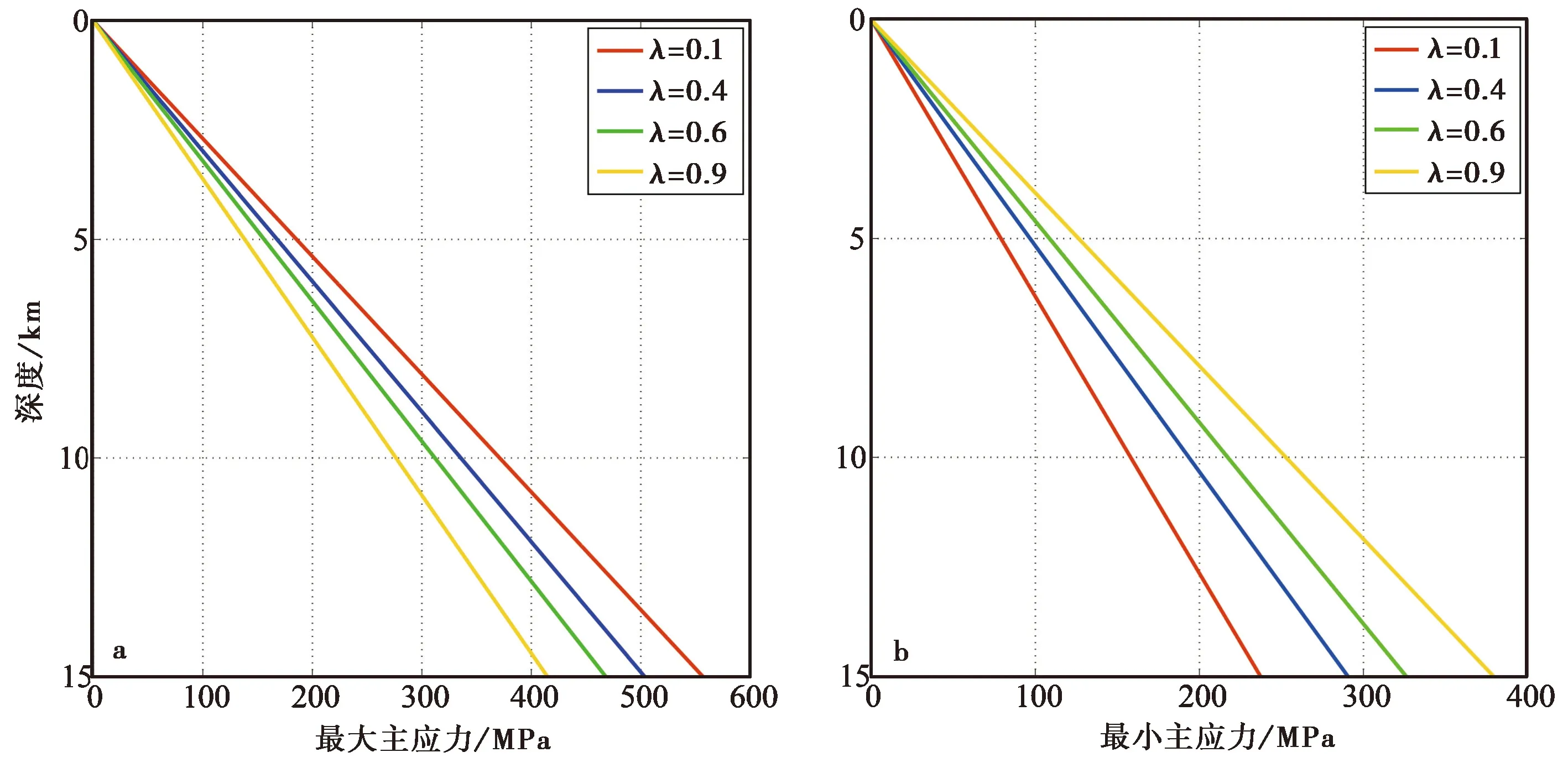
图4　孔隙压力系数对主应力量值估算结果的影响Fig. 4　The magnitude of principal stresses influenced by pore pressure.a 最大主应力(σ1)量值估算结果； b 最小主应力(σ3)量值估算结果

如前文所述， 如果孔隙压力系数可以在0≤λ<1范围内选取的话， 则最大主应力量值(或随深度线性增加的斜率)的变动范围就很大。 也就是说， 如果孔隙压力系数取值较大， 最大主应力量值(或随深度线性增加的斜率)就会小； 如果孔隙压力系数取值较小， 最大主应力量值(或随深度线性增加的斜率)就会很大。图4 显示了当应力形因子和摩擦系数都取0.5， 孔隙压力系数分别取0.1、 0.4、 0.6和0.9时， 运用走滑型关系式给出的最大主应力和最小主应力量值的估算结果， 直观地展现了最大主应力量值与孔隙压力系数呈反比(图4a)， 最小主应力量值与孔隙压力系数呈正比(图4b)。

3.2.3关于应力形因子

根据应力形因子的定义， 其取值范围也在0～1之间。 当应力形因子为0时， 中间主应力等于最小主应力； 当应力形因子为1时， 中间主应力等于最大主应力； 当应力形因子等于0.5时， 3个主应力量值呈等差排列。

图5　应力形因子对主应力量值估算结果的影响Fig. 5　The magnitude of principal stresses influenced by stress form factor.

除应力形因子等于0和1这2种特殊情形外， 对于正断和逆断应力类型来说， 中间主应力σ2近水平， 应力形因子只对中间主应力随深度线性增加的斜率有影响， 最大和最小主应力随深度线性增加的斜率与应力形因子无关。对于走滑应力类型， 中间主应力σ2近垂直， 其量值用岩石静压力来估算； 这时， 应力形因子直接影响到最大和最小主应力随深度线性增加的斜率。

同样， 我们以走滑应力类型的关系式为例， 取孔隙压力系数为0.4(约为静水压力)， 取摩擦系数为0.6， 应力形因子分别取为0、 0.2、 0.4、 0.6、 0.8和1， 对主应力量值进行估算(图5)。由图5 可以看出， 最大主应力量值和最小主应力量值与应力形因子呈反比， 随着应力形因子的增大， 最大主应力量值和最小主应力量值均减小。中间主应力为垂直压力， 用岩石静压力估算。

3.2.4参数对主应力量值的影响

摩擦系数和孔隙压力是地壳岩石力学参数， 由上述分析不难看出， 它们的取值大小直接影响到主应力量值的估算结果， 图3 —5 只展现了部分参数取值情况下的估算结果。如果摩擦系数取值较大， 同时孔隙压力系数取值较小， 最大主应力随深度增加斜率与最小主应力随深度增加斜率的差异就大， 在上地壳深部， 最大主应力与最小主应力的量值之差(即差应力)就会很大； 反之， 最大主应力与最小主应力的斜率和量值之差就会小些。例如， 当应力形因子取0.1， 摩擦系数取0.8， 孔隙压力系数取0.1时， 由式(10)估算的最大主应力量值在10km深处达800MPa， 此时， 最大主应力与最小主应力的量值之差达595MPa， 这显然偏高(参见3.1节)； 岩石在这么高的应力下已经转换为塑性(Kohlstedtetal.， 1995； Xuetal.， 2014)。

这一方面说明， 只有对1个地区的地壳岩石力学参数和应力形因子进行深入细致的研究， 获得比较可靠的摩擦系数、 孔隙压力和应力形因子等参数， 才有可能给出研究区比较可信合理的应力量值估算结果。另一方面也带给我们1个启示， 在不能很好地确定地壳岩石力学参数和应力形因子的情况下， 如果能够利用多学科的研究成果， 对摩擦系数、 孔隙压力和应力形因子等参数的取值范围进行限制， 就可以从宏观上对地壳岩石发生脆性破裂或摩擦滑动时的构造应力量值(即地壳能够承受的最大应力)范围进行估算， 进而借助多学科方法开展地壳应力积累变化研究， 以便获得对地壳构造应力量值更科学、 更合理的认识。

4　结论

(1)基于Zoback(1992b)提出的估算地壳构造应力量值的思路和2个假设， 考虑了3个主应力分别为垂直主应力(对应3种构造应力类型)的情况， 比较系统地建立了依据应力形因子和断层摩擦强度估算主应力量值的关系式。

(2)对影响主应力量值估算的3个参数(摩擦系数、 孔隙压力、 应力形因子)进行了初步分析。在最大主应力为近水平的情况下(对应的应力类型为走滑型或逆断型)， 最大主应力量值(或随深度线性增加的斜率)随摩擦系数取值的增大而增大， 随孔隙压力系数取值的增大而减小。在最小主应力为近水平的情况下(对应的应力类型为走滑型或正断型)， 最小主应力量值(或随深度线性增加的斜率)随摩擦系数取值的增大而减小， 随孔隙压力系数的增大而增大。当中间主应力为近水平时， 摩擦系数和孔隙压力系数对中间主应力量值的影响趋势与另1水平主应力相同。3个参数对主应力量值估算的影响很大， 如果摩擦系数取值较大， 同时孔隙压力系数取值较小， 最大主应力随深度增加斜率与最小主应力随深度增加斜率的差异就大， 有可能导致不合理的结果出现。

(3)本文给出的主应力量值随深度线性变化的估算关系式， 是建立在地壳中最大差应力受优势方位断层摩擦强度所限这一假设基础上的， 此时岩石为脆性； 因此， 该方法只是对地壳岩石发生脆性破裂或摩擦滑动时的构造应力量值进行近似估算， 估算结果并不是地壳稳定状态下的构造应力量值。

陈顒， 黄庭芳， 刘恩儒. 2001. 岩石物理学 [M]. 北京: 北京大学出版社.

CHEN Yong， HUANG Ting-fang， LIU En-ru. 2001. Rock Physics [M]. Peking University Press, Beijing(in Chinese).

崔效锋， 谢富仁， 张红艳. 2006. 川滇地区现代构造应力场分区及动力学意义 [J]. 地震学报， 28(5)： 451— 461.

CUI Xiao-feng， XIE Fu-ren， ZHANG Hong-yan. 2006. Recent tectonic stress field zoning in Sichuan-Yunnan region and its dynamic interest [J]. Acta Seismologica Sinica， 28(5)： 451— 461(in Chinese).

何昌荣， Verberne B A， Spiers C J. 2011. 龙门山断裂带沉积岩和天然断层泥的摩擦滑动性质与启示 [J]. 岩石力学与工程学报， 30(1)： 113—131.

HE Chang-rong， Verberne B A， Spiers C J. 2011. Frictional properties of sedimentary rocks and natural fault gouge from Longmenshan fault zone and their implications [J]. Chinese Journal of Rock Mechanics and Engineering， 30(1)： 113—131(in Chinese).

单斌， 熊熊， 郑勇， 等. 2009. 2008年5月12日MW7.9汶川地震导致的周边断层应力变化 [J]. 中国科学(D辑)， 39(5)： 537—545.

SHAN Bin， XIONG Xiong， ZHENG Yong，etal. 2009. Stress changes on major faults caused by MW7.9 Whenchuan earthquakes， May 12， 2008 [J]. Sci China (Ser D)， 39(5)： 537—545(in Chinese).

石耀霖. 2004. 地应力主应力的方位角求和与平均 [J]. 地震学报， 26(1)： 106—109.

SHI Yao-lin. 2004. Summation and decomposition of principal stresses in the crust [J]. Acta Seismologica Sinica， 26(1)： 106—109(in Chinese).

王艳华， 崔效锋， 胡幸平， 等. 2012. 基于原地应力测量数据的中国大陆地壳上部应力状态研究 [J]. 地球物理学报， 55(9)： 3016—3027.

WANG Yan-hua， CUI Xiao-feng， HU Xing-ping，etal. 2012. Study on the stress state in upper crust of China mainland based on in-situ stress measurements [J]. Chinese J Geophys， 55(9)： 3016—3027(in Chinese).

谢富仁， 崔效锋， 赵建涛. 2003. 全球应力场与构造分析 [J]. 地学前缘， 10(增刊)： 22—30.

XIE Fu-ren， CUI Xiao-feng， ZHAO Jian-tao. 2003. Analysis of global tectonic stress field [J]. Earth Science Frontiers， 10(Suppl)： 22—30(in Chinese).

谢富仁， 苏刚， 崔效锋， 等. 2001. 滇西南地区现代构造应力场分析 [J]. 地震学报， 23(1)： 17—23.

XIE Fu-ren， SU Gang， CUI Xiao-feng，etal. 2001. Modern tectonic stress field in southwestern Yunnan， China [J]. Acta Seismologica Sinica， 23(1)： 17—23(in Chinese).

谢富仁， 祝景忠， 粱海庆， 等. 1993. 中国西南地区现代构造应力场基本特征 [J]. 地震学报， 15(4)： 407— 417.

XIE Fu-ren， ZHU Jing-zhong， LIANG Hai-qing，etal. 1993. Modern tectonic stress field in southwestern China [J]. Acta Seismologica Sinica， 15(4)： 407— 417(in Chinese).

许忠淮. 1985. 用滑动方向拟合法反演唐山余震区的平均应力场 [J]. 地震学报， 7(4)： 349—361.

XU Zhong-huai. 1985. Mean stress filed in Tangshan aftershock area obtained from focal mechanism data by fitting slip directions [J]. Acta Seismologica Sinica， 7(4)： 349—361(in Chinese).

张浪平， 邵志刚， 李志海. 2014. 印度板块与欧亚板块在兴都库什—帕米尔地区相互俯冲的动力作用分析 [J]. 地球物理学报， 57(2)： 459— 471.

ZHANG Lang-ping， SHAO Zhi-gang， LI Zhi-hai. 2014. Dynamic action of mutual subduction between the Indian and the Eurasia plates in Hindu Kush-Pamir region [J]. Chinese J Geophys， 57(2)： 459— 471(in Chinese).

赵建涛， 崔效锋， 谢富仁. 2002. 唐山地震震源区构造应力场强度的初步分析 [J]. 地震学报， 24(3)： 268—276.

ZHAO Jian-tao， CUI Xiao-feng， XIE Fu-ren. 2002. Preliminary analysis of the tectonic stress intensity in the source region of Tangshan earthquake [J]. Acta Seismologica Sinica， 24(3)： 268—276(in Chinese).

Angelier J. 1979. Determination of the mean principal direction of stresses for a given fault population [J]. Tectonophysics， 56: 17—26.

Byerlee J D. 1967. Frictional characteristics of granite under high confining pressure [J]. J Geophys Res， 72: 3639—3648.

Byerlee J D. 1978. Friction of rocks [J]. Pure Appl Geophys， 116: 615— 626.

Gephart J W， Forsyth D W. 1984. An improved method for determining the regional stress tensor using earthquake focal mechanism data: Application to the San Fernando earthquake sequence [J]. J Geophys Res， 89: 9305—9320.

Hardebeck J L， Michael A J. 2006. Damped regional-scale stress inversions: Methodology and examples for southern California and the Coalinga aftershock sequence [J]. J Geophys Res， 111: B11310. doi: 10.1029/2005JB004144.

Jaeger J C， Cook N G W. 1979. Fundamentals of Rock Mechanics [M]. Chapman and Hall， London.

Xu Junshan， Wang Jianxin， Xu Congcong. 2014. The estimation of the maximum horizontal differential stress and its depth in the local lithosphere [C]∥Proceedings of the 48th US Rock Mechanics/Geomechanics Symposium， 2014， 2. 948—952.

Kohlstedt D L， Brian Evans， Mackwell S J. 1995. Strength of the lithosphere: Constraints imposed by laboratory experiments [J]. J Geophysics Res， 100(B9): 17587—17602.

Plenefisch T， Bonjer K P. 1997. The stress field in the Rhine Graben area inferred from earthquake focal mechanisms and estimation of frictional parameters [J]. Tectonophysics， 275: 71—97.

Zoback M L. 1992a. First and second order patterns of stress in the lithosphere: The world stress map project [J]. J Geophysics Res， 97(B8): 11703—11728.

Zoback M L. 1992b. Stress field constrains on intraplate seismicity in eastern North America [J]. J Geophysics Res， 97: 11761—11782.

Abstract

Based on Zoback’s method for estimating the tectonic stress magnitude and the two assumptions， we consider the conditions that three principal stresses are vertical principal stresses respectively(corresponding to three kinds of tectonic stress types). We deduced the formulae for estimating the tectonic stress magnitude by using the stress form factor and frictional strength of the fault and discussed the correlative influence of friction coefficient， pore pressure parameter and stress form factor on the stress value. When the maximum principal stress is approximately horizontal (when stress regime is strike-slip or reverse)， the maximum principal stress (or the slope of stress increasing linearly with depth) is positively related with the friction coefficient and negatively related with the pore pressure coefficient. When the minimum principal stress is approximately horizontal (when stress regime is strike-slip or normal)， the minimum principal stress (or the slope with depth) is negatively related to the friction coefficient， and positive to the pore pressure. Besides， these three parameters have great influence on the estimation of the tectonic stress magnitude. If the friction coefficient is too big and the pore pressure is too small， there could be a wide difference between the slope of the maximum principal stress increasing with depth and the slope of the minimum principal stress increasing with depth， which could lead to an unreasonable result. Our method is just an approximate estimation for the tectonic stress magnitude when crustal rocks have undergone brittle rupture or frictional sliding. The estimated results are not the tectonic stress magnitude when crust is in steady state.

ESTIMATING THE MAGNITUDE OF TECTONIC STRESS BASED ON THE FRICTION CRITERIA OF FAULT AND ANALYSING THE PARAMETERS’ INFLUENCE

CAO Hui-jingCUI Xiao-fengFAN Wen-jie

(KeyLabofCrustalDynamics，InstituteofCrustalDynamics，ChinaEarthquakeAdministration，Beijing100085，China)

stress magnitude， friction coefficient， pore pressure， stress form factor， tectonic stress

2015-05-26收稿， 2016-02-23改回。

国家科技支撑计划课题(2012BAK19B03)、 深部探测技术与实验研究专项(SinoProbe0604)和中央级公益性科研院所基本科研业务专项(ZDJ201414)共同资助。
*

崔效锋， 男， 研究员， E-mail: cuixfeng@sina.com。

P315.2

A

0253-4967(2016)02-386-11

曹慧静， 女， 1989年生， 硕士研究生， 主要从事地壳应力场研究， E-mail： doreen_jing@hotmail.com。

doi:10.3969/j.issn.0253- 4967.2016.02.012