移动床出口设置对卸料特性影响的离散模拟

肖　晓，苏景林，许光文，崔丽杰，刘晓星

（1中国科学院大学研究生院，北京 100049；2辽宁科技大学化学工程学院，辽宁 鞍山 114051；3中国科学院过程工程研究所，北京 100090）



移动床出口设置对卸料特性影响的离散模拟

肖晓1，苏景林2，许光文3，崔丽杰1，刘晓星3

（1中国科学院大学研究生院，北京 100049；2辽宁科技大学化学工程学院，辽宁 鞍山 114051；3中国科学院过程工程研究所，北京 100090）

采用离散单元法（DEM）模拟研究了二维移动床出口设置对物料卸料特性的影响。为验证模拟结果的合理性，首先针对单出口移动床进行了模拟研究，模拟结果表明：出口处颗粒质量流率满足修正的Beverloo经验关系式，而且定性上物料层内部流动区宽度随出口宽度的变化规律与实验结果吻合良好。在此基础上对两出口移动床的卸料特性进行了研究，得到以下结论：当出口宽度相等时，物料层内流动区宽度等于单出口条件下流动区宽度、出口间距及出口宽度的加和，而且每个出口处颗粒质量流率与单出口条件下颗粒质量流率相当；当出口宽度不相等时，增加大出口的宽度或减小出口之间的距离有助于提高小出口处颗粒质量流率，但大出口处颗粒质量流率基本保持恒定，不受小出口影响。

移动床；颗粒物料；多出口；离散单元法；数值模拟

DOI：10.11949/j.issn.0438-1157.20151714

引　言

作为一种常见的反应器及颗粒输运装置，移动床在化工领域得到广泛的应用。在自由流动条件下，依据其几何结构及内构件设置，移动床内颗粒物料可呈现整体流动（mass flow）或漏斗流（funnel flow）两种不同的流动结构［1］。当发生整体流动时，在垂直于流动方向的床层截面上颗粒速度近似相等，物料近似以活塞流的方式沿移动床轴向流动；在漏斗流情况下，沿垂直于颗粒流动的方向颗粒速度存在明显的梯度，颗粒的流动主要集中于出口的正上方，系统内形成流动区和静止/蠕动区。从力学角度，颗粒物料的整体流动可能会导致移动床侧壁受到的应力呈现剧烈的波动，进而有可能导致系统的坍塌，因此是不利的［2］；然而作为反应器或者输运装置，当移动床内颗粒物料形成漏斗流时颗粒在系统内的停留时间存在较宽的分布，而且系统内可能形成流动死区，这有可能导致相关流动、传递过程的异常。因此，在实际的工业应用中漏斗流流动结构通常是移动床设计优化中需要避免的［3］。

移动床内颗粒物料的流动形式与颗粒本身的属性及移动床本身的几何结构有关［4-7］。对于给定的颗粒物料及移动床，可通过添加内构件的方法促使颗粒物料形成整体流动［8-9］。对于底部宽度远大于出口宽度的移动床，促使颗粒物料整体流动的另一个有效方法是增加出口。如中国科学院过程工程研究所依托中国科学院战略先导科技专项“低阶煤清洁高效梯级利用关键技术与示范”正在研发的大型煤热解移动床反应器（底部宽度达5 m，出口宽度要求小于0.4 m），就是采用多出口的方式优化反应器内流料的流动特性。对于多出口移动床，为避免宽移动床内流动死区的形成，必须保证出口上方流动区之间发生重叠，进而确保宽移动床内颗粒物料形成整体流动。因此，深入认识多出口移动床中固体物料的流动特性对多出口移动床的出口设计和优化至关重要。

相比单出口移动床，多出口移动床中颗粒物料流动特性研究的文献报道相对较少，而且研究重点通常是多出口如何影响移动床卸料时的流动-堵塞转变［10-11］、颗粒混合［12-13］，对于移动床内颗粒物料流动特性则基本没有涉及。本工作采用离散单元法（discrete element method， DEM），对二维单出口和两出口移动床的卸料过程进行模拟研究，重点考察了移动床出口设置（出口个数、尺寸、出口间距）如何影响颗粒质量流率及床层内流动区宽度，为多出口移动床的出口设计和优化提供参考。

1　模拟及实验方法

离散单元法是目前国际上普遍采用的一种模拟离散颗粒物质的方法。其基本思想是将颗粒之间的碰撞接触作用抽象为弹簧、阻尼器及滑动摩擦器的共同作用［14］，进而基于Newton第二定律追踪每个颗粒的运动轨迹，最终得到整个颗粒系统的演化过程。

对于给定的颗粒i，其平动和转动遵循以下方程

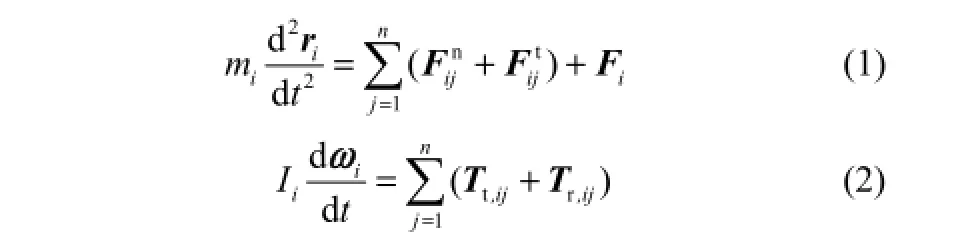
颗粒间的接触作用是离散单元法的核心。文献中关于颗粒碰撞时颗粒间作用力的本构方程有多种不同的表达形式。本工作采用的是最常用的一阶本构关系式，即作用力与颗粒之间的重叠量呈线性关系

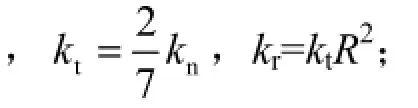
在DEM数值模拟中，颗粒被处理为可变性的软球，其变形程度由弹簧倔强系数控制。受计算能力限制，大规模模拟计算时弹簧倔强系数的取值一般会远小于真实值，即碰撞时颗粒间的重叠程度比真实值大。不同学者对离散单元法模拟中颗粒间重叠量的上限有不同的看法，从小于颗粒粒径的0.5%、1%到10%都有，取决于所研究的具体问题，以最大重叠量小于颗粒粒径的1%最为常见［15］。对最大颗粒重叠量的不同要求决定了模拟时间步长Δt的选择。

对于线性接触力模型，Hoomans提出了以下颗粒接触时间计算公式［16］

为了准确计算碰撞后颗粒的速度，一次碰撞事件的完成时间至少需要20～50个时间步长。在本工作中，基于式（6）得到时间步长，进而采用蛙跳算法对式（1）～式（5）进行离散求解。

为了制备处于紧密堆积、静止状态的颗粒物料，模拟中首先在移动床内部随机生成固体颗粒，并保证任何颗粒之间不存在几何接触。颗粒粒径均匀分布于（0.5，1）d之间。所生成的固体颗粒随后在重力作用下沉降，形成紧密堆积状态。已有的研究表明移动床的卸料特性与颗粒物料的初始堆积状态有关［4］。本部分工作重点是探讨移动床出口设置对卸料特性的影响。因此，为了最小化初始堆积状态对卸料特性的影响，在颗粒重力沉降过程中颗粒间摩擦系数统一设置为0。在开展卸料模拟时平动摩擦系数取所测得的实验用玻璃珠平动摩擦系数0.6。颗粒间转动摩擦系数很难通过物理实验准确测量，依据Tordesillas等［17］的研究，在本工作中转动摩擦系数设为0.2.

对于单出口移动床，初始物料堆积高度H=300d，共考察了5个不同的移动床宽度（W=200d～400d），以考察侧壁对颗粒物料流动特性的影响。对于两出口移动床，移动床宽度及初始物料堆积高度分别固定为400d和300d，此时颗粒总数约为200000个。为考察模拟结果的重复性，每个模拟条件都进行3次重复性模拟实验，下文所有数据都是3次模拟结果的平均值。事实上，由于重力沉降过程中摩擦系数设置为0且颗粒数量较大，重复性验证时不同算例结果间的差异很小，基本可以忽略。

为定性验证模拟结果的可靠性，本工作开展了实验室规模移动床卸料实验。实验材料为玻璃珠，其平均粒径d=1 mm。实验用移动床由透明有机玻璃板制成，宽度为400d，厚度为10d。移动床底部由两块可活动的透明有机玻璃板构成，实验中可通过调整有机玻璃板的相对位置控制移动床出口尺寸。玻璃珠的初始堆积高度约为300d。实验中，沿移动床轴向间隔布置透明和深蓝色玻璃珠，用CCD高速摄像仪记录整个卸料过程，考察物料的流动形态。

2　结果与讨论

2.1单出口条件

为验证模拟结果的可靠性，首先针对单出口移动床的卸料特性进行了模拟研究。图1给出了单出口条件下移动床内物料的流动特性。在出口尺寸显著小于移动床宽度的条件下，颗粒物料会呈现漏斗流流动结构，即颗粒流动主要发生于出口的正上方，出口两侧颗粒物料处于静止或蠕动状态，如图1（a）所示。流动区宽度与出口尺寸、物料堆积结构有关，而且是轴向高度的函数［4］。Babout等［4］定义了两种流动区宽度［图1（a）］：方法一是以物料层静止/蠕动区表面高度H为标准，取（1/2）H处的流动区宽度W（1/2）H；方法二是以物料层流动区表面最低点高度h为标准，取（1/2）h处的流动区宽度W（1/2）h。本工作参照Babout等的方法，在移动床物理实验的数据处理中以CCD拍摄图片的灰度对比确定流动区宽度；在DEM数值模拟中，由于颗粒速度是已知的，直接根据颗粒速度vy在x方向的分布［图1（b）］确定W（1/2）H和W（1/2）h。图1（c）给出了数值模拟得到的流动区宽度随时间的变化。与Babout等的实验结果一致，随着卸料的进行，流动区宽度逐步增大至一近似稳定值，而后逐渐减小。相比W（1/2）H，W（1/2）h的稳定区域更宽、更明显，因此在后文中以W（1/2）h为标准量化流动区的宽度。图1（d）给出了颗粒质量流率随时间的变化。与流动区宽度的变化趋势类似，颗粒质量流率首先迅速增大至一近似稳定值，随着卸料的进一步进行质量流率逐渐减小。后文中流动区宽度W（1/2）h和质量流率都是指稳定流动区间内时间平均的结果。

图1　单出口卸料不同物理量的变化Fig.1　Typical discharge dynamics（W=400d， H=300d， Woutlet=16d）

图2　流动区宽度与颗粒质量流率随移动床宽度的变化Fig.2　Variations of width of funnel zone and mass discharge rate versus width of moving bed

为检验模拟结果是否受移动床侧壁摩擦效应影响，模拟中考察了5种不同的移动床宽度，模拟结果如图2所示。图2表明，在本工作所考察的参数范围内，移动床边壁与出口之间的距离大于等于200d时即可保证W（1/2）h和出口质量流率Q（单位为g·s-1）与移动床侧壁近似无关。本工作中主要的模拟数据都是基于移动床宽度为400d情况下得到的，这确保了模拟结果不受移动床侧壁效应影响。

图3比较了流动区宽度W（1/2）h的数值模拟结果与实验结果。可以看到DEM数值模拟准确地复现了物理实验中观测到的W（1/2）h随出口宽度的变化趋势。数值模拟和物理实验结果都表明移动床出口存在一临界宽度：低于此临界值时，W（1/2）h随出口宽度的增大变化幅度较小；高于此临界值时，W（1/2）h随出口宽度的增大急剧增大。对于本工作中考察的移动床系统，该临界出口宽度约等于30d。图3也同时表明定量上数值模拟高估了流动区宽度，这主要是因为数值模拟中采用的是完全光滑、球形颗粒，而物理实验中所用的玻璃珠并不是完全球形且玻璃珠表面存在一定的粗糙度。此外，额外的辅助模拟结果表明流动区宽度W（1/2）h与颗粒的转动摩擦系数密切相关。然而，对于实际的颗粒准确测量其转动摩擦系数非常困难。本工作主要研究移动床出口对颗粒物料流动特性的影响，颗粒形状和物理力学属性的影响将在后续研究工作中详细考察。

图4给出了颗粒质量流率随出口宽度的变化。

Beverloo等［18］系统地研究了移动床卸料速率与出口尺寸之间的关系，并提出了以下经验关系式

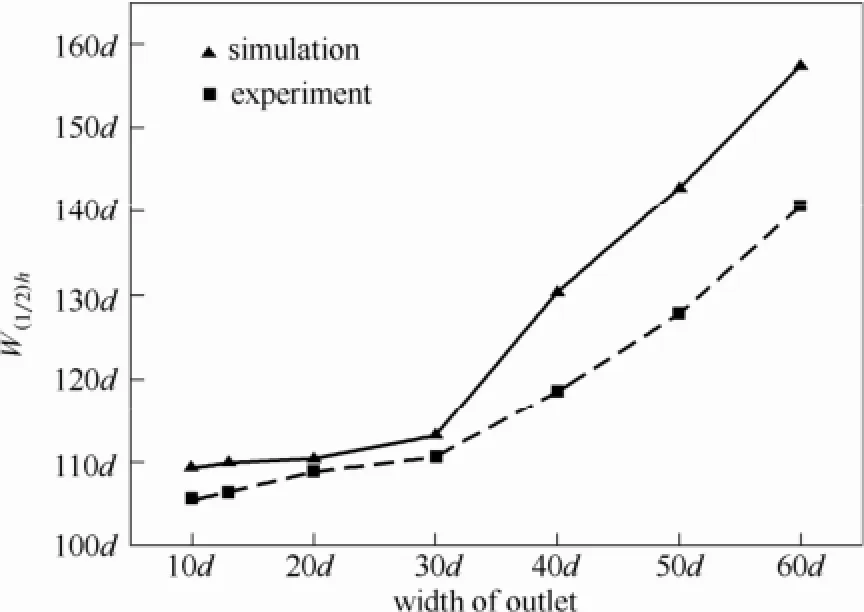
图3　流动区宽度随出口尺寸的变化Fig.3　Width of tube flow at different width of outlet

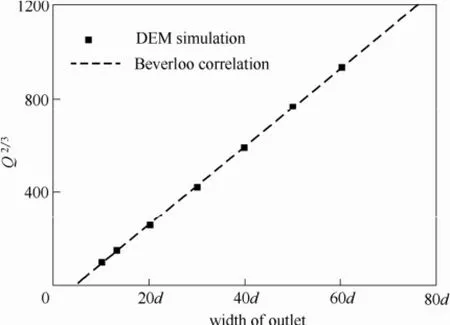
图4　颗粒质量流率随出口宽度的变化Fig.4　Variation of mass discharge rate with width of outlet

式中，Q为质量流率，kg·min-1；Wexit为出口宽度；k为Beverloo常数，其值在1～2之间。

对于方形出口（Loutlet×Woutlet）且Loutlet＞＞Woutlet条件下，研究表明Beverloo经验关系式应修正为［19］

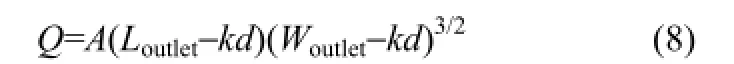
本工作是基于二维DEM模拟，因此按照式（8），模拟得到的颗粒质量流率与出口尺寸Woutlet应满足3/2次方关系。由图4可以看到Q2/3与出口尺寸间很好地满足线性关系，即模拟结果很好地吻合Beverloo经验关系式。

基于以上DEM数值模拟边界效应以及模拟结果合理性的验证，接下来对增加出口如何影响移动床卸料特性进行数值模拟研究。下文中如无特别说明，模拟中移动床宽度固定为400d，初始填料高度固定为300d。

2.2两出口条件

图5（a）给出了两出口时系统内颗粒物料的宏观流动结构。出口大小均为20d，出口间距为140d。可以看到增加出口后流动区宽度W（1/2）h显著增大，因此增加出口有利于提高颗粒物料在流动截面上的流动均匀性。图5（a）也表明，由于所考察的移动床底部是水平的，出口与出口之间形成了近似呈锥形的流动死区。图5（b）给出了两出口中部颗粒平均速度vy沿轴向的分布。可以看到存在一临界高度hs，低于此高度时颗粒的轴向流动速度近似为0，即颗粒不发生轴向流动。

图6给出了不同出口宽度Woutlet和出口间距Wo—o条件下hs的变化趋势。与单出口时W（1/2）h的变化趋势（图3）类似，hs随出口间距的变化趋势中出现一明显的拐点。在所考察的参数条件下，当出口间距小于100d时，hs随出口间距增大缓慢增大，但总体上hs的数值较小，即锥形流动死区范围较小，这主要是因为两个出口上方颗粒的快速流动使得出口间的颗粒物料受到强烈的剪切作用，促使颗粒物料发生流动；当出口间距大于100d时，锥形流动死区高度hs随出口间距增大快速增大。当出口间距等于180d时，hs近似等于物料层高度（图6中未给出），如图6（b）所示。在给定出口间距条件下，随出口宽度增大hs减小。对比图3可以看到，这主要是因为随出口宽度增大出口上方流动区宽度增大，因此相应地两个出口间的锥形流动死区范围变窄。

图7给出了不同出口尺寸和出口间距条件下W（1/2）h的变化趋势。图7（a）表明，与单出口条件类似，随着出口尺寸的增大，出口上方流动区宽度W（1/2）h单调增大；在给定出口尺寸的条件下，随着出口间距的增大，W（1/2）h单调增大。在本工作所考察的参数范围内，当出口间距小于等于140d时（1/2）h始终大于hs［图6（a）］，即在轴向位置1/2h处两出口间的固体物料总是发生轴向流动。图7（b）给出了扣除出口间距的影响后净流动区宽度 ［WD（h/2）=W（1/2）h-Wo—o-Woutlet］的变化趋势。图7（b）表明，净流动区宽度WD（h/2）近似为一恒定值，基本不随出口间距的变化而变化，而且与单出口时的W（1/2）h相当。这一结果说明，对于流动区宽度而言，出口之间的相互耦合效应基本可以忽略，多出口条件下固体物料流动区宽度近似等于单出口条件下流动区宽度乘以出口个数、出口间总间距两者的简单加和。

图5　等宽度两出口时典型流动结构及两出口中部颗粒轴向速度沿轴向的变化Fig.5　Typical discharge snapshot for bed with two same size outlets and variation of particle axial velocity along axialdirection

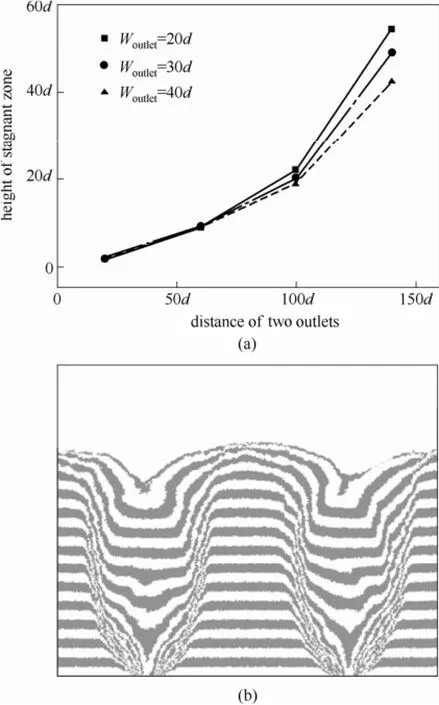
图6　静止区高度随两出口之间距离的变化Fig.6　Height of stagnant zone vs distance between two outlets

图7　流动区宽度随两出口之间距离的变化Fig.7　Width of flow zone vs distance of two outlets

图8给出了颗粒物料质量流量随出口间距的变化。与净流动区宽度WD（h/2）的变化趋势类似，颗粒质量流率基本不随出口间距变化，而且每个出口处的颗粒质量流率与单出口时颗粒质量流率近似相等，即在图8所考察的参数条件下两出口时每个出口处颗粒质量流率仍满足Beverloo经验关系式。

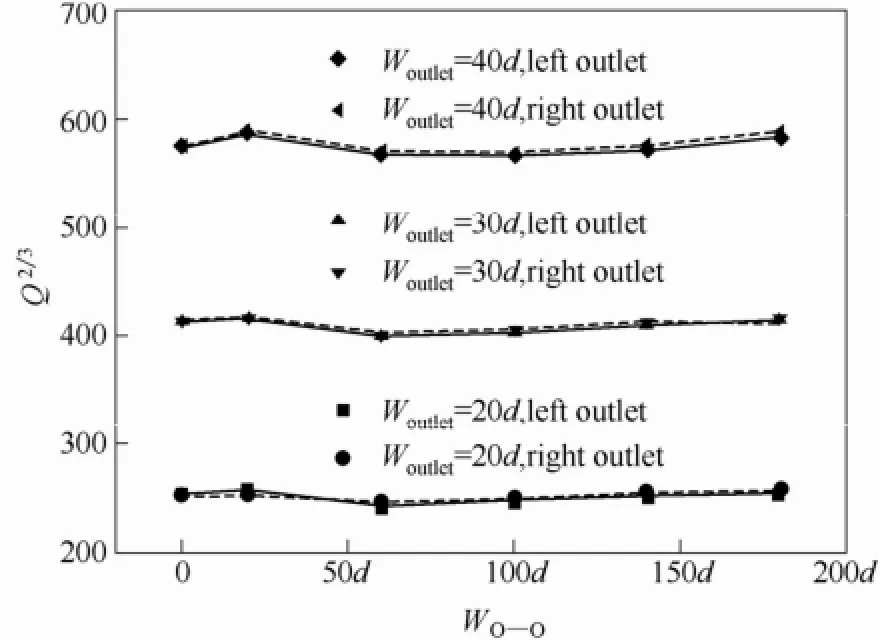
图8　两出口质量流量随两出口之间距离的变化Fig.8　Change of particle mass flux vs distance of two outlets

Kunte等［10］的研究结果表明，相比单出口移动床，两出口移动床的卸料特性存在明显的不同。在他们的移动床卸料DEM数值模拟中，移动床出口尺寸在3～4.4个颗粒粒径之间。在单出口条件下这一出口尺寸会导致卸料不连续，形成堵塞现象。Kunte等的数值模拟结果表明，适当地调整出口之间的距离会显著改善出口处的颗粒流动特性、降低堵塞概率，即出口间存在耦合效应。图8所考察的算例与Kunte等所考察的系统相比，最主要的区别在于移动床出口尺寸。在图8所考察的算例中，出口尺寸较大，系统始终保持连续稳定的颗粒流动。为全面了解两出口条件下出口间可能的耦合效应，本工作进一步考察了出口尺寸不相等条件下两出口移动床系统的卸料特性。

图9（a）给出了小出口宽度为10d时大出口宽度及出口间距对小出口处颗粒质量流率的影响。当出口间距为100d时，在所考察的大出口尺寸范围内（20d～60d），随着卸料的进行小出口处最终总会进入堵塞状态，即质量流率为0。这是因为小出口处形成了颗粒架拱，也就是散体力学领域所说的力链。孙其诚等［20］以及Peters等［21］的研究结果表明二维条件下力链长度在3～15个颗粒粒径范围内呈幂率形式单调衰减。这说明当移动床出口尺寸小于15个颗粒粒径时统计上系统总会出现堵塞状态。当两出口间距减小至60d时，小出口处可形成连续的颗粒流动；进一步减小出口间距会提高小出口处颗粒质量流率。定性上，这一结果与Kunte等的数值模拟结果相吻合，即减小出口间距有利于促进出口处颗粒物料的流动性，提高颗粒质量流率。造成这一现象的主要原因是颗粒物料的应力自活化效应［22］：局部的力学扰动有助于颗粒克服其周围颗粒对其的阻碍作用而发生运动。已有的研究结果表明［23］，当受到力学扰动作用时，密集颗粒物料的宏观有效摩擦系数会显著降低，即物料的流动性显著提高。在两出口条件下，大出口处物料的连续流动会导致局部应力波动。当该应力波动能有效传播到小出口上方时，由于应力自活化效应，小出口上方颗粒物料的流动性会显著提升。

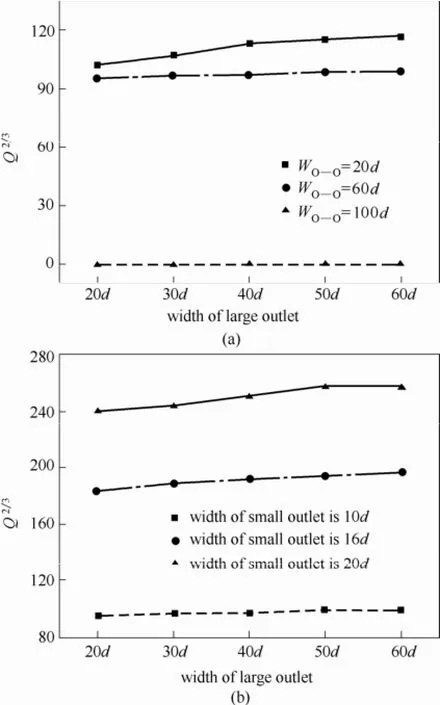
图9　小出口处颗粒质量流率随大出口宽度的变化Fig.9　Variation of mass discharge rate at small outlet with width of large outlet

图9（a）也表明，相比增加大出口宽度，减小出口间距更有助于提高小出口处颗粒质量流率。图9（b）给出了出口间距为60d时不同宽度小出口处颗粒质量流率随大出口宽度的变化。图9（b）表明，当小出口处形成稳定、持续颗粒流动后，尽管进一步增大大出口宽度有助于提高小出口处颗粒质量流率，但增幅不明显。这主要是因为局部应力波动在密集颗粒系统中的传播过程中会逐步衰减。Pouliquen等［22］认为，随着局部应力波动在系统中的传播，其强度随距离的-2次方幂律形式快速衰减。依据应力自活化效应模型，这说明相对大出口尺寸小出口处颗粒质量流率对出口间距更敏感。

图10　大出口处颗粒质量流率随大出口宽度的变化Fig.10　Variation of mass discharge rate at large outlet with width of large outlet

图10给出了图9模拟条件下对应的大出口处颗粒质量流率。与小出口处颗粒质量流率的变化规律不同，对于给定的大出口尺寸，该出口处颗粒质量流率基本保持恒定，而且其值与单出口时颗粒质量流率相当。

综合图8～图10可以看出，当出口尺寸存在差异时，小出口处颗粒质量流率与大出口尺寸、出口间距密切相关，而小出口处颗粒流动对大出口处颗粒质量流率的影响基本可以忽略。

3　结　论

以移动床卸料特性为研究对象，通过开展离散单元法（DEM）数值模拟研究了移动床内颗粒物料的流动特性，考察并分析了出口设置对系统内流动区宽度、出口处颗粒质量流率的影响，得出以下结论。

（1）二维移动床在单出口条件下颗粒质量流率满足修正的Beverloo经验关系式；存在一临界出口宽度，大于此数值时后床层内部流动区宽度随出口宽度增大而急剧增大，对于本工作中所考察的移动床系统该临界宽度约为30d。

（2）对于等宽度两出口移动床，每个出口处颗粒质量流率与等宽度单出口时颗粒质量流率近似相等，出口间不存在耦合效应；随着出口间距的增大，物料层内流动区宽度单调增大，但净流动区宽度（流动区宽度-出口间距-出口宽度）近似保持恒定，与出口间距近似无关，仅为出口宽度的函数；出口间流动死区的高度随出口间距增大而单调增大，存在一临界出口间距，大于此数值时流动死区高度随出口间距增大而迅速增大。

（3）两出口且出口宽度不相等的条件下，增加大出口宽度或降低出口间距有助于提升小出口上方颗粒物料的流动性，提高小出口处颗粒质量流率，但大出口处的颗粒质量流率近似保持恒定，不受小出口处颗粒流动影响。

References

［1］ SCHULZE D. Powders and Bulk Solids： Behavior， Characterization，Storage and Flow［M］. Heidelberg， Berlin： Springer， 2007.

［2］ WILDE K， TEJCHMAN J， RUCKA M， et al. Experimental and theoretical investigations of silo music ［J］. Powder Technology， 2010，198： 38-48. DOI： 10.1016/j.powtec.2009.10.012.

［3］ ZHU H P， ZHOU Z Y， YANG R Y， et al. Discrete particle simulation of particulate systems： a review of major applications and findings ［J］. Chemical Engineering Science， 2008， 63（23）： 5728-5770. DOI：10.1016/j.ces.2008.08.006.

［4］ BABOUT L， GRUDZIEN K， MAIRE E， et al. Influence of wall roughness and packing density on stagnant zone formation during funnel flow discharge from a silo： an X-ray imaging study ［J］. Chemical Engineering Science， 2013， 97： 210-224. DOI：10.1016/j.ces.2013.04.026.

［5］ HSIAU S S， SMID J， TSAI S A， et al. Flow of filter granules inmoving granular beds with louvers and sublouvers ［J］. Chemical Engineering and Processing， 2008， 47（12）： 2084-2097. DOI：10.1016/j.cep.2007.10.019.

［6］ 陶贺， 钟文琪， 金保昇， 等. 异径混合非球形颗粒在移动床中流动特性的数值模拟 ［J］. 东南大学学报（自然科学版）， 2012， 42（6）：1122-1126.DOI：10.3969/j.issn.1001-0505.2012.06.019. TAO H， ZHONG W Q， JIN B S， et al. Numerical simulation of flow characteristics of non-spherical particle mixture with different diameters flowing in moving bed ［J］. Journal of Southeast University（Natural Science Edition）， 2012， 42（6）： 1122-1126. DOI：10.3969/ j.issn. 1001-0505.2012.06.019.

［7］ 赵永志， 程易， 金涌. 颗粒移动床内不稳定运动的计算颗粒动力学模拟［J］. 化工学报， 2007， 58（9）： 2216-2224. ZHAO Y Z， CHENG Y， JIN Y. Computational granular dynamics simulation of unsteady movement in particle moving bed ［J］. Journal of Chemical Industry and Engineering（China）， 2007， 58（9）： 2216-2224.

［8］ HSIAU S S， SMID J， CHYOU Y P， et al. Impact of flow-corrective insert on flow patterns in two-dimensional moving bed ［J］. Chemical Engineering and Processing， 2013， 73： 7-15. DOI： 10.1016/j.cep. 2013.07.001.

［9］ ALONSO-MARROQUIN F， AZEEZULLAH S I， GALINDOTORRES， S A， et al. Bottlenecks in granular flow： when does an obstacle increase the flow rate in an hourglass ［J］. Physical Review E，2012， 85（2）： 020301（R）. DOI： 10.1103/PhysRevE.85. 020301.

［10］ KUNTE A， DOSHI P， ORPE A V. Spontaneous jamming and unjamming in a hopper with multiple exit orifices ［J］. Physical Review E， 2014， 90（2）： 020201. DOI： 10.1103/PhysRevE.90.020201.

［11］ MONDAL S， SHARMA M M. Role of flying buttresses in the jamming of granular matter through multiple rectangular outlets ［J］. Granular Matter， 2014， 16（1）： 125-132. DOI： 10.1007/s10035-013-0461-5.

［12］ CHENG Y M， CHAU K T， XIAO L J， et al.Flow pattern for a silo with two layers of materials with single or double openings ［J］. Journal of Geotechnical and Geoenvironmental Engineering， 2010，136： 1278-1286. DOI：10.1061/（ASCE）GT.1943-5606.0000334.

［13］ KAMATH S， KUNTE A， DOSHI P， et al. Flow of granular matter in a silo with multiple exit orifices： jamming to mixing ［J］. Physical Review E， 2014， 90（6）： 062206. DOI： 10.1103/PhysRevE.90.062206.

［14］ CUNDALL P A， STRACK O D L. A discrete numberical model for granular assemblies ［J］. Geotechnique， 1979， 29： 47-65.

［15］ Hoomans B P B. Granular dynamics of gas-solid two-phase flows［D］. Enschede， Nertherland： University of Twente， 1999.

［16］ YE M. Multi-level modeling of dense gas-solid two-phase flows［D］. Enschede， Nertherland： University of Twente， 2005.

［17］ TORDESILLAS A. Force chain buckling， unjamming transitions and shear banding in dense granular assemblies ［J］. Philosophical Magazine， 2007， 87（32）： 4987-5016. DOI： 10.1080/14786430701594848.

［18］ BEVERLOO W A， LENIGER H A. The flow of granular solids through orifices ［J］. Chemical Engineering Science， 1961， 15（3/4）：260-269.

［19］ MYERS M E， SELLERS M. Chemical Engineering， tripos part 2［R］. Cambridge： University of Cambridge， 1971.

［20］ 孙其诚， 金峰， 王光谦， 等. 二维颗粒体系单轴压缩形成的力链结构［J］. 物理学报， 2010， 59（1）： 30-37. SUN Q C，JIN F，WANG G Q， et al. Force chains in a uniaxially compressed static granular matter in 2D ［J］. Acta Phys. Sin.， 2010，59（1）： 30-37.

［21］ PETERS J F， MUTHUSWAMY M， WIBOWO J， et al. Characterization of force chains in granular material ［J］. Physical Review E， 2005， 72（4）： 041307.

［22］ POULIQUEN O， FORTERRE Y. A non-local rheology for dense granular flows ［J］. Philosophical Transactions of The Royal Society（A）， 2009， 367（1909）： 5091-5107. DOI：10.1098/rsta.2009.0171.

［23］ REDDY K A， FORTERRE Y， POULIQUEN O. Evidence of mechanically activated processes in slow granular flows ［J］. Physical Review Letters， 2011， 106（10）： 108301. DOI： 10.1103/PhysRevLett. 106.108301.

Discrete modeling of discharge dynamics of granular material in moving bed：effect of outlet setting

XIAO Xiao1， SU Jinglin2， XU Guangwen3， CUI Lijie1， LIU Xiaoxing3
（1University of Chinese Academy of Sciences， Beijing 100049， China；2Department of Chemical Engineering， University of Science and Technology Liaoning， Anshan 114051， Liaoning， China；3Institute of Process Engineering， Chinese Academy of Sciences，Beijing 100090， China）

The influence of outlet setting on the discharge dynamics of granular material in 2D moving beds was investigated by conducting discrete element simulations. To validate the simulation， a moving bed with single outlet was first modeled. The simulation results showed that the variation of discharge rate was tally with the modified Beverloo， and the variation tendency of the width of funnel zone was in agreement with the experimental data. Based on such validation， the discharge characteristics of granular material in the moving bed with two outlets were then systematically investigated. The simulation results indicated that as to the bed with two same size outlets， the width of funnel zone was simply equal to the sum of the width of funnel zone of the moving bed with one same size outlet， the distance between outlets and the width of outlet， and the granular mass discharge rate was roughly equivalent to that of the moving bed with one same size outlet. For the bed with two different size outlets， increasing the width of large outlet or decreasing the outlet distance was conducive to increasing thedischarge rate at small outlet. Nevertheless， the discharge rate at large outlet was not influenced by the small outlet and nearly kept constant.

date： 2015-11-13.

Prof. LIU Xiaoxing， xxliu@ipe.ac.cn； CUI Lijie， ljcui@gucas.ac.cn

supported by the National High Technology Research and Development Program of China （2013AA051204） and the Hundred Talents Program of Chinese Academy of Sciences.

moving bed； granular materials； multiple outlet； discrete element method； numerical simulation

TQ 018

A

0438—1157（2016）05—1710—09

2015-11-13收到初稿，2016-01-11收到修改稿。

联系人：刘晓星，崔丽杰。第一作者：肖晓 （1989—），女，硕士研究生。

国家高技术研究发展计划项目 （2013AA051204）；中国科学院“百人计划”项目。