基于遗传算法的焊装线工位平衡问题研究*

孟庆宇，李亮玉，龙　洋，岳建锋

(天津工业大学 天津市现代机电装备技术重点实验室， 天津 300387 )



基于遗传算法的焊装线工位平衡问题研究*

孟庆宇，李亮玉，龙洋，岳建锋

(天津工业大学 天津市现代机电装备技术重点实验室， 天津 300387 )

在现代化机器人焊装线生产过程中，大量的作业分配及多工位上焊接工序安排使焊接工位平衡问题表现的尤为突出。针对第二类平衡问题，即在给定工位数和各工序工时情况下，求解最优生产节拍问题进行研究。首先对该问题进行分析并建立节拍优化数学模型，进而提出了一种改进的遗传算法求解平衡问题。该算法以焊接工序的加工顺序优先关系作为约束条件，按种群个体适应度合理选择交叉概率和变异概率，提高算法搜索效率和解的可靠性。最后通过实例对该算法进行了验证。

焊装线；遗传算法；工位平衡

0　引言

机器人焊装生产线将多个焊接单元通过输送线和搬运机器人组合为整条生产线。在对机器人焊装线进行设计和规划时，通常做法是沿着焊装线依次排列各焊接工位，由焊接机器人单元在固定工位上精准、高效的完成焊接任务。焊接件的输送形式一般采用流水线，对各工位完工时间的同步性要求更高。这需要各工位间的生产节拍保持高度一致，否则会造成某些工位的任务过多无法按时完工，而另外工位由于任务少，已经完工等待上料。这种情况造成设备闲置而降低资源利用率，影响企业生产效率。焊装线工位间的焊接任务负荷不均会造成在制件积压，不但使当前工位任务无法按时完成，而且还会对后续生产环节造成很大影响，严重的甚至导致整线不能正常运行[1]。在现代化大规模、大批量生产条件下，需对多工位机器人焊装线上的大量焊接任务进行合理分配，这使得机器人焊装线平衡问题更显突出。

在生产平衡问题中，可将平衡问题按照不同的优化目标分为三类[2-4]：①生产节拍已知，求解最优工位数目；②工位数已知，求解最优生产节拍；③生产节拍和工位数已知，求最小平滑指数即负荷均衡指数。目前对于焊装线平衡问题的主要研究方法有[5-7]: ①目标规划法; ②启发式算法; ③人工智能算法。邓福平等采用自适应蚁群算法对装配线平衡问题进行求解[8]。张则强等提出带信息素总和规则的混合搜索机制的蚁群算法求解混流线平衡问题[9]。马亮采用遗传算法求解第一类平衡问题[10]，文章按照操作顺序优先关系为约束前提，将平衡问题简化为装箱问题并对其进行求解，得到最小工位数。但是该方法未考虑种群在不同进化时期的需求，未对交叉、变异概率进行调整。

本文对第二类平衡问题，以焊装线生产节拍为优化目标，提出在固定工位数目条件下求解机器人焊装线平衡问题。通过改进的遗传算法对焊装线上各焊接工位之间的作业工序的分配问题进行研究，在满足各工序优先顺序的条件下，实现所有工序的合理安排分配，优化焊装线生产节拍。最终实现各焊接工位作业负荷均衡，提高整线的平衡率。

1　焊装线平衡问题分类

焊装线平衡问题按照优化目标的不同可以划分为以下三类：

(1)已知生产节拍CT和各工序工时Ti，求最优工位数目m(SALBP-1)，其数学模型为：

(1)

maxη取最大值时，焊装线平衡率达到最优，此时求得最小工位数m。

(2)已知作业工位数m和各作业工序工时Ti，求最优生产节拍CT(SALBP-2)，其数学模型为：

(2)

在作业工位数m、各工位工时T(Sk)已知情况下，maxη表示焊装线平衡率达到最优，式中maxT(Sk)为所有工序中耗时最大工位工时，即瓶颈工位工时，此时生产节拍CT=maxT(Sk)。所以，在焊装线的平衡率达到最大时，将得到最优节拍CT。

(3)已知各工位生产节拍和作业工位数m，求最小平滑指数SI(SALBP-3)，其数学模型为：

(3)

minSI取最小值时表示整线负荷均衡指数最小，此时各工位工时T(Sk)最接近生产节拍CT。

2　焊装线平衡数学模型

对于第二类平衡问题，在满足各工序作业优先顺序约束条件下，将耗时较大的工位上的若干工序与耗时较短工位上的工序进行合理的调整。通过调整可以实现缩小生产节拍，使各工位的作业负荷达到最大均衡度，从而实现降低焊装线的平滑指数，提高焊装线平衡率，提高生产效率。

2.1数学模型假设

(1)焊装线上各工序的标准作业工时固定。

(2)各道工序为不可分最小单元且工序分配具有唯一性，即一道工序只能分配到一个工位。

(3)各道工序工时不大于其所在工位总工时。

(4)生产节拍不小于耗时最大工位的工时。

(5)焊装线各设备工作效率保持不变。

(6)焊装线上无并行工位。

2.2工序优先关系

采用遗传算法进行交叉、变异操作必须保证调整前后不改变各工序的优先作业顺序。对有n道工序的焊装线，各工序的优先顺序为n×n阶工序关联矩阵。矩阵元素为xij，工序间的优先关系约束表达为：

2.3优化方法

2.4优化目标模型

针对第二类平衡问题式(2)，在满足焊装线各道工序优先顺序的前提下，合理的调整和分配各工位的工序，可实现焊装线工位平衡率的提高，缩短生产节拍。

3　焊装线平衡遗传算法设计

本文采用改进的遗传算法对焊装线平衡问题进行求解。传统遗传算法有陷入局部最优解的缺点，并且交叉概率、变异概率固定，不能动态反映种群在不同进化时期的需求。对此，在保证种群多样性和优良基因不被破坏前提下，本文对不同进化时期的种群设计了交叉概率、变异概率与个体适应度之间的函数关系，提高算法的收敛效率，防止产生局部最优解。

3.1编码

首先对焊装线各道工序进行编码，得到所有工序的编码，然后在满足作业优先顺序的条件下，生成可行的染色体编码。图1为各道工序流程前驱图顺序及编号图。

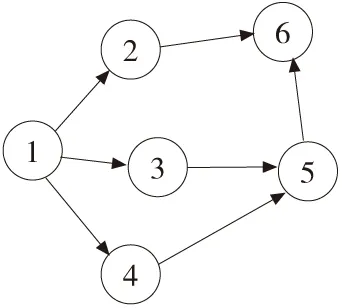
图1　工序流程前驱图及编号

如图1所示，将各道焊接工序[1 2 3 4 5 6]，按照其所示优先顺序分配到染色体基因位上，完成染色体编码。图2给出了两个染色体编码。

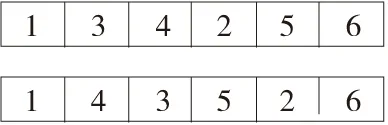
图2　染色体编码

通过该方法获得的染色体编码对操作算子和目标函数具有良好的适应性，减少算法计算量。

3.2染色体解码

染色体解码是将染色体中的编码转换为目标函数值的操作，种群中染色体编码表示可行的工序顺序，并未给出各道工序如何分配到不同工位，所以需要进行解码操作，明确各工序的焊接工位。具体操作为：

(2)按照初始节拍CT0，将焊装线现有的n道工序按照作业优先顺序分配到m个工位上，以T(Sk)(k=1,2,..m)表示各工位上工序工时总数，此时实际生产节拍:

CT′=maxT(Sk)k=1,2,3…m

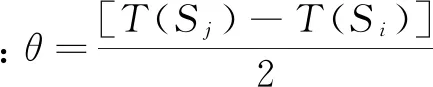
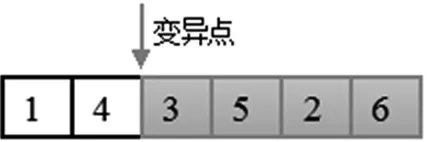
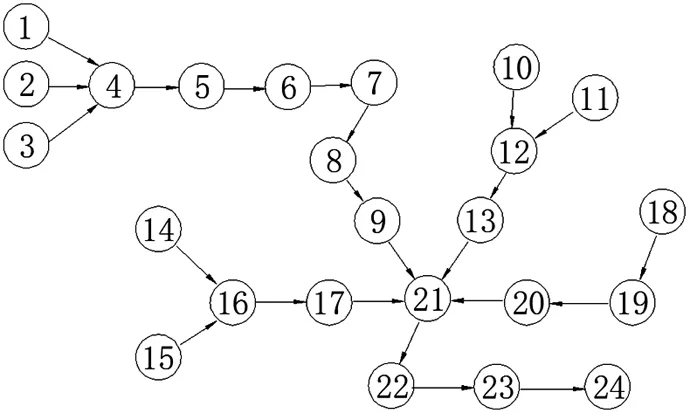
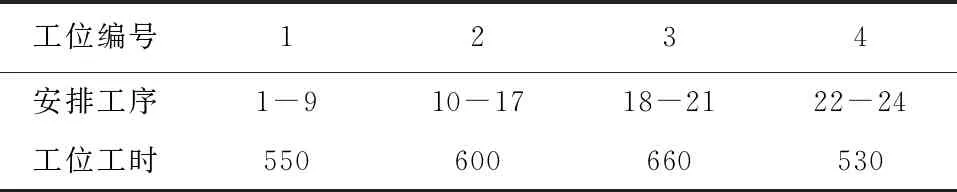
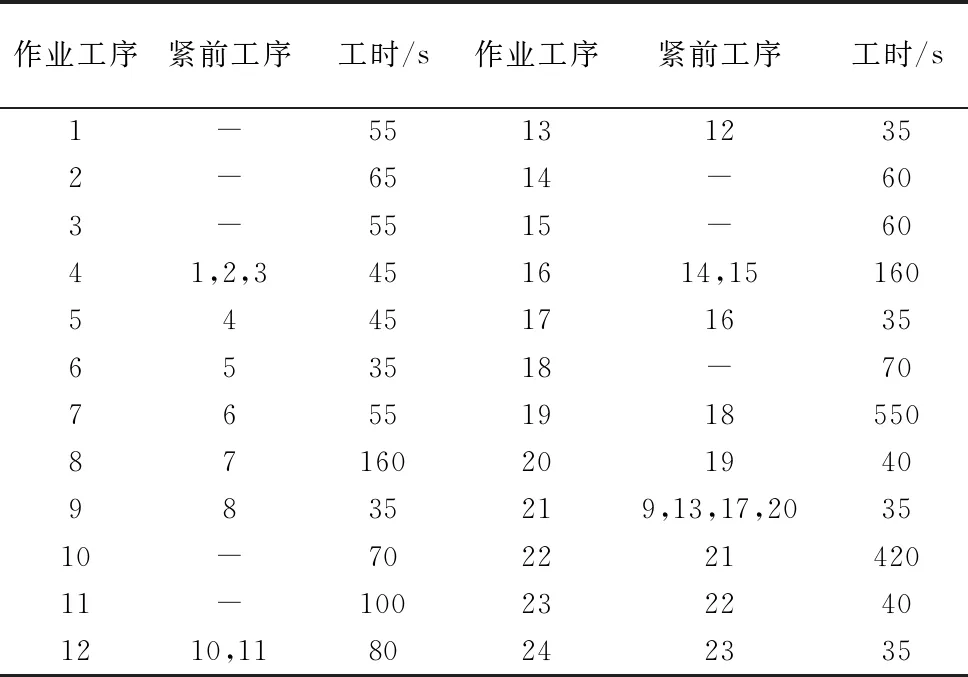
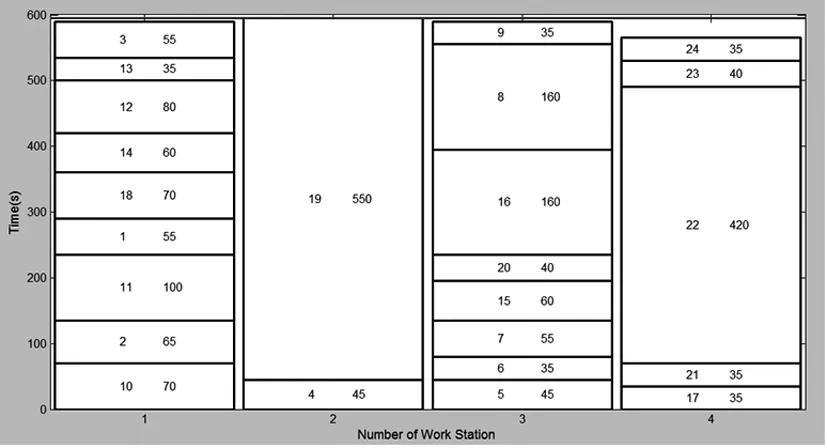
(4)根据θ值的大小按照已建立的数学模型中的优化方法对工位间的工序进行调整。设经过第一次调整后的节拍为CT1，若CT1

(5)更新调整后的生产节拍，重复步骤(3)、(4)，最终可求得趋于稳定的最优生产节拍。

3.3初始化

为防止遗传算法陷入局部最优，保证初始种群的多样性的同时使初始种群分散到解空间，本文采用随机选择方法进行种群初始化。

3.4适应度函数

适应度函数是衡量种群中个体性能的指标，是个体是否被选择复制到下一代的依据。通过适应度函数这一参数可以实现对种群结构的调整，保证群体中个体朝着优化的方向前进。本文根据焊装线生产节拍的目标函数，建立了如下图所示的适应度函数：

(5)

f函数是按照焊装线最优生产节拍建立的适应度函数，函数值越趋近于1表明各工位间综合工时差最小，生产节拍最优。

3.5选择操作

在种群进化到下一代过程中，必须保证种群染色体优良性，提高算法的运算性能。本文采取保优策略，使种群中具有较高适应度的优良个体更容易被选中，有更大的概率被选中进入下一代。本文根据个体适应度值设计了个体选择概率P:

(6)

式中，f(u)为个体u的适应度，f(v)为种群中任意个体的适应度，pop_size为种群个体数量。

3.6交叉操作

传统的遗传算法中按照固定的交叉概率对染色体是否进行交叉操作进行评价，这种固定参数不能及时的反应出种群在不同时期的进化需求，进而影响了算法的搜索效率和性能。在种群进化初期，个体适应度普遍不高，种群需要较大的交叉概率产生优良基因。种群进化后期，个体适应度普遍提高，为防止种群优良性被破坏，种群需要较小的交叉概率。为此，本文根据个体适应度设计了交叉概率函数：

(7)

本文交叉操作采用两点交叉方式，步骤如下：

(2)对各配对染色体进行交叉操作，随机生成[0,1]区间实数ω。若ω大于等于交叉概率Pc则进行交叉操作，否则该组染色体保持不变。

(3)在[1,N]区间随机生成两个整数作为两个交叉点，N为染色体长度(工序总数)，在交叉点之间进行染色体两点交叉操作。示例如图3所示。

图3　染色体交叉点

随机产生的交叉点为3、5，在染色体1中对应基因片段为[3、5、2]，该基因片段在染色体2中的可行顺序为[3、2、5]，将其替代染色体1中交叉点之间的基因片段得到交叉后的子代染色体，同理得到染色体2交叉操作后的子代染色体。父代染色体经交叉操作后的子代染色体如图4所示。

图4　交叉后的子代染色体

3.7变异操作

遗传算法中同样存在固定的变异概率不利于种群不同时期进化的现象。种群在不同的进化时期对变异概率有不同的需求。对此，本文考虑个体适应度因素设计了变异概率函数：

(8)

本文变异操作步骤如下：

(1)在[0,1]区间随机生成实数α，若α小于当前染色体变异概率Pm，则当前染色体保持不变，不执行变异操作。若α大于等于当前变异概率，则对当前染色体进行变异操作。

(2)对进行变异操作的染色体在[1,N-1]区间随机生成一个变异点，示例如图5所示。

图5　染色体变异点

(3)将变异点前的基因片段保留到子代染色体，变异点后的基因片段按照工序优先关联矩阵重新排列,经过重新组合获得变异后的染色体。对于上图示例染色体，基因片段[1、4]保持不变，将变异点后的基因片段[3、5、2、6]按照工序优先顺序进行重新排列为[2、3、5、6]，两段基因片段重新组合获得变异后的染色体，如图6所示。

图6　变异后的子代染色体

4　焊接工位平衡规划实例

为验证本文方法的可行性，以某壳体焊装生产线工位平衡规划问题为例，运用本文算法进行SALBP-2问题求解。

4.1壳体焊装线任务描述

该壳体机器人焊装线由4个焊接工位组成，各工位工时及工序如表1所示，各工序及优先作业顺序如图7工序前趋图所示。该焊装线共有24道生产工序，所有工序的标准作业工时及各工序的紧前工序如表2所示。

图7　焊装线工序前趋图

工位编号1234安排工序1-910-1718-2122-24工位工时550600660530

该焊装线调整前工位数m=4，各工位工时分别为550s、600s、660s、530s，此时生产节拍CT=660s。

表2　壳体焊装线作业工时及紧前工序

4.2平衡求解

基于MATLAB软件环境，在工位数为4时，通过对工序合理调整，提高焊装线平衡率，实现工位负荷均衡，求解最优生产节拍。结果如图8所示。

图8　m=4时焊装线平衡图

在上图中，横轴为工位，纵轴为各工位上工序工时总数，即各工位作业工时。由上可知，调整后各工位工时分别为：590s,595s,590s,565s，生产节拍和焊装线平衡率得到很大提高。

4.3结果对比

将本文算法得到的生产节拍CT、平衡率LE、平滑指数SI与原焊装线对比结果如表2所示。

表3 结果对比

经过调整，该壳体焊装线生产节拍缩短65s，平衡率提高9.7%，平滑指数减小59.46，该壳体焊装线的平衡率得到很大提高，工位间负荷均衡度得到很大改善，生产节拍得到有效提升。

5　结论

(1)本文对第二类平衡问题建立了以生产节拍为优化目标的焊装线平衡问题优化模型；并通过改进的遗传算法对该问题进行求解。

(2)该算法以工序间优先作业关系为约束随机生成初始种群，用本文提出的选择、交叉、变异方法，提高了种群搜索性能，提升种群个体多样性、优良性，有效的避免局部最优解产生。

(3)本文通过某壳体焊装线平衡问题实例求解，验证了模型和算法的可行性与有效性。前后结果对比表明算法能很好的解决焊装线平衡问题，提升了焊装线平衡率，降低了平滑指数，实现了生产节拍的优化。

[1] 唐秋华，席忠民，陈平和，等.混装线投产序列和工位任务的协同调度机理[J].工业工程,2008,11(1):19-24.

[2] 范维博,周俊,许正良.应用遗传算法求解第一类装配线平衡问题[J].计算机技术与发展,2010,20(2):194-196，201.

[3] 刘海江,汤伟,张含叶.基于改进粒子群算法求解第二类装配平衡问题[J].中国工程机械学报，2014,12(6):508-513.

[4] Arimin S,Christian B.Stata-of-the-art exacl and heuristic solution procedures for simple assembly line balancing[J].European Journal of Operational Research,2006,168(3):666-693.

[5] 卫东.给定序列的混合品种装配生产线平衡算法[J].机械工程学报,2004,40(4):135-138.

[6] 杨玉珍.基于元启发式算法的带生产约束作业车间调度问题若干研究[D].上海:华东理工大学，2014.

[7] 李尚健.应用改进的人工鱼群算法求解混合流水车间调度问题[D]．重庆:重庆大学，2013.

[8] 邓福平.基于蚁群算法的装配线平衡问题研究[D]．武汉:华中科技大学，2014.

[9] 张则强，程文明，钟斌，等.混合品种装配线平衡问题的一种混合搜索机制的蚁群算法[J].机械工程学报，2009,45(5):95-101.

[10] 马亮，张广明.基于遗传算法的焊接生产线工位平衡规划算法[J].自动化应用,2011(8):9-13.

(编辑李秀敏)

Research of Work-station Balancing Problem of Welding Line Based on the Genetic Algorithm

MENG Qing-yu,LI Liang-yu,LONG Yang,YUE Jian-feng

(Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology，Tianjin Polytechnic University， Tianjin 300387，China)

In the prodution process of modern robot welding line,the reasonable arrangement of lots of task allocation and the welding process of work-stations makes the problem of welding station balancing more important.According to the second category of balancing problem,namely finding the best takt time under the condition of a given work-stat number and working hours in each process,firstly analyze the problem and establish the mathematical modle,then puts forward an improved genetic algorithm to solve the balancing problem.This paper uses the priorities of all the welding processes order as constraint conditions,the cross probability and mutation probability are selected according to the population individual fitness rational,improved the searching efficiency of algorthm and the reliability of the solution.Finally the algorithm is verified by an example.

welding line;the genetic algorithm;work-station balance

1001-2265(2016)07-0127-04DOI:10.13462/j.cnki.mmtamt.2016.07.036

2015-09-08

国家自然科学基金资助项目(U1333128)；天津市科技计划项目(14ZCDZGX00802)；天津市科技特派员项目(15JCTPJC58400)

孟庆宇(1988—)，男，河北衡水人，天津工业大学硕士研究生，研究方向为机器人焊装线控制方法及节拍优化,(E-mail)mqy2007@163.com。

TH136;TG506

A