圆锥计算题，“展开”来思考

杭寿华



圆锥计算题，“展开”来思考

杭寿华

圆锥计算问题一直是每份中考试卷中都要出现的，而且大多出现在每种题型的较偏后的位置，也就是说还有一定的难度.那么这类问题如何不丢分呢？试举几例，帮助同学们“展开”思考.

例1（2015·徐州）用一个圆心角为90°，半径为4的扇形围成一个圆锥的侧面，该圆锥底面圆的半径为_______.

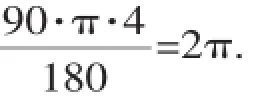
∵圆锥的底面圆周长等于它的侧面展开图的弧长，∴根据圆的周长公式，得2πr= 2π，解得r=1.

【反思回顾】可以发现，将圆锥的侧面展开图与底面圆周长对应起来是解题的关键.

例2（2015·扬州）已知一个圆锥的侧面积是2π cm2，它的侧面展开图是一个半圆，则这个圆锥的高为_______cm（结果保留根号）.

【思路讲解】如图1，

∵圆锥的侧面积是2π cm2，它的侧面展开图是一个半圆，

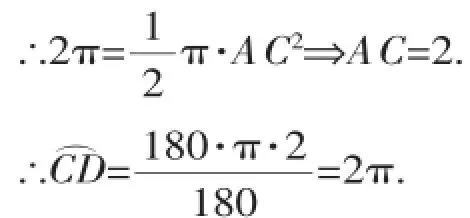
∵圆锥的底面圆周长等于它的侧面展开图的弧长，∴根据圆的周长公式，得2π·BC= 2π⇒BC=1.

在Rt△ABC中，由勾股定理，得

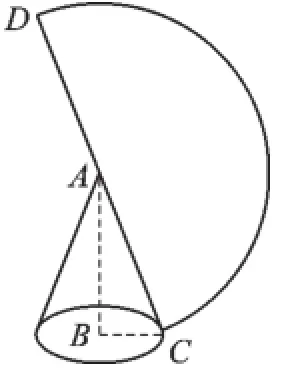
图1

【反思回顾】绘出草图，寻找展开扇形与底面圆之间的对应关系有助于思考，建议同学们学习这样的数形结合的解题习惯和方法.

小试身手

1.（2015·连云港）如图2是一个几何体的三视图，其中主视图与左视图都是边长为4的等边三角形，则这个几何体的侧面展开图的面积为_______.

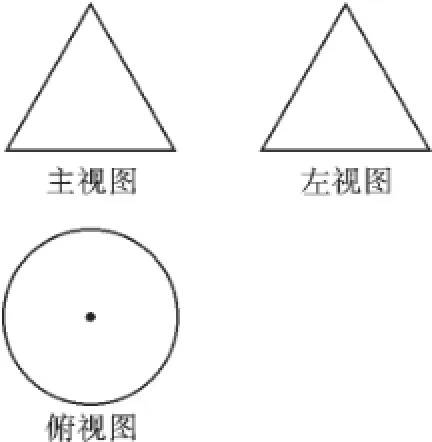
图2

2.（2015·常州）已知扇形的圆心角为120°，弧长为6π，则扇形的面积是_______.

参考答案

1.∵由三视图可知这个几何体为圆锥，圆锥的母线长为4，底面圆的直径为4，

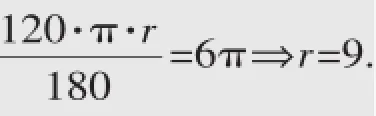
（作者单位：江苏省南通市新桥中学）