洞察结构：“中点四边形”变着花样考

王芳



洞察结构：“中点四边形”变着花样考

王芳

在四边形解题过程中，同学们一定对“中点四边形”有着深刻的印象，它的确是中考试卷中的宠儿，熟悉它的结构和常见变式对于迅速贯通解题思路有着非常重要的作用.下面选两道考题，与同学们一起思考.

例1（2015·无锡）如图1，已知矩形ABCD的对角线长为8 cm，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的周长等于_______cm.

图1

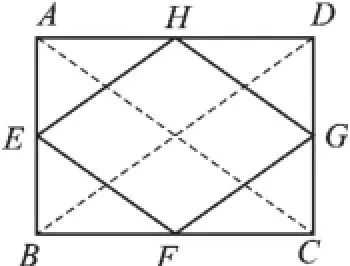
图2

【思路讲解】一般思路是连接AC、BD，如图2，

∵四边形ABCD是矩形，

∴AC=BD=8（cm），

∵E、F、G、H分别是AB、BC、CD、DA的中点，

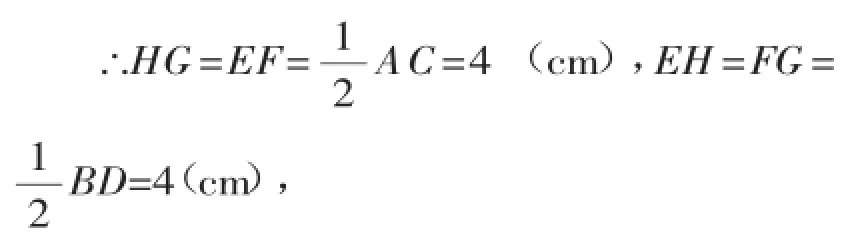
∴四边形EFGH的周长等于4+4+4+4= 16（cm）.

然而，根据我们的教学经验，常常发现不少优秀学生只要3秒就能搞定这样的考题.他们第1秒首先识别确认这是矩形的中点四边形问题，则该中点四边形EFGH是菱形；第2秒连接对角线AC，BD，确认AC= BD=8 cm；第3秒则利用三角形中位线性质得出EF=4 cm，从而得出菱形EFGH周长为16 cm.

【回顾反思】上面我们讲解的“优秀学生的思路”你理解吗？你是否用的是这样的方法呢？事实上，对于惜时如金的考场，谁在这些基础题、熟悉题的解题速度上胜出，谁就赢得了更多的时间去突破攻克把关题.

例2（2015·南京）如图3，AB∥CD，点E，F分别在AB，CD上，连接EF，∠AEF、∠CFE的平分线交于点G，∠BEF、∠DFE的平分线交于点H.

（1）求证：四边形EGFH是矩形；

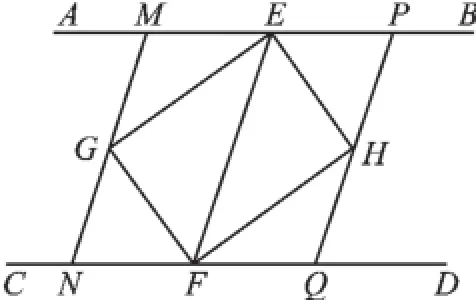
图3

（2）小明在完成（1）的证明后继续进行了探索，过G作MN∥EF，分别交AB，CD于点M，N，过H作PQ∥EF，分别交AB，CD于点P，Q，得到四边形MNQP，此时，他猜想四边形MNQP是菱形，请在下列框中补全他的证明思路.

由AB∥CD，MN∥EF，PQ∥EF，易证四边形MNQP是平行四边形，要证平行四边形MNQP是菱形，只要证MN=NQ，由已知条件______________，MN∥EF，故只要证GM=FQ，即证△MGE≌△QFH，易证____________ ________，_________________，故只要证∠MGE=∠QFH，易证∠MGE=∠GEF，∠QFH=∠EFH，_______________，即可得证.

【思路讲解】

（1）利用角平分线的定义结合平行线的性质得出∠FEH+∠EFH=90°，进而得出∠GEH=90°，进而求出四边形EGFH是矩形；

（2）利用菱形的判定方法首先得出要证▱MNQP是菱形，只要证MN=NQ，再证∠MGE=∠QFH得出即可.

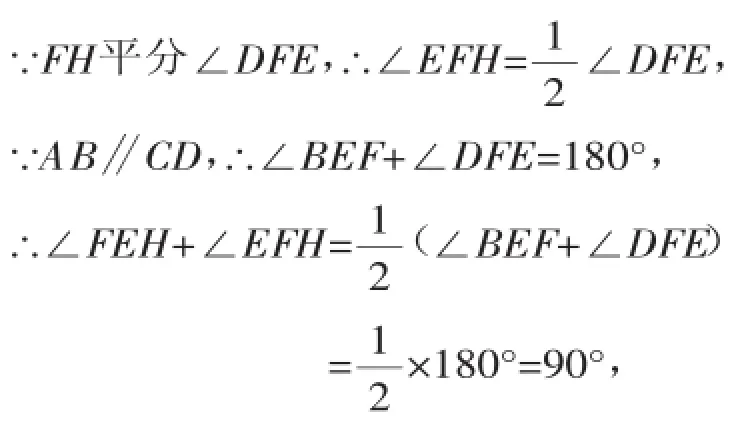
∵∠FEH+∠EFH+∠EHF=180°，

∴∠EHF=180°-（∠FEH+∠EFH）

=180°-90°=90°，

同理可得：∠EGF=90°.∵EG平分∠AEF，∵EH平分∠BEF，

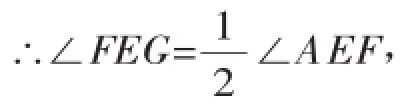
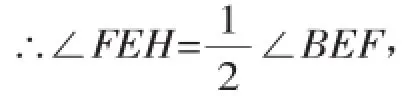
∵点A、E、B在同一条直线上，

∴∠AEB=180°，即∠AEF+∠BEF=180°，

∴四边形EGFH是矩形.

（2）解：答案不唯一：

由AB∥CD，MN∥EF，PQ∥EF，易证四边形MNQP是平行四边形，

要证▱MNQP是菱形，只要证MN=NQ，由已知条件：FG平分∠CFE，MN∥EF，

故只要证GM=FQ，即证△MGE≌△QFH，易证GE=FH，∠GME=∠FQH.

故只要证∠MGE=∠QFH，易证∠MGE= ∠GEF，∠QFH=∠EFH，∠GEF=∠EFH，即可得证.

【反思回顾】事实上，这道考题是把同学们熟悉的中点四边形改编呈现，原命题如果看作：菱形MNQP的中点四边形EGFH是矩形，这道考题的本质就是要求同学们回答：中点四边形EGFH是矩形时，原四边形（易证平行四边形）是菱形.搞清问题的本质后，我们也可提出如下问题，供同学们继续思考：

（3）连接MQ，NP，求证：MQ、NP互相垂直平分；

（4）连接MQ，设MQ交EF于O，O是否为矩形EGFH的对称中心？为什么？

（作者单位：江苏省海安县城南实验中学）