热点聚焦：特殊四边形与图形变换考题

2016-08-20严冬梅

初中生世界 2016年23期

关键词：辅助线过点考题

严冬梅

热点聚焦：特殊四边形与图形变换考题

严冬梅

【编者按】本篇之前，我们已刊发一篇平行四边形与翻折的辅导文章，然而初中阶段的另外两种变换，即平移、旋转，也常常以特殊四边形为载体设计考题，这里我们再选用一篇文章介绍特殊四边形与平移、旋转变换相结合的考题，希望启发同学们对这类考题的思考.

初中阶段主要学习了三种图形变换（平移、翻折、旋转），这三种变形在中考卷中都会考查，而且常常与特殊四边形结合在一起进行考查.下面围绕特殊四边形与平移、旋转两种变换的综合考查做些辅导讲解.

例1（2015·镇江）如图1，△ABC和△DBC是两个具有公共边的全等三角形，AB=AC=3 cm，BC=2 cm，将△DBC沿射线BC平移一定的距离得到△D1B1C1，连接AC1，BD1.如果四边形ABD1C1是矩形，那么平移的距离为_______cm.

图1

【思路讲解】如图2，过点A作AE⊥BC于点E，

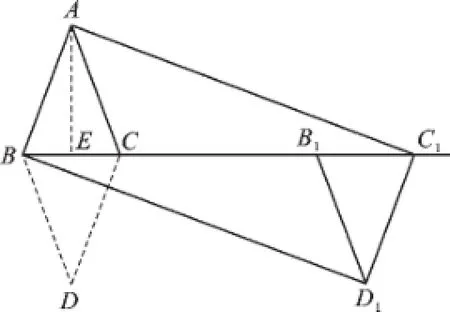
图2

∵∠AEB=∠AEC1=90°，

∴∠BAE+∠ABC=90°.

∵四边形ABD1C1是矩形，∴∠BAC1=90°，∴∠ABC+∠AC1B=90°，

∴∠BAE=∠AC1B，

∴CC1=BC1-BC=9-2=7，即平移的距离为7 cm.

【反思回顾】从上面的思路来看，破题的关键点至少有三处：第一利用等腰三角形三线合一性质作出辅助线；第二，在草稿本上画出相对精准平移后的图形；第三，利用所得矩形的性质捕捉和利用相似三角形性质解题.当然，在图2中，“△ABE∽△C1BA”是经典的“射影定理”基本图形，同学们应该积累这样的常见模式，看到这种图形，还应该很快得出“比例中项”的式子：AB2=BE· BC1.熟悉这些模式，对于提高填空、选择题的解题效率无疑是很有作用的.

例2（2015·连云港，有删减）在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD与边长为2的正方形AEFG按图3位置放置，AD与AE在同一直线上，AB与AG在同一直线上.

（1）小明发现DG⊥BE，请你帮他说明理由.

基于数据挖掘探讨含“桔梗-甘草”药对成方制剂的证治规律…………………………………………………… 吕建军等（20）：2813

（2）如图4，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长.

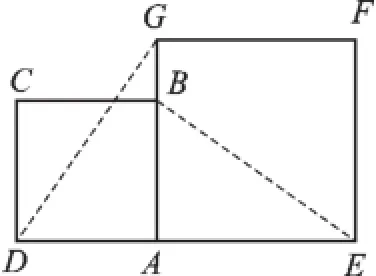
图3

图4

【思路讲解】

（1）由四边形ABCD与四边形AEFG为正方形，利用正方形的性质得到△ADG和△ABE的两对边相等，且夹角相等，利用SAS得到△ADG≌△ABE，利用全等三角形对应角相等得∠AGD=∠AEB，作辅助线“延长EB交DG于点H”，利用等角的余角相等得到∠DHE=90°，再由垂直的定义即可得DG⊥BE.

（2）由四边形ABCD与四边形AEFG为正方形，利用正方形的性质得到△ADG和△ABE两对边相等，且夹角相等，利用SAS得到△ADG≌△ABE，利用全等三角形对应边相等得到DG=BE，作辅助线“过点A作AM⊥DG 交DG于点M”，则∠AMD=∠AMG=90°，在Rt △AMD中，根据等腰直角三角形的性质求出AM的长，即为DM的长，根据勾股定理求出GM的长，进而确定出DG的长，即为BE的长.

【规范解答】

（1）∵四边形ABCD和四边形AEFG都为正方形，∴AD=AB，∠DAG=∠BAE=90°，AG=AE，

∴△ADG≌△ABE（SAS），

∴∠AGD=∠AEB.