放大“思考题”思考的价值

○蒋守成

放大“思考题”思考的价值

○蒋守成

●思考题的教学需要我们站在儿童的思维和生活经验的角度去创新，鼓励学生刨根问底、追根溯源，引导学生用自己喜欢的方式去思考，真正享受到高品质的数学学习生活。

推动学生思维发展是数学教学的本质。我们要在数学课堂上不断制造让学生去“想”的事件，引导学生运用数学的思维方式进行思考，拓展思维的广度和深度，提升数学思维品质。思考题的教学就是培养学生思维能力的很好的载体。

如何通过思考题的教学来引导学生更广泛地了解数学知识，积累数学活动经验，感悟基本的数学思想，放大其思考的价值呢？这需要我们系统研读“思考题”栏目，深入解读编写意图，依据学生的年龄特点和认知水平，充分挖掘教学资源，一方面和课堂教学有机整合，达成拓展提升的目标，另一方面开发思考题专题课，从“一个”思考题中拓展，从“多个”相近的思考题中聚合，从“全册”思考题中知新，达成全面提升学生思维水平的目标。

一、融合日常课堂教学，凸显“思考题”的思考价值

小学数学学习的现实意义不仅仅是套用某些公式去解决一些模仿性的问题，其更重要的意义在于培养从现象中抽取本质、从大量信息中发现内在的规律、从繁杂中寻求简洁等数学思维能力。因此，我们力求对每一道思考题的教学功能都清晰明了，进行教学化加工，化深奥为浅显，并和教学内容相融合成为日常课堂教学的一部分，帮助学生养成发现问题、提出问题的能力，逐步体悟到蕴涵其中的数学思想方法。

1.和新授课相融合，给学生制造“想”的事件。

教材内容是按知识的逻辑顺序和学生的身心发展规律来编排的，侧重于链状排列，系统性、理论性较强。思考题与必学内容有机联系相互补充，既能使学生系统地学“深”，又能使学生联系实际学“活”；既能复习前面的旧知，又能为后面的新知做铺垫。因此，我们将思考题教学和新授课相融合，给学生制造“想”的事件，让学生在操作中想、合作中想、开放地想，让学生经历前思后想、融会贯通的思考旅程。

例如，在教学“解决问题策略——转化”时，我们将思考题作为问题提出，结束作为问题进行解决，通过转化策略的运用经历解决思考题的全过程，使学生既感受到转化策略的价值，又能更加清晰地体验到综合运用已有的策略来解决实际问题。

2.和练习课、复习课相整合，给学生创造“思考”的空间。

针对教材编排特点，我们将思考题和练习课、复习课进行整合，给学生创造“思考”的空间，让他们在有梯度的引导下，经历独立思考的过程，使每个学生的思维水平得到相应的发展。

（1）思考题和练习课整合。

例如，在学习完分数乘法后，通过有梯度的设计进行练习课教学，使学生尝到发现规律、运用规律解决问题的惊喜。

第一层次：通过一组有价值的口算，产生研究需求和研究素材。

第二层次：通过探索思考题的规律并运用规律解决问题。

第三层次：通过小课题研究进行自我发现。

算一算：下面每组数的和与积。

猜一猜：“和等于积”的两个分数，分子和分母可能会有什么特点？

验证一下：举出符合这样特点的两个分数是否“和等于积”？

（2）思考题和复习课整合。

以下面这道题为例。

寻找关系：三个正方形面积之间有什么关系？

发现规律：直角三角形三条边有什么规律？

追寻历史：介绍毕达哥拉斯在客人家里的地砖上发现勾股定理，杀了百头牛庆祝等相关故事。

文化熏陶：很多研究是来自日常生活中的发现，鼓励学生像数学家那样善于发现问题，探究问题。

二、开发思考题专题课，放大“思考题”的思考内涵

我们根据思考题本身的特点并结合教学进程因材而教，分四种专题对“思考题”进行开发，即对数学规律的探究、对策略的综合运用、对数学经验的积累、对数学思想的运用。

现以对数学思想的运用专题教学为例。学完《长方形和正方形》后，以“巧求周长”为主题，用分类思想展开教学过程，感受转化思想的奇妙。这节思考题专题教学可分三个板块。

板块一：学生用两个长5厘米、宽2厘米的长方形进行组合，然后分成两类。

板块二：探究周长是多少。

先探究拼成长方形的周长，并形成求这一类图形周长的一般方法。

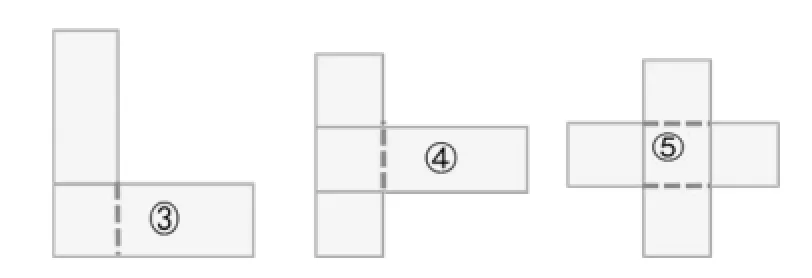
再探究不是长方形的周长，先研究3号图（思考题），呈现了四种不同思维含量的解决方案。最后优化提升，感受转化思想的价值。再方法迁移自我研究4号和5号图形。

板块三：拓展延伸。

拓展操作思考，刚才重叠的部分是正方形，如果重叠的部分不是正方形呢？

数学思考题专题课，以思维发展为核心，一堂课围绕一个主题，由三到四个不同形式的活动板块组成。学生在丰富多彩的活动中自主思考、探究交流、体验感悟、展示分享学习成果，教师通过点拨、梳理、串联，提升学习效益。特别是拓展延伸板块，促进了学生深度学习。

三、构建思考题学习新平台，拓展“思考题”思考空间

通过课堂进行思考题教学，是实施思考题栏目目标的重要路径。如何更好地满足学生个性化学习需求，让每个学生都能通过思考题经历数学思考的过程，放大思考题思考的价值？我们认为，可以制作“思考题”微视频供学生在线自主学习；可以利用数学主题拓展教学微信公众平台进行选择性学习；可以征集学生思考题中的困惑，利用班级和学校开设的学生讲坛和名师讲坛进行互动分享学习；也可以和家人、同学一起进行探讨式学习。通过这样构建没有固定圆心和半径的学生学习圈，让学生的学习随时都可以发生，思考无处不在。

例如，“学生数学讲坛”是学生分享思考经验的舞台，下面是“学生数学讲坛”关于思考题稿件的征集要求：下图是思考题，请学生仔细分析，可以从以下几个方面准备讲稿：4个和9个正方形摆成的图形周长是多少？周长之间的关系为什么是4+6、4+6×2？准备大一点的正方形摆给同学们看，第三个图形正方形有几个？周长是多少？你发现了什么规律？和大家分享解决这一类思考题有什么秘诀。