基于蒙特卡罗法的盐溶液密度测量不确定度评估

朱顺/ 上海马陆日用友捷汽车电气有限公司

基于蒙特卡罗法的盐溶液密度测量不确定度评估

朱顺/ 上海马陆日用友捷汽车电气有限公司

以蒙特卡罗法为基础，结合Minitab分析软件对盐溶液密度的测量不确定度进行评估。蒙特卡罗法除在测量模型是非线性、计算公式的偏导数求证困难或不方便等情况下评估测量不确定度有明显优势外，其在单一测量数据的不确定度评估中也有便利性，可以方便求出标准不确定度，并给出指定置信概率下的扩展不确定度。

盐溶液；密度；蒙特卡罗；测量不确定度；Minitab

0　引言

随着检测实验室技术能力的提升，实验室安全风险越来越受到实验室的关注［1］，测量不确定度作为技术能力的评价之一，备受重视。中国合格评定国家认可委员会（CNAS）认可文件［2］要求，实验室应有相应的测量不确定度评定能力。测量不确定度是根据所用的信息，表征赋予被测量值分散性的非负参数［3］。笔者以盐雾试验［4］过程中盐溶液密度为例进行测量不确定度评估。

1　盐溶液密度测量模型

根据实际配置情况，其计算公式为

式中：ρ —— 盐溶液密度，g/L；

m —— 称取的盐质量，g；

p —— 盐的纯度，%；

V —— 水的体积，L

式（1）中，m、p、V均为均匀分布，可见其输出函数ρ为非正态分布，尤其适用蒙特卡罗法（以下简称MCM）对其测量不确定度进行评估［5］。此外一般盐溶液配置过程中，无法实现重复测量，进而无法方便计算GUM［3］法的A类不确定度。

2　MCM实施

2.1MCM输入

分别使用电子天平、容量瓶对盐的质量和水的体积进行测量，测量结果见表1。

盐的称重质量为501.1 g，电子天平的最大允许误差为±0.5 g，均匀分布，因此盐的质量范围应是m～U ［500.6 g，501.6 g］。

水的体积为10 L，而容量瓶容积的最大允许误差为±2 mL，均匀分布；因此水的体积范围应是V～U ［9.998 L，10.002 L］。

根据盐的合格标签，其纯度为≥99.5%。该盐为分析纯，根据相关标准［6］，其不会达到优质纯等级（纯度≥99.8%），因此纯度应位于99.5%～99.8%，均匀分布，盐的纯度为p～U［99.5%，99.8%］。各输入量的分布情况见表2。

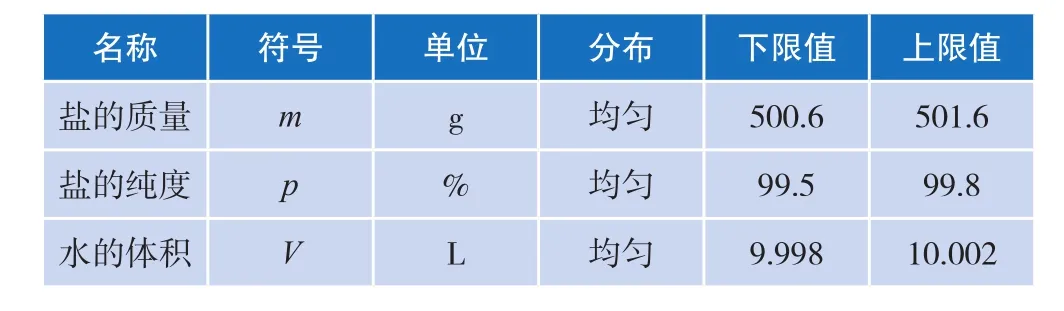
表2　各输入量的分布情况

2.2MCM传播

根据表2中的数据结合Minitab软件，随机生成106个样本量，得到106个互不相关的三个均匀分布数据组，作为模拟输入量，各模拟输入量的频数直方图见图1～图3。

2.3MCM输出

将随机生成的这三组数据量为106的数据，使用Minitab软件通过式（1）的运算规则计算盐溶液密度ρ，输出结果频数直方图如图4所示。使用Minitab软件对输出结果进行正态性检验，正态检验图如图5所示。输出量的PDF（概率密度函数）已较大程度偏离正态分布，其正态性检验p ＜ 0.005。该结果更加说明盐溶液密度的测量不确定度适合使用MCM法进行评估。

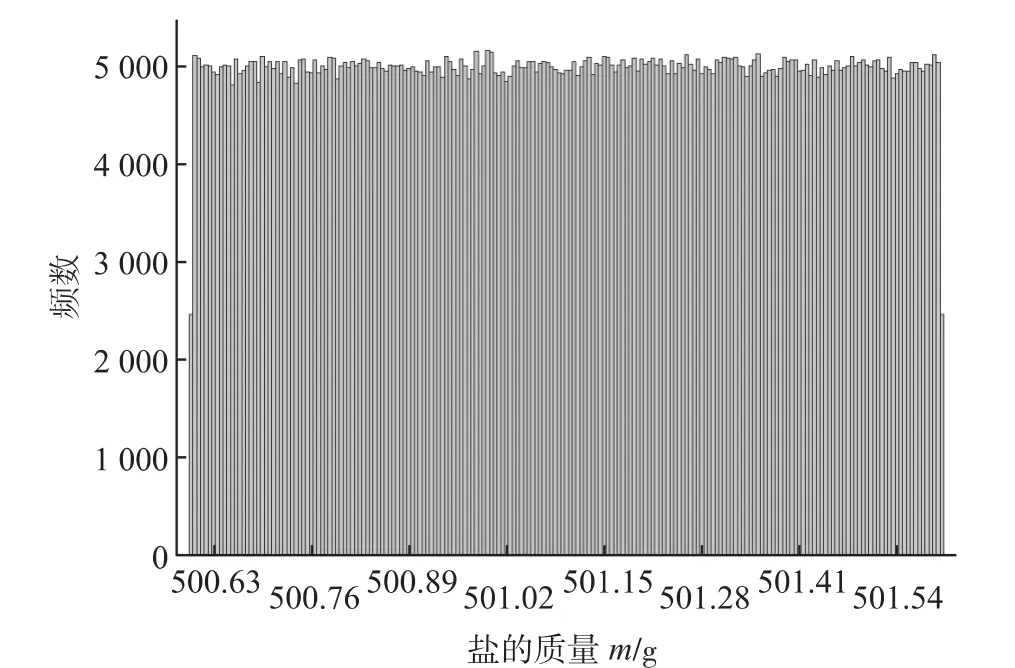
图1　盐的质量m频数直方图

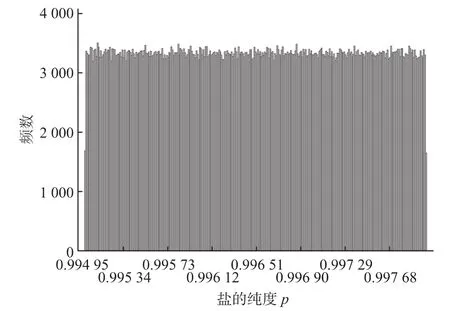
图2　盐的纯度p频数直方图

图3　水的体积V频数直方图

图4　盐溶液密度ρ频数直方图

图5　盐溶液密度ρ的正态性检验

2.4报告结果

根据MCM法对称区间评估要求：

对于置信概率为p，数据量为M，且输出的M个数据按非递减排列（考虑结果值相等的情况），如果pM为整数，设q = pM，否则取q为pM+1/2的整数部分。则［ylow，yhigh］为Y的概率p的包含区间，其中，对任意的r = 1，2，…，M - q，ylow= y（r），yhigh= y（r+q）。

如果（M - q）/2为整数，取r =（M - q）/2，否则取r为（M - q+1）/2的整数部分，可得概率对称包含区间［y（r），y（r+q）］。

根据图5中的数据：

标准偏差s = 0.05 g/L

使用Minitab对输出结果进行递增排列，取置信概率为95%，数据量为106个，因此：

p = 95%，M = 106，

pM = 950 000，为整数

故q = 950 000

（M - q）/2 =（1 000 000-950 000）/2=25 000，为整数

故r = 25 000

r + q = 975 000

查Minitab递增排列的数据中

ρ25000= 49.84 g/L

ρ975000= 50.02 g/L

因此置信概率为95%的包含区间为［49.84 g/L，50.02 g/L］，即本次盐溶液密度标准不确定度为u = 0.05 g/L，扩展不确定度U95= 0.09 g/L。

3　结语

GUM法通常进行重复性测量，之后使用重复性测量数据进行测量不确定度的A类评估，对于单一测量数据的不确定度评估，尤其是破坏性的单一数据，因无法进行重复性测量，进而无法方便评估其A类不确定度。GUM法一般通过计算测量模型偏导数的方法求出不确定度传播率，这对于有些不方便计算测量模型偏导数的情况则不适用。此外有些实验室无法完全识别或者不能识别主要的测量不确定分量来源。以上诸因素给实验室使用GUM法实际评估测量不确定度带来困难。

MCM法常用于［5］：①避免应用不确定度传播率时，或该测量模型的偏导数计算困难；②输出量的PDF（概率密度函数）已较大程度偏离正态分布；③数学模型为非线性。

由于盐溶液密度测量输出量的PDF已较大程度偏离正态分布，而且盐溶液测量模型通常被简化处理，然后使用单一测量值或多组数据平均值代入进行计算求得传播系数，因此盐溶液密度适合使用MCM法进行测量不确定度评估。

综上所述，对于一组测量数据，尤其是测量模型输出量的PDF较大程度偏离正态分布时，建议实验室采用MCM法评估测量数据的不确定度。

［1］ 左鹏飞，骆海清，周利英，等. CNAS认可实验室质量安全风险管理［J］. 理化检验-物理分册，2014，50（5）：614-617.

［2］ 国家认证认可监督管理委员会. CNAS-CL01：2006检测和校准实验室能力认可准则［S］.北京：2006.

［3］ 全国法制计量管理计量技术委员会. JJF 1059.1-2012 测量不确定度评定与表示［S］.北京：中国计量出版社，2012.

［4］ 全国金属与非金属覆盖层标准化技术委员会（SAC/TC57）. GB/ T 10125-2012人造气氛腐蚀试验 盐雾试验［S］. 北京：中国标准出版社，2012.

［5］ 全国法制计量管理计量技术委员会. JJF 1059.2-2012 用蒙特卡罗法评定测量不确定度［S］. 北京：中国计量出版社，2012.

［6］ 全国化学标准化技术委员会化学试剂分会（SAC/TC63/SC3）. GB/T 1266-2006 化学试剂 氯化钠［S］. 北京：中国标准出版社，2006.

新产品介绍

Evaluation of measurement uncertainty of salt solution density based on Monte Carlo method

Zhu Shun
（Shanghai Malu Ri Yong JEA Gate Electric Co.，Ltd.）

Based on Monte Carlo method and Minitab analysis software，the measurement uncertainty of salt solution density is evaluated. Besides obvious advantages in situations of the nonlinear measurement model and diffcult or inconvenient partial derivation of the calculation model，Monte Carlo method has also advantages in the uncertainty evaluation of a single measurement data. It is very convenient to determine the standard uncertainty and give the expanded uncertainty of confdence probability.

salt solution； density； Monte Carlo method； measurement uncertainty； Minitab