RA 网络多协同排序算法模型及算法研究

谢 婷

（安徽省马鞍山市委党校，安徽马鞍山243011）

RA 网络多协同排序算法模型及算法研究

谢 婷

（安徽省马鞍山市委党校，安徽马鞍山243011）

针对当下约车平台迅猛发展的态势，就其中广泛关注的问题——RA网络多协同排序问题进行了探究。针对滴滴出行的实际数据，将RA网络多协同排序问题转化为求解数学模型两个评价指标最优解的问题，基于传统的免疫算法（generate and test）的相关概念，融合半解析解的相关思想，构建一种优化算法GBFA（Generate Bacterial Foraging Algorithm），进而提出了基于GBFA算法的RA网络多协同排序算法，并据此开发RA网络多协同排序软件”RA－LC”。以滴滴出行北京市2015年5月—2016年4月的数据为对比对象，利用RA－LC对相关实例进行仿真，结果显示该算法对于时间预测具有较高的准确度，对于RA网络多协同排序问题具有极佳的适用性和精确度。

多协同排序；Mathematica；GBFA；滴滴出行；时间预测

0 引言

网络约车平台的迅猛发展已悄然改变了人们的生产、生活方式［1］。客户发单（request）与司机的应答（answer）涉及到复杂的排序问题，在同一片区往往存在着多名司机，司机彼此之间的线路相互影响，使得request－answer网络（RA网络）极其复杂，应加强RA网络的关联性，进而凸显出多协同排序算法研究的重要性和必要性［2－3］。

鉴于此，国内外学者对RA网络的多协同排序算法进行了大量研究。Cui J X、Shen H［4－5］等人利用GPS定位对司机位置进行的计算，通过对司机当前行进数据进行拟合，计算出司机达到客户发单（request）位置的时间，依照到达时间的长短由低到高排序，但文献［4］和文献［5］仅仅考虑了当前数据的效用，没有将堵车、迟缓度加入协同决策方案中。Petrovic′M［6］基于改进后的粒子群算法，将行进过程中的堵车问题以概率的形式加入到决策函数中，排序的结果更加有效，但是文献［6］依旧没有利用历史数据，导致排序仿真的结果与实验结果有较大的出入。Huang X［7］、Jianxun Cui［8］等人基于优步约车平台的运行数据，对于RA网络进行多变量的数据拟合，从而为排序提供支持，但是文献［7］和文献［8］所使用的拟合模型仅仅是多项式拟合，导致了误差较大，量纲不统一。SAVCHENKO［9］基于量纲分析法，依照的司机行车历史数据进行数据拟合，但拟合模型仅仅是多项式拟合，导致了拟合结果与真实情况相差较大。

本文在前人的研究基础上，选用细菌觅食算法（简称BFA，下同），同时基于免疫算法（generate and test）的相关概念，融合半解析解的相关思想［10］，针对BFA算法的3个操作环节（复制操作环节、趋向性操作环节和迁移操作环节），提出BFA的一种优化算法GBFA（Generate Bacterial Foraging Algorithm）：将趋向性操作环节中的步长变为非固定步长，可以随着计算的进行而改变，建立趋向性操作步长的动态更新机制；此后，利用免疫算法（generate and test）替换BFA的复制操作环节，针对细菌群落进行筛选，将其中适应度较高的细菌复制并替换适应度较低的细菌；最后，在迁移操作环节中，适应度最高的个体被驱散的概率为0，适应度其他的个体被驱散的概率为Ped。利用GBFA算法，针对RA网络建立了以最短接车时间为目标函数的数学模型，并注重考虑了堵车、司机迟缓、司机到达后客户寻车等因素，构建完整的RA网络多协同排序模型。并利用滴滴出行的历史数据进行仿真验算，验证本文所提出的RA网络多协同排序模型的适用性和算法的优越性，以期为当下约车平台提供更加合理的排序模型。

1 模型构建

1．1 问题定义

客户打开滴滴出行APP，滴滴出行APP自动定位客户的位置，客户输入目的地后进行“呼叫”操作，这便是发单（request）；滴滴出行APP将request命令导入云处理器并传送给某位司机，该司机接单后便完成了一次应答（answer）。

自司机应答（answer）并送客户至目的地为一次MISSION，整个事件耗时为TIME。

滴滴出行APP将某个城市划分成为n个区域，该城市区域的集合为D，被划分的区域为d，则有

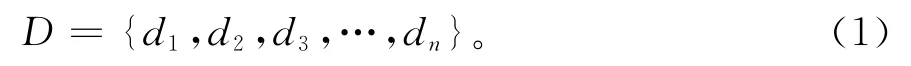
将一天的时间划分为144个时间片｛t1，t2，t3，…，t144｝，每个时间片的长度为10min。对于区域di，在时间片tj，有rij个客户request，同时有aij个司机成功进行了aij次answer；对于区域di，在时间片tj，需求demandij，供给supplyij＝aij，供需缺口gapij可以表示为

1．2 评价指标

对n个区域和q个时间片，对于区域di，在时间片tj，供需缺口为gapij，算法计算出缺口为sij，以MAPE作为排序计算精度的评价指标

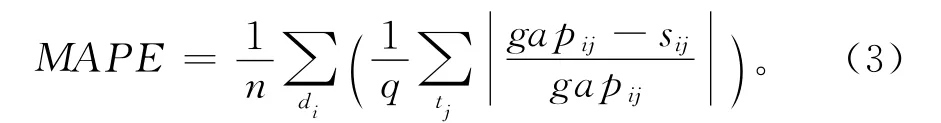
以TIME的最优解作为排序计算效用的评价指标。

2 算法简介

将RA网络多协同排序模型问题转化为求解两个评价指标最优值的问题，以下利用GBFA算法进行解答。

2．1 GBFA算法的基本思想

BFA中第i次的步长为

式中：Ns为BFA虚拟的细菌群落中细菌游动的最大次数；Led为细菌游动的初始步长。

细菌移动的每一次步长均小于初始步长Led。并且，计算开始之时（i值较小），第i次的步长Ci很大，可以提高搜索的速度，使得计算可以更快进行；随着计算过程的进行（i值的增大），第i次的步长Ci会越来越小，这是为了在计算的后期，保证足够的收敛精度。

在趋向性操作步长的动态更新机制建立之后，将群落中所有细菌的适应度进行累加，并按从大到小的顺序进行排列，形成细菌序列。将细菌序列前m（m为百分比）部分的细菌进行n次复制，将细菌序列中的其余细菌进行剔除，m和n的关系为

如此一来，细菌群落中m部分的细菌代表了原有的细菌菌落，可以提高细菌群落的整体觅食能力。此后，依照如下步骤对细菌菌落进行变异、繁殖：

1）挑选出细菌群落中适应度较高的细菌，标记为克隆群体A；

2）克隆群体A繁殖成为群体B：

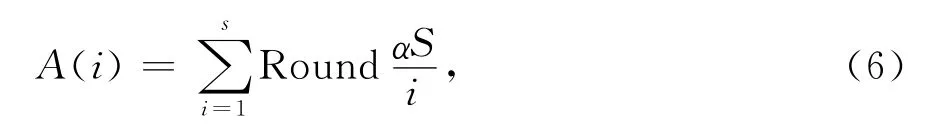
式中max为取最大值函数。

3）对群体B进行变异操作，生产群体C：

式中：random为随机函数；B（i）为计算的克隆群体的个数；β为变异概率β，计算方法为

根据式（6）可知，适应度越高的个体，变异概率β越大。

因为交叉方法

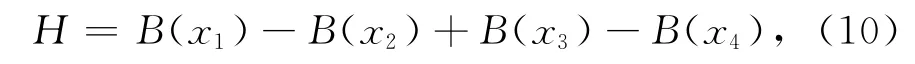
式（7）中，x1、x2、x3、x4为克隆群体中4个不同的细菌。将群体C融合进入群体B中，形成群体D：

4）对群体中，将其中前m（m为百分比）部分的细菌进行n次复制，将其余细菌进行剔除。

在传统的BFA算法之中，需要设定一个迁移概率Ped，如果随机数小于迁移概率Ped，就会对细菌进行迁移操作。这样做的目的是希望细菌可以跃出局部最优解的陷阱。但是，这种做法同样具有极大的弊端，因为迁移概率Ped对于所有的细菌都有效，无论细菌的适应度如何，都可能被迁移。GBFA算法在迁移操作环节中，适应度最高的个体被驱散的概率为

式中：Round为四舍五入函数；S为细菌群落的整体个数；A（i）为计算的克隆群体A的个数；i为第i次计算；α为克隆的系数。

为了方便计算，将适应度F进行标准化0，适应度最高的个体被驱散的概率为Ped，以提高搜索的速度。

根据以上思想，绘制GBFA算法流程图，如图1所示。

图1 GBFA算法流程图

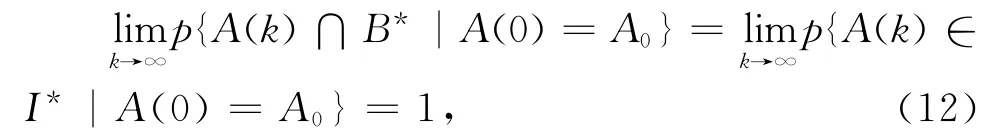
化简得到

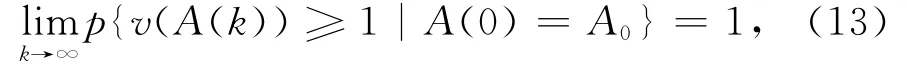
2．2 GBFA算法的敛散性

DASGUPTA对BFA算法的敛散性进行了研究［11－12］，但是DASGUPTA没有考虑BFA算法模拟菌群内部各个细菌个体之间的影响。笔者提出的GBFA虽然没有触及到传统BFA算法的定义基础，但是由于免疫算法的加入，需要重新证明GBFA的敛散性。

根据李涛［13］的研究：对于抗体种群A0，抗体空间几何为I＊，v（A（k））为计算所得最优解的个数，B为最优解的个数，

便可以称之为该算法收敛到最优解集的概率为1。故而，当算法迭代数量达到一定程度时，便一定会收敛。

GBFA引入了免疫算法，对于抗体种群A0，有

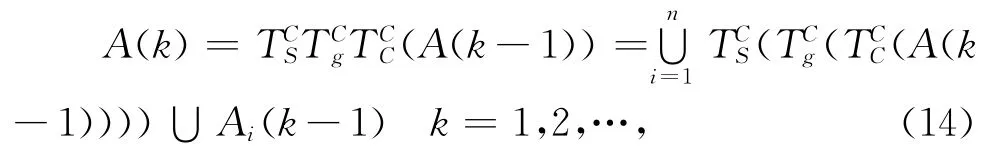
式中Ai（k）表示细菌i在第k次操作的时候所在的位置，而Ai（k）是由Ai（k－1）经过克隆、变异而得。

为了方便表述，标记

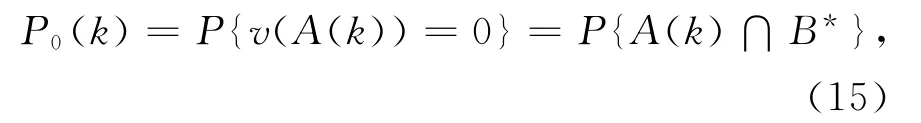
则有

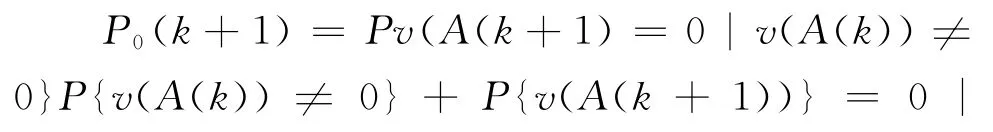
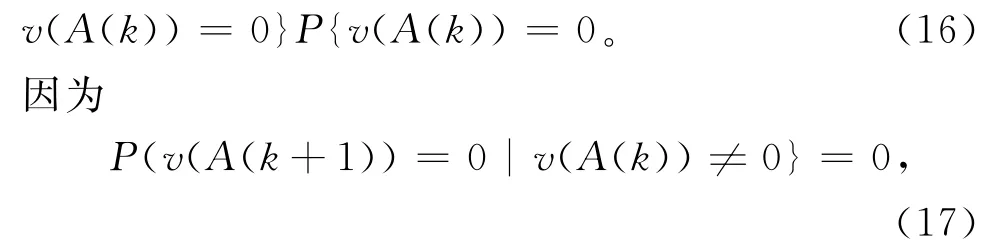
则有

所以

故而

因为

所以

所以

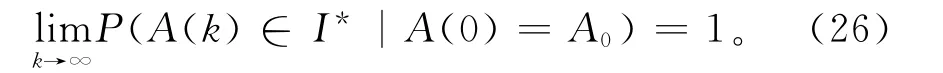
综上所述，GBFA以概率1收敛。

2．3 拟合方案

针对历史数据而对未来做出预测，其数学原理为函数的拟合，对于拟合函数模型的优化，基于智能算法［14］。本文利用Mathematica来进行拟合模型的优化，利用GBFA算法对优化结果进行排序。Mathematica是Stephen Wolfram开发的一套计算机代数系统，可以对数据的拟合函数模型进行自动优化。

选取实验函数

其中，RandomVariate［NormalDistribution［0，0．2］］的作用是加上一个均值为0、标准差为2的正态分布随机噪声，x∈［－10，10］。计算结果为

通过GBFA算法对上述10个拟合模拟进行误差计算，选取误差最小的拟合模型：1．134 935 310 743 823 1＋cosx＋1．964 926 975 541 333 4sin（x）cos（x），拟合结果如图2所示。

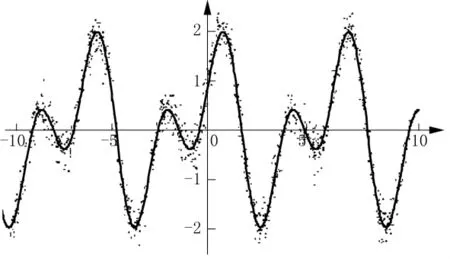
图2 5拟合模型的自动优化

根据图2，发现拟合效果颇佳。

3 排序实现方法

根据问题模型和GBFA算法，开发RA网络多协同排序软件”RA－LC”，现就其中的计算流程进行简要说明。

步骤1：以客户当前位置为目的地，以附近i名滴滴出行司机的位置为出发点，寻找出i名滴滴出行司机的位置和客户当前位置之间所有可行的路径，按照路径长度基于GBFA算法进行排序，各自选中序列前j种路径方案，共ij种路径方案。

步骤2：调取该i名滴滴出行司机在时间片tk接单之后，选用第j条路径方案前往客户当前位置的时间的历史数据，利用GBFA算法进行排序并选择最优拟合模型，计算得出该次该i名滴滴出行司机在时间片tk接单之后，选用第j条路径方案前往客户当前位置的时间为tijk，0。

步骤3：调取该i名滴滴出行司机在时间片tk发车前往客户当前位置之后，选用第j条路径方案至客户当前位置的平均速度的历史数据，利用GBFA算法进行排序并选择最优拟合模型，计算得出该次该i名滴滴出行司机在时间片tk发车前往客户当前位置之后，选用第j条路径方案至客户当前位置的平均速度为vtjk，0。

步骤4：调取第j条路径方案在时间片tk突发堵车的频率以及时间的历史数据，利用GBFA算法进行排序并选择最优拟合模型，计算得出该次选用第j条路径方案在时间片tk突发堵车的概率Pjk，0以及时间tjk，0。

步骤5：计算该i名滴滴出行司机选用第j条路径方案到达客户当前位置的时间Tij，0

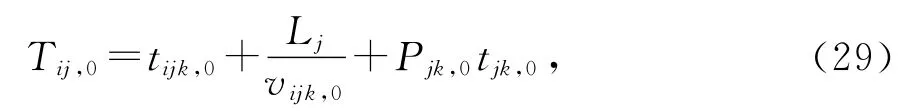
式中Lj为第j条路径解决方案的长度。

步骤6：在第i名司机到达客户当前位置且客户上车之后，以客户当前位置为出发点，寻找出客户出发点和目的地之间所有可行的路径，按照路径长度基于GBFA算法进行排序，选中序列前J种路径方案。

步骤7：调取该i名滴滴出行司机在时间片tk＋Tij0接客户之后，选用第J条路径方案前往客户目的地的时间的历史数据，利用GBFA算法进行排序并选择最优拟合模型，计算得出该次该i名滴滴出行司机在时间片tk＋Tij，0接客户之后，选用第J条路径方案前往客户目的地的时间为tijk，1。

步骤8：调取该i名滴滴出行司机在时间片tk＋Tij，0发车前往客户目的地之后，选用第J条路径方案至客户目的地的平均速度的历史数据，利用GBFA算法进行排序并选择最优拟合模型，计算得出该次该i名滴滴出行司机在时间片tk＋TiJ，0发车前往客户目的地之后，选用第J条路径方案至客户目的地的平均速度为viJk，1。

步骤9：调取第J条路径方案在时间片tk＋TiJ，0突发堵车的频率以及时间的历史数据，利用GBFA算法进行排序并选择最优拟合模型，计算得出该次选用第J条路径方案在时间片tk＋TiJ，0突发堵车的概率PJk，1以及时间tJk，1。

步骤10：计算该i名滴滴出行司机选用第J条路径方案到达客户目的地的时间TiJ，1

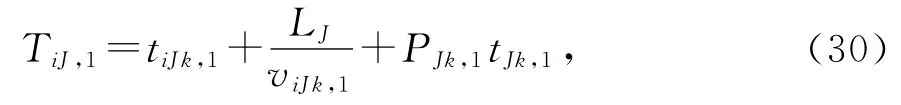
式中LJ为第J条路径解决方案的长度。

步骤11：i名滴滴出行司机选用第j条路径方案到达客户当前位置，并选用第J条路径方案到达客户目的地，整个MISSION的耗时TIMEijJ

步骤12：利用GBFA算法对序列TIMEijJ进行排序，寻找出最优方案TIMEmin

4 仿真实验

以滴滴出行北京市2015年5月—2016年4月的数据为对比对象。快车是滴滴出行推出的一种较为快捷的出行方式，司机以单注册客户（但注册客户可能一人乘车，也可能多人乘车）为服务对象的服务方式。2015年9月16日21点37分有单注册客户以快车形式request，客户的当前位置为天坛南门，目的地为北京市昌平区潢京客栈主题宾馆（图3）。

利用RA－LC软件计算7位司机在本次MISSION的TIME（图4）。

2015年9月16日21点37分4号滴滴出行司机answer，选用的路径与GBFA算法计算路径相同，2015年9月16日22点41分4号滴滴出行司机完成此次MISSION，耗时64min。由此可见，GBFA算法的计算精度极高，对于TIME的预测极为精确。

为了进一步验证GBFA算法对更为广泛的时间片的适应性，选取2015年9月15日、2015年10月15日、2015年11月15日、2015年12月15日、2016年1月15日共5日的数据作为研究范围，每个时间片（10min）选取10个answer，共7 200单出行数据，利用RA－LC软件计算每次MISSION的TIME（图5），与实际的TIME相比较，分析其误差N。

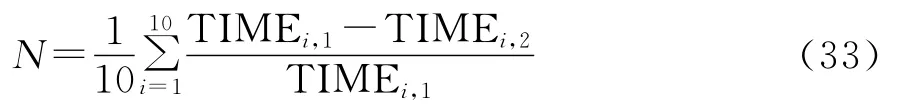
式中：N为每个时间片10组数据的误差的平均值；TIMEi，1为时间片内实际的i单MISSION的TIME，TIMEi，2为时间片内利用RA－LC软件计算的i单MISSION的TIME。

图3 GBFA算法计算路线与客户当前位置的车辆

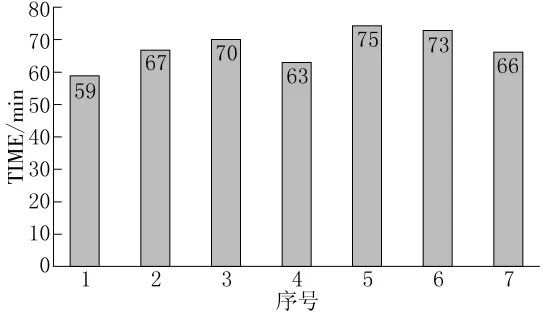
图4 利用RA－LC计算而得的7位司机的TIME

通过图5可以看出，RA－LC软件计算的MISSION的TIME与实际的误差较小，均在－0．06～0．06。说明RA－LC软件对于宽时间跨度的滴滴出行排序模型具有较高的精度。此外，无论是哪个月份，RA－LC软件计算的MISSION的TIME与实际的误差值随时间片的变化是不规则的，说明RA－LC软件不受时间的约束，具有极高的适用性。

图5 N的分布情况

5 结语

本文改进传统的细菌觅食算法提出GBFA算法，将GBFA算法应用到RA网络多协同排序模型中，并开发计算程序RA－LC，对滴滴出行2015年 5月—2016年4月的数据进行对比，结论显示：

1）利用Mathematica软件对于拟合模型进行优化，并利用GBFA算法对优化模型进行排序，选取其中最优拟合模型，对于预测司机选用第j条路径方案前往客户当前位置的时间为tijk，0、选用第j条路径方案至客户当前位置的平均速度为vijk，0、选用第j条路径方案在时间片tk突发堵车的概率Pjk，0以及时间tjk，0具有颇佳的准确度。

2）通过单次MISSION，利用RA－LC计算其TIME，并与实际的TIME进行对比，两者相差近1 min，说明RA－LC对于单次MISSION具有极高的精确度。

3）选取更加宽的时间范围，利用RA－LC计算其TIME，绘制的分布图，显示基于GBFA算法RA网络多协同排序模型对于解答RA网络多协同排序问题具有极佳的适用性，而且N与时间并无明显的比例关系，说明基于GBFA算法RA网络多协同排序算法并不受时间的影响。

［1］刘亚秋，吴双满，韩大明，等．基于云计算的手机智能出租车呼叫系统［J］．计算机工程，2014，40（4）：14－18．

［2］王超学，田利波．一种改进的多目标合作型协同进化遗传算法［J］．计算机工程与应用，2016，52（2）：18－23．

［3］孟祥豪，罗景青，马贤同．一种基于多站测向和多参数信息的联合分选算法［J］．控制与决策，2016，31（1）：160－164．

［4］Cui J X，Liu F，Janssens D，et al．Detecting urban road network accessibility problems using taxi GPS data［J］．Journal of Transport Geography，2016，51：147－157．

［5］Shen H，Li Z，Qin J，et al．Changes in functional connectivity dynamics associated with vigilance network in taxi drivers［J］．Neuroimage，2016，124（Pt A）：367－378．

［6］Petrovic′M，Sadowski J T， iber A，et al．Wrinkles of graphene on Ir（1 1 1）：Macroscopic network ordering and internal multi－lobed structure［J］．Carbon，2015，94：856－863．

［7］Huang X，Zhao Y，Ma C，et al．TrajGraph：A Graph－Based Visual Analytics Approach to Studying Urban Network Centralities Using Taxi Trajectory Data．［J］．Visualization ＆Computer Graphics IEEE Transactions on，2016，22（1）：160－169．

［8］Jianxun Cui，Feng Liu，Davy Janssens，et al．City－Wide Examining Transport Network Accessibility Using Taxi GPS Data［C］／／Cota International Conference of Transportation Professionals．New York：American Society of Civil Engineers，2015．

［9］SAVCHENKO，VYACHESLAV．Future Developmentof E－Commerce in Russia and Germany［D］．Valencia：University of Applied Sciences Valencia，2015．

［10］王俊奇，李闯，董晔．Bishop法的半解析解及其广义数学模型［J］．水利与建筑工程学报，2015（6）：123－128．

［11］Tang W J，Li M S，He S，et al．Optimal Power Flow With Dynamic Loads Using Bacterial Foraging Algorithm［C］／／Power System Technology，2006．PowerCon 2006．International Conference on．IEEE，2006：1－5．

［12］DAS S，BISWAS A，DASGUPTA S，et al．Bacterial Foraging Optimization Algorithm：the Oretical Foundations，Analysis，and Applications［C］∥Foundations of Computational Intelligence Volume 3．Berlin／Heidelberg：Springer，2009：23－55．

［13］李涛．计算机免疫学［M］．北京：电子工业出版社，2004．

［14］Li L，Zhang B，Li W，et al．Orthogonal polynomial function fitting for hyperspectral data representation and discrimination［J］．Pattern Recognition Letters，2016（1）：56－58．

The Model and Algorithm Research on RA Network More Collaborative Sorting Algorithm

XIE Ting
（Party School of Maanshan City Anhui Province，Maanshan Anhui 243011，China）

A issue got a wide range of concern in the research circle——RA more cooperative network scheduling based on the current rapid development car booking platform．As for the actual travel data bit， the RA network more collaborative problem solving scheduling problems have been changed into two optimal solutions to mathematical model evaluation．Based on the related concepts on traditional immune algorithm（generate and test），combined with semi－analytical solution，an optimization algorithm GBFA（Generate Bacterial foraging algorithm）has been established．Furthermore，an RA network more collaborative sorting algorithm based on GBFA algorithm has been proposed，and an“RA－LC”more collaborative sorting software has been developed．Taking Didi travel data in Beijing from May 2015to April 2016as the contrast object，the relevant examples has been simulated by using RA－LC software．The results show that the algorithm has higher temporal prediction accuracy，and has an excellent applicability and accuracy for the issue of RA more cooperative network sorting．

multi－coordinated sorting；MATHEMATICA；GBFA；Didi travel；time predict

TP391

A

1009－8984（2016）02－0119－07

10．3969／j．issn．1009－8984．2016．02．030

2016－03－25

谢婷（1975－），女（汉），安徽马鞍山，硕士，讲师主要研究计算机信息技术、网络应用。