岩体爆破震动的监测与衰减规律
2016-08-17李雄伟李欣杭重庆交通大学土木工程学院重庆400074
李雄伟,李欣杭(重庆交通大学 土木工程学院,重庆 400074)
岩体爆破震动的监测与衰减规律
李雄伟,李欣杭
(重庆交通大学 土木工程学院,重庆 400074)
为研究爆破震动波在岩体及减震孔中的传播及其影响,本文以重庆两江新区SK厂区周边土石方爆破工程为例,运用ANSYS/Ls-dyna软件和萨道夫斯基经验公式,计算出现场地质条件下的场地系数 K = 4 724.98,衰减系数 α = 1.9955,并通过现场试验,测算了减震孔前后地表质点振动速度,最后将现场试验数据与数值模拟结果进行对比分析.结果表明:现场试验结果与数值模拟有一定的差异,但存在同样的变化规律.
岩体爆破;减震孔;质点震速;衰减规律
岩体在爆炸动力的瞬间冲击荷载作用下,爆炸冲击波和应力波向四周传播,使岩体产生变形和破坏.在早期的研究中,国内外学者主要关注的是爆破地震波的震速及其峰值的作用,以现场监测数据回归分析得出的萨道夫斯基公式为代表的爆破地震波传播衰减经验公式得到广泛应用[1].李保珍[2]、韩子荣[3]、于亚伦[4]等以地面质点震动速度或加速度为测试参数对地面震动及其爆破地震波的衰减规律进行了研究,建立以萨道夫斯基公式为参考的区域性的爆破地震波参数随药量和距离及地形参数和地质条件衰减的经验公式.在高差和地形对爆破地震波的传播规律影响方面的研究也取得许多成果.目前,国内学者对爆破地震波的传播规律研究主要是围绕应力波在节理裂隙岩体中进行的.如张奇[5]对应力波垂直于节理入射时的传递过程进行了分析,认为应力波垂直节理面传播时,其应力衰减与两侧介质的物理力学性质的匹配有关.综上,国内外在爆破领域的研究已经较为成熟.
研究爆破振动的主要目的是探索爆炸作用下地震波的传播规律及建(构)筑物的响应情况,确定适合的爆破方案,指导爆破设计与施工,确保施工安全.本文主要分析爆破震动波在岩体与减震孔中的传播规律,并分析减震孔前后质点震动速度变化,最后与ANSYS数值分析结果对比,找出理论计算与数值模拟的异同点.
1 工程概况
SK是一家生产锂电正极材料的韩资企业,位于重庆市两江新区龙兴工业园区.由于重庆两江新区建设大开发,在SK厂区周围存在待开发用地平场爆破和道路建设爆破施工,对厂区的生产线影响较大,因此需进行爆破震动控制研究.
开挖爆破施工时,必须对爆源点周边振动敏感建(构)筑物、岩土体进行振动监测,严格控制质点振动强度,防止爆破振动对建(构)筑物、岩土体造成损伤或破坏.相关爆破振动控制标准见文献[6].一般当质点振速超过允许值时应暂停爆破作业,并通过爆破试验控制爆破药量与安全距离.
由于SK项目是锂电池正极材料的生产厂家,其中有大型的精密仪器,经当地专家研讨,其爆破振动控制标准为5 Hz以上、0.1 cm/s以下,控制标准非常高.经过综合分析,在SK厂区周边加设双排错位的减震孔(减震孔平面布置见图1).利用空心孔对爆破震动的减震作用,一方面可以保证SK厂区生产线的正常作业,另一方面也保证SK厂区周边爆破施工的有序进行.

图1 减震孔平面布置图
2 研究方法与原理
爆破震动强度的质点震动速度和频率与爆区最大一段装药量、爆心距、地质地形条件密切相关.爆破过程中,最大限度地减少爆破震动对周边建筑物的影响为施工关键所在.通过运用萨道夫斯基经验公式推断出围岩中K、α值,以确定单段最大炸药量,正确指导爆破施工,成功地控制爆破震动速度.萨道夫斯基地震动最大速度经验公式0:

式中:V为质点最大速度,单位cm/s;Q为齐爆药量,单位kg;R为爆心距,单位m;K为场地系数,α为衰减系数.对上式两边取对数,则得:


式(3)为一元线性回归方程,K、α为回归方程的回归系数.
根据最小二乘法,将各监测点的质点震动速度值V及齐爆药量Q、爆心距R分别代入上式,进行回归分析计算,得到该地质与地形条件下的K和α值.
3 现场试验
根据岩土工程勘察报告,SK厂区附近地质构造位于大盛场向斜北西翼,为单斜岩层产出,岩层产状为:倾向122°,倾角9°.层面裂隙不发育,局部有泥化现象,结合很差,属软弱结构面.厂区附近上覆土层为第四系全新统人工素填土(Q4ml)、粉质粘土(Q4dl+el);下伏基岩为侏罗系中统沙溪庙组(J2S)砂质泥岩、砂岩、粉砂岩层.
通过在距SK厂区350 m的贵格土石方平场程两江总部城做试爆试验,并严格按照SK厂区精密仪器爆破控制标准0.1 cm/s,TC-4850N爆破测震仪来监测SK厂区地面质点的震动速度.在试爆过程中,先从最小炸药量2 kg开始试爆,通过TC-4850N爆破测震仪监测SK厂区地表质点震动速度峰值,逐步增加炸药量,使SK厂区地表质点震动速度峰值接近0.1 cm/s.
按照以上的标准,在控制的试爆炸药量之间重复做了20次试爆试验,用TC-4850N爆破测震仪测得20组数据如表2.

表2 试爆试验结果
4 理论计算
根据试爆的数据,结合式(1)、(2),就能够将V、Q、R、K及α转换为线性关系,其中 y = l g V,x=lg(Q1/3/R).应用Excel软件进行函数拟合,结果见图2.

图2 lgV与 l g(Q1/3/R)的线性关系
因为 R2> 0 .99,所以这是一个线性特征非常明显的实验模型,由图2可得拟合方程为:
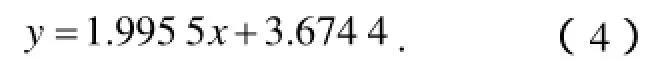
因此,lg K=3.674 4,α = 1 .9955,解得:
K=4 724.98,α =1.9955.
这样,通过本次试爆试验,就求得了SK厂区周围地形地质条件下的萨达夫斯基经验公式中的参数K和α.随着施工的进行,爆破震源位置变化,爆心距发生改变,利用计算得到的K、α,反算炸药量,控制施工中最大炸药量不超过这个值,指导后续爆破作业安全可靠的经行.
5 数值模拟
由于现场试验受各种自然因素影响,得到的结果具有一定的不确定性.计算机仿真模拟爆破过程可以验证现场试验结果的准确性,同时,可以从两种方法的差异中找到各自的不足,以便在后续研究中不断优化改进.

图3 网格划分后的三维模型
本文采用ANSYS/Ls-dyna进行模拟分析,由于模型四周无限延伸,故在模型四周及地面施加无反射边界条件,模型的上表面为自由面[7].整个模型采用mm-g-ms单位制,网格划分后的三维模型如图3.
施加约束后,设置好能量控制选项、文件输出和步数.最后生成K文件,修改K文件中炸药和空气的材料参数,添加炸药的状态方程及其爆点位置[8-10].
利用LS-DYNA的后处理器LS-Prepost,取10个不同断面,得到10组减震孔前后质点各方向震动速度峰值列于表3和表4.

表3 孔前各断面质点不同方向震动速度峰值
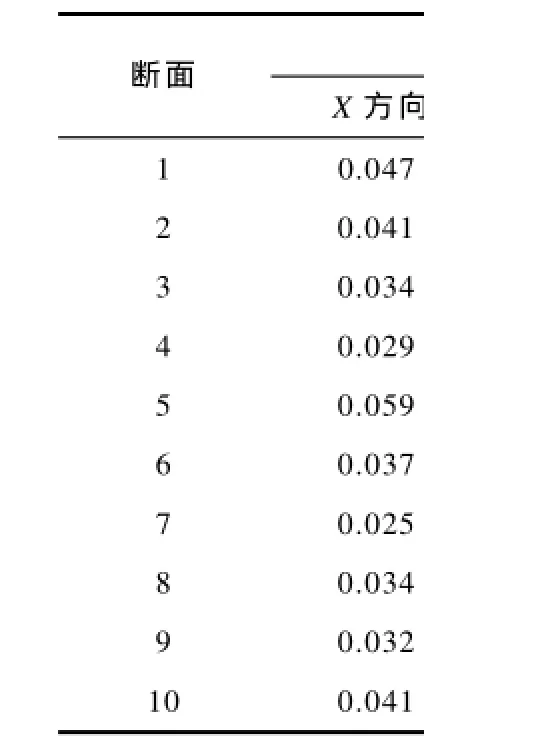
表4 孔后各断面质点不同方向震动速度峰
6 现场试验与数值模拟对比分析
前两节分别用现场试验和ANSYS/LS-DYNA数值模拟得到了SK厂区地表质点的速度.为了进一步探讨数值模拟结果正确与否,下边对两种方法得到的质点震动速度进行对比分析.图5是现场试验和数值模拟得到的减震孔前质点震动速度峰值,图6是现场试验和数值模拟得到的减震孔后质点震动速度峰值.
由图4和图5可以看出,数值分析得到的质点震动速度和现场试验得到的质点震动速度是有差异的,且总体上看,数值模拟得到的质点速度峰值都大于现场试验得到的质点速度峰值.除此之外,现场试验是在SK厂区精密仪器爆破控制要求0.1 cm/s的严格控制下实施的,得到的质点震动速度峰值满足精密仪器的爆破控制要求.而数值模拟得到的结果,部分质点震动速度峰值大于0.1cm/s,这主要是在模拟时,对模型的简化造成的[11].同时,这也是数值模拟的不足之处[12].

图4 孔前质点震动速度峰值对比
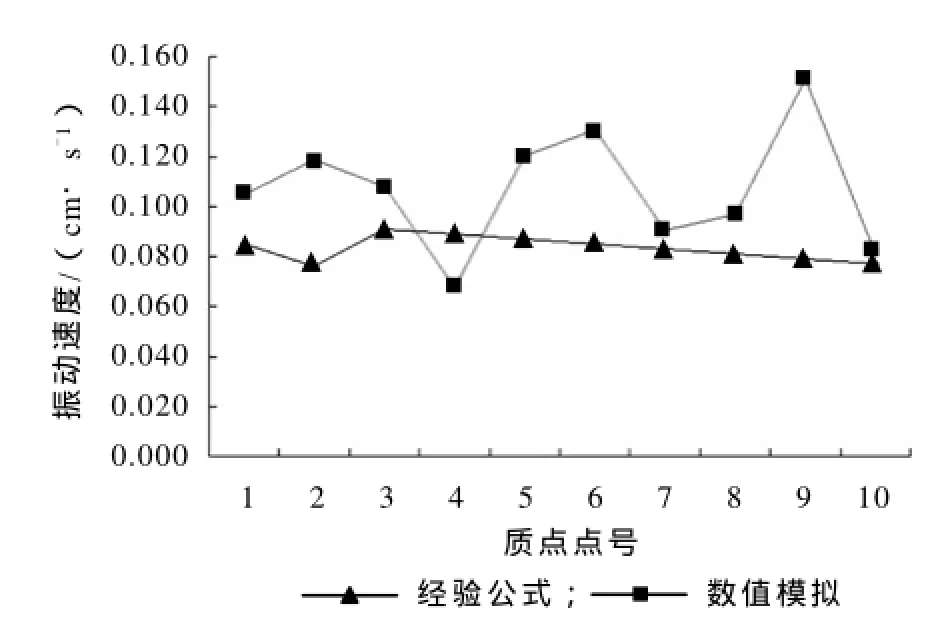
图5 孔后质点震动速度对比
7 结论
随着城市的不断发展,爆破施工变得越来越常见,本文的研究结果有助于指导爆破施工以及对周边建筑物的保护.由于现场自然因素复杂多变,存在许多现场试验和数值模拟考虑不到的因素,在以后的研究过程中仍需不断深入细化.
[1]言志信,言浬.应用人工神经网络预报爆破地震动峰值[J].铁道学报,2010,32(5):140-143.
[2]李保珍.露天深孔爆破地震效应的研究[J].长沙矿山研究院季刊,1989,9(4):32-37.
[3]韩子荣.金川—矿区露天、地下联合开采的爆破震动安全评估[J].防冶工程,1985,59(1):6-11.
[4]于亚伦.爆破震动质点轨迹的分析[J].金属矿山,1981,7(6):25-36.
[5]张奇,高金石.爆破理论与爆破优化[M].西安:西安地图出版社,1993.
[6]言志信,工永和,江平,等.爆破地震测试及建筑结构安全标准研究[J].岩石力学与工程学报,2003,22(11): 543-545.
[7]卢文波,张乐,周俊汝,等.爆破震动频率衰减机制和衰减规律的理论分析[J].爆破,2013,24(22): 4158-4163.
[8]惠峰,李志龙,徐全军,等.减震孔对爆破地震波减震作用的数值模拟分析[J].爆破,2012,29(12),58-62.
[9]SUKUMAR N.The natural element method in solid mechanics[J].International Joumal for Numerical Methods in Engineering,1998,43:839-887.
[10]杨伟林,杨柏坡.爆破地震动效应的数值模拟分析[J].工程与工程震动,2005,25(1):8-13.
[11]SONG Bo,ZHONG Min,WANG Peifu.Optimization of monitoring the stability of surrounding rock in a metal mine[J].International Journal of Minerals,Metallurgy and Materials,2009,16(4):359-367.
[12]龙源,冯长根,徐全军,等.爆破地震波在岩石介质中传播特性与数值计算研究[J].工程爆破,2000,6(3): 1-7.
[责任编辑:韦 韬]
Monitoring and Attenuation Law of Blasting Vibration in Rock
LI Xiong-wei1,LI Xin-hang2
(College of Civil Engineering,Chongqing Jiaotong University,Chongqing 400074,China)
In order tostudy the propagation law of blast vibration waves in rock and damping holes,this paper,taking the rock blasting engineering surrounding the SK factory in Liangjiang New District, Chongqing,as example,using the ANSYS/Ls-dyna software and Sa Rodolfo J Ki’s empirical formula and through site tests,analyses the vibration velocity of ground particles before and after the shock absorption,and compares the results of the field tests with numerical simulation results.Results show: in the geological conditions of the local surrounding terrain,in the Sa Rodolfo J Ki’s empirical formula the Site coefficient(K)is 4 724.98 and the attenuation coefficient‘α’is 1.995 5;there are some differences between the field test results and numerical analysis,but the law of change is the same; and the cushioning effect of the double row dislocation damping holes is very obvious.
rock blasting;damping holes;particle vibration velocity;attenuation law
TD235.33
A
1006-7302(2016)03-0035-05
2016-04-25
李雄伟(1990—),男,四川资阳人,在读硕士生,研究方向为隧道开挖技术.
