双中心矩阵特征值反问题的最小二乘解

梁艳芳，袁仕芳（五邑大学 数学与计算科学学院，广东 江门 529020）

双中心矩阵特征值反问题的最小二乘解

梁艳芳，袁仕芳
（五邑大学 数学与计算科学学院，广东 江门 529020）

对于矩阵 A ∈ℝm× n，如果它的每一行元素之和等于零，且每一列元素之和也等于零，则称矩阵A为双中心矩阵.本文利用矩阵的列拉直算子、Moore-Penrose广义逆和一种矩阵向量积讨论n阶双中心矩阵特征值反问题的最小二乘解，得到了矩阵方程 AX =XΛ的双中心极小范数最小二乘解的表达形式.

双中心矩阵；最小二乘解；极小范数解；特征值反问题

本文把所有n维列向量组成的集合记为 ℝn，把所有m × n阶实矩阵所组成的集合记为 ℝm× n.对于矩阵 A ∈ℝm× n，如果A的每一行元素之和等于零，且它的每一列元素之和也等于零，则称矩阵A为双中心矩阵.把所有n阶双中心矩阵组成的集合记为DC ℝn× n.矩阵A的转置、共轭矩阵和Moore-Penrose广义逆分别记为 AT、和 A+.n阶单位矩阵记为 In.对于矩阵 A= （aij）∈ ℝn× n，它的迹为

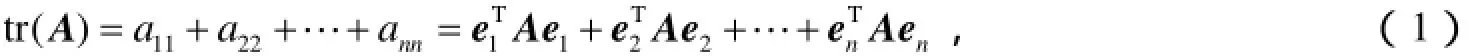
其中 ej表示n阶单位矩阵 In的第j列.对 A, B ∈ℝm× n，定义A与B的内积为A, B =tr(BTA)，则由此内积导出的范数是矩阵A的Frobenius范数，且 ℝm× n构成一个完备的内积空间，x2表示向量x的2范数.

矩阵的特征值反问题及其最小二乘解在科学和工程技术中有重要的应用，已取得了许多研究成果[1-3].我们在文献[4]定义的矩阵和向量积的基础上，讨论了双中心矩阵的特征值反问题的最小二乘解，并考虑如下问题：

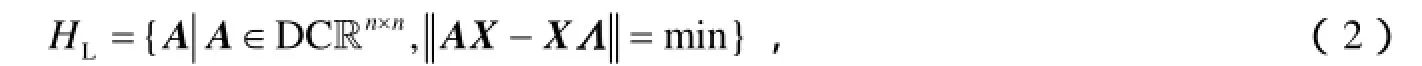
求 AD∈HL，使得

1 引理

为了讨论问题I，我们需要如下定义和引理.

定义1设 A =(aij)m× n，记 ai=(a1i,a2i,… ,ami)(i =1,2,… ,n)，令

定义2设 A=(aij)n ×n，记a1=(a11,a21,…,an-1,1)，a2=(a12,a22,a32,…,an-1,2)，…， an-1= （a1,n-1,a2,n- 1,…,a(n-1)(n-1)）.令

定义3[4]4982设 x=(x,x,…,x )T∈ℝk, y=(y,y ,…,y )T∈ℝk，以及 A =(A,A ,…,A)，其中12k 12k 12kA∈ℝm× n(i =1,2,… ,k )，令：1） A ⊙x=x A + x A +…+ x A ∈ℝm× n，2） A ⊙(x, y) =(A ⊙x, A ⊙y).易i1122kk知若 Ai∈ℝm，则 A ⊙x =Ax.

以下列出的是本文用到的文献[4]中的一些结论：

设B =(b, b ,… ,b )∈ ℝk× s， b∈ℝk(i =1,2,…,s)，C =(c, c ,… ,c )∈ ℝk× t， c∈ℝk(i =1,2,…,t)，12s i12t iD ∈ℝl× m，那么：

1） A⊙ B =(A ⊙b1, A ⊙b2,…,A ⊙bs)； 2） A ⊙(B, C )=(A ⊙B, A ⊙C)；

3） D( A ⊙x)=(D A)⊙x； 4） (A ⊙x) B =(A1B, A2B, …,AkB )⊙x.

假设 E ∈ℝs× m, F= (F, F,…,F )∈ ℝm× kn, F ∈ℝm× n(i= 1,2,…,k ),G ∈ℝn× s，那么：

12ki

5）E[( F1, F2,…,Fk) ⊙ x] G =(E F1G, EF2G ,…, EFkG )⊙x.

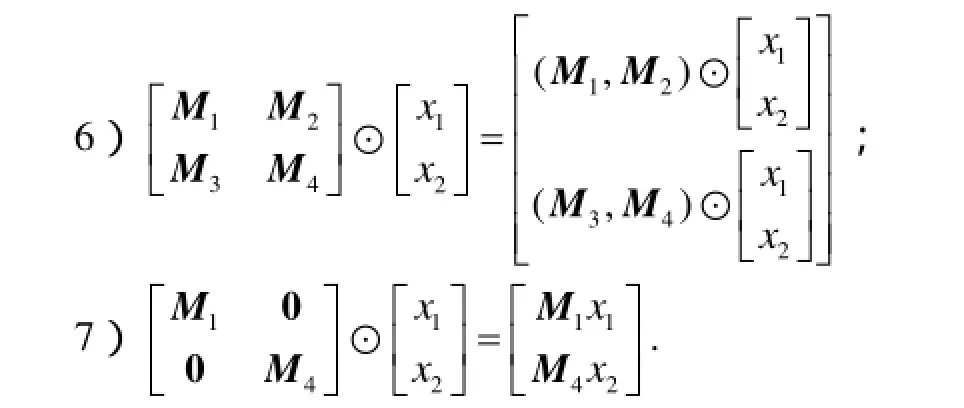
引理1[4]4980给定矩阵 A1, A2,… ,Al∈ℝm× n和 B ∈ℝm× n，求向量 k=(k1, k2,…,kl)T∈ℝl满足方程

如果矩阵方程（6）有解，则该解也是下列等式的解

引理2[4]4981给定矩阵 A1, A2,… ,Al∈ℝm× n和 B ∈ℝm× n，求向量 k=(k1, k2,…,kl)T∈ℝl满足

则式（8）的解集也是式（7）的解集.

设

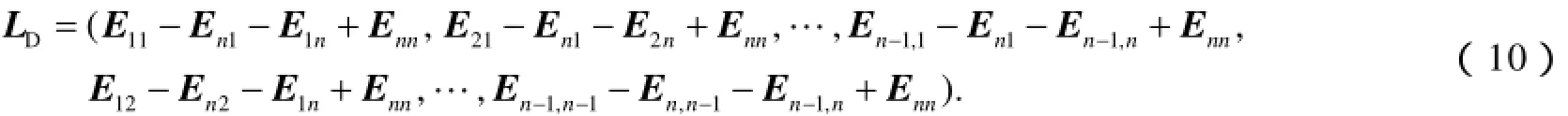
引理3 假设 A ∈ℝn× n，则有

引理4 给定矩阵 X ∈ℝn× n， A∈DCℝn× n，令 Xj是矩阵X的第j行向量， ei是单位矩阵 In的第i列向量， Eij如式（9）所示， vecD(A)如式（5）所示，则

1） EijX =eiXj；

2）令 Fij∈ℝn× n(i, j= 1,2,…,n-1)，其中 Fij=eiXj-enXj-eiXn+enXn，则有 AX =（F11, F21, …, Fn-1,1, F12,…,Fn-1,n- 1）⊙vecD(A).

引理5[5]i）给定 A ∈ℝm× n,b ∈ℝn，则线性方程组 Ax =b有解的充分必要条件是

在有解的条件下，它的通解是

其中 y ∈ℝn是任意向量.

ii）给定 A ∈ℝm× n,b ∈ℝn，那么不相容线性方程组 Ax =b的最小二乘解为

这里 y ∈ℝn是任意向量，并且它的极小范数最小二乘解为 x =A+b.

2 问题I的解

本节我们利用引理1～5给出问题I的解.给定矩阵 X∈ℝn× n， Λ=diag{λ1, λ2,… ,λn} ∈ℝn× n，记B =XΛ，令

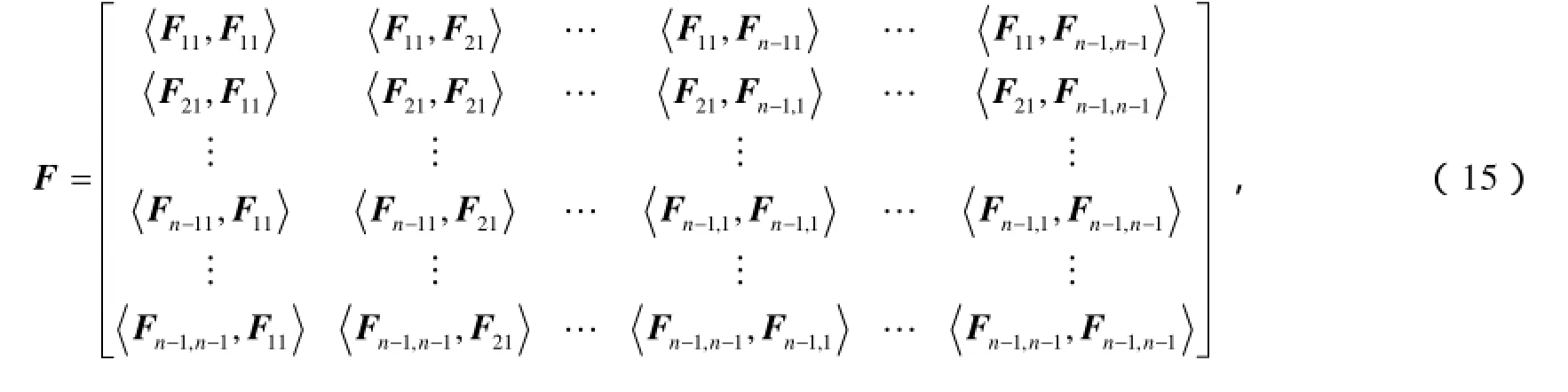
定理 给定矩阵 X=(x1, x2,… , xn)∈ ℝn× n， Λ= diag{λ1, λ2,… ,λn} ∈ℝn× n，其中 xi(i =1,2,…,n )∈ ℝn，LD如式（10）所示， vecD(A)如式（5）所示， F 、v分别如式（15）、式（16）所示.则问题I的解集 HL可表示为

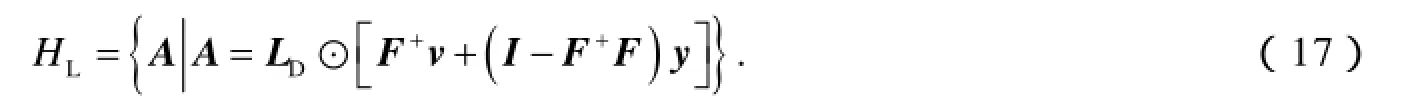
其中y为适当维数的任意向量.

进一步可得，问题I存在唯一的极小范数最小二乘解 AD∈HL，且 AD可表示为

证明 由引理3和引理4可得：

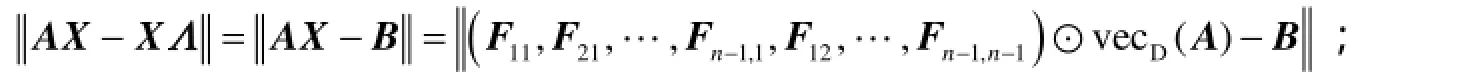
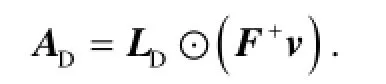
下面我们讨论形如

特征值反问题的解.

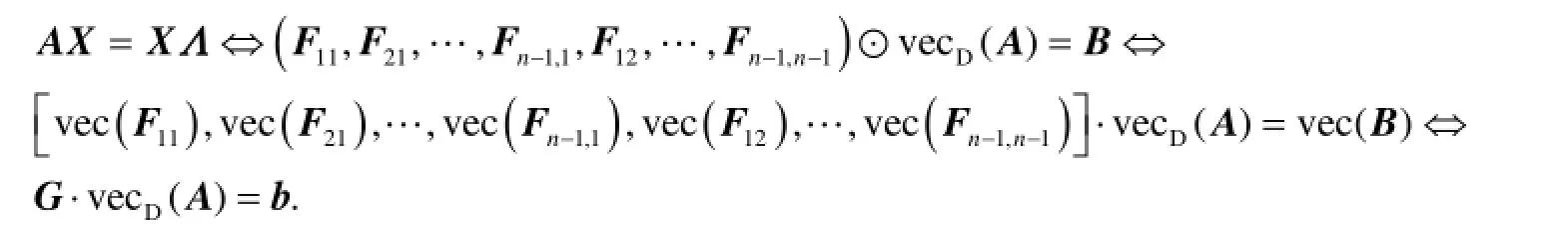
推论 矩阵方程（19）有解 A ∈DC ℝn× n的一个充分必要条件为

在有解的条件下，把方程（19）的解所组成的集合记为 HE，则其可表示为

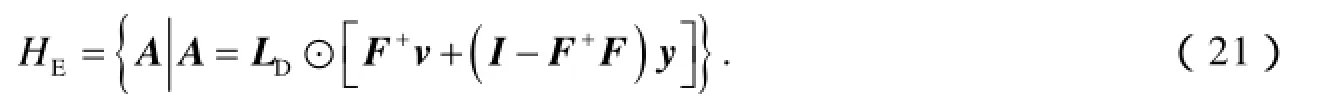
其中y是一个适当维数的任意向量.

进一步，如果等式（20）成立，那么矩阵方程（19）有唯一的解 A ∈HE的一个充分必要条件为rank(G) =(n-1)2.这时 HE可表示为：并且极小范数问题存在唯一解 AD∈HE，且 AD的表达式如式（18）所示.

[1]周树荃，戴华.代数特征值反问题[M].郑州：河南科学技术出版社，1991.

[2]孙继广.一类反特征值问题的最小二乘解[J].计算数学，1987,9(2):206-216.

[3]周硕，吴柏生.双中心矩阵反问题及其在电网络理论中的应用[J].工程数学学报，2007,24(4):611-617.

[4]YUAN Shifang,LIAO Anping.Leastsquares Hermitian solution ofthe complex matrix equation AXB + CYD = E with the least norm[J].Journal of the Franklin Institute,2014,351:4978–4997.

[5]戴华.矩阵论[M].北京：科学出版社，2001.

[责任编辑：熊玉涛]

Least Squares Solutions for the Inverse Problem of Double Center Matrix Eigenvalue

LIANG Yan-fang,YUAN Shi-fang
(School of Mathematics and Computational Science,Wuyi University,Jiangmen 529020,China)

For A ∈ℝm× n，if the sum of the elements in each row and the sum of the elements in each column are both equal to 0,then A is called a double center matrix.In this paper,we discuss the least squares solutions for the inverse eigenvalue problem of double center matrices with size n by using the vec-operator,the Moore-Penrose generalized inverse and a product of matrices and vectors.We also provide the expression of the least square double center solution with the least norm of the matrix equation AX =XΛ.

double center matrices;least-squares solutions;least norm solutions;inverse eigenvalue problems

O241.2

A

1006-7302（2016）03-0006-04

2016-03-07

广东省自然科学基金资助项目（2015A030313646）；江门市科技计划项目资助（江科〔2014〕145号）

梁艳芳（1991—），女，广东开平人，在读硕士生，主要从事矩阵方程数值解研究；袁仕芳，教授，博士，硕士生导师，通信作者，主要从事矩阵方程数值解研究.