基于MaxplusII的短时傅里叶变换实现研究

陈　军

(定西师范高等专科学校 物理与电子工程系，甘肃 定西 743000)



基于MaxplusII的短时傅里叶变换实现研究

陈军*

(定西师范高等专科学校 物理与电子工程系，甘肃 定西 743000)

文章对短时傅里叶变换(short-time Fourier transform，STFT)算法原理进行了研究分析，运用MaxplusII软件设计实现了快速短时傅里叶变换的可编程逻辑器件，详细地研究了基4蝶形处理单元的设计和旋转因子的地址生成规律，在满足时频率分辨率的条件下提高了运算速率、降低了运算度，并在高速率运行环境下达到了低频信号设计要求，节省了硬件资源。通过软件仿真研究分析，证明该设计的合理性。

现场可编程门阵列；短时傅里叶变换；实现；随机存取存储器

STFT因其有算法简捷、处理速度快及实现容易等优势而在低频信号分析、复合材料的损伤检测、钻柱等振动信号分析、图像信号处理等工程领域有广泛深入的应用[1-8]。对低频信号而言，通过短时傅里叶变换分析研究其窗口和帧偏移各不相同条件下的图像谱，所以要求STFT具有可调整的帧偏移，可灵活选择的窗类型，可变化的窗口长度。对信号进行短时傅立叶变换，目的是对不同时刻和频率相对应的能量密度或强度等信号特征参量的线性时频分析。

STFT是和傅里叶变换相关的一种数学变换，用以确定时变信号在其局部波形区域内相位、频率等的参量。也就是在进行信号分帧处理之后采用快速傅里叶变换进行的计算。其思想为先选择一个时频局部化的窗函数，假定分析窗函数在一个短时间间隔内平稳，移动窗函数，使两者的积在不同的有限时间宽度内平稳，从而计算出每个不同时刻的功率谱。STFT使用的窗函数确定之后，其分辨率也就确定了。若要改变分辨率，则需要重新选择窗函数。对于波形变化比较平缓的低频语音信号，需要窗函数具有较高的频率分辨率。STFT窗函数满足海森堡不确定原理，即窗函数的时间与频率分辨率不能同时达到最优。STFT中基2算法和基4算法具有类似性，但相比较基4算法控制较为复杂，分裂基算法的计算速度最好，但是操作不易，控制相难度较大。运用基4蝶形处理单元与多输入多输出存储器结合来并行流水处理数据，提高数据处理速度[3-9]。

MaxplusII以其易使用的图形界面，具有高密度、高速度、现场模拟调试验证性强、逻辑实现能力强、设计灵活，在最短的时间，以最少的精力，达到最优的硬件设计，空间的并行性运算和时间上可流水线性处理的特点，在数字音频、图像信号处理领域得到广泛使用[4-14]。本文通过对短时傅里叶变换算法原理研究，运用MaxplusII仿真设计了实现快速短时傅里叶变换的可编程逻辑器件。详细地研究了基4蝶形处理单元的设计和旋转因子的地址生成规律，对设计要求运用该软件进行了分析讨论。

1　短时傅里叶变换的数学模型

STFT是对信号分帧处理之后采用快速傅里叶变换进行的计算。先选择一个时频局部化的窗函数，其窗函数的时宽足够窄，在分析窗口对应的短时间间隔内信号足以平稳，沿时间轴移动窗函数，使两者的积在不同的有限时间宽度内平稳，从而计算出信号在每个不同时刻的功率谱数学表达式。对于时间信号x(t)，其STFT的数学模型[12-15]：

(1)

该式中，h(t)是窗口函数， 短时傅里叶变换的局域特性是通过窗函数的时间移位和频率移位实现的。对于一定时刻t，X(f，t)同时表现出时间函数和频率函数双重性，看成是对应时刻的局部频谱，故利用这些特点将信号作时域和频域的研究分析。

2　基于FPGA的 STFT实现设计

基4-STFT实现框图如图1所示，是由快速傅里叶变换(Fast Fourier Transformation，FFT)算法的实现和对信号进行FFT运算前的分帧及加窗两部分实现来完成[3，8，13，14]。

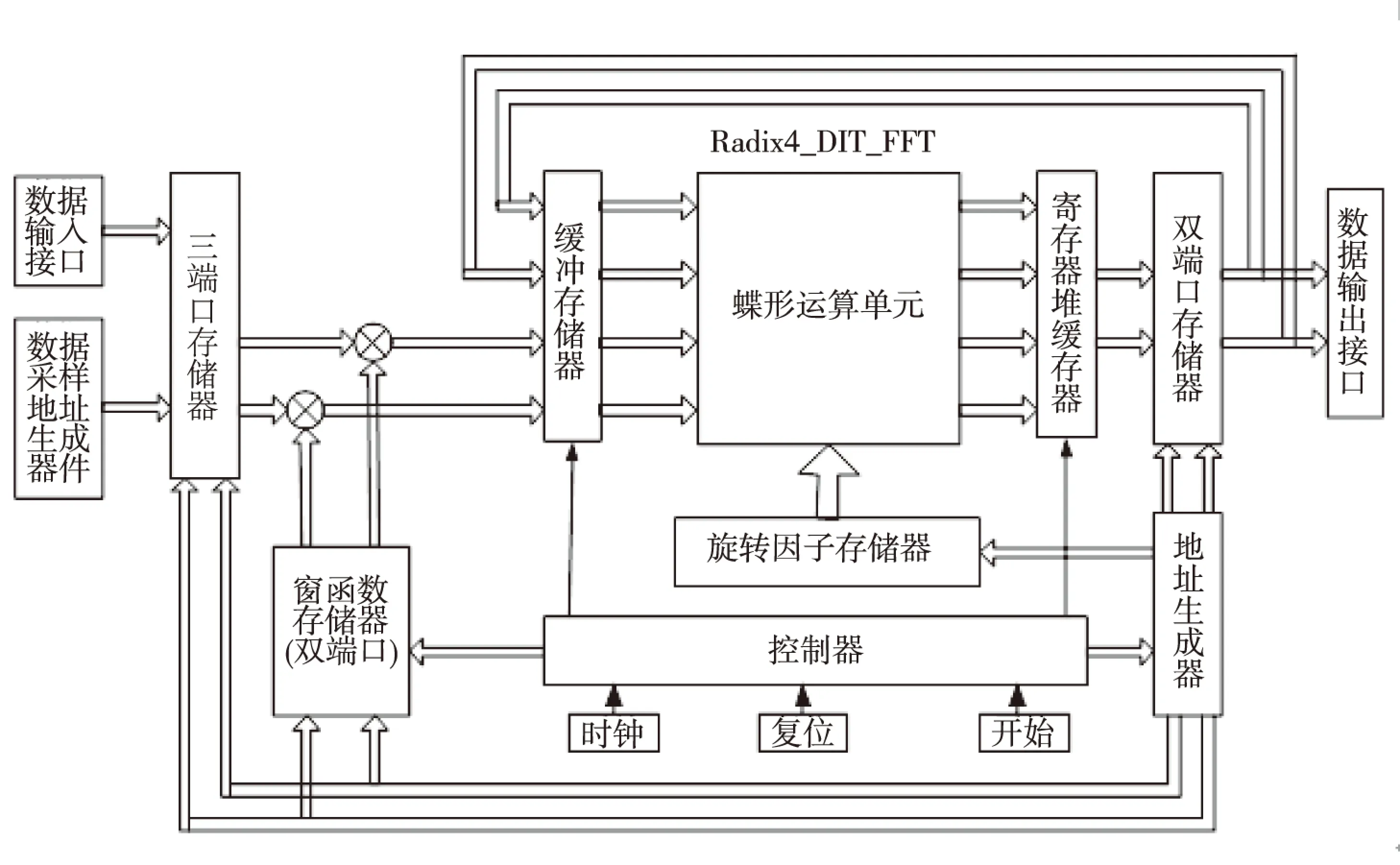
图1　基4-STFT实现框图

STFT实现的过程框图中，三端口随机存取存储器中的数据准备就绪之后，启动FFT运算单元，三端口随机存取存储器中的数据被读取，窗函数只读存储器中的数据也被同时读取而加窗运算，才被分时送进蝶形运算电路，与此对应，地址单元也产生旋转因子查表地址，相应地蝶形运算处理器从旋转因子存储器中读取其值，将处理后的结果原址暂时存放在寄存器堆缓存器中，随后存入FFT运算单元配置的双口随机存取存储器中，以供下级数据处理器使用。

基4蝶形运算单元设计是调用内部硬件乘法器构造复数乘法器，运用两级流水线，并行处理4路输入数据的工作方式来提高处理速率。产生旋转因子查找表地址的方式是先计算出旋转因子，然后存储到旋转因子存储器中以便使用。不同级运算读取随机存取器RAM的地址时，旋转因子的查寻找的地址不相同，但具有一定的规律。基4算法的地址产生规律中每个蝶形运算单元需要4个输入数据，在不同的级上有不同的数据寻址规律。

本系统共设计了六级运算模块，每级都配置有一个双口随机存取存储器，一个地址产生器，一个旋转因子产生器和一个蝶形运算单元。当FFT中第一级运算单元开始工作时，从双口随机存取存储器中读取的数据经蝶形运算后，原址存进下一级存储单元。为了确保第一级蝶形运算结果准确地存储到第二级处理单元的存储器中，此时相邻的后级及其后各级均为等待状态。当第二级开始计算时，它的前级即第一级停止运算，其后级同样处于等待状态。当第三级开始计算时，第四级及其后级还未开始计算，第一级又开始工作，第二级停止计算。按此方式依次类推，当第一帧数据计算完成后，后续数据进入流水处理。依次运行六级计算处理后，到FFT运算结果。

2.1信号分帧加窗实现设计

为了处理语音信号，我们要对语音信号进行加窗，也就是一次仅处理窗中的数据。因为实际的语音信号是很长的，我们不能对非常长的数据进行一次性处理。解决办法就是每次取一段数据，进行分析，然后再取下一段数据，再进行分析。

对汉明窗中的数据进行FFT运算，一个窗内的信号表现出一个周期的信号。实际上一段音频数据没有明显的周期性，加上汉明窗后，数据形状就明显具有了周期性。因加上汉宁窗，只有中间的数据体现出来了，两边的数据信息丢失了，所以每次移窗函数时，移动1/3到1/2窗长度，这样被前一帧丢失的数据又重新得到了补偿。

三端口RAM可以在FPGA内部定制，主要有一个写地址端口和数据写入端口，两个读地址端口和数据输出端口，其最大优势为同时进行写入和读出，并且具有不同速率的写入和读出数据的功能，可应用于环形存储器。对于写入数据，其速率为低频信号的采样率，而读取数据的速率是FFT处理单元的时钟速率。

2.2数据地址产生规律

该设计采用计数器的方式获得读取数据地址。设蝶形处理单元中基本地址ad，也就是蝶形运算单元中的第一个数据的地址ad1。对于1024点按时间抽取的基4-FFT算法共有5级，其数据地址规律如表1所列。

表1　蝶形单元数据地址规律

2.3旋转因子存储器实现设计

本设计采用查找表方法，利用旋转因子的对称性，建立了一个共有N/4组旋转因子的存储表。设x(n)为N=4L点有限长序列，L为整数，则N点离散傅里叶变换(DFT)定义为[15-16]：

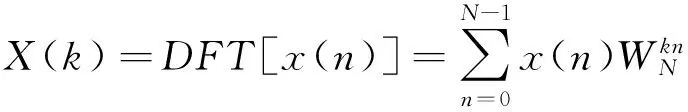
k=0，1，…，N-1

(2)

按时间抽取，对DFT进行基4算法分解，写出第m级递推公式为：

Xm(k0，k1，km-1，nL-m-1，···，n1，n0)

(3)

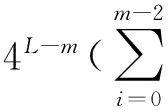
(4)

2.4蝶形运算单元的实现设计

蝶形运算是快速傅立叶变换(FFT)中最基本的一个运算单元。在FFT程序设计中要找到蝶形运算地址与第几级迭代，第几组之间的关系。在第m级，有如下关系：

(5)

式中，m为第级数，p、q分别为单元地址，p-q=2m。

3　实验仿真分析

针对本文提出的短时傅里叶变换结构采用Spartan-IIE系列XC2S200器件进行了验证。图2利用仿真软件[17]逻辑综合、布局布线、时序仿真和硬件实时在线仿真测试，设置低频信号采样频率为32 kHz，选取分析窗函数为海明窗函数类型数据点进行加窗，图中显示了在某一时刻，捕获的STFT低频信号的幅度谱波形。主瓣加宽，旁瓣显著减小，与理论计算波形相符合。

4　结束语

结合语音信号时频处理的实际需要，通过对STFT算法的分析研究，借助于仿真平台设计实现快速的短时傅里叶变换的可编程逻辑器件。详细地研究了基4蝶形处理单元的设计和旋转因子的地址生成规律，在满足时频率分辨率的条件下提高了运算速率、降低了运算度，并在高速率运行环境下达到了低频信号设计要求，节省了硬件资源。最后，进行了仿真研究分析，达到信号处理的设计标准。

图2　嵌入式逻辑分析仪显示仿真图

[1] 金朝娣，能昌信，王振翀，等.基于STFT填埋场衬层修补技术中振动信号分析[J].计算机仿真，2011，28(7):277-280.

[2] 夏明赟，蒋涛.一种基于FPGA的高速短时傅里叶实现[J].通信技术，2012，45(7):113-115.

[3] 陶中幸.基于FPGA的信号时频分析方法研究[D].兰州：西北师范大学，2012.

[4] 杨小娜，黄欢，徐晓煜，等. 基于小波模极大值多尺度的图像边缘提取[J].贵州大学学报(自然科学版)，2013，01:91-93.

[5] 晏勇.基于FPGA三相正弦信号发生器的设计与实现[J].电气自动化，2014，36(4):38-40.

[6] 陈军.基于FPGA的FFT变换分析与电路设计实现[J].工业仪表与自动化装置，2016(1):40-42.

[7] 刘美容.FFT算法的DSP实现[J].微电子学与计算机，2015，32(1):76-79，84.

[8] 陈军.基于MaxplusⅡ的短时傅里叶变换分析及仿真实现研究[J].辽宁大学学报(自然科学版)，2016，43(1):27-31.

[9] 李允公，姚兆，刘杰，等.基于瞬时频率的窗宽递增寻优的短时傅里叶变换[J].东北大学学报(自然科学版)，2007， 28(12):1737-1740.

[10]赵海臣，李良荣，李丛飞.FFT与IFFT频域信号处理研究[J].贵州大学学报(自然科学版)，2014，31(2):64-68.

[11]孙红英，杨鸿武，陶中幸.语谱分析的FPGA实现[J].电子与信息学报，2011，33(5):1238-1242.

[12]杨鑫，章红平，张提升.基于FPGA的快速捕星方法实现[J].武汉大学学报(工学版)，2015，48(3):424-428.

[13]王全州，裴东，杨志民，等.基于FPGA的FFT处理器的研究与设计[J].西北师范大学学报(自然科学版)，2008，44(5):38-42.

[14]段小东，顾立志.高性能基4快速傅里叶变换处理器的设计[J].计算机工程，2008，34(24) : 238-243.

[15](美)罗纳德 N 布雷斯韦尔.傅里叶变换及其应用[M].殷勤业， 张建国， 译.西安:西安交通大学出版社， 2005:217-225.

[16]程佩青.数字信号处理教程[M].3版.北京：清华大学出版社，2007:202-326.

[17]王钿，卓兴旺.基于verilog 的数字系统应用设计[M].2版.北京： 国防工业出版社，2007:208-234．

(责任编辑：曾晶)

Implementary Study of Short-time Fourier Transform Based on MaxplusII

CHEN Jun*

(Department of Physics and Electronic Engineering， Dingxi Teachers’ College， Dingxi 743000， China )

The programmable logic devices of the short-time Fourier transform of fast speed was designed and realized through the principle analysis and study of short time Fourier transform algorithm using MaxplusII. The base 4 butterfly processing unit design and rotation factor address generation rule was studied. It improves the operation rate， reduces the operation under the condition of meeting the frequency resolution， and it attains the design requirements of the low frequency signal in the high speed running environment， saves hardware resources. It proves the rationality of the design through software simulation analysis.

FPGA; STFT; implementation；RAM

A

2016-02-20基金项目： 国家自然科学基金项目(60971294);定西师范高等专科学校项目(DS1505)

陈军(1969-)，男，教授，博士，研究方向：信号与信息处理，Email: chenjun5582@163.com.

陈军，Email：chenjun5582@163.com.

TN911.7