Young不等式及其应用

薛建明，周　旋

(昆明理工大学 津桥学院，云南 昆明 650106)



Young不等式及其应用

薛建明*，周旋

(昆明理工大学 津桥学院，云南 昆明 650106)

Young 不等式是一个非常重要的不等式，它在分析数学中有着广泛的应用，对促进现代数学的发展起到了非常重要的作用。本文利用Young 不等式证明了Hölder不等式和Young 逆不等式，进而证明了Bernoulli不等式。

Young 不等式; Hölder不等式; Bernoulli不等式

(1)

文献[2]证明了对于任意的a，b>0，0≤v≤1，有

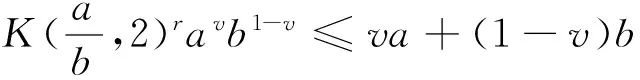
(2)

本文将利用推广的Young 不等式证明Hölder不等式，Young 逆不等式和Bernoulli不等式。

1　主要结果

定理1(Hölder不等式) 对任意的ai，bi>0，

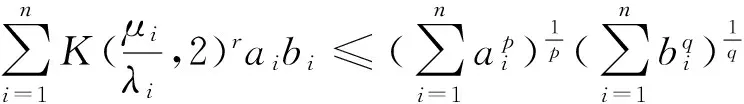
i=1，2，…，n。

由(2)式可知

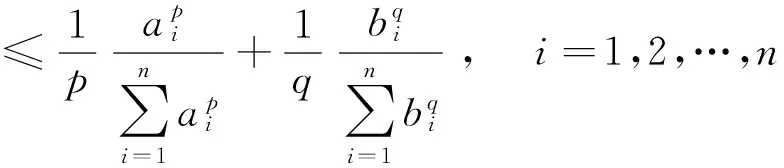
对i=1，2，…，n求和得

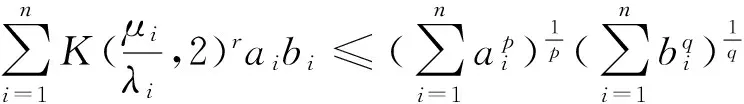
定理2(Young 逆不等式) 对任意的a，b>0，

0

r=min{p，1-p}。

(3)

定理3(Bernoulli不等式) 对任意的x>0，当

0<α<1时，

K(x，2)rxα-1≤α(x-1)，r=min{α，1-α};

当α>1时，K(xα，2)-rxα-1≥α(x-1)，

K(x，2)rxα≤αx+(1-α)，r=min{α，1-α}，

即K(x，2)rxα-1≤α(x-1)。

即K(xα，2)-rxα-1≥α(x-1)。

K(xα-1，2)-rxα≥αx+(1-α)，

即K(xα-1，2)-rxα-1≥α(x-1)。证毕。

[1] 胡克. 解析不等式的若干问题[M]. 武汉: 武汉大学出版社， 2006.

[2] Zuo H， Shi G， Fujii M.Refined Young inequality with Kantorovich constant.[J]J Math Inequal， 2011，5(4):551-556.

[3] F Kittaneh. Y. Manasrah， Improved Young and Heinz inequalities for matrices[J].J Math Anal Appl，2010，361:262-269.

[4] T. Ando. Matrix Young inequality[J]. Oper Theory Adv Appl，1995，75:33-38.

[5] 胡兴凯.矩阵的Young型不等式[J].华东师范大学学报(自然科学版)，2012(4)：12-17.

(责任编辑：曾晶)

Young Inequality and its Applications

XUE Jianming*，ZHOU Xuan

(Oxbridge College， Kunming University of Science and Technology， Kunming 650106， China)

Young inequality is an important inequality which is used widely in mathematical analysis and plays an important role in the development of modern mathematics. The proofs of Hölder inequality and reverse Young inequality by Young inequality were presented．Then the proof of Bernoulli inequality was given．

Young inequality; Hölder inequality; Bernoulli inequality

A

1000-5269(2016)03-0008-02

10.15958/j.cnki.gdxbzrb.2016.03.03

2014-12-19

云南省教育厅科学研究基金资助项目(2013Y082)

薛建明(1982-)，女，讲师， 研究方向：泛函分析与矩阵理论，Email：xuejianming104@103.com.

薛建明，Email：xuejianming104@163.com.

O178