B-S期权模型在可转债定价中的应用
——考虑违约风险与附加条款的引入
2016-08-16
(武汉大学经济与管理学院 湖北 武汉 430072)
B-S期权模型在可转债定价中的应用
——考虑违约风险与附加条款的引入
陈垚翰
(武汉大学经济与管理学院湖北武汉430072)
可转换债券是指发行人依照法定程序发行,赋予其持有人在一定时间内依据相关约定条件将其转换成一定数量股票的公司债券。20世纪70年代中期以后,Black.F.和M.Scholes以及Merton等人对期权定价的研究工作极大推动了可转换债券的定价研究,可以说可转换债券定价的现代研究是在将可转换债券中的转股或有权益视为某种期权的基础上进行的。本文将基于B-S期权模型以及与之相关的数学工具和思想方法对可转债的定价问题进行研究,在考虑公司价值度量问题的基础上考虑发行公司的违约风险,基于欧式期权给出可转债定价公式。并进一步考虑该公式在可转债定价中的应用和推广——在可转换债券中引入赎回与回售条款,直接基于期权定价中的B-S微分方程,通过求解带有初边值条件的B-S微分方程给出可转换债券的定价公式。
可转换债券定价;期权模型;B-S方程;附加条款
一、引言
可转换债券是兼有股票和债券性质的结构化产品,赋予债券持有人在规定的时间内以特定的价格转换成股票的权利。作为固定收益类证券,它具有确定的债券期限和利息率,使得投资者可以获得固定的利息收入;同时,转股或有权益的存在使得可转债的持有人可以按照约定的条件将可转换债券转换成相应的股票,充分分享发行人业绩增长和股价增长的潜力。另一方面,作为资本市场一种主要的融资工具,可转债对发行人而言具有明显的低成本优势,并且由于它具有融资规模大、操作灵活、对发行公司业绩压力较轻等特点,同时可以对相关股票的发行提供相应的稳定机制,因此正逐渐受到许多公司的青睐,成为我国资本市场不可或缺的重要组成部分。
作为一种复杂的信用衍生产品,可转债定价的复杂性表现在除了债券之外,转股或有权益以及相应的条款使得它还包含着一系列的期权,要对可转债进行定价,就必须在合理的假设基础上结合具体的市场实际情形,适当地拆分期权,选择合适的期权定价模型和方法。尤其对于中国的可转债市场,由于起步晚同时存在着较为严格的监管机制,如何找到适应于这种现实市场情形的可转债定价模型对学界研究的要求显得尤为迫切,因此这也是本文将要讨论的重点。
传统上,Ingersoll、Nyborg、Brennan、Schwartz等人在Merton的结构化模型的基础上发展的可转换债券定价模型,在分析讨论问题时往往是以公司价值作为标的资产,将可转换债券看成是基于公司价值的衍生证券。但是这种处理已经为一些学者指出,在实际操作中难以对公司的价值直接进行度量。本文也将基于股票价格对可转换债券的定价进行研究,但是将对这种处理的合理性进行相应的讨论,并且将发行公司的违约风险作为期权进行处理,基于欧式期权定价模型给出一个可转换债券的定价公式。
在实际可转债交易中往往存在相应的条款,作为一种商业契约,这些条款是发行人向投资者的具有法律效力的约定,其中可赎回与可回售是可转债交易中最基本也是普遍存在的条款。这实际上是赋予了发行公司和投资者相应的期权,并且这种内嵌期权往往与债券不可分割,增加了对可转换债券定价的难度。本文将在一定的假设条件下,基于期权定价中的对冲思想构造投资组合,从B-S方程入手,通过求解带有边界和初值条件的B-S方程给出可转债的定价公式。最后在理论分析的基础上,结合我国的可转债市场进行实证分析,通过比较可转债理论价值与实际价值之间的差异,分析存在差异的原因,为相应的可转债定价提供理论参考。
本文的整体研究思路是基于期权模型对可转换债券进行定价,具体来说在思路层面上是从两个方面着手的:一方面将可转换债券中的或有权益看成相应的期权,借助已有的期权定价公式对可转换债券中的或有权益进行定价,进而对可转换债券进行定价;另一方面,针对附有附加条款的可转换债券,本文将放松一些基本假定,直接从期权定价模型推导B-S方程的方法入手,将可转换债券的价值视为以相关股票价格为自变量的收益函数,通过建立和求解相应的PDE对可转债进行定价。
二、文献综述
B-S期权模型自上个世纪70年代由Black.F.和M.Scholes等人提出后,直接利用该模型的结论或者利用B-S模型无风险套利的分析方法进行的研究对金融领域其他方向研究的发展起到了巨大的推动作用。Merton(1974)在此基础上又进一步讨论了公司债券的定价问题,这些都为后续基于B-S模型对公司债券、可转换债券以及其他衍生产品的定价的研究打下了基础。上个世纪九十年代,KMV公司基于Merton的资产价值理论,将债权看作债权人向借款公司股东出售的对公司价值的看跌期权,并假设信用风险由债务人资产价值驱动,在此基础上开发的KMV(EDF)模型已经成为信用风险度量领域的经典模型。同时,实物期权概念的引入使得金融期权的相应理论(比如B-S期权模型)在投资决策、公司的筹融资策略、财务分析和并购等方面得到了广泛的应用。在[3]的研究中,对于公司的投资决策所产生的投资扩张价值的估计,将未来的投资机会视为一种买权,以B-S期权模型的方法计算买权的价值,再将买权的价值加总作为投资的扩张价值。对于公司的并购,[3]的处理方法是将公司的无形资产看作是一种买权,公司有形资产的价值是其约定价格,相应的公司未来现金流的总现值则是其标的物的当前价值,将公司的并购看作是一个可以取得未来现金流的买权,通过计算该买权的价值来估计公司并购的价值。此外,周鹏(2007)在基于B-S方程的基础上,通过求解一个倒像半无界的线性抛物型偏微分方程对标准的信用违约互换进行了定价。梁进和孔亮亮考察了券商集合理财产品中以风险投资组合为对象的非限定性集合资产管理计划,基于B-S期权模型的研究框架,分别考虑了固定封闭期含隐形保本条款情形下和有封闭期的特殊条款的情形下该理财产品定价的封闭解。
概括来说,利用期权模型研究相应的经济问题的核心思想是将某种或有选择权视为一种期权,再利用期权定价的方法和无风险套利的思想对或有期权进行定价,进而研究相关的经济问题。
早期的可转债定价研究基本上是指在20世纪70年代中期以前对可转换债券基本概念以及相应的价格确定与调整方面的研究。最早对可转换债券进行理论上定价的尝试可以追溯到20世纪60年代,这一时期的研究思路大致上是将可转换债券作为纯债券的最大值或者未来某一时点转股后的权益价值进行贴现作为可转换债券的价值(Poensgen 1965;Baumol et al.1966;Weil et al.1968;Walter and Que1973;Jennings 1974)。但是,这些研究大都囿于理论方法与研究工具的限制。无法准确地刻画可转换债券债性与股性的双重属性以及相应的价值。并且一些基本的难点(比如可转换债券中存在的或有权益的定价)并没有得到解决。
20世纪70年代中期以后,Black.F.和M.Scholes以及Merton等人的工作对期权定价理论的发展起到了革命性的作用(Black.F.和M.Scholes,1973)。在此基础上,Ingersoll和Brennan等人基于或有权益的视角,以公司价值作为标的资产并且假设其服从几何Brown运动,在Merton提出的结构化模型的基础上对可转债的定价进行了相应的研究。(Ingersoll J.1977a和Ingersoll J.1977b以及Brennan和Schwatz,1977)。自此以后,关于可转换债券的定价研究在一段时间内基本上是在这一框架结构下进行的,然而,公司价值在现实中往往难以直接度量,因此直接基于公司价值的可转债定价模型往往缺少实用价值。为了解决这一问题,MaConnell和Schwartz(1986)等人提出了一个以相关股票价格为标的随机变量的关于零息债券的单因素可转换债券定价模型。
然而作为一种混合金融工具,可转换债券的定价难点是多方面的。首先,可转换债券的价值依赖多个变量,包括相关股票的价格(这种价格机制是动态的),利率以及发行人的信用风险以及这些变量之间的相互作用。其次,可转换债券附有多种内嵌期权,这些内嵌期权与债券本身紧密相连,并且往往不是严格意义上的到期行权,在某一时间内表现出很强的路径依赖性(Path Independent)。这些特性都增加了可转换债券定价的难度,也促进了可转换债券定价的深入研究。在Ingersoll等人的工作基础上,Lewis(1991)在考虑了更复杂的资本结构的假设条件下,给出了一个可转债的定价公式。Takeakikariya和Hiroshitsuda(2000)基于连续时间的Markov模型利用传统的B-S公式提出了新的可转换债券的定价模型,Song-Ping Zhu和Jing Zhang(2010)通过对可转换债券进行新的期权拆分提出了有溢价形式的可转换债券的定价公式。Jun-Feng Qiu和Yong-Li Zhang(2013)基于随机分析在考略了转股价格可调整后对可转换债券的定价给出了闭形式的解。
尽管对可转债定价闭形式的解的研究进展很快,但是这总要在较为理想的假设条件下进行相应的推导,因此总会与实际情形有所出入,在这样的背景下,利用数值与仿真的方法对可转换债券进行定价正逐渐引起学界的关注。其中数值的方法仍然是以求解PDE为基础的,只不过对于一些难以解析求解的PDE采用有限元和有限差分等方法进行数值求解。这种方法由于简化了许多假设条件使得建立的PDE往往比较复杂,因此从某种意义上来说,数值方法也是唯一的选择。Bardhan et al.(1993)、Tsiveriotis和Fernandes(1998)将可转换债券的价值拆分为股票价值和纯债券价值部分,并分别用无风险利率和市场风险利率对股票价值和纯债券价值进行贴现,通过建立相应的PDE对可转换债券进行定价。Ammann et al.(2003)在考虑了多种买权触发条件的情形拓展并延伸了这种方法,Hung和Wang(2002)[15]又在此基础上基于树模型,提出了同时考虑随机利率和违约风险的可转债定价模型。
本文将首先考虑零息债券同时引入可赎回与可回售条款,在理论上给出级数形式解的基础上,通过数值求解一个算例说明对可转换债券的价值特性。在此基础上针对中国当前可转债市场鲜有回售交易的实际情况,只考虑赎回情形的可转债定价,给出一个相对简洁并且能够解析求解并能编程实现的定价公式。
三、基于欧式期权B-S公式的可转债解析定价
(一)公司价值的度量
基于期权模型对可转换债券进行定价必须选择合适的标的资产,传统上Ingersoll、Nyborg、Brennan、Schwartz等人的工作是在Merton的结构化模型的基础上直接以公司价值作为标的资产,将可转换债券看成是基于公司价值的衍生证券,然而这就涉及到如何度量公司价值的问题。现实中,发行公司的股票价格数据是容易获得的,一个很自然的想法(并且现有的许多研究也是这样进行的)是将可转换债券的转股或有权益部分视为基于公司股票价格的衍生工具,这样便可以对可转换债券的或有权益部分进行定价,但这样处理就必须对相应的合理性做一些讨论。
事实上,如果假设发行公司的资本结构仅有权益与债务构成,并且所有的债务均具有可转换性,那么将可转换债券的权益部分视为基于公司价值的衍生证券与将可转换债券的权益部分视为基于公司股票价格的衍生证券的处理方式是一致的。在该假设的基础上,设t时刻发行公司的股票价值和股票的价格分别为At和St,债券面值为M,发行数量为n,市场已经流通的股份为m,则有
mSt+nM=At
(2.1)
进一步假设St服从几何Brown运动
dSt=uStdt+σStdWt
(2.2)
其中μ,σ为常数,Wt为标准的Brown运动。考虑到
dAt=d(At-nM)=mdSt=mSt(μdt+σdWt)
(2.3)
所以公司价值的波动性实际来源于股票价格的波动性,如果如果进一步做简单的数学处理
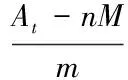
(2.4)
由(3.6)可以认为公司价值可以近似的视为几何Brown运动,不同的是多了nM的平移量。从某种意义上来说,这从标的资产波动性的角度说明了以股票价格代替公司价值的合理性,而以上两种处理方式的一致性可以从以下转股或有权益执行边界的角度加以说明。
假设可转换债券的到期日T,到期方可转股,股票的价格在T时刻的价格为ST,相应的转股价格为Pb,考虑到转股股份增加造成的摊薄效应,转股后的股票价格应该发生变化,记为Sa,则有

(2.5)
当债券到期时,持有人累计应得利息支付以无风险利率在T时刻的现值为KT,若以公司价值为标的资产,公司不对所持债务违约的必要条件为公司价值大于T时刻所持债务的现值,即
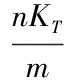
(2.6)
相应的,可转换债券持有人执行或有权益的边界条件为

(2.7)
(3.8)与(3.9)说明从期权执行边界的角度,在一定的假设条件下,以股票作为标的资产与以公司价值作为标的资产是一致的。
然而需要说明的是,上述所有推导的一个基本假设前提是除了权益与可转换债务,发行公司其他形式的资本所占比例很小,这需要结合具体的可转债,分析相应的发行公司的资本结构是否适合该模型的假设,这一点将在实证分析部分进一步说明。
(二)可转换债券的基本价值构成与权益属性
作为一种特殊公司债券,是发行人与投资者之间的一种契约,可以近似拆分为债券部分与股票部分。首先,可转债体现为债性,发行人必须每年固定地付给投资人利息。以及到期还本付息;其次,可转债体现为股性,持有人有权按事先契约规定的转股价格对应的转换比例,把相应的可转换债券转换成一定数量的股票,相应的转换价值就是直接转换成股票的价值:
转换价值=股票时价×转换比例
显然可转换债券作为债券的价值可以以一无风险利率对其到期收益贴现得到;而相应的转换价值则依赖于转股时的股票价格,并且理性的投资者只会在到期日股票价格大于执行边界条件时才会转股,因此可以将投资者的转股或有权益视为投资者持有的对可转换债券相关股票价格的看涨期权,从而以欧式期权定价公式对可转债的或有权益价值定价。由(2.7)可知执行可转债的或有权益的边界条件为ST>Pb,相应的收益函数为
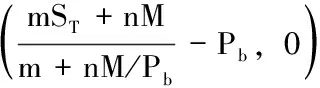
(2.8)
由收益函数闭形式解的一般形式可知,可转换债券转股或有权益的价值为
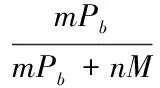
(2.9)
其中c(Pb,T;St)为执行价格为Pb,期限为为T的欧式看涨期权的价值。
作为债券就存在相应的违约风险,该如何刻画发行公司的违约风险的价值?由(2.6)发行公司不违约的必要条件可知,一旦公司违约,债券持有人的损失为
max(nKT-mST)
(2.10)
若债券持有人平均分摊损失,则对于单位证券,相应的损失为
(2.11)
因此发行公司债券的违约风险可以近似的用发行公司持有的基于公司股票价格的看跌期权来刻画,同样由收益函数函数闭形式解的一般形式可知,发行公司违约风险的价值为
(2.12)
其中,
至此,可以将以上的分析总结为:在一种较为理想的条件下,如果做出以下假设。
(1)可转换债券的价值由纯债价值与转化价值构成。
(2)纯债价值可以以一无风险利率对其到期收益贴现。
(3)可转债持有人到期转股,转换价值可以看成可转债持有人持有的基于公司股票价格的看涨期权。
(4)纯债价值中考虑公司违约风险,违约风险可以看成公司基于公司股票价格对可转债持有人的看跌期权。对可转债持有人而言,可转换债券的债性价值为纯债价值减去发行公司的违约风险价值。
那么可以得到可转换债券价格的一个理论表达式:

为了结合这个定价公式对可转换债券的价值属性进行相应的分析,本文以以下算例进行简要的说明:
假设发行可转债的份数为n=72000000,流通的股份数为m=870000000,转股价格为Pb=4.2,无风险利率依次取为0.026、0.027、0.028(按连续复利计算),债券的面值为100,剩余期限为3年,股票的价格在4-4.5之间,股价波动率为σ=0.1。通过MATLAB可以分别绘制出相应的可转债价格与股票价格的关系:
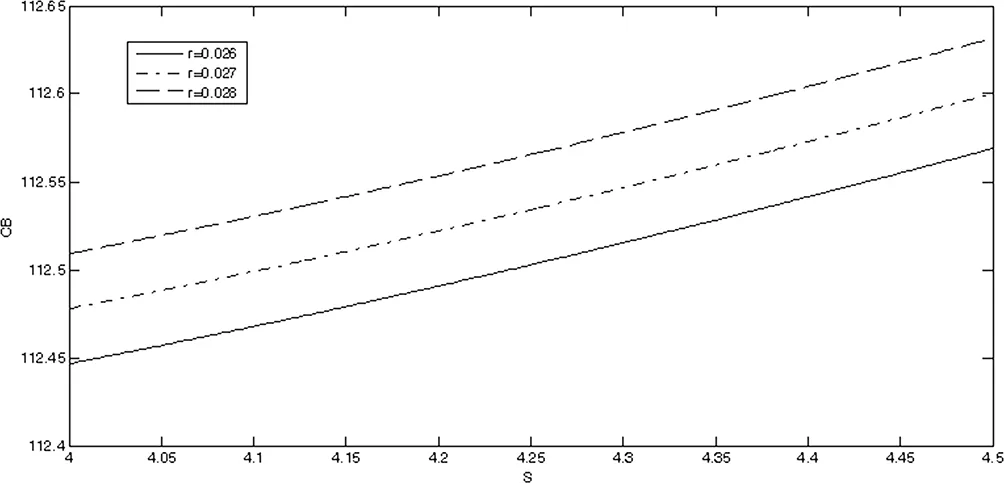
图2-1 可转债价格与股票价格的关系
由上图可知,可转换债券的价格随股票价格的增加而增加,并且无风险利率越高,相应的可转换债券的价格越高,这与直观上的认识是相符合的。
四、引入附加条款的可转债B-S期权模型定价
(一)同时引入可赎回与可回购条款的可转债定价
将发行公司的可转换债券的价值记为V,V是关于股票价格St和时间t的函数,记为V(S,t)。假设公司的股票价格满足几何Brown运动,即满足(3.4)式,由Ito公式有
(3.1)
比较(2.2)式和(3.1)式可知两式均有相同的风险来源项dWt,如果假定资本市场无摩擦,存在连续的无风险利率r,期限结构水平,并且不存在相应的无风险套利机会,则可以通过对冲的方法消去风险,具体操作为:
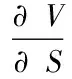
(3.2)
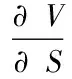
(3.3)
将(4.1)带入(4.3)中有
(3.4)
如果没有无风险套利机会,则在相应的无风险利率下应有
dΠ=rΠdt
(3.5)
整理有对可转债定价的B-S方程:

(3.6)
为了基于(3.6)式推导出可转债的定价公式,需要进一步做出如下相应的假设:
(1)为了分析问题方便,假设公司发行的可转换债券为零息债券,相应的面值为M。
(2)可转换债券的转股价格为K2,转股价格不变。
(3)对于回售条款,假定当股票价格向下触及K1时,投资者会向发行公司要求以面值M回售,即此时投资者的收益为V=M。

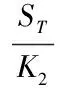
基于以上五点假设,相应的条款触发条件和投资者的收益可以视为可转债定价B-S方程的初边值条件,可转换债券的价值V可以通过如下系统加以描述:

(3.7)
通过求解该系统可以得到可转债的理论价值(具体的推导过程见附录):
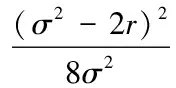

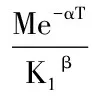
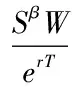

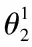
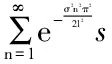
数学上可以证明,上述级数形式的解是收敛的,但是难以通过该式直接计算可转换债券的价值,并且零息债券的假设与市场的实际情形还有出入。虽然对该模型直接进行实证检验的意义不大,但是可以通过数值求解PDE(3.7),并同第三章的讨论,以一个算例对可转债价值的性质做相应的讨论。
基于有限差分法的古典显示格式可以数值求解方程(3.7)。算例的相关参数和说明如下:
回售条款的触发价格为K2=2,赎回条款的触发价格为K3=3.5,转股价格K2依次取2.2、2.4、2.6、2.8和3,无风险利率为0.03(按连续复利计算),波动率σ=0.1,债券面值为100,债券的期限为2年。当转股价格为2.8时,方程(3.7)的解如下图所示:
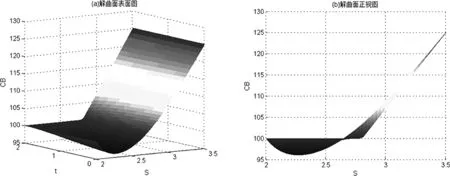
图3-1 方程(3.7)数值算例图示解
比较以上数值算例图示解的两个子图可以发现,可转换债券在各时点的价值属性与其在到期日的价值属性在趋势上是相同的,可转换债券在存续期内的价值变化是一个随时间向其到期日价值属性逼近的过程。
相应的可转换债券的价格与股价和转股价格的关系可以由下图进行说明:
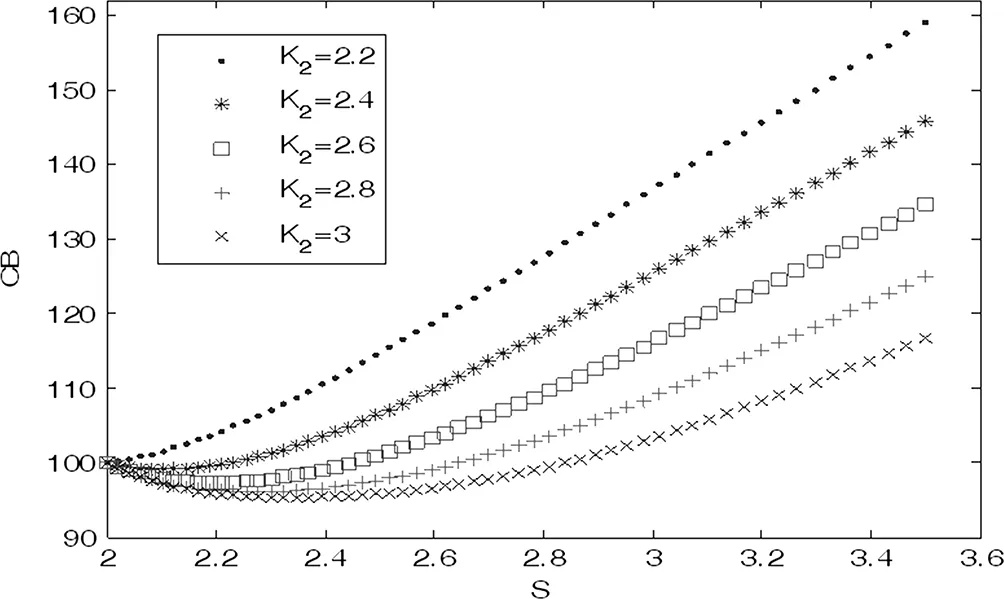
图3-2 不同转股价格下可转债价格与股票价格的关系
由上图可知,整体上来看,可转债的价格随股票价格的增加而增加,并且同样的初始股票价格下,转股价格越低,可转债的价格越高。虽然在股票价格处于较低的水平时,可转债的价格较之于面值会有所回落,但这种情形存在的区间很小,并且会随着转股价格的降低而逐渐消失。
(二)只引入可赎回条款的可转债定价
第一部分的讨论中虽然同时引入了赎回与回售条款,但是相应的关于可转换债券是零息债券的假定并不符合中国可转换债券市场的现实,并且最终给出的级数形式的解不仅形式上不够简洁,而且需要通过数值计算实现,不能根据市场上可转换债券相关股票的任意价格进行定价,精度上难以保证。然而在数学上,对于形如(4.7)式的有限区间上的抛物方程的混合问题,其形式上一般只有级数解,若要得到解析闭形式的解只允许有一个边界限制条件。
事实上,通过分析比较国内市场上流通的可转债可以发现,绝大部分可转债在存续期内都没有回售交易,并且我国对于发行公司发行可转债有着比较严格的审核和监管机制,能够发行可转债的公司的股票价格向下触及投资者要求的回售条件的可能性较小。基于以上两点原因,在我国的市场现实条件下可以不考虑引入回售条款,从而简化第一部分的模型,得到只考虑可赎回条款的可转债定价公式。
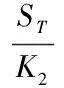

由数学物理方程相应的理论,类似于第一部分的替换,可将该系统等价转换为以下系统:
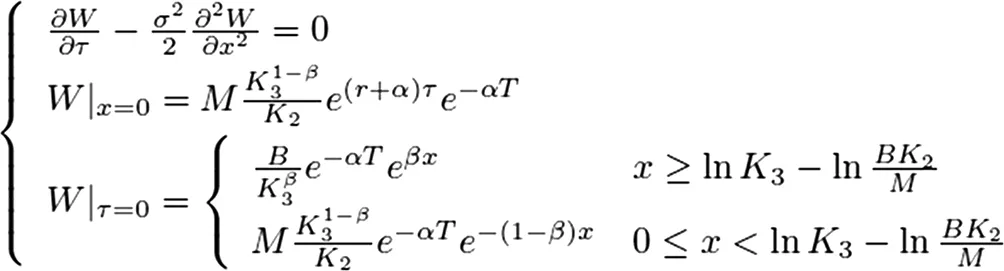

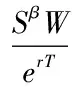
其中,
W=W1+W2+W3
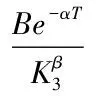

N(u)表示标准正态分布变量累计概率分布函数。
α,β同4.1节的讨论,参数z1,z2,z3,z4;d1,d2,d3,d4,d5,d6分别为:
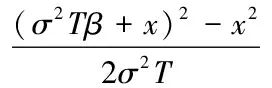



五、结语
可转换债券的定价研究在金融学、金融工程以及应用数学领域的研究都是一个十分具有意义的研究课题,不同的学者从不同的专业背景出发在可转债定价的研究中提出了许多经典的模型。其中,得益于金融工程等学科的发展,可转债定价的现代研究是在期权定价模型的基础上,借助相应的数学工具进行分析的框架下进行的,因此本文的整体研究思想是基于B-S期权模型的分析方法和无风险套利的思想对可转债的定价进行研究的,具体来说,本文的主要结论可以概括为以下几个方面:
第一,基于B-S欧式期权模型,将可转换债券中债券持有人的转股或有权益在一定的假设条件下视为欧式期权;考虑发行公司的违约风险,以发行公司持有的对相关股票价格的看跌期权来刻画违约风险的价值,基于B-S定价模型得出可转债的定价公式为:

第二,在可转债的定价研究中引入赎回与回售条款,给出了可转债理论价值的解析公式,并基于数值算例讨论了可转债价值的特性和变化过程;在此基础上,结合中国可转债市场的现实放松假定,即只考虑可转债中的赎回条款,通过求解带有初边值条件的B-S方程对可转债进行定价。
本文的整体研究是在期权定价模型的B-S方法下进行的,这种处理一方面为本文许多结论的推导带来了方便,另一方面却也导致了相应的结果与现实情形的差异。虽然可以通过一些假设将影响可转换债券价值的相应条款纳入模型中,但是可以通过前面的讨论看到,这样会增加模型数学求解的难度和结果的复杂性,虽然可以借助计算机编程实现,但也很难做到与现实完全的一致性。因此在考虑更复杂,或者说更加接近现实的可转债定价模型时,仿真模拟较之于解析求解,在保证仿真实验次数的条件下,其与现实的接近程度会更好。后续的研究可以相应的调整赎回条款的触发条件,进一步探讨这种赎回触发条件的调整对可转债价值的影响,得到更为深刻的结论。
[1]Black.F.M.Scholes.The pricing of Options and Corporate Liabilities[J].Journal of Political Economy,1973,5:637-654.
[2]Merton,R.On the pricing of Corporate Debt:the Risk Structure of Interest Rates[J].Journal of Finance,1974,29:449-470.
[3]张志强.期权理论与公司理财[M].北京:华夏出版社,2000.1.
[4]周鹏.信用违约互换定价分析[D].上海:同济大学,2007.
[5]姜礼尚,徐承龙,任学敏,李少华.金融衍生产品定价的数学模型与案例分析[M].北京:高等教育出版社,2008,6:267-273.
[6]Ingersoll J.A contingent valuation of Convertible Securities[J].Journal of Financial Economic,1977,4:289-322.
[7]Ingersoll J.A Examination of Corporate Call Policies on Convertible Securities[J].Journal of Finance,1977,32:463-478.
[8]Brennan M.J.Schwartz E.S.Convertible Bonds:Valuation and Optimal Strategies for call and conversion[J].Finance,1977,32:1699-1715.
[9]McConnel J.LynoTiming[J].Journal of Finance,1986,41(3):561-576.
[10]Lewis.C.M.Convertible Debt:Valuation and Conversion in Complex Capital Structures[J].Journal of Banking and Finance,1991,15:665-682.
[11]Song Ping,Jing Zhao.How should a convertible bond be Decomposed[J].Decision Econ Finance,2012,35(6):113-149.
[12]Tsiveriots.K.Fernandes C.Valuing Convertible bonds with Credit Risk[J].Journal of Fixed Income.1998,8(3):95-102.
[13]Bossaerts.P.Simulation Estimators of Optimal Early Exercise.Working Paper,1989,Carnegie Mellon University.
[14]杨如意,魏刚,刘孝红,孟辉.可转换债券及其绩效评价[M].北京:中国人民大学出版社,2002.
[15]郑振龙,林海.可转换债券发行公司的最优决策.http://efinance.net(2003)
[16]郑振龙,林海.中国可转换债券定价研究[J].厦门大学学报(哲学社会科学版),2004,(2):93-99.
[17]范辛亭,方兆本.随机利率条件下可转换债券定价模型的经验检验[J].中国管理科学,2001,9(6):7-14.
[18]范辛亭,方兆本.一种随机利率条件下可转换债券定价的离散时间方法[J].系统工程理论与实践,2002,(8):29-40.
陈垚翰(1992-),男,汉族,安徽合肥人,经济学硕士,武汉大学经济与管理学院,研究方向:西方经济学。
